Ding-投射模和粘合

张豫冈, 曹天涯

(1. 兰州工业学院 基础学科部, 兰州 730050; 2. 西北师范大学 计算机科学与工程学院, 兰州 730070)

文献[1]给出了三角范畴粘合的公理化定义, 其提供了将三角范畴分解为两个三角子范畴, 又将两个三角子范畴粘合成一个三角范畴的构造方法. 目前, Abel范畴和三角范畴的粘合已成为数学研究的基本工具, 在奇异空间、 代数表示论、 环论、 多项式函子理论等领域具有重要作用. 文献[2]给出了三角范畴稳定t-结构的概念, 三角范畴的粘合和稳定t-结构有密切的联系; 文献[3]提出了强Gorenstein-平坦模和Gorenstein FP-内射模的概念; 文献[4]称强Gorenstein-平坦模和Gorenstein FP-内射模分别为Ding-投射模和Ding-内射模, 同时利用Ding-模把Quillen模型结构下的同伦范畴从Gorenstein环推广到Ding-Chen环上; 文献[5-9]给出了关于Ding模以及粘合的相关结果. 本文在文献[6]的基础上继续研究Ding-投射模上的相关同伦范畴, 并且构造粘合及相应的稳定t-结构.

1 预备知识

设R是具有单位元的环, 本文所涉及的模均为左R-模, 复形均为上链复形.

定义1[4]若存在一个正合序列

P·=…→P-1→P0→P1→P2→…,

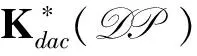
定义2[1]设D, D′,D″是三角范畴, D允许有关于D′和D″的粘合, 记作

(1)

其是指式(1)中6个三角函子满足下列条件:

1) (i*,i*),(i!,i!),(j!,j!)和(j*,j*)是伴随对;

2)i*,j!,j*是满嵌入函子;

3)j*i*=0;

4) 对D中的任意对象X, 可确定D中的两个三角:

i*i!X→X→j*j!X→i*i!X[1],

j!j*X→X→i!i*X→j!j*X[1].

如果4个正合函子i*,i!,j*,j*满足粘合定义中的相应条件, 则称三角范畴D允许有关于三角范畴D′和D″的右的粘合.

类似地, 可定义左粘合.

定义3[2]设U和V是三角范畴D的全子范畴, 用[1]表示三角范畴中的平移函子.如果其满足下列条件:

1) U=U[1], V=V [1];

2) 对于任意的X∈U,Y∈V, 均有HomD(X,Y)=0;

3) 对于D中的任意一个对象X, 存在三角A→X→B→A[1], 其中A∈U,B∈V.

则称(U,V)是D上的稳定t-结构.

2 主要结果

对于*∈{∞,-,+}, 定义K*(DP)的三角子范畴如下:

K*,db(DP)∶={X∈K*(DP)|对任意D∈DP, 均存在-m,k∈,

使得Hi(HomR(D,X))=0,i<-m,i>k}.

显然,Kb(DP),K-,db(DP),K+,db(DP)都是K∞,db(DP)的三角子范畴,Kb(DP)是K-,db(DP)和K+,db(DP)的三角子范畴.同理, 对于Ding-内射模的同伦范畴K*,db(DI), 可相应地定义三角子范畴Kb(DI),K-,db(DI),K+,db(DI).如果C是三角范畴D的三角子范畴并且关于直和项封闭, 则称C是三角范畴D的一个厚子范畴.上面涉及的三角子范畴都是厚子范畴.

引理1[2,10]1) 设C是三角范畴D的一个厚子范畴, 若典范嵌入i*: C→D有一个右伴随i!: D→C, 则存在下列右粘合:

2) 设(U,V)和(V,W)是D中的两个稳定t-结构, 则对于典范嵌入i*: V→D, 存在如下粘合:

并且Imj!=U, Imj*=W.

定义4若对R上任意正合序列

其中每个Di(i≥0)都是Ding-投射模, 则有Kerdn∈DP, 此时称环R具有性质(*).

引理2[6]设R是具有性质(*)的环, 则下列结论成立:

1) (K-,db(DP),Kdac(DP))是K∞,db(DP)中的一个稳定t-结构;

2) 典范嵌入i*:K-,db(DP)→K∞,db(DP)诱导出右粘合

引理3[2]设D是三角范畴, C是D的厚子范畴,q: D→D/C是商函子.则对于D中的稳定t-结构(U,V), 下列叙述等价:

1) (q(U),q(V ))是D/C中的稳定t-结构;

2) (U∩C,V∩C)是C中的稳定t-结构.

特别地, 假设C是U(或者V)的一个三角子范畴, 则V(或者U)可视为D/C的三角子范畴.此时, (U/C,V)(或者(U,V/C))是D/C中的稳定t-结构.

命题1设R是任意环, 则(K+,db(DP)/Kb(DP),K-,db(DP)/Kb(DP))构成了三角范畴K∞,db(DP)/Kb(DP)中的稳定t-结构.

证明: 首先, 有

HomK∞,db(DP)/Kb(DP)(K+,db(DP)/Kb(DP),K-,db(DP)/Kb(DP))=0,

对于任意X∈K∞,db(DP), 都有短正合序列

因为该序列是可裂的, 所以其诱导出了同伦范畴的三角：

显然,X≥1∈K+,db(DP),X≤0∈K-,db(DP), 结论成立.

定理1设环R相对于DP具有性质(*), 则下列结论成立:

1) (K+,db(DP)/Kb(DP),K-,db(DP)/Kb(DP)),(K-,db(DP)/Kb(DP),Kdac(DP))是K∞,db(DP)/Kb(DP)中的稳定t-结构;

2) 典范嵌入i*:K-,db(DP)/Kb(DP)→K∞,db(DP)/Kb(DP)诱导出粘合

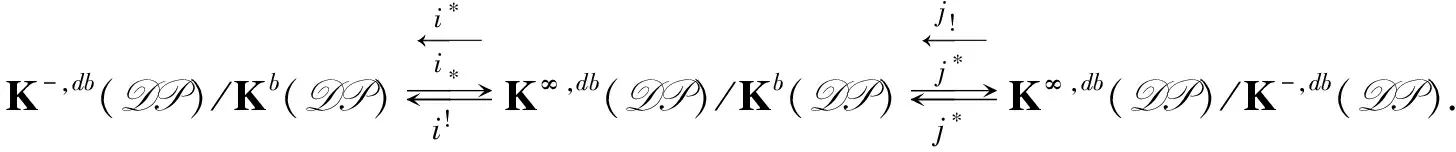
(2)

并且Imj!=K+,db(DP)/Kb(DP), Imj*=Kdac(DP).

证明: 由命题1知, (K+,db(DP)/Kb(DP),K-,db(DP)/Kb(DP))构成三角范畴K∞,db(DP)/Kb(DP)中的稳定t-结构.由引理2知, (K-,db(DP),Kdac(DP))是K∞,db(DP)中的稳定t-结构.因为Kb(DP)是K-,db(DP) 的三角子范畴, 所以由引理3知, (K-,db(DP)/Kb(DP),Kdac(DP))是K∞,db(DP)/Kb(DP)中的稳定t-结构.

由引理1中稳定t-结构和粘合的关系可得式(2)中的粘合, 并且易得Imj!=K+,db(DP)/Kb(DP),Imj*=Kdac(DP).

对偶地, 相对于Ding-内射模可得如下结论.

定义5若对R上任意正合序列

其中每个Di(i≤1)都是Ding-内射模, 则有Imd0∈DI, 此时称环R具有性质(#).

命题2设环R具有性质(#), 则下列结论成立:

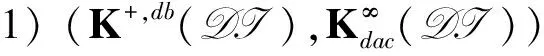
命题3设环R具有性质(#), 则下列结论成立:

2) 典范嵌入i*:K+,db(DI)/Kb(DI)→K∞,db(DI)/Kb(DI)诱导出粘合: