一类带时滞的Holling II 型功能反应的随机捕食系统的稳定性

郗丽莎 罗 东

（1、西安财经大学行知学院 通识部，陕西 西安710038 2、陕西服装工程学院 基础部，陕西 咸阳712046）

生物数学是生物与数学结合的一门交叉学科，并在发展和应用中建立和完善了自己的一套理论体系。它是通过构建数学模型的思想建立了生物种群模型，以此来研究生物种群之间的相互作用关系。然而生物种群之间的关系错综复杂但又非常重要，是我们研究生态学发展必不可少的一个环节。它们之间充满着相互捕食、竞争、依存和寄生等关系，捕食关系就是其中重要的关系之一，也是研究比较广泛、经验比较丰富的。那么在捕食系统中，庇护效应、年龄阶段、时滞效应，功能反应等都值得深入研究。我们本文重点研究的是时滞效应对系统的影响，考虑到生物种群密度的改变对增长率的影响存在时间滞后，比如，食饵与捕食者的妊娠期、哺乳期等。从而在对具有时滞等现实因素的系统进行研究时，主要讨论系统是否处于稳定状态并给出证明。因此时间滞后效应与种群系统的生存发展的状态息息相关。更全面的了解种群的生存发展状况，是目前许多学者关注的问题之一。

但是，在生物界中，无论大小生物都或多或少的受到内在或外在因素的影响。比如内在因素有：种内竞争、生老病死、迁入或者迁出以及性别比例不均衡等。外在因素有：人类对于动物的猎杀、或者保护的行为、大自然的气候、动物入侵，食物供应等。有利条件下生物的种群密度增大，不利条件下生物的种群密度下降。比如：阳光充足、雨水充沛，植物就会枝繁叶茂，食草动物就会粮食富足，物种数量就会随之增加；否则，就会减少。所以，为了更全面的了解生态系统的发展状态，我们在以往的确定性模型中加入随机因素得到随机系统模型，以此来分析种群的性态。终于在各位学者的不断努力、大胆尝试中总结收获了现有的宝贵经验和有效方法。在文献[1-4]中，作者们主要研究了在随机因素的干扰下的具有时滞因素的Lotka-Volterra 模型，分析其解具有的特殊性质，从而得到模型符合的生物学特性。其中文献[3]和[4]都分析了具有时滞的随机Lotka-Volterra 模型，前者加入了可变时滞，后者加入了无限时滞，分别讨论得到其解的全局渐进稳定性。文献[5,6]研究了随机时滞Logistic 系统模型的持久性和灭绝性。文献[8]和[11]分析了具有时滞和随机项的捕食系统，得到解的一系列特性。文献[9]讨论了具有时滞和扩散效应的随机捕食系统模型，得到系统全局正解存在并且唯一，以及当系统灭绝或者平稳生存时解所满足的条件。本文将研究具有时滞的HollingII 型的随机捕食系统，对于确定性捕食系统表示如下：

考虑随机因素的干扰，研究捕食者具有时滞的Holling II 型功能反应的捕食系统，对上述确定性系统做变换a→a+σ（1x（t）-x*t），-d→-d+σ（2y（t）-y）*（t），得到如下随机系统：

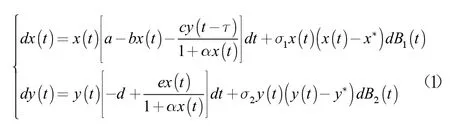
方程中，x（t），y（t）分别指t 时间，被捕食者的种群的数量，捕食者种群的数量，x*，y*为不含随机干扰时系统的正平衡点，a，b，c，d，e，α 均为常数，α 表示被捕食者在不受外界干扰下自身的一个增长比率，b 表示被捕食者的种内之间的一种竞争制约常数，c，e 分别是指被捕食者和捕食者这两个种群之间的约束比率，d 表示捕食者的一个自然死亡比率。

τ 表示时间滞后效应，表示在这一时刻之前，对于捕食者而言，才具有能够捕猎和觅食的能力。

1 系统正解的存在唯一性

证明t≥0时，设初值函数u（0）=lnx0，v（0）=lny0，得到方程

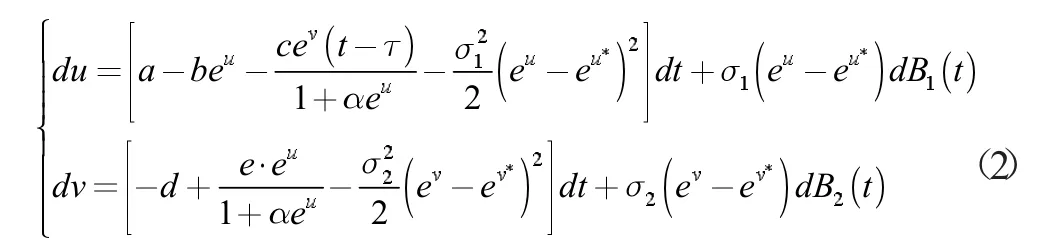
定理1 对任意给定初值（x0，y）0∈R，系统（1）具有唯一解(x(t) ,y(t)),t≥0, 并且此解依概率1 停留在R中。

证明 由引理1，只需要证明τe=∞，a.s.即可。

设n0＞0 足够大，使（x0，y0）的每一个分量都落在[1/n0，n0]中，定义停时τk=inf {t∈[ 0 , τe) :x(t) ∉( 1 /n,n)或y(t) ∉(1 /n,n)},其中。令 inf∅=∞，显然，当n→∞时，τk单调递增，令则 τ∞≤τe,a.s.。若能证明τ∞=∞，a.s.，则τe=∞，a.s.. 也就证明了 (x(t) ,y(t)) ∈. 即，对于该定理只需要证明 τ∞= ∞,a.s.。假设存在常数T＞0 和ε∈（0，1），使P＞ε，则存在当时有

定义一个C2函数V：R→R+，V（x，y）=（x-1-lnx）+（y-1-lny），由于当u＞0 时，u-1-lnu≥0，因此V（x，y）是一个非负函数。

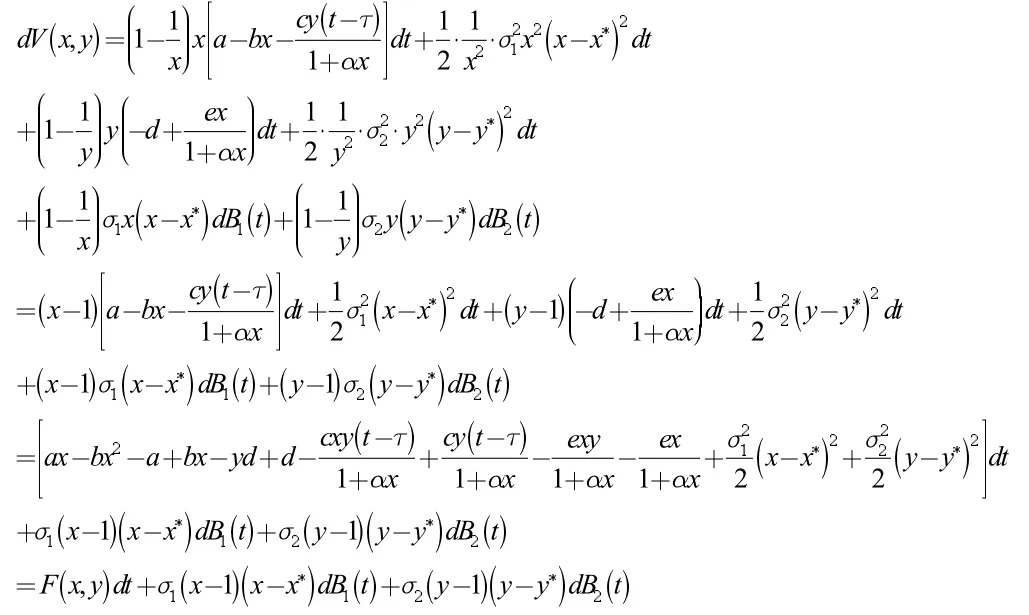
其中

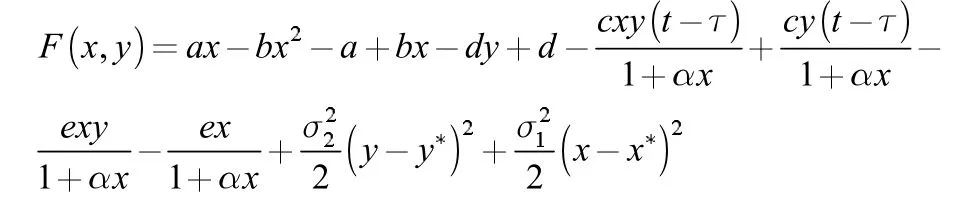
则有

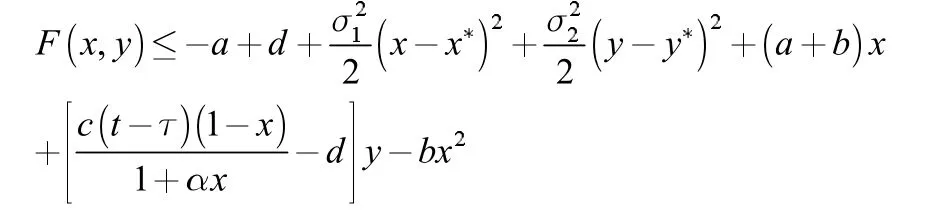
显然F（x，y）有上界，设其上界为K＞0 则

2 解的随机最终有界性

定义1 模型（1）的解是随机最终有界的，若有对所有的ε∈（0，1）只要有大于0 的数δ=δ（ε）＞0 使得对所有的初始解（x0，y）0∈R模型（1）的解符合以下条件：

引理2 对所有的θ∈（0，1）只要有大于0 的数H=H（θ）和初始解（x0，y0）∈R2+无关，使得模型（1）的解（x（t），y（t））符合以下条件：

3 解的全局随机渐近稳定性

定理3 如果A＜0，4AB-C2＞0 且e（1+αx*）-c（t-τ）＞0 则系统（1）的正平衡点（x*，y*）是全局随机渐近稳定的。

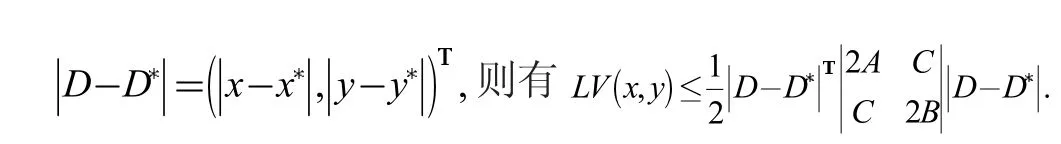
所以，若A＜0，4AB-C2＞0，满足e-αd＞0，0＜m＜1-bd/[α（e-αd）]成立，则LV（x，y）＜0。 因此沿着第一象限中除了（x*，y*）以外的任何轨线的正向都有LV（x，y）＜0 成立。

因此，考虑到时间滞后的影响构建HollingII 型功能反应模型，深入探讨该模型在噪声干扰作用下的系统种群是否趋于稳定，若时间滞后效应影响较小时，即e（1+αx*）-c（t-τ）＞0 时系统处于全局稳定状态，对保护生物多样性以及维持生态平衡起着重要作用。