基于无标度先验的有向无环图结构学习

苏温庆, 郭 骁, 张 海

(西北大学数学学院，西安 710127)

0 引言

复杂网络是近年来医学、计算机科学和统计学等领域研究的热点问题之一。Albert 和Barab´asi[1]研究发现，不同于随机网络，在基因网络、社交网络和社会网络等大多数真实网络中，网络节点的度服从幂律分布，即网络中节点的度为d的概率正比于d−γ，这里γ> 0。这类网络称为无标度网络。无标度网络的典型特征是网络中存在少数中心点(hubs)拥有极其多的边连接，而大多数节点只有很少量的边连接。在实际中，少数中心点往往对无标度网络起着主导作用。因此，在无标度的假设下研究网络的结构，从而理解真实网络的功能和特征不仅具有理论意义，更具有实际价值。

图模型[2]作为一种分析网络结构的方法被广泛使用。图模型的基本思想在于通过图表示随机变量联合分布，并基于分布研究变量之间相互关系。图中的节点表示随机变量，边度量随机变量间的关系。根据边是否有方向，图模型可分为有向图模型与无向图模型。本文基于有向图模型开展真实网络结构分析。有向图模型可度量随机变量间的因果关系，两变量间的箭头Xi →Xj表示Xi是Xj的直接原因。因果关系在生物科学、医药学和人工智能等领域广泛存在。因此，研究有向图模型具有重要意义。有向无环图(Directed Acyclic Graphs, DAGs)是指边有向，但不存在有向环的图，作为有向图模型的一个特类，近年来受到广泛关注。相比于无向图模型，DAGs 的估计是一个困难的问题，主要难点在于DAGs 的结构学习往往对应于一个NP 难问题，且由于观测等价性，可能无法估计边的方向。大多数现有估计DAGs 的方法可大致归为两类。第一类是基于约束的方法。Spirtes 等[3]提出的PC 算法和Tsamardinos 等[4]提出的MMHC 算法均为此类方法。这类方法通过一系列条件独立性的检测来判断节点之间是否存在边，主要缺点在于实际问题往往难以满足上述方法的假设。第二类是基于准则的方法，即通过最优化给定的评分函数来估计DAGs。Lam 和Bacchus[5]通过最小描述长度构造评分函数，Heckerman 等[6]通过贝叶斯方法来估计DAGs。网络的一个主要特征在于实际中存在大量稀疏网络，所谓稀疏网络是指网络中存在的边是稀疏的。因此，目前发展起来的稀疏正则化方法越来越多的被应用于网络结构学习建模。Shaojaie 和Michailidis[7]在假定节点序已知的条件下，提出通过罚对数似然估计方法直接估计高斯DAGs 的邻接矩阵。Fu 和Zhou[8]在假定节点序未知的条件下，通过l1正则化方法研究稀疏DAGs 的结构学习。随后，Aragam 和Zhou[9]将该方法进一步推广到非凸惩罚下。文献[10]分析了高斯分布下高维稀疏DAGs 的l0惩罚估计的理论性质。

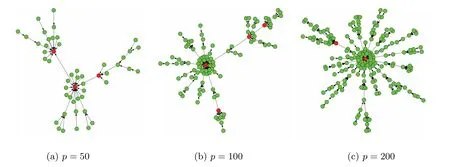
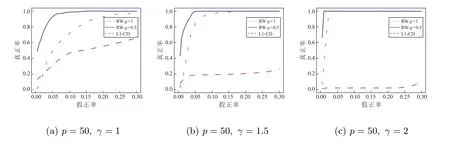
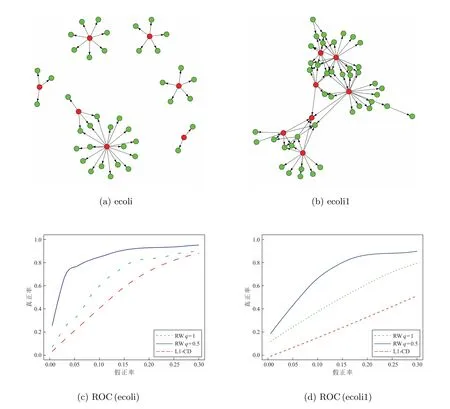
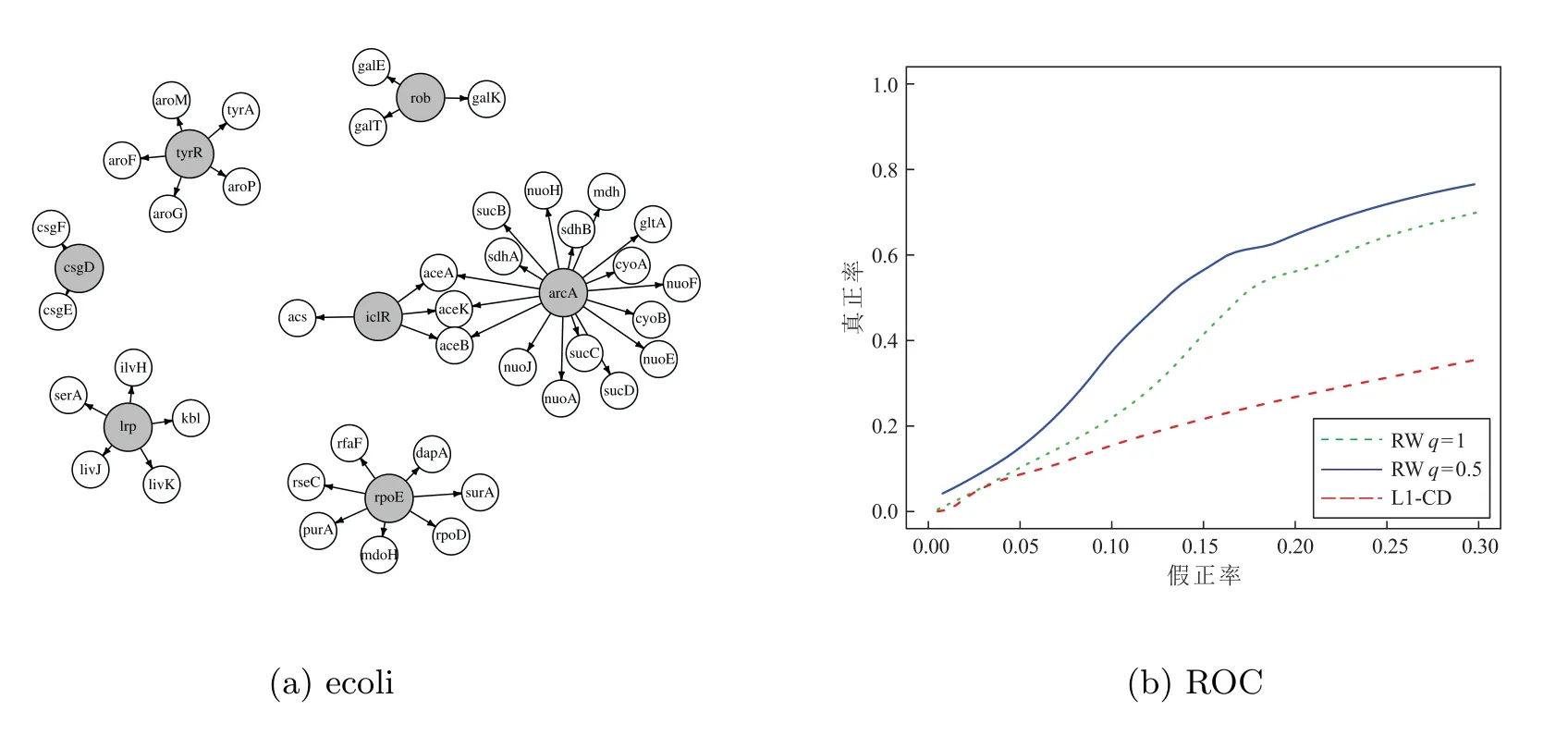
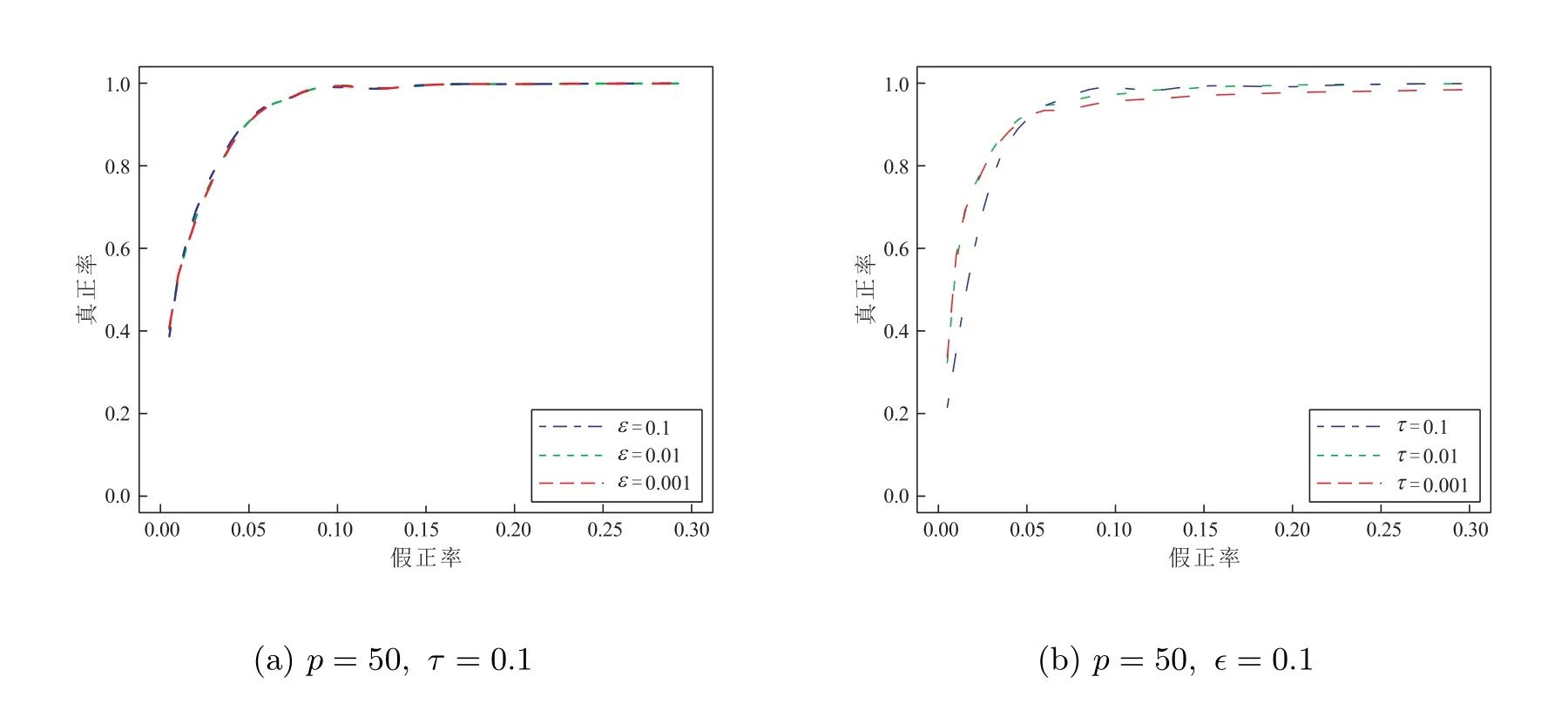
上述正则化方法大多通过l1型惩罚函数来引入稀疏先验。但l1型罚项并不能反映网络的无标度特征。近来，部分学者通过引入无标度先验，对无向图的结构学习开展研究。Liu 和Ihler[11]直接利用网络节点的度服从幂律分布这一先验信息，提出了罚项为Log 型与l1型惩罚函数复合的模型，用l1范数近似节点的度，并提出用重赋权迭代算法来求解这一模型。进一步，Guo 等[12]用lq(0

本文在假定节点序已知的条件下，研究具有无标度特征DAGs 的结构学习问题。通过引入网络中节点度的信息和边的稀疏先验，构造罚项为Log 型与lq(0

1 有向无环图结构学习模型

本节讨论具有无标度特征的稀疏有向无环图结构学习模型。首先我们给出有向无环图模型的数学表示，然后基于无标度信息，构建新的稀疏有向无环图结构学习模型。

有向无环图是图中只包含有向边，不包含有向环的一类图。考虑一个DAG，G=(V,E)，这里V= 1,2,··· ,p对应于图的p个节点，且节点j(j= 1,2,··· ,p)表示随机变量Xj，E ⊆V×V代表有向边。边(i,j)∈E可表示为i →j。此时节点i称为节点j的父代节点，记为i ∈pa(j)。在本文中，我们主要关注高斯有向无环图模型。DAGs 的p个节点对应的随机变量Xi,··· ,Xp，服从均值为0，方差为Σ0的p维高斯分布，即Xi,··· ,Xp ∼N(0,Σ0)。

我们称(B0,Ω0)是对应于Σ0的DAG。对于一个DAG 对应的邻接矩阵，由于图中不存在有向环，因此，可通过置换把邻接矩阵变为下三角矩阵。在本文中，我们关注节点序已知的情形，因此，同样可通过提前置换把B0变为主对角线元素为0 的下三角矩阵。不失一般性，我们以下假定B0为下三角矩阵。

其中λ> 0 是调控参数，该参数中包含了尺度参数γ。显然，该模型可划分为p个独立的子模型，其中第j个子模型对应B的第j列。

注1 在模型中添加大于零的常数ϵ以保证log 函数有意义。求解过程中可将ϵ视为调整参数，以得到模型的全局最优解或局部最优解，但通过实验发现该方法对ϵ不敏感。因此，本文预先设定ϵ为一个较小的常数。

2 算法及其收敛性分析

1: 令k =0，输入τ >0, ϵ>0 及初始值βt(0)j =βtj。2: 对于k =0,1,2,···，重复下式直至收敛或达到要求的迭代次数βt(k+1)j =arg min βj Rτ(βj;βt j,βt(k)j )=arg min p∑1//Xj −Xβj//2 2+λ2ωt j2 q βj i=1//βtj//qq+ϵ(βt(k)ij +τ)1−q|βij|.

3: 令βt+1 j 等于步2 输出结果。

3 实验

本节通过数值模拟和实际数据来说明我们方法有效性。在模型(6)中，考虑到lq(0

数值实验中数据的生成方式如下。首先，我们用Albert 和Barab´asi[1]提出的择优连接机制来生成具有无标度特征的有向无环网络。具体地，给定一个初始节点，对下一个新的节点，以正比于的概率选择某个已有节点，并生成由新节点指向旧节点的边，这里di为已有节点i的入度，γ为尺度参数。其次，对于邻接矩阵B，若节点i是节点j的父代节点，则令βij为大于0 的常数β，否则令βij为0。对于协方差矩阵Ω，数值实验中令ωj为1。最后，通过线性结构方程模型(2)来生产实验数据X。

我们通过ROC 曲线来度量各方法的优劣。该曲线反应了调控参数λ变化时各方法估计真实网络的整体表现。ROC 曲线的横轴是FPR(False Positive Rate)，纵轴是TPR(True Positive Rate)，这里FPR=FP/(FP+TN), TPR=TP/(TP+FN)，其中TP(True Positive)为真实网络有边，模型估计为有边的个数；FP(False Positive)为真实网络无边，模型估计为有边的个数；FN(False Negative)为真实网络有边，模型估计为无边的个数；TN(True Negative)为真实网络无边，模型估计为无边的个数。

实验1 我们分别比较网络维度p，信号强度β，尺度参数γ不同时三种方法的表现。首先，给定尺度参数γ= 1，生成维度分别为p= 50,100,200 的网络，图1 为具体网络。在不同网络维度下，分别比较信号强度为β=2,1,0.3 时各方法表现。这里样本大小固定为n=100，ϵ和τ均固定为0.1。图2 为实验结果。其次，讨论当网络中hubs 的影响增大，即γ变大时三种方法的表现。给定网络维度p= 50，样本大小n= 100，信号强度β=1，ϵ和τ均固定为0.1，分别给定γ=1,1.5,2，图3 为实验结果。每条ROC 曲线均为重复20 次实验结果(以下数值实验均为重复20 次结果)。其中，RWq=0.5 表示本文提出的模型，我们选择q= 0.5 为本文模型的代表。RWq= 1 表示罚项为Log 型与l1型惩罚函数的复合模型，通过重赋权迭代算法求解。L1-CD 表示Shojaie 和Michailidis[7]提出的l1惩罚对数似然估计方法，通过坐标下降算法求解。

图1 实验生成有向网络，维度分别为50、100、200

从图2 可以看出，几乎在所有情况下，本文方法RWq= 0.5 的表现好于其它两种方法。当信号强度β固定而网络维度p变化时，随着维度增大，三种方法的表现基本上均逐渐变差。当p= 50 时，RWq= 1 的表现稍逊于RWq= 0.5，但随着维度增大，除β= 0.3 外，RWq= 1 的表现与RWq= 0.5 的差距逐渐变大。当信号强度低(β= 0.3)时，三种方法的表现均变差，此时本文方法的表现仍好于其它两种方法但优势不明显。从图3 可以看出，在不同尺度参数γ下，本文方法的表现均好于其它两种方法。随着γ增大，RWq= 0.5 和RWq= 1 的表现均变好，L1-CD 的表现变差。这说明本文方法对重建由中心节点主导的网络上是有效的。

图2 不同(p,β)下ROC 曲线

图3 不同尺度参数γ 下的ROC 曲线

实验2 实验1 中均通过择优连接机制来生成具有无标度特征的有向无环网络，且均为节点入度服从幂律分布的网络。为说明我们所提的模型对重构节点出度服从幂律分布的网络上仍有效，我们选取两个节点出度服从幂律的真实网络作为实验网络，并通过线性结构方程模型(2)生成实验数据X，即使用真实网络但不使用真实数据。第一个网络为大肠杆菌(escherichia coli, ecoli)转录调节网络，Kao 等[22]提出利用网络结构分析来推断大肠杆菌的转录调控网络。他们提供了7 个转录因子和40 个受调控基因的大肠杆菌调节网络，即网络维度为p= 47，见图4(a)。第二个网络为DREAM3(Dialogue on Reverse Engineering Assessment and Methods)数据集[23]中的ecoli1 网络，网络维度为p=50，见图4(b)。显然ecoli 网络中节点出度服从幂律分布，而ecoli1 网络中同时存在高入度的中心点和高出度的中心点。实验中给定样本大小n= 30，ϵ和τ均固定为0.1。图4(c)和图4(d)为对应ROC 曲线。本文方法的表现均好于其它两种方法。这说明本文方法在网络节点出度服从幂律分布时同样是有效的。

图4 实验网络和对应的ROC 曲线

实验3 我们通过真实数据验证所提方法的有效性。我们研究ecoli 网络，实验中使用Kao 等[22]提供的23 个时间点上7 个转录因子和40 个受调控基因的基因表达数据，即样本个数为23。图5(a)为已知网络(包含基因名称)。图5(b)为实验结果。可以看出本文方法的表现优于其它两种方法。这与数值实验中结果一致。

图5 ecoli 调节网络及三种方法的ROC 曲线

以上实验中我们固定ϵ和τ均为0.1。现在我们讨论ϵ和τ的取值对本文方法结果的影响。对于ϵ，给定实验网络为图1(a)，样本大小n=100，信号强度β=1, τ=0.1，分别给定ϵ= 0.1,0.01,0.001。对于τ，给定实验网络为图1(a)，样本大小n= 100，信号强度β= 1, ϵ= 0.1，分别给定τ= 0.1,0.01,0.001。图6 为实验结果。从图6 可以看出我们的方法对ϵ和τ的取值不敏感，因此预先固定ϵ和τ是合理的。

图6 不同ϵ 和τ 下的ROC 曲线

注4 考虑到运算效律，在实验中均采用一步重赋权迭代。实验表明一步重赋权迭代求解效果明显。

4 结论

本文研究在无标度先验下，节点序已知的有向无环图结构学习问题。通过引入网络中节点度的信息和边的稀疏先验，构造罚项为Log 型与lq(0