基于Monad的可认证数据结构

贺新征 光 焱 祝跃飞

1(中国人民解放军战略支援部队信息工程大学 河南 郑州 450001) 2(河南大学计算机与信息工程学院 河南 开封 475000)

0 引 言

可认证数据结构(Authenticated Data Structure)是基于Merkle[1]树的二叉树数据结构。用户从树上获得某个数据的同时，还得到从根到数据的路径信息，后者称为证明流。依靠证明流能校验所获得数据的真实性。例如，比特币的超级账本底层采用了Merkle树结构，经过实践测试能有效防止中间人攻击。Merkle树启发研究人员，按照链表、字典等方式组织的数据也可重新设计为基于Merkle树的可认证数据结构，但对每类非二叉树结构都需重新设计。

Miller等[2]从Merkle树中抽取出生成证明流和验证证明流的操作性语义，将两者写入编译器，然后作为一种新的程序设计语言特性提供给编程人员，从而能让非二叉树数据结构使用可认证数据结构进行数据验证。这种实验性的方法是在OCaml编译器上实现的。但不足之处是，研究人员在具体实施时需要掌握Hack OCaml和特定于OCaml编译器的Camlp4语法树转换技术，因此难以移植到其他编译器中实现。

本文采用一种更为抽象和凝练的基于范畴论的Monad技术，通过将编译器中一小部分操作性语义转化为等价的指示性语义，可从编译器中抽取出需要的语义将其转化为目标编译器语言编码的库文件供程序员调用。因为Monad适用于所有基于Hindley-Milner[3]类型推导系统函数式的编程语言，所以这种方法能推广到所有这类编程语言编译器。

1 背 景

1.1 研究背景

文献[2]首次提出将Merkle树证明语义写入到编译器的方法。文献[4]全面分析和总结了ADS算法。文献[5-6]从数字金融领域的实践角度，介绍了使用ADS的Merkle树创建区块链的技术细节。在类型理论和范畴理论的交叉领域，已经有很多学者对Monad理论和应用进行了深入的研究和讨论。文献[7]第一次从理论上通过范畴论的Monad将操作性语义等价翻译为指示性语义。文献[8-10]将Moggi的Monad理论逐步应用到了ML系列的函数式编程语言，范畴论因此正式成为OCaml和Haskell语言的重要理论基础。文献[11-12]对迄今为止的Monad概念的各种形式化和比喻性的解释进行了总结。文献[13-14]对以操作性语义为主的类型理论进行综合讲解，多数程序设计语言都是基于其中理论语言系统F或Fw进行二次开发。文献[15-17]分别从程序员角度、计算理论角度和范畴论专家角度对与Monad紧密相关的函子、自然转换和伴随函子进行了全面介绍。

1.2 Merkle树

Merkle是一个带有Hash指针的二叉树，如图1所示。叶子节点存储数据，非叶子节点存储Hash指针。先计算两个叶子节点存储的数据的哈希值，然后将结果存储到父节点。如此反复计算，直到计算根节点左右孩子的哈希值，并将结果存储到根节点中。Merkle树最主要的优点是能提供节点与Merkle树关系的证明。例如，如果客户向服务器提出数据d2的请求后，服务器向客户端返回〈data,proof〉。

proof=hash(h1,h2)+hash(h3,h4)+hash(d2)

path=〈L;R〉

如果客户希望知道数据d2是否确实是Merkle树的成员，可以从叶节点沿路径〈L;R〉计算每个中间节点的哈希值，向上一直到根节点，依次与证明流proof提供的哈希值进行比对。

图1 Merkle树沿着路径〈L;R〉生成数据d2的证明流proof

2 Monad理论框架和解释

来自范畴论的Monad是函数式编程语言中最抽象的概念之一。理论上的Monad概念是位于范畴论2-Category维度上，在编程语言的具体实践中隐藏在functor中。已发表的研究Monad的文献可分为面向纯理论研究人员、面向编程应用人员和面向理论应用结合人员三类。本节选择从理论与应用相结合的角度来引入Monad的解释。

2.1 计算的一般化

通常程序被认为是函数。但计算机科学中的程序，与数学中的函数有很大区别。给定相同输入，每次运行程序可能会得到不同结果。例如，数学上的函数f(x)=x+1作为计算机中的程序运行时，可能会有以下几类结果。

(1) 如果输入x=1，结果为2；如果程序在运行时，突然断电则结果未知，记为⊥。结果集合B=f(A)+⊥。其中，+号表示OR的关系。

(2) 如果输入x=1，结果为2；如果得到计算结果，将结果打印到屏幕上。结果集合C=(f(A),S)=f(A)×S。其中，×表示AND关系，S表示输出到屏幕。

以上两个例子说明，数学上的函数变为计算机上的程序后，即便每次输入固定数值，也可能会得到不同的输出结果集合。为表示区别，将数学上函数称为纯函数，将程序表示的函数称为非纯函数，这两类函数都有“计算”的概念。很容易看出绝大多数程序都是非纯函数的计算。若能将计算概念一般化，即用一种数学公式统一数学上的纯函数和程序的非纯函数的表示，则能将数学和程序通过一般性计算连接起来。计算一般化的典型代表是范畴理论中的Monad。

2.2 范畴和对象

因为注意到数学对象在映射时具有保留结构的特点，因此范畴论期望能抽象出数学结构映射关系。例如，将范畴论应用到编程语言的类型理论研究时，可将数据类型类比为对象，类型之间的映射类比为态射。函数f1:int→int，f2:char→char和f3:float→float都有相似的结构。果让所有简单数据类型从类型变量*={α,β,γ,…}中取值，那么上述三个函数具有统一的形式，即f:*→*。

2.3 函 子

定义2函子(Functor)

并且满足以下条件：

(2)F1(id(A))=id(F0(A))。

(3)F1(f∘g)=F1(f)∘F1(g)。

2.4 自然转换

定义3自然转换(Natural Transformation)

自然转换φ:F→G符合范畴论统一形式•→•，此时•表示的数学对象是函子。自然转换表示“(映射后的)结构1→(映射后的)结构2”的两个映射后结构之间的转换。如果将函子代入到自然转换中，会得到一个抽象关系“(原始结构→映射后的结构1)→(原始结构→映射后的结构2)”。

2.5 态射、函子和自然转换的比喻

2.6 纯函数组合需满足的属性

程序可由多个函数组成。程序的可组合性表示整个程序的行为由所构成的每个函数决定。假设，P=h∘g∘f构成一个程序，令P1=h∘g，P2=g∘f，那么P1∘f=h∘P2=P。表示的含义是程序P可像搭积木一样构成，先挑选功能f，再与功能P1组合的结果，与先挑选功能P2再与功能h组合的结果是一样的。因此，可组合的含义是功能可替换。在数学上纯函数满足可组合属性的集合M，就是含幺半群(monoid)代数结构(M,⊗,)。其中⊗表示某种组合操作，表示单位元。

值得注意的是，含幺半群是非对称代数结构，即没有属性g∘f≠f∘g。这种特性恰好满足编程时函数调用顺序的要求，即一个函数序列不同调用顺序生成不同结果。如果将数据当做对象，函数当做态射，程序非常像一种含幺半群代数结构。

2.7 非纯函数的组合性问题

任意程序都能当作函数，从两个已有函数可以组合出新函数。函数组合的要求是前一个函数的值域等于后一个函数的定义域。实际情况是，并非每个函数的输入都能恰好映射到函数的输出中，会产生一些附加行为或数据。例如，将数据写入文件，数据输出到屏幕。这类附加行为称之为计算效果(computation effective)，此类函数称为非纯函数。类比纯函数，非纯函数能够组合必须满足两个条件，一是要具备模拟纯函数的单位函数(identity function)，二是要具备自定义的两个函数的组合规则。

Moggi观察到所有非纯函数都有一样的称为Monad的计算结构。如果输入数据为A，将所有在此结构上函数操作的集合统称为T。那么输出结果要么就是TA，恰好是所有对应于输入为A的、纯函数集合为T的输出结果的集合。要么输出结果是TB，表示输出结果对应于所有输入为B的、所有纯函数集合为T的输出结果的集合(如图2所示)。如果比较TA与TB输出结果的大小，TB比TA多出来的数据结果是TB具备的而TA所没有的行为结果，就是所谓的计算效果。如果f:A→TB与g:B→TC进行组合，只需要将g的定义域B扩大为TB，同时将g的陪域扩大为TTB即可。因此，常有术语称Monad进行了两次扩展。准确的Monad数学定义见下节。

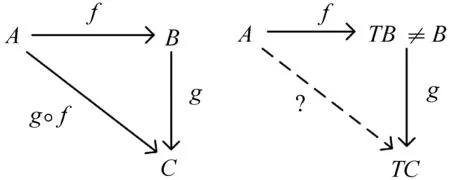
图2 如果TB≠B则无法组合函数

2.8 Monad的数学定义与解释

Monad有两种范畴论的解释性定义。需要指出，由于Monad是位于2-Category维度，所以试图绘制或想象出某个Monad内部结构是非常困难的事情。如果将Monad想象为一个球体，准确描述球体内部到底具体包含哪些态射和对象是非常困难的。但通过建立一套准则只测试球体外部所表现出行为，同样能间接确定球体内部所有成员的共同属性。

2.8.1两种Monad定义形式

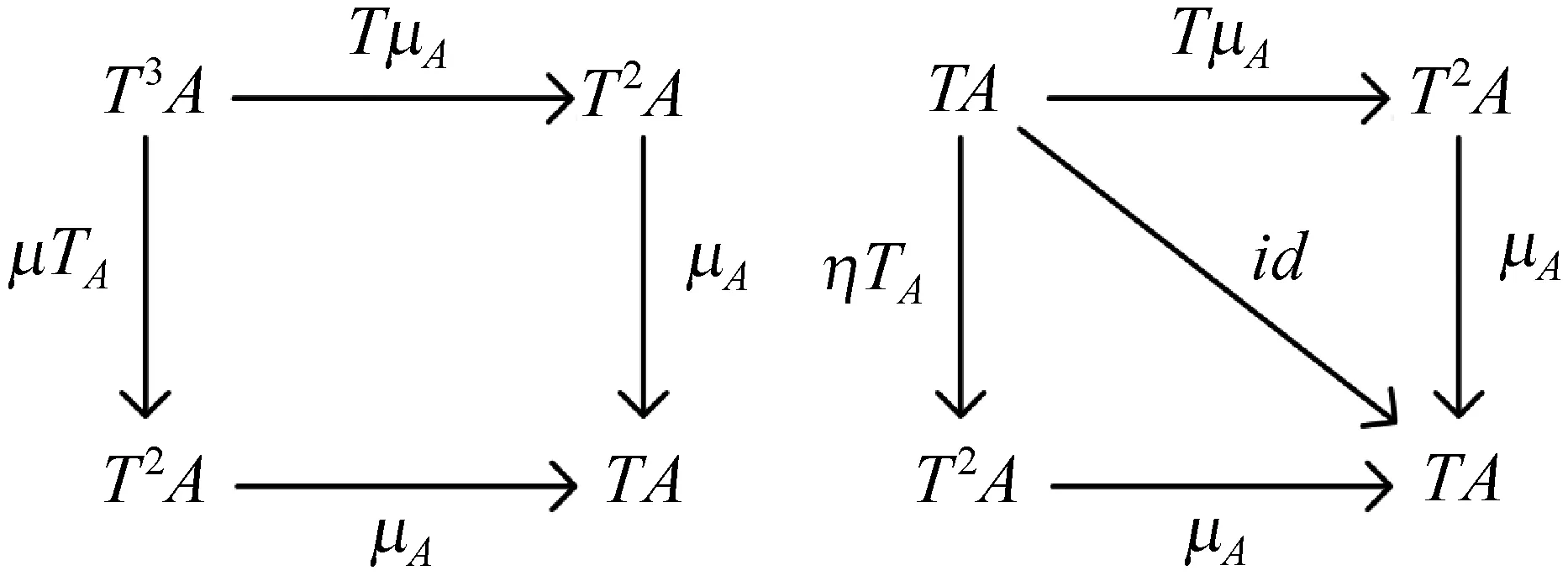
图3 Eilenberg-Moore解释的Monad含义

如果输入数据为A，则ηA:A→TA，μA:T2A→TA。对应到函数式编程语言中的monad，η就应为return(ret)操作，而μ对应为join操作。第一种解释便于理解Monad，但不便于具体编码实现，主要是因为join操作异于编程人员对函数组合的一般性理解。

非纯函数f:A→TB和g:B→TC内部是什么具体数学形式并不重要，重要的是前一个函数的值域与后一个函数的定义域相同。T是范畴论中的函子，表示计算，它可看作是把一种结构映射到另外一种结构的函数。Eilenberg-Moore的解决思路是：

(1) 先同时扩大g的定义域与值域，即T(g):T(B)→T(TC)。如果将T(g)简记为Tg，T(TC)记为T2C，则有Tg:TB→T2C。目的是保证前一个函数的值域与后一个函数的定义域相同。

(2) 由于扩充g后值域变为了T2C，因此需要通过自然转换μ让T2C变为TC，即μC:T2→TC。

图4 Kleisli条件满足的两个等式ηA=idTA和f*∘ ηA=f

(4) 如果存在f*:TA→TB，必定存在f:A→TB。是Keisli的扩展推论，常称为lift(f)操作，记为f*。f*就是函数式编程语言中Monad的bind(>>=)操作。

假设有函数f:A→TB和g:B→TC，Kleisli的定义下g*∘f*=(g*∘f)*。其中f*:A→B表示纯函数，f:A→TB表示非纯函数，f*:TA→TB表示lift就是函数式编程语言中的bind函数(如图5所示)。如果要计算g∘f就先要将f提升为f*，g提升为g*，因此实际计算的是g*∘f*。

图5 Klesili函数组合的解释

2.8.2Monad计算的解释

非纯函数的值域难以确切表示，因为不同计算方式会产生不同值域集合。一种较为容易理解的观点是，计算就是value-set形式，即输入一组数据集合生成结果集合。这种观点下，计算的结果是集合。但如果将计算理解为value-function的形式，即输入一组数据生成一种适合某种类型集合的计算，则计算的结果是另外某个计算。

例如，函数f(x,y)=x+y。当输入x=1时，结果是另外一个函数，即g(y)=f(1,y)=1+y，这是一种value-function的形式。由函数g(y)能产生结果集合，而一旦确定y的具体数值，结果必定在此集合中。因此，函数产生了结果集合，结果集合就能用函数表示。从这个角度来看，函数就是数据。

如图5所示，由于函数就是数据，因此生成的数据集合记为TB。如果B=A，生成的数据就是TA，表示A→TA。抽象出代数结构变为(1→T)(A)，其中(1→T)就是抽象代数结构，A表示输入的数据集合。丢掉具体的A，保留下的(1→T)就是•→•形式。因为T是函子，所以1→T必定是自然转换，命名为η:1→T。可看出η唯一做的事情是将A原样输出为TA。此时η类似于编程中经常需要的空操作，例如已经计算出函数结果，再计算一次仍旧是原结果。

对于生成数据操作T如果能组合，就应该满足类似于含幺半群的代数结构。前面已经找到单位操作η:1→T，类似必须还要有组合操作满足μ:T×T→T，简记为μ:T2→T。由于T是函子，所以μ必定是自然转换。考察其中的组合，μB:T2B→TB。结合上面分析就有，μB∘Tf∘ηA:A→TB，而因为f:A→TB，因此μB∘Tf∘ηA=f。

上述代数结构就是Monad，记为(T,η,μ)。与含幺半群(M,⊗,1)对比，两者都具有•→•的结构。对于含幺半群来说，•对象是集合，→是函数。对于Monad来说，•对象是函数表示的集合(即将计算当作对象)，而→则是从一种计算结构到另外一种计算结构的映射，即自然转换。Monoid的底层结构是集合，它可将纯函数组合；Monad通过一般化计算，将函数当做数据对待，可将非纯函数组合。因此，常称Monad是在自函子上的含幺半群代数结构，实现了一般性计算的函数组合操作。

2.9 操作性语义到指示语义的转换

文献[9-10,12,18]从纯编程角度解释Monad，而不涉及任何范畴论和类型理论讨论。然而，为了将操作性语义转换为指示性语义，仍然需要借助一些类型理论和范畴论知识。在基于λ演算的类型理论看来，数学中的纯函数f(x)和g(x)，用λ演算可表示为f(x)=λx.e1和g(x)=λx.e2，e1和e2表示任意表达式。数学中的纯函数组合h(x)=(g∘f)(x)，根据λ演算的β法则可表示为h(x)=(λx.e1)[e2/x]，[e2/x]表示用e2替换表达式e1中出现的所有非自由变量x。在正式的ML系列编程语言编译器的实现中，λ表达式的语法为f(x)=funx→e1，β法则一般用可读性较好的正式语法letx=e2ine1表示。因此，数学中的纯函数组合h(x)就可以编码为λ表达式，即h(x)=(funx→e1)e2，等价于用let…in…编码为了h(x)=lety=e2ine1。

但非纯函数f:A→TB和g:B→TC无法直接组合为h:A→TC，因为f的陪域为TB，而g的定义域为B，TB≠B。所以，意味着非纯函数无法直接编码为λ表达式或let语句，因为两个非纯函数无法直接组合。解决问题的关键在于要先将类型理论中的类型映射到范畴论的对象上，将类型理论中的函数映射到范畴理论中的态射上，再通过范畴中的Kleisli范畴进行非纯函数的组合。

(1) 将类型理论中的基本类型用范畴理论的对象解释。例如，[[τ]]=τ。

由于主要关心非纯函数的组合问题，因此简化为只考虑类型理论中的非纯函数如何用Kleisli范畴表示。如图所示，左边是先前的Kleisli范畴，右图是将操作性语义对应到指示性语义。其中类型α对应到范畴论的对象A，类型αt对应到范畴论的对象TA。类型理论中的表达式e1和e2对应到范畴论中的态射。在Klesili中非纯函数f转换为纯函数f*的操作就是bind(也称为lift，或>>=)，即f*=bindηAf。与之对应，将操作性语义转换后的指示性语义后，就把原来将带有效果的函数λx.e1转化为不带效果可以组合的函数，用let语句表示就是[[letx=e1ine2]]=bind[[x]][[λx.e1]]，如图6所示。

图6 用Klesili转化为指示性语义

3 核心代码分析

核心代码是把Miller等定义的auth和unauth语义进行Monad转换。以下分析过程中，其为了方便讨论，并未将x:TB写为准确的OCaml的语法类型x:βt，默认认为在范畴论CCC的理论框架下，TB等价于类型理论的βt。范畴论中表示对象的{A,B,C,…}符号等价于类型论类型变量{α,β,γ,…}的符号，两者在以下讨论中可以相互替代。

3.1 Auth分析

Auth是将经过认证数据的证明流proof写入到磁盘上，因此auth程序的行为与write行为相似，属于write monad。假设proof为加密后的字符串。为了方便讨论，将其简化为Σ*={a,b,c,…}形式，表示为所有字符组成的有限字符串序列。令表示空加密字符串，那么hash(a,b)就可以想象为两个字符串之间的某种组合操作(例如，字符串按位异或操作)。将此操作定义为•，那么v=s•t就表示v是s和t的一种组合结果。

proof≌Σ*={a,b,c,…}

noproof≌=[]

auth程序的行为可描述为输入类型A的数据，输出结果为类型B的数据，同时生成代表证明流proof的字符串Σ*，并将其写入到磁盘上。Σ*是函数产生的效果。函数f可以表示为(假设，TB=B×Σ*，TC=C×Σ*)：

f:A→TB=f:A→B×Σ*

此时f(a)=(b,s)的含义是：如果输入数据为a，那么f(a)表示在返回数据b的同时，将生成写入磁盘的证明流s。为了能让非纯函数f(x)和g(x)可以组合，则必须满足下面两个条件才能构成Monad。

当输入为a时，由单位函数定义可知，单位函数输入和输出结果应保持一致，而且不会产生证明流，因此id(a)=(a,)。由图3和图6可知，id就是Monad中的ret。因此，ret(a)=(a,[])。与之对应的OCaml代码为let returna=(a,[])。

当输入为a时，令f(a)=(b,s)且g(b)=(b,t)。表示f产生结果b并生成证明流s。当两个函数组合时，g需要输入数据b，并产生证明流t，即(g∘f)=(c,s•t)。

(g∘f)(a)

1.≈ (λx.g)(f(a))

2.≈ letx⟸f(a) ing(x)

3.= letx:TB⟸f(a:A):TB

ing(x:B):TC

4.= letx:TB⟸ (b,s):TB

ing(x:B):TC

5.= let (m,n):B×Σ*⟸ (b,s):B×Σ*

ing(x:B):TC

6.= let (m:B⟸b:B,n:Σ*⟸s:Σ*):TB

ing(x:B):TC

7.=g(x:B⟸b:B):TC

8.= (c,s•t)

为了检查数据类型是否保持一致，第3行开始添加数据对应的类型。例如，x:TB表示变量x的数据类型是TB。从第6行到第7行后，数据s是否与数据t进行•操作由g(x)的内部实现确定，因此s应出现在g(x)的具体代码实现中。就具体示例来说，由于证明流是需要进行Hash连接的，因此s•t确实进行了字符串连接操作。

与上述过程对应的OCaml代码实现如下。

let (>>=) (prf,a) f= (*>>=表示Monad绑定*)

let (prf′,b)=f a in (*lety=e2ine1*) (prf @ prf′,b) (*TB*)

3.2 Unauth分析

Unauth从磁盘上读取经过加密的数据流，根据Merkle树从叶节点到根节点的路径逐个节点解密，如果解密后的证明流满足Hash值要求，则接收，否则报错。unauth程序的行为类似于parser monad。与3.1节类似，为了方便讨论引入Σ*表示证明流。unauth程序的行为可描述为输入(A,Σ*)数据是product类型，结果满足Hash运算要求时输出为(B,Σ*)，否则程序输出异常E。这表明输出数据类型是sum类型数据(B,Σ*)+E。

f:A→TB=f:A×Σ*→(B,Σ*)+E

注意到等式左边只有一个输入参数A，而等式右边输入参数是A×Σ*，也就是左右两边的输入参数不一样。根据Curring定理可知(Homset表示态射集合)：

Homset(A×B,C)≌Homset(A,CB)

令A×B=A×Σ*，C=(B,Σ*)+E，代入Curring展开公式则有:

Homset(A×Σ*,(B,Σ*)+E)≌Homset(A,((B,Σ*)+E)Σ*)

CB={Z|Z:B→C}表示所有从B到C的函数组成的态射Z。因此：

f:A→TB=f:A→(Σ*→(B,Σ*)+E)

即TB=Σ*→(B,Σ*)+E。将B代换为A结果不变，形式如下：

f(A)=TA=Σ*→(A,Σ*)+E

以下为了便于讨论，仍旧使用f(a,s)的形式，而不采用Curring展开式。f(a,s1)=(b,s2)+failed含义是当输入数据类型a和对应的证明流s1后，如果成功解析数据则得到数据b及其证明流s2，即(b,s2)；否则，引起异常，输出failed。为了能让非纯函数f(x)和g(x)可以组合，则必须满足下面两个条件才能构成Monad。

当输入为a时，由单位函数定义可知，id(a,s1)=(a,s1)。因此，ret(a,s1)=(a,s1)。与之对应的OCaml代码let returna=funproof→′Ok(a,proof)。注意，代码中使用了Uncurring形式，proof就是证明流。如果是两个函数的组合，当输入为(a,s1)时，令f(a,s1)=(b,s2)+E且f(b,s2)=(c,s3)+E，那么(g∘f)(a,s1)=(c,s3)+E。

形式为f(A)=A+B函数是sum类型，可用如下形式表示，语义等价于match…with…语句。函数组合可以如下进行化简。

(g∘f)(a,s1)

1.≈ (λx.g)(f(a,s1))

2.≈ letx⟸f(a,s1) ing(x,s2)

3.= let matchf(a,s1) with

| (b,s2)→g(x,s2)

|E→failed

最后一行通过match进行分支跳转，跳转后的代码分析与3.1节相似，此处省略。与上述过程对应的OCaml代码实现如下。

let (>>=) c f=

fun prfs→

match c prfs with

|、ProofFailure→、ProofFailure

|、Ok(prfs′,a)→f a prfs′

3.3 实现Merkle树和关键接口

为了能将提取出的可认证数据结构的语义信息进行编码，首先要明确Functor和Monad在程序语言中的表现形式。在OCaml中Functor通过Modular实现。OCaml中Functor和Monad机制与Haskell有所区别，主要是因为OCaml中没有Higher-Kind数据类型，而Haskell有表现Higher-Kind数据类型的Type-Class。用Haskell实现代码时，要专门寻找在Haskell中对应于Type-Class概念而设计的Functor和Monad机制。通过Modular机制将可认证数据结构抽象为签名：

module type AUTHENTIKIT=sig

在创建表示新添加的可认证数据类型时，需通过类型构造器创建auth类型，并将该类型提交给OCaml编译器。按照编程方法的约定，此时只需要表现数据结构的形式，而不需要有具体代码实现，也就是在AUTHENTIKIT中写出所有要用到数据的抽象语法。

可认证计算需要生成证明流以供数据验证方使用。 在代码实践时，原来的可认证计算过程是运用 Hack 技术通过 Campl4 直接写入到 OCaml 编译器 。 但通过Monad 可以将写入到编译器中的可认证语义提取出来，如代码段1所示。 第1行代码定义了抽象可认证计算类型，以参数多态形式表现。第2行定义了返回函数，本质就是η。第3行定义了 bind 操作， 本质是定义了函数组合方式。

代码段1(可认证计算的Monad接口)：

1. type ′a auth

2. type ′a authenticated_computation

3. val return: ′a->′a authenticated_computation

4. val(>>=): ′a authenticated_computation->

(′a->′b authenticated_computation)->

′b authenticated_computation

在代码中产生附加效果的数据类型用TA=′aτ表示，附加效果中含有需要的证明流和待验证数据，而其中τ=authenticated_computation。数据绑定过程就是Monad理论中的μ合并数据过程，其中bind就是符号>>=，用公式表示是:

bind:A→TB=(A→TA)→(B→TB)→(A→TB)

如果令A=()单位输入，则上述公式变为:

bind:A→TB=(()→TA)→(B→TB)→(()→TB)

由于根据范畴论，可以省略，所以公式变化为:

bind:A→TB=TA→(B→TB)→TB

这就是代码中第4行绑定数据的形式。由于最后计算结果是A→TA，因此需要η说明id函数的计算过程，这就是代码中return方法所起到的作用。实际计算是从A开始，通过lift操作得到TA，然后解析出TA中的A，再通过A→TB函数计算出带有效果的数值，最后将计算结果放到TB中。整个计算过程是两次扩展，首先将A的陪域扩展为TA，然后将B的定义域扩展为TB，最后将两个函数连接起来求出TB。

另外还需证明需要验证的数据流是“可认证的”。本质上相当于需要确保写入到磁盘上的证明流是连续的，如果在写入证明流时，写入过程被其他线程打断，那么所写入的证明流可能由于不连续而出错。在原论文中默认写入到磁盘的证明流是连续不会被打断的，以这种方式改写编译器内核后，可能会导致出现无法跟踪的错误情况。因此当假设写入证明流过程可能会被打断的时候，就需要采用更为正式的方式来验证证明流的完整性。只有当验证证明流是完整之后，才能继续后面的工作。所以需要加入代码2所示的接口Authenticatable。

代码段2(防止证明流被打断代码接口)：

module Authenticatable: sig(*防止证明流被打断*)

type′a evidence

val auth: ′a auth evidence

val pair: ′a evidence->′b evidence

->(′a*′b) evidence

val sum: ′a evidence->′b evidence

->[′left of ′a|′right of ′b] evidence

val string: string evidence

val int: int evidence

end

可明显看出，这是创建树中节点的过程。通过pair就能合并两个叶子节点的哈希值，通过sum可将左或右叶子节点的数值合并到当前节点中。

由于在接口中添加了一层新的验证数据流完整性的接口，因此所有需要验证的数据都必须先经过此接口才能继续验证。也就是，创建证明路径和解析Merkle树的完整过程都可观察。对验证过程来说，要确保所有待验证或待写入数据都是完整不被打断的读取或写入的过程。

unauth函数返回Monad计算中验证的数据后，如果有证明路径信息，加上现在获取的验证信息，表示接下来就对可认证数据结构开展验证工作。代码段3所示代码最终定义了auth和unauth函数。从代码行可以看出，两者输入时都要求有Authenticatable类型数据，即要求数据是连续的完整的数据。

代码段3(auth和unauth定义代码接口)：

valauth: ′a Authenticatable.evidence->′a->′a auth

val unauth: ′a Authenticatable.evidence->′a auth->

′a authenticated_computation

在AUTHENTIKIT中需要添加基本Merkle树结构。树的实现有很多种方法，但每种实现方法都与具体要传输的信息结构密切相关。因为是在网络中传输结构化信息，所以最方便的方式是使用JSON数据格式。OCaml自身提供了多种JSON数据格式转换库以供调用，可以很方便用数组形式实现树形结构。基本Merkle树需要提供计算叶子节点哈希值功能，由makeleaf函数实现。通过哈希方式合并非叶子节点并计算出合并后哈希值功能的函数由make_branch函数实现。在构造Merkle树时，只需要上述两个函数即可。为了测试目的，提供了两个测试函数，分别是用于retrieve和update函数用于检索和更新Merkle上的节点。

由于Prover和Verifier都要通过同一个Merkle结构来访问可认证数据流，因此Merkle树应该是一个函子：

moduleMerkle: MERKLE=

functor (A: AUTHENTIKIT)->struct; open A; …

也就是说，当需要使用Merkle树的是Prover时使用Prover提供的功能访问Merkle树，当需要使用Merkle树的是Verifier时就用Verifier提供的功能访问Merkle树。需要注意的是，此处OCaml的Functor与Haskell中Functor在范畴论上是同一概念，但在具体编程实践上是两个不同的概念。前者属于类型理论中的*→*数据类型，后者属于类型理论中的Higher-kind数据类型，即属于•→•类型。

Merkle树接口的定义与实现部分与Monad无关，是完全抽象出来的一个数据层。完全可以将Merkle树的实现当作一个普通的数据结构。只有当Prover和Verifier这两个模块作为参数传递给Merkle树的时候，Monad接口才会与之发生松耦合的联系。在Merkle树看来，auth和unauth就像两个新的语法特性一样。

与原论文所不同的是，新实现的auth和unauth是作为库文件功能提供给Merkle树使用，在增添新的语法功能时，并没有修改OCaml编译器的抽象语法树。因此，可认证功能将直接使用OCaml的类型检查算法和错误报告机制，在编译源代码时，如果错误使用了auth或unauth的调用方式，OCaml就会给出提示信息。

4 新方法的改进之处

4.1 原方法的局限性

原方法的局限性是比较复杂且不够通用。原方法是先用Camlp4分析OCaml编译器的语法树，然后再通过Hack OCaml的技术在编译器内部语法树上添加自定义关键字的语法属性。

由于需直接修改编译器内部复杂的抽象语法树，导致基于修改语法树实现的方法也非常复杂。不够通用是因为各种编译器内部语法树都有所差异，且并不是所有编译器都公开内部编译器语法树，所以这种方法并不适用于所有编译器。

原方法在实现时，必须要首先了解OCaml编译器内部语法树的属性和规则，找到语法描述结构，然后才能裁剪抽象语法树，添加关键字的属性。抽象语法树结构整体十分复杂，只有通过OCaml的提供的接口才能添加新的语法属性。

如果希望添加新的语法关键字，在具体实现时同样需要先分析抽象语法树。每种编译器的抽象语法树都略有不同，分析对象就会有差异性。有些编译器并未公开内部语法树结构，因此无法通过Hack内部语法树结构的方法添加新的语法功能。

4.2 新方法的特点

通过Monad将编译器中一小部分操作性语义转化为等价的指示性语义。在实现时，Monad并未向编译器语法树引入新语法属性，基于OCaml自身的语法实现了添加新语言特性的目标。这种只使用源语言的语法就能产生新语言特性Monad方法普遍适用于函数式编程语言。不需要语言特性设计者深入了解修改编译器语法树，也不需要修改源语言的语法。

使用Monad方法创建认证数据结构的方法具有通用性。只要程序语言编译器具有最一般性的类型推导系统，就能通过该方法将抽取出的证明流的语义写入到库文件中，形成新的语言特性。例如，Haskell是另外一种函数式程序语言编译器，同样也能通过Monad方法，在仅使用Haskell自身语言语法，便可实现在程序语言中引入可认证数据结构语言特性。

5 结 语

本文通过完整展示将可认证数据结构的操作性语义转化为指示性语义的过程，阐述了Monad的理论概念如何对应到的具体实践的编程概念。由于Monad概念过于抽象，所以本文重点描述了auth和unauth代码的分析过程，以具体实例展示如何将非纯函数组合在一起。采用Monad方法可直接借助源编译器语言实现新的语言功能，因此可避免修改编译器的语法树，同时便于在不同程序编译器之间移植新的语言功能。