土壤结构对城轨中杂散电流分布的影响分析

周 奇，林 圣，邹全德，李昱达

（西南交通大学电气工程学院，成都 610031）

城市轨道交通主要采用直流供电，由于钢轨无法与大地完全绝缘，使得钢轨对地具有一定的钢轨电位，导致部分电流从钢轨泄漏至大地，形成杂散电流[1]。城市轨道交通以其运量大、绿色环保等优势得到快速发展。地铁线网的大规模、高密度运行带来了严重的杂散电流问题。杂散电流不仅会加速隧道结构钢筋、接地网、地铁线路周围的天燃气管道、水管等埋地金属的腐蚀[2-4]，还会流入城市电网接地变压器导致变压器出现直流偏磁[5-7]现象，危及变压器运行安全。如上海地铁2号线沿线世纪大道下的燃气管道，由于杂散电流腐蚀，已经发生了数十次泄漏事故[4]；深圳市500 kV深圳站主变压器由于长期处于直流偏磁振动异常状态，导致出现绝缘抱箍松动、紧固件松脱、绕组过热等情况，严重威胁主变压器运行安全[7]。为此，国内外已发布了一系列标准用于防治杂散电流[1,8]。然而，城市轨道交通跨度大，且沿线土壤地质环境复杂，因此，有必要就土壤结构对杂散电流分布的影响展开研究，以指导杂散电流防治。

大地土壤随着深度的增加而呈现不同的类型，且表现出不同的电阻率。典型的土壤分层结构由上至下依次为：有机质层、表土层、淀积层、风化层、基岩层[9]。在电力系统行业已经就土壤分层结构对接地设备的性能开展了广泛研究。如文献[10]考虑土壤水平分层结构提出了一种基于复镜像法获取土壤电阻率的方法，提高了土壤电阻率计算精度。文献[11]考虑土壤结构对接地电阻的影响，建立了直流分布的完整计算模型，探讨了多层水平土壤情况下直流分布的规律。文献[12]考虑冲击电流在分层土壤中的散流过程具有明显的非线性变化特征，从电磁场理论出发，建立了分层土壤结构中接地装置冲击特性分析的有限元模型。文献[13]基于国际接地计算软件CDEGS，仿真分析了土壤各层电阻率及厚度对接地网接地电阻的影响规律。

同样地，城市轨道交通中由钢轨、排流网、辅助排流网构成的回流系统性能也受土壤结构的影响。文献[14]考虑城市轨道交通沿线土壤电阻率均匀分布仿真分析了杂散电流的动态特性。文献[15]仿真分析了沿地铁线土壤电阻率不均匀分布情况下沿线杂散电流分布，仿真结果表明随着土壤电阻率的增加，排流网收集效率增加。文献[16]考虑分层土壤结构建立了杂散电流计算的集总参数模型，仿真分析了均匀土壤结构和多层土壤结构工况下，杂散电流对埋地管道对地电位的影响。可见土壤结构是影响杂散电流大小和分布的因素之一，但各层土壤厚度及电阻率对杂散电流分布的影响尚不明确。为此，本文搭建了含分层土壤结构的杂散电流仿真模型。进一步分析了均匀土壤、分层土壤中电阻率、土壤厚度等对杂散电流分布的影响。

1 含分层土壤结构的杂散电流仿真模型

城市轨道交通的直流供电系统主要由牵引所、牵引网、回流系统和列车等部分组成，如图1所示。

图1 直流牵引供电系统Figure 1 DC traction power supply system

根据系统的结构，考虑杂散电流的流动路径，构建如图2所示的杂散电流仿真模型。该模型为二维平面的电阻网络结构，图中每个电流源表示牵引所或者列车。每个电流源的位置和实际牵引所或者列车的位置吻合，其具体的取值需要通过潮流计算获得[17]。基于此，牵引供电系统被m个电流源划分为(m+n-1)个计算区间，m表示列车数量，n表示牵引所数量。每个区间由多个微分电阻组成。模型中Rr表示钢轨纵向电阻，其取值取决于钢轨材料、焊接工艺和钢轨腐蚀程度等多方面因素，通常可通过测试或者合理估计确定。考虑钢轨的腐蚀，Rr的取值范围为15～40 mΩ/km。Rs表示排流网电阻，Re表示辅助排流网电阻，二者取值均取决于排流网材料、钢筋数量、钢轨间距、混凝土电阻等因素。Rd表示等效大地电阻，取值取决于土壤结构。

图2 杂散电流仿真模型Figure 2 Stray current simulation model

在分层土壤结构中，不同土壤层存在不同的电阻率和深度。以深圳市为例，其大陆区区域的等效土壤分层依次为：有机质层、表土层、淀积层、基岩层[18]，深度分别为0、15、35、45 m，电阻率分别为200、600、50、5 000 Ω·m。而不同地区由于其环境气候等因素，土壤分层结构存在差异。基于此，本文构建了含任意多层土壤结构的杂散电流仿真模型，等效多层土壤结构的建模如下。

考虑到杂散电流在一定范围内传播，大地土壤被等效为正方体结构，如图3所示。l表示杂散电流的传播范围，其值可以基于土壤电阻率等因素的考虑进行合理设置。dx表示x方向的单位长度，即列车运行的方向。hm表示第m(m=1，…，u)层土壤的厚度，u表示总的土壤层数。ρm(m=1，…，u)表示第m层土壤的电阻率。在分层土壤结构中，ρm和hm的取值通常可从地质部门获得，也可以采用实测反演的方法来确定[19]。式中，土壤模型中最后一层土壤层hu的厚度可以通过公式(1)确定。

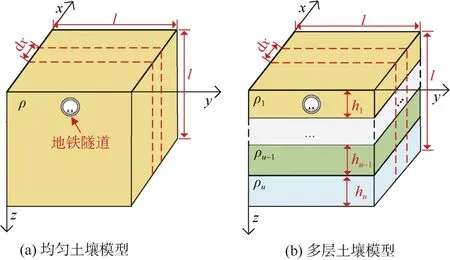
图3 等效土壤模型Figure 3 Equivalent soil model

当u=1时，大地为均匀土壤结构，图2中的大地电阻可通过公式(2)进行估计。当u≠1时，大地为多层土壤结构，每一层土壤电阻由Rsm(m=1，…，u)表示，通过公式(3)估计。进一步地，考虑多层土壤在水平方向上的并联结构，则大地电阻可以被估计。

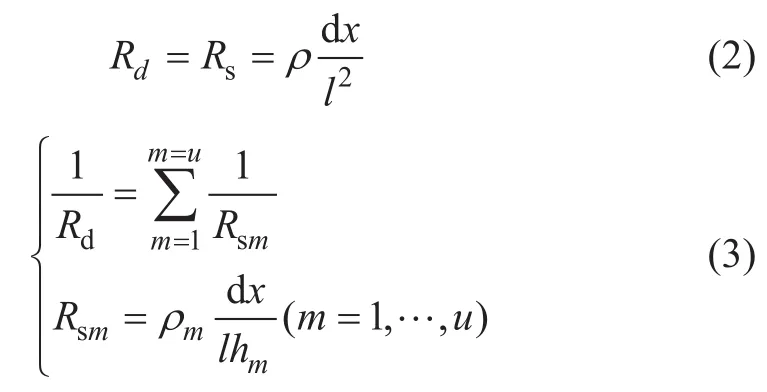
Ga、Gb、Gc、Gd、Ge、Gf分别表示杂散电流仿真模型中各电阻层之间的电导。其中Ga、Gd、Gf主要由扣件材料、绝缘垫性能等因素决定，标准中规定钢轨对地电阻或钢轨对排流网电阻需要大于15 Ω/km，即相应电导需要小于 0.06 S/km。Gb主要取决于混凝土电阻和尺寸，混凝土电阻通常为10～250 Ω/km。上述电导值几乎不受到土壤结构的影响。然而排流网对地电导Ge和辅助排流网对地电导Gc需要考虑土壤结构变化带来的影响。借鉴多层土壤结构对接地网接地电阻的研究，Ge和Gc可以通过矩量法或者通过CDEGS仿真获得[20]。

杂散电流仿真模型的微分单元如图4所示。为了求解杂散电流分布，基于基尔霍夫定律建立任意位置的基尔霍夫电压和电流方程(4)，其中F表示微分单元中的电压和电流，如公式(5)所示，X表示电阻网络矩阵。

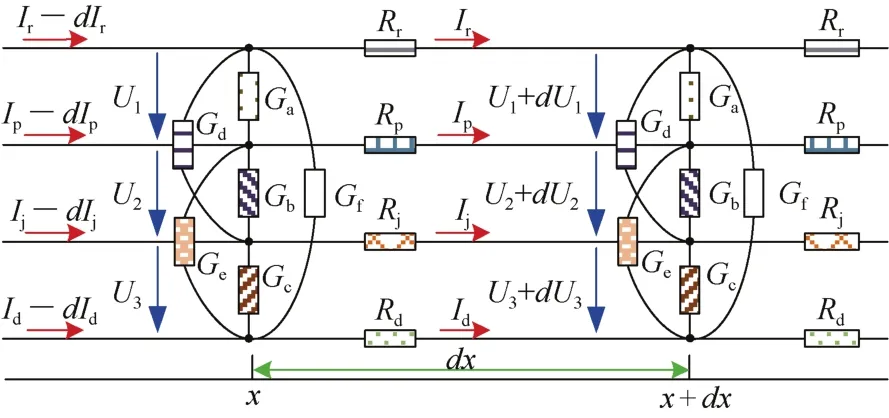
图4 杂散电流仿真模型的微分单元Figure 4 Differential element of the stray current simulation model

对基尔霍夫方程进行整理化解，可以获得任意位置处的电压和电流的解析解，如公式(6)所示。F是关于任意位置x的函数，其中D和α分别是电阻网络矩阵X特征向量和特征值，k是待求的未知系数。电流源作为边界条件，可计算解析解中的未知系数k。

杂散电流表示不按规定路径流通的电流。因此，任意位置处的杂散电流可以通过公式(7)求解。

2 分层土壤对杂散电流的仿真分析

某地铁线采用1500 V直流供电，站点如图5所示。沿线共有10个车站，含5个牵引所，总距离为10.73 km。假设沿地铁线路参数均匀分布，杂散电流仿真模型的主要参数如表1所示[21-23]。

表1 杂散电流仿真模型主要参数Table 1 Main parameters of the stray current simulation model

图5 地铁站点分布Figure 5 Distribution of metro stations

假设沿线运行列车有4列，其位置和功率分布如表2所示。基于此，搭建杂散电流仿真模型。通过调整等效土壤模型，开展土壤结构对杂散电流的仿真分析。

表2 列车位置和电流Table 2 Train position and current

列车位置和电流作为输入数据，通过潮流计算方法可获得地铁线各牵引所电流分布，如表3所示。由表3可知，列车1所在区间两端的牵引所电流为正值，而其他牵引所电流为负值。

表3 牵引所电流Table 3 Traction power substation current

2.1 土壤结构对杂散电流的影响分析

为了分析土壤结构对杂散电流的影响，考虑均匀土壤结构和双层土壤结构建立了杂散电流计算模型。排流网和辅助排流网均简化为单根导体，可通过CDEGS估算不同土壤结构中的电导Gc和Ge，如表4所示。假设其他参数不随土壤结构的变化而变化。在此基础上，仿真杂散电流和钢轨电位，如图6所示。排流网、辅助排流网和大地中的电流如图7所示。

表4 均匀土壤模型和双层土壤模型中的仿真参数Table 4 Simulation parameters in different soil models

图6 仿真结果Figure 6 Simulation results

图7 不同土壤结构中排流网电流Ip、辅助排流网电流Ij和大地电流IdFigure 7 The current distribution in the stray current collection mat Ip, tunnel reinforcement Ij, and ground Id under different soil model conditions

仿真结果表明，沿线钢轨电位最大值出现在列车1的位置处，最大值为59.13 V。杂散电流最大值出现在线路1/4的位置处，最大值为9.96 A。此外，进一步分析可见，双层土壤结构对总杂散电流分布和钢轨电位分布影响不大。由于钢轨泄漏的杂散电流主要取决于钢轨的绝缘性能，而钢轨绝缘性能主要取决于钢轨扣件、绝缘垫等结构[24-25]，不受到土壤结构的影响。因此双层土壤模型中的杂散电流分布与均匀土壤模型相同。钢轨电位主要取决于钢轨相关的电阻参数和钢轨电流。而钢轨相关的电阻参数没有变化，钢轨电流在不同工况中几乎一致。因此，钢轨电位也是相同的。

在工况 A1中，大地电流远高于排流网和辅助排流网中的电流，大地电流的最大值为5.89 A。在工况A2中，辅助排流网中的电流高于其他结构中的电流，最大值为5.16 A。而大地电流几乎为零，这是由于在A2中大地电阻远远大于其他结构。在工况A3中，排流网中的电流高于其他结构中的电流，最大值为4.32 A。与均匀土壤结构相比，双层土壤结构中排流网和辅助排流网中的电流增加。这是因为在双层土壤结构中，排流网和辅助排流网对地的电导较小，因此泄漏的电流较少。此外，由于排流网和辅助排流网中积累了更多电流，因此，双层土壤结构大地电流更少，而更少的大地电流意味着更少的埋地金属腐蚀。

2.2 土壤电阻率对杂散电流的影响分析

基于均匀土壤模型仿真分析了不同土壤电阻率对沿线杂散电流的影响，仿真工况如表5所示。由上节分析可知，土壤模型的改变几乎不影响沿线钢轨电位和总的杂散电流分布。为此，在本节及以下仿真分析中仅给出了不同工况下排流网、辅助排流网和大地电流分布。不同土壤电阻率下的仿真结果如图8所示。

表5 不同土壤电阻率下的仿真参数Table 5 Simulation parameters under different soil resistivity

由图8可知，在仿真工况B1中，大地电流远远大于其他结构中的电流，且最大值为5.94 A。在仿真工况 B2中，辅助排流网中的电流是最高的，最大值为4.51 A。在仿真工况B3中，排流网中的电流是最高的，最大值为5.23 A。随着土壤电阻率的增加，大地电流逐渐减小，排流网中的电流随着土壤电阻率的增加而增加。首先大地电阻随土壤电阻率的增大而增大；其次随着土壤电阻率的增加，排流网和辅助排流网的对地电导逐渐降低。因此，随着土壤电阻率的增加，排流网和辅助排流网将积累更多的电流。

图8 不同土壤电阻率中排流网Ip、辅助排流网Ij和大地电流IdFigure 8 The current distribution in the stray current collection mat Ip, tunnel reinforcement Ij, and ground Id under different soil resistivity

2.3 分层土壤厚度对杂散电流的影响分析

构建双层土壤模型，设置首层土壤深度为0 m，电阻率为10 Ω·m，第2层土壤深度为10 m，电阻率为1000 Ω·m。通过调整土壤首层厚度，仿真分析了土壤层厚度对沿线杂散电流的影响，仿真工况如表6所示。排流网、辅助排流网和大地电流分布如图9所示。

表6 不同土壤层厚度下的仿真参数Table 6 Simulation parameters under different soil layer thickness

由图9可知，在仿真工况C1中，辅助排流网中电流远远大于其他结构中的电流，且最大值为5.16 A。在仿真工况C2中，同样是辅助排流网中的电流最高，且最大值为5.17 A。随着土壤首层厚度的增加，大地电流逐渐增加，排流网中的电流逐渐减少。由于大地电阻随土壤首层的厚度增加而减小，因此大地中的电流逐渐增加。在3.097 km处，大地电流为1.60 A，增加了3.86倍。

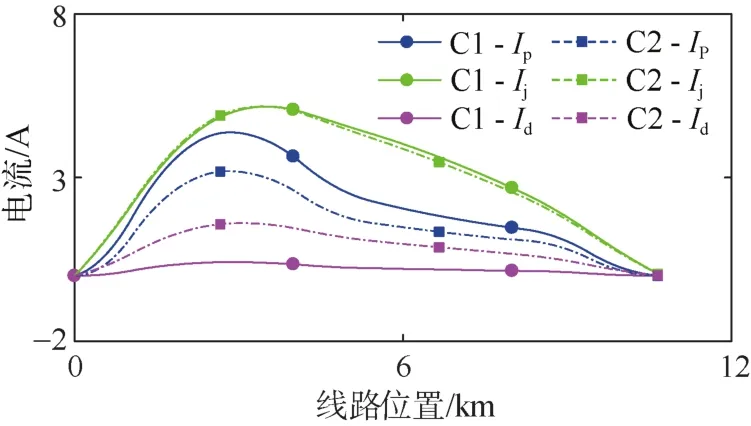
图9 不同土壤层厚度中排流网Ip、辅助排流网Ij和大地电流IdFigure 9 The current distribution in the stray current collection mat Ip, tunnel reinforcement Ij, and ground Id under different soil layer thickness

2.4 分层土壤电阻率对杂散电流的影响分析

构建双层土壤模型，设置首层土壤深度为0 m，厚度为10 m；第二层土壤深度为10 m。通过调整首层和第2层土壤电阻率，仿真分析了分层土壤电阻率对沿线杂散电流的影响，仿真工况如表7所示。排流网、辅助排流网和大地电流分布如图10所示。

表7 不同分层土壤结构下的仿真参数Table 7 Simulation parameters under different layered soil structures

图10 不同分层土壤结构下排流网、辅助排流网和大地的电流Figure 10 The current distribution in the stray current collection mat, tunnel reinforcement, and ground under different layered soil structures

由图10可知，在仿真工况D1中，辅助排流网中电流大于其他结构中的电流，且最大值为5.16 A。在仿真工况D2中，辅助排流网中的电流同样是最高的，最大值为4.68 A。在仿真工况D3中，排流网中的电流是最高，最大值为4.32 A。在仿真工况D4中，排流网中的电流最高，最大值为4.70 A。此外，大地电流在仿真工况D1和D2中最低，接近于零，D1中大地电流最大值仅为0.41 A。更小的大地电流意味着更少的埋地金属腐蚀。考虑更为准确的土壤结构可以更为准确地评估杂散电流对埋地金属腐蚀的影响。比较图10中的D1和D2，可以发现当土壤首层电阻率增大时，辅助排流网和大地中的电流减少，排流网的电流增加。由于土壤首层电阻率增加，大地电阻增加且排流网和辅助排流网对地电导减弱。基于此，排流网中电流是更大的，因为流出排流网的电流更小。从排流网流入辅助排流网的电流减少，所以辅助排流网的电流是减少的。比较图10中的D3和D4，可以发现随着第二层土壤电阻率增加，大地电流是减少的，而排流网和辅助排流网中的电流是增加的，这也可以基于上述理论进行解释。

3 结论

本文建立了含土壤模型的杂散电流仿真模型，仿真分析了土壤结构对杂散电流的影响。仿真分析表明土壤模型会影响排流网、辅助排流和大地中的电流分布，而对沿线钢轨电位和总的杂散电流分布几乎没有影响。土壤模型对排流网、辅助排流网和大地中电流分布的影响是复杂的，这取决于土壤模型参数的综合影响。在均匀土壤模型中，土壤电阻率越大，流向大地中的电流越少。在分层土壤结构中，首层土壤厚度越小或电阻率越大，流向大地中的杂散电流越少。大地中的电流越少，意味着更少的埋地金属腐蚀。