Digraph states and their neural network representations
Ying Yang(杨莹) and Huaixin Cao(曹怀信)
1School of Mathematics and Information Technology,Yuncheng University,Yuncheng 044000,China
2School of Mathematics and Statistics,Shaanxi Normal University,Xi’an 710119,China
Keywords: digraph state,neural network,quantum state,representation
1. Introduction
In quantum physics, fully understanding and characterizing a complex system with a large number of interacting particles[1]is an extremely challenging problem. Solutions within the standard framework of quantum mechanics generally require the knowledge of the full quantum many-body wave function. Thus, the problem becomes how to solve the many-body Schr¨odinger equation[2–4]of the system with a large dimension. This is just the so-called quantum manybody problem (QMBP)[5–7]in quantum physics, which becomes a hot topic in high energy physics and condensed matter physics. When the dimension of the Hilbert space describing the system is exponentially large, it becomes a big challenge to solve the QMBP even with the most powerful computers.
To overcome this exponential difficulty and solve the QMBP, many methods have been used, including tensor network method (TNM)[8–10]and quantum Monte Carlo simulation (QMCS).[11]However, the TNM has difficulty to deal with high dimensional systems[12]or systems with massive entanglement.[13]The QMCS suffers from the sign problem.[14]Thus,some new methods are necessary for finding QMBPs.
The approximation capabilities of artificial neural networks (ANNWs) have been investigated by many authors, including Cybenko,[15]Funahashi,[16]Hornik,[17,18]Kolmogorov,[19]Roux.[20]It is known that ANNWs can be used in many fields, including representing complex correlations in multiple-variable functions or probability distributions,[20]studying artificial intelligence through the popularity of deep learning methods,[21]developing an artificial neural network potential for Au clusters,[22]and so on.[23–27]
Undoubtedly, the interaction between machine learning and quantum physics will benefit both fields.[28,29]For instance, in light of the idea of machine learning, Carleo and Troyer[30]found an interesting connection between the variational approach in the QMBP and learning methods based on neural network representations. They used a restricted Boltzmann machine(RBM)to describe the many-body wavefunction and obtained an efficient variational representation by optimizing those variational parameters with powerful learning methods. Chenet al.[31]discussed the general and constructive connection between the RBM and tensor network states (TNS). This equivalence sets up a bridge between the field of deep learning and quantum physics, allowing one to use the well-established entanglement theory of TNS to quantify the expressive power of RBM. Robevaet al.[32]showed the duality between tensor networks and undirected graphical models with discrete variables. Clark[33]used the framework of tensor networks to unify neural-network quantum states with the broader class of correlator product states. Huanget al.[34]proved that any(local)tensor network state has a(local)neural network representation.Leiet al.[35]proposed to utilize artificial neural network to determine the PT-phase-transition points for non-Hermitian PT-symmetric systems with shortrange potentials. Yinet al.[36]improved accuracy of estimating two-qubit states with hedged maximum likelihood. Yanget al.[37]researched approximation of unknown ground state of a given Hamiltonian with neural network quantum states.Numerical evidences suggest that an RBM optimized by the reinforcement learning method can provide a good solution to several QMBPs.[38–46]However,the obtained solutions are approximate, instead of exact ones. To find exact solution of QMBP with an ANNW, the authors of Ref. [47] introduced neural network quantum states (NNQSs) with general input observables from the mathematical point of view, and found someN-qubit states that can be represented by a normalized NNQS,such as all separable pure states,Bell states and GHZ states.
Graph states are a special class of pure multi-party quantum states, and they have extensive applications. Oneway quantum computation takes graph states as resources[48]and all code words in the standard quantum error correcting codes correspond to graph states.[49]Graph states have been produced in optical lattices[50]and the basic elements of one-way quantum computing have been demonstrated experimentally.[51]In Ref.[47],we determined the necessary and sufficient conditions for the representability of a general graph state using normalized NNQS for a given number of hidden neurons. Gaoet al.[52]proved theoretically that every graph state can be represented by an RBM with{0,1}-input and obtained the RBMRs of every graph state.
Spectra of quantum graphs display in general universal statistics characteristic for ensembles of random unitary matrices observed by Kottos and Smilansky in Refs.[53,54]. The quantization scheme of Kottos and Smilansky has been generalized to directed graphs (digraphs).[55–57]A digraph provide an intermediate step that gives explicit relationships between the process variables,human errors,and equipment failure events,from which the fault tree can be constructed.[58]It has many applications,e.g.,fault-tree synthesis,[58]fault propagation model[59]and design of sensor network.[60]
In this paper, we aim to define digraph states (directed graph)and construct explicitly the neural network representations (NNRs) of digraph states. In Section 2, some notations and conclusions on NNQS with general input observables are recalled and some related properties are proved. In Section 3,digraph states are proposed,and some properties are explored.In Section 4,the NNRs of digraph states are constructed.
2. Neural network quantum states

It is easy to check that the eigenvalues and corresponding eigenbases ofS=S1⊗S2⊗···⊗SNare

which is a nonzero vector(not necessarily normalized)of the Hilbert spaceℋ. We call it a neural network quantum state(NNQS)induced by the parameterΩ=(a,b,W)and the input observableS=S1⊗S2⊗···⊗SN(Fig.1).[47]

Fig. 1. Artificial neural network encoding an NNQS. It is a restricted Boltzmann machine architecture that features a set of N visible artificial neurons(blue disks)and a set of M hidden neurons(yellow disks).For each value Λk1k2...kN of the input observable S, the neural network computes the value of the ΨS,Ω(λk1,λk2,...,λkN).
The NNQWF can be reduced to
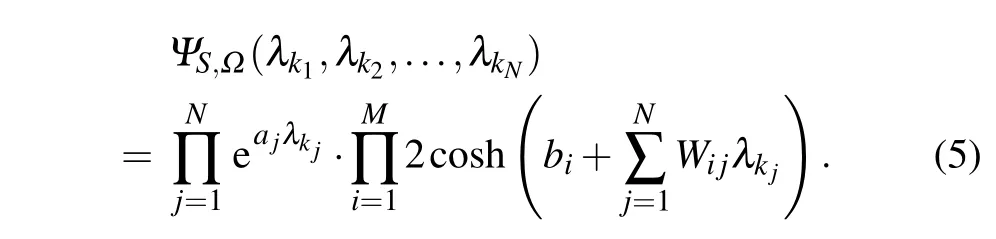
There is a special class of NNQSs:

This result can be illustrated by Fig.2.
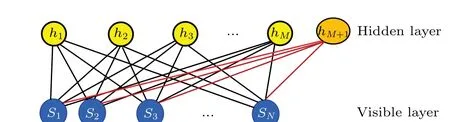
Fig. 2. The resulted network by adding a hidden layer neuron hM+1 into an network with visible layer S1,S2,...,SN and hidden layerh1,h2,...,hM.


3. Digraph states
In this section,we aim to introduce digraph states. To do this, let us start by introducing the definition of digraph. A digraph(or a directed graph)[57,62]is a pair-→G=(V,-→E)consisting of a setV={1,2,...,N}and a nonempty subset-→EofV×V. The elements ofVand-→Eare called vertices and edges of-→G,respectively. Whene=(i1,i2)∈-→E,we say thateis an edge of-→Gfrom the vertexi1to the vertexi2.
Given a digraph-→G=(V,-→E), we call←-G=(V,←-E) the inverse graph of-→G=(V,-→E),where
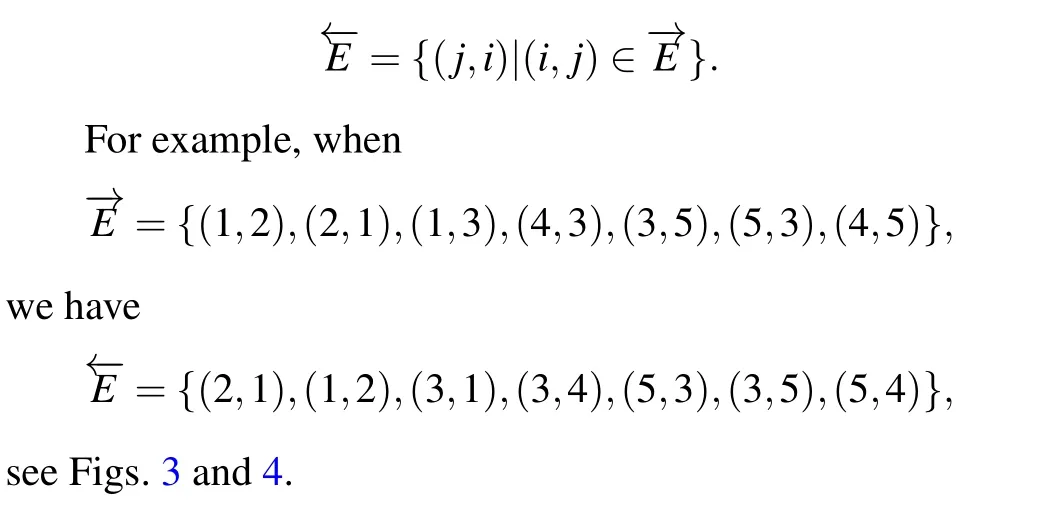
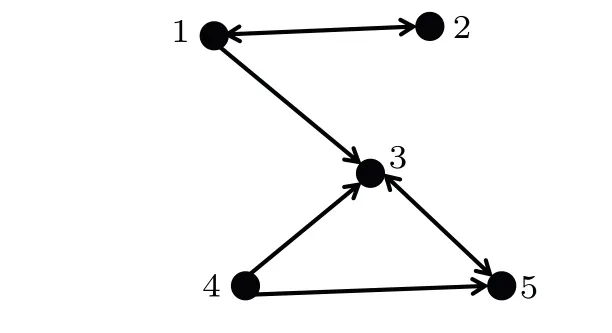
Fig.3. A digraph-→G.

Fig.4. The inverse graph of a digraph-→G.
Given a digraph-→G=(V,-→E), for each edge (i,j)∈-→Edefine an operator on theN-qubit system(C2)⊗N:
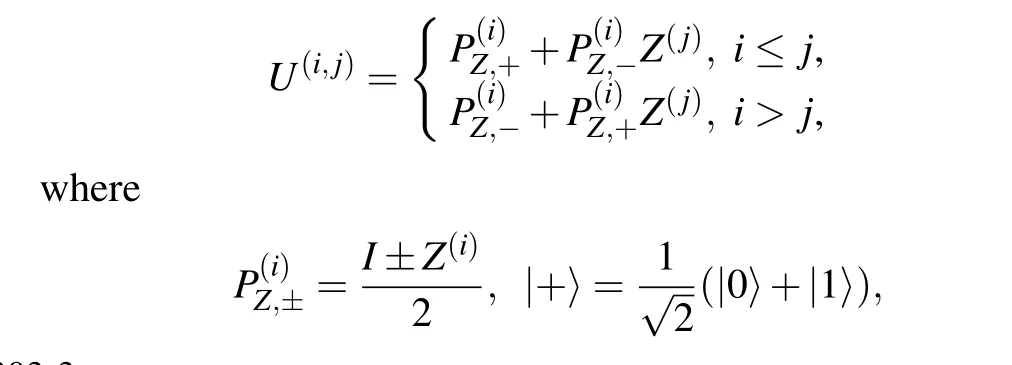
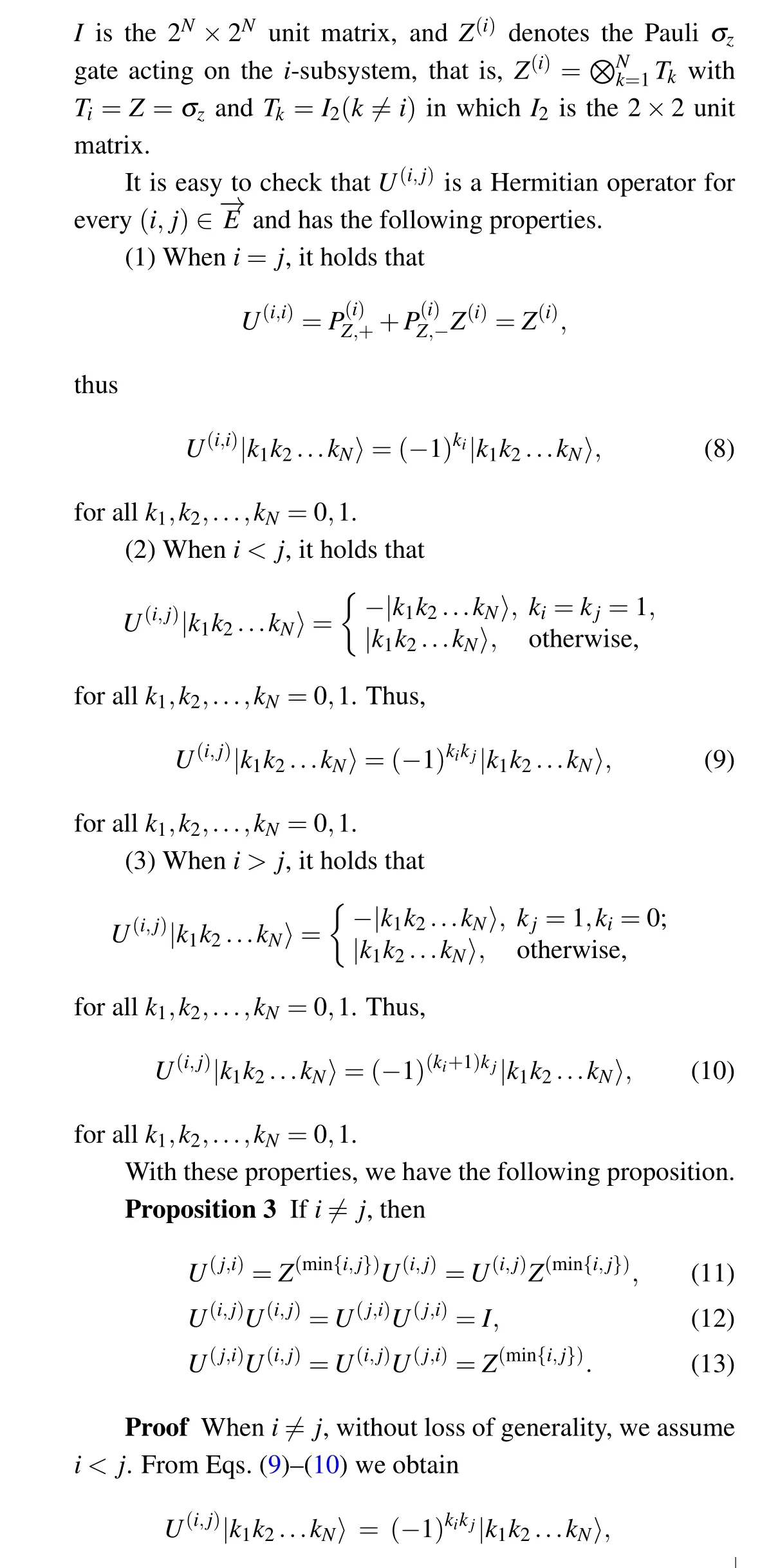

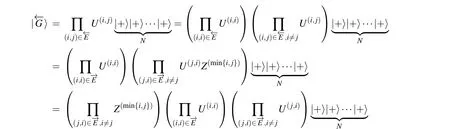
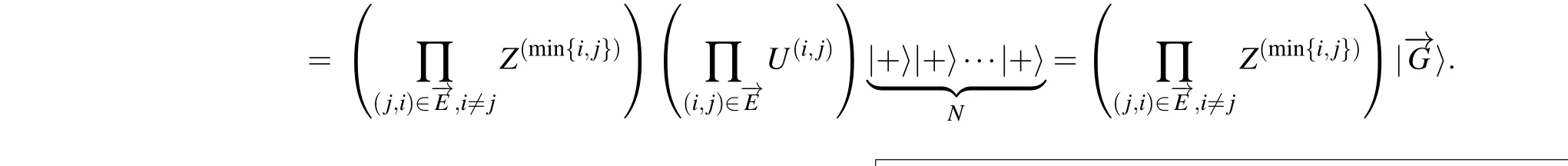
Next, we reduce the expression (14) of digraph state by the next procedure.




Let andλk1,...,λkN,|ψk1〉,...,|ψkN〉are shown in Eq.(6). We see that the simplified expression(15)is simpler and easier to use.Given a digraph,we can use this expression to obtain a digraph state associated to it very quickly.
For example,the digraph state|-→C3〉given by the digraph

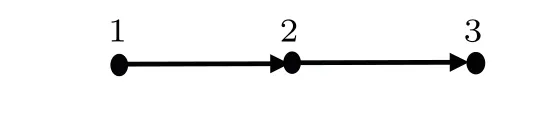
Fig.5. Digraph-→C3 with E0=E2=E3= /0,E1={(1,2),(2,3)}.

Fig. 6. Inverse graph of digraph -→C3 with E0 =E1 =E3 = /0, E2 ={(3,2),(2,1)}.



Fig. 7. The digraph -→C3 = ({1,2,3},{(1,2),(2,3)}) and the corresponding quantum circuit.
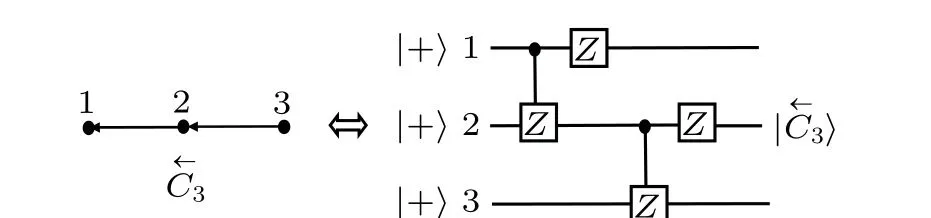
Fig. 8. The digraph ←-C3 = ({1,2,3},{(2,1),(3,2)}) and the corresponding quantum circuit.



Fig.9. Undirected graph C3 and the corresponding quantum circuit.

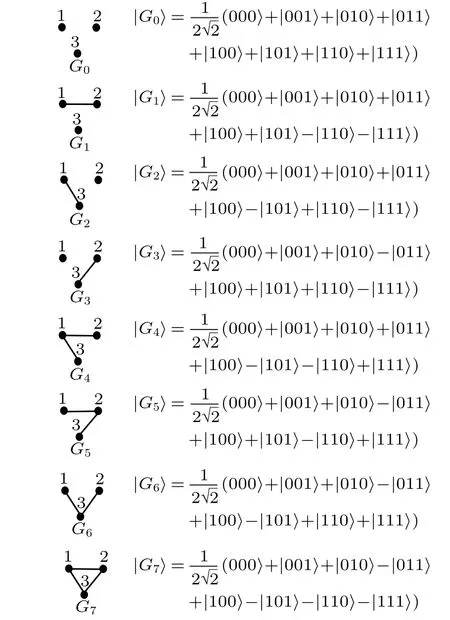
Fig.10. All possible graph states of three qubits.
4. Representing a digraph state as an NNQS
In this section,we construct a neural network representation of a digraph state|-→G〉using{1,-1}-input NNQS,that is,to find an NNQS|ΨS,Ω〉such that|-→G〉=z|ΨS,Ω〉,i.e.,



Fig.11. Neural networks representing the functionsfor(i,j)∈E1 ∖E3 and(j,i)∈E2 ∖E3,respectively.

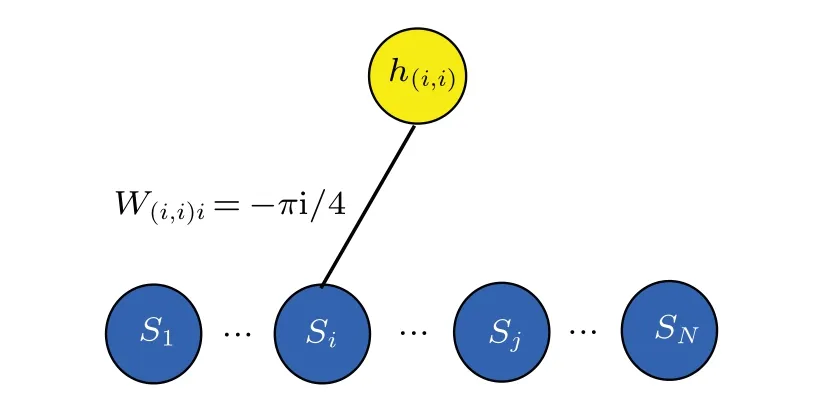
Fig.12. Neural network generating the functionfor any(i,i)∈E0.



Fig. 13. Neural network representing the function·(-1)for each(i,j)∈E2.
It follows from Eq.(16)and proposition 2 that

for all(λk1,λk2,...,λkN)∈{-1,1}N.
Now,we have constructed an NNQWFΨS,Ω(λk1,λk2,...,λkN)satisfying Eq.(17). This leads to the following conclusion.
Theorem 1 Any digraph state|-→G〉can be represented as a spin-zNNQS (7) generated by a neuron network with|E|+|E2∖E3|hidden neurons.
If we identity an undigraphG=(V,E) with the digraph-→G=(V,-→E)in such a way that-→E={(i,j):(i,j)∈E},then the states|G〉and|-→G〉are equal and|E2∖E3|=0. With this observation,we have the following corollary.
Corollary 1 Any(undirected)graph state|G〉can be represented as a spin-zNNQS(7)generated by a neuron network with|E|hidden neurons.
Example 1 Consider a digraph-→G= (V,-→E) withV={1,2,...,8}and-→E={(1,2),(1,3),(3,1),(3,4),(4,6),(7,4),(7,5),(6,8),(8,6)}, which is represented on the left side of Fig. 14. In this case, the wave function of the digraph state|-→G〉reads

In the middle of Fig.14,we demonstrate the idea of constructing a neural network representation of digraph state|G〉. The neural network that generatesΨG(λk1,...,λk8)is given on the right side of Fig.14.

Fig.14. Neural network representation of digraph states. The first figure is graph representation of a digraph state. The second one is an idea of the process. The third one is neural network representation of the digraph state,where ω =-π i/4,Si=σzi,i=1,...,8.
In this case,the parameters are

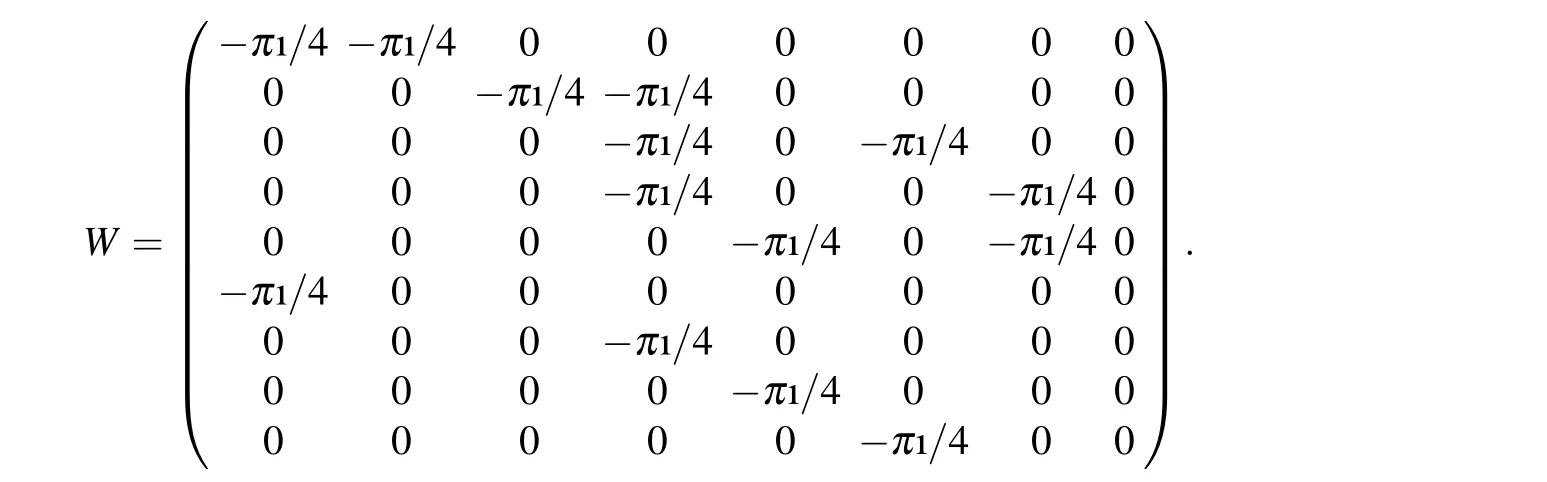
5. Conclusion
In summary,we have introduced digraph states and constructed explicitly neural network representations for any digraph state. This means that we have found a new class of entangled multipartite quantum states that can be learned with neural network. Our method shows constructively that all digraph states can be represented precisely by proper neural networks proposed in Ref.[30]and mathematically formulated in Ref.[47]. The obtained results will provide a theoretical foundation for solving the quantum many-body problem with machine learning method whenever the wave-function is known as an unknown digraph state or it can be approximated by digraph states.
Acknowledgements
The authors would like to thank the anonymous referees for their kind comments and suggestions.
This work was supported by the National Natural Science Foundation of China (Grant Nos. 12001480 and 11871318),the Applied Basic Research Program of Shanxi Province(Grant Nos. 201901D211461 and 201901D211462), the Scientific and Technologial Innovation Programs of Higher Education Institutions in Shanxi (Grant No. 2020L0554), the Excellent Doctoral Research Project of Shanxi Province(Grant No. QZX-2020001), and the PhD Start-up Project of Yuncheng University(Grant No.YQ-2019021).
- Chinese Physics B的其它文章
- Ergodic stationary distribution of a stochastic rumor propagation model with general incidence function
- Most probable transition paths in eutrophicated lake ecosystem under Gaussian white noise and periodic force
- Local sum uncertainty relations for angular momentum operators of bipartite permutation symmetric systems
- Quantum algorithm for neighborhood preserving embedding
- Vortex chains induced by anisotropic spin–orbit coupling and magnetic field in spin-2 Bose–Einstein condensates
- Short-wave infrared continuous-variable quantum key distribution over satellite-to-submarine channels