基于光的反射与折射定律的表述方法推导及应用

周旭环，龚云辉，吴绍华,2，王元康，黄娅芳，叶洪伟，王光伟，王一成

（1.云南北方光学科技有限公司，云南 昆明 650217；2.昆明物理研究所，云南 昆明 650223；3.陆装重庆军代局驻昆地区第二军事代表室，云南 昆明 650032）

引言

几何光学以光的粒子性为基础来研究光的传播和成像问题，避免了因波面研究带来的计算和处理上的困难，其在光学仪器理论研究中有很大的实际意义。几何光学通过简化，把光能的传播和光学成像归结为光线的传播，并且遵循直线传播定律、独立传播定律、反射定律、折射定律[1]。不论是平面镜、透镜还是棱镜，在其设计、制造、检验过程中都需要考虑光的反射与折射。因此，光的反射和折射是光学应用中最基本的方法和出发点。

随着数学工具的发展，光的反射和折射的表述方法除了传统表述方法外，还发展出了矢量表述、矩阵表述、四元数表述方法。在4种表述方法中，传统表述方法简洁明了，但不易反映光线在三维空间的传播规律；矢量表述方法物理意义清晰，但不便于计算，尤其不适合用计算机进行计算[2]；矩阵表述方法解决几何光学问题简洁方便，也便于计算机进行运算[3]；四元数表述方法与矩阵表述相比，其几何意义明确，计算更简单[4]。人们利用反射定律和折射定律的矢量表述、矩阵表述、四元数表述方法对棱镜的误差分析、可逆性研究、棱镜装调等进行了研讨[5-8]，说明几种表述方法均是处理光学应用问题的有效工具。

本文首先对光的反射与折射的4种表述方法进行了介绍与推导；然后通过对施密特棱镜检验光路的计算，验证了反射定律的矩阵表述与四元数表述方法；最后给出了Matlab编制的计算程序，为棱镜误差分析、棱镜胶合、棱镜调整等应用提供了理论参考。

1 光的反射与折射的传统表述方法

1.1 光的反射

如图1所示，入射光线、反射光线和法线在同一平面内，且入射光线和反射光线位于法线的两侧，与法线的夹角大小相等。

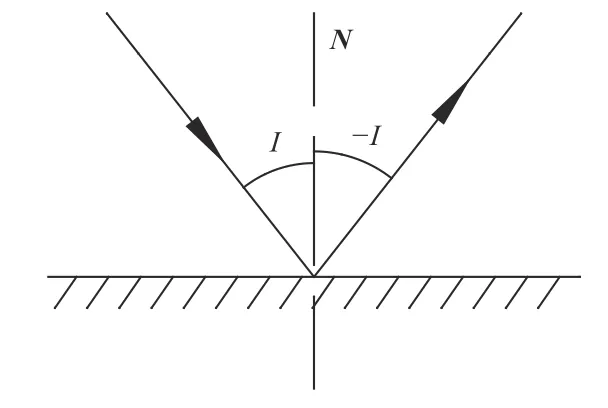
图1 光的反射图Fig.1 Reflection diagram of light

为使各参量具有确切的含义，本文采用如下符号规则。光线与法线的夹角：当法线沿逆时针方向旋转一个锐角能与光线重合时，该角度取正值；反之为负值。图1中，入射光线与法线的夹角为正值；反射光线与法线的夹角为负值。

1.2 光的折射

如图2所示，入射光线、折射光线和法线在同一平面内；折射光线和入射光线位于法线的两侧；入射角的正弦跟折射角的正弦的比值与入射角的大小无关，等于后一介质与前一介质的折射率之比，即：

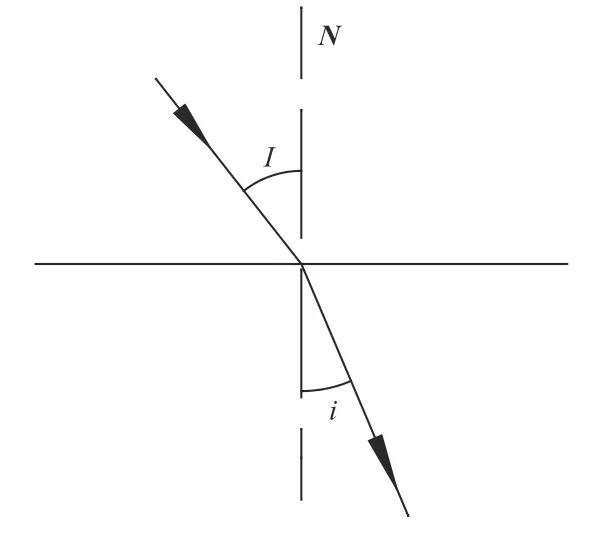
图2 光的折射图Fig.2 Refraction diagram of light

光的反射定律和折射定律可以由费马原理和惠更斯原理2种方法证明[9]。

2 光的反射与折射的矢量、矩阵及四元数推导

2.1 光的反射矢量

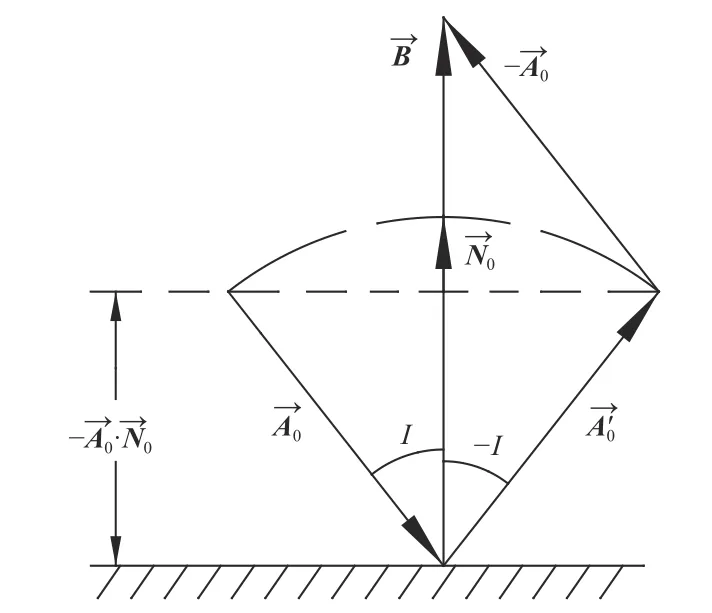
图3 反射定律的矢量表述图Fig.3 Vector expression diagram of law of reflection

由（2）式和（3）式可得：

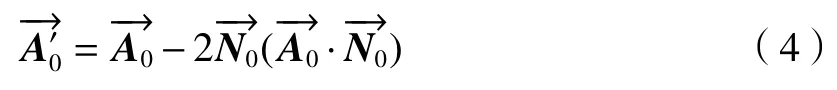
以上即为光反射定律的矢量表述。

2.2 光的折射矢量

如图4所示，光线入射角为I，折射角为i，入射光所在空间的折射率为n，折射光所在空间的折射率为 n′，由（1）式可得：

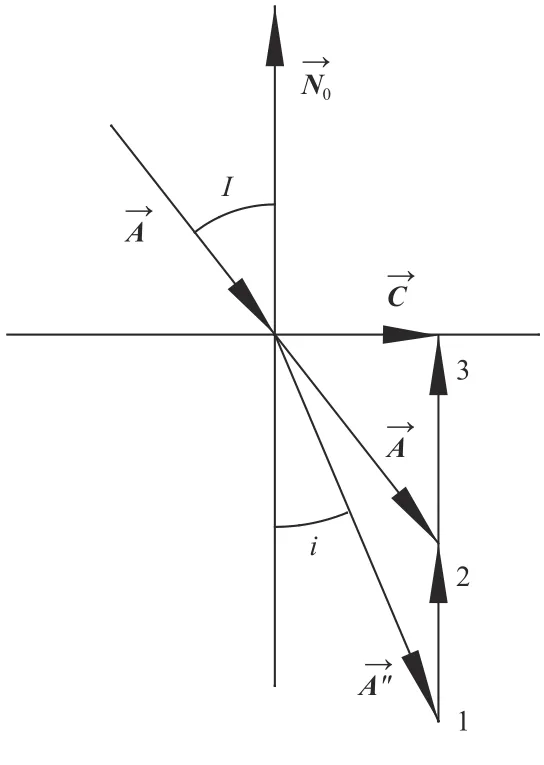
图4 折射定律的矢量表述图Fig.4 Vector expression diagram of law of refraction

如果用矢量分别表示入射光线、法线、反射光线的单位矢量，则（5）式可以写为

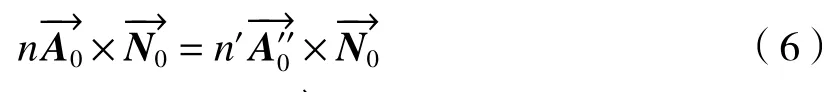
由（3）式可得：

将（10）式、（11）式代入（9）式得：

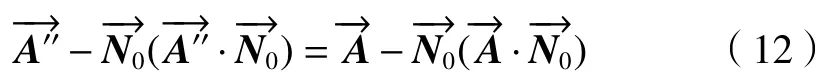
式中：

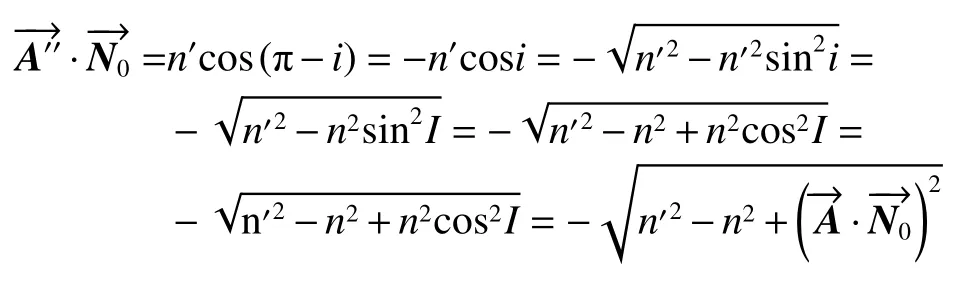
则：

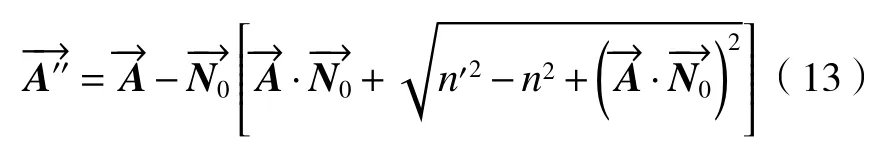
以上即为光折射定律的矢量表述。

2.3 光的反射与折射的矩阵推导

2.3.1 光的反射矩阵

建立空间坐标系，并令

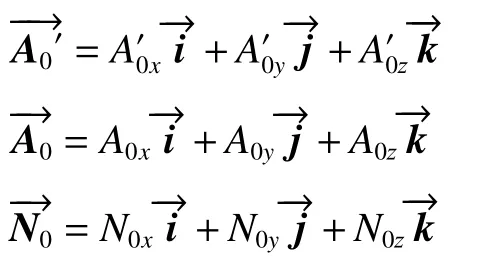
将上式带入（4）式可得：

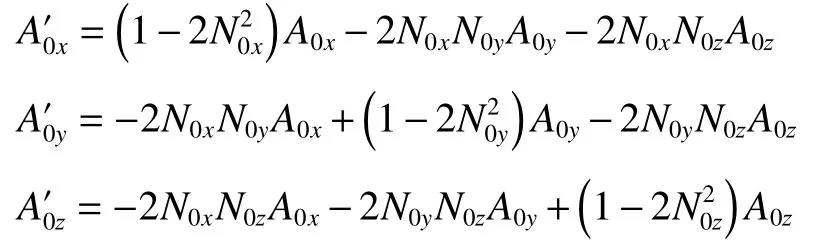
写成矩阵形式则有：

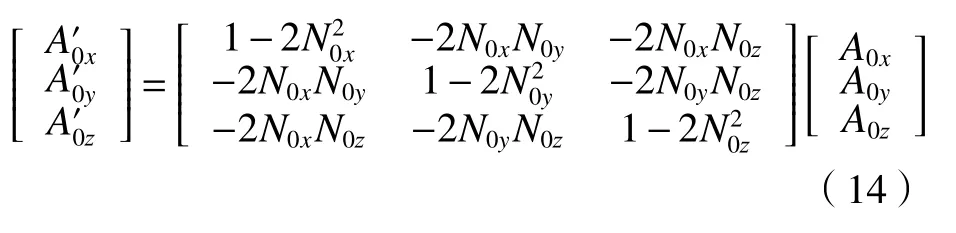
令

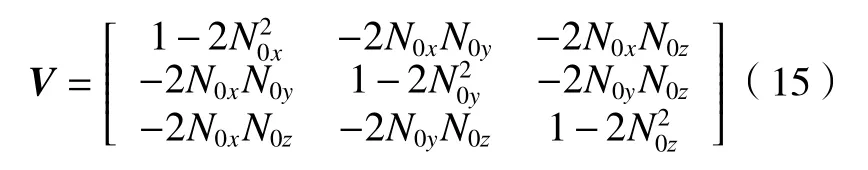
则（14）式可写为

以上即为反射定律的矩阵表述。

2.3.2 光的折射矩阵

由于光的折射并不是线性变换，因而严格的折射定律并不能用（14）式的形式来描述。但是引入入射角I和折射角i后，在球面折射系统中可以用矩阵形式来描述折射。如图5所示，光线AP透射到球面上的P点。光线AP的状态参量为( y，nsinα)，折射后的光线状态参量为 (y′，n′sinβ)。光线与光轴夹角的符号规则为：当光轴沿逆时针方向旋转一个锐角能与光线重合时，该角度取正值；反之为负值，则图5中的α 、I、i 为 正值； β 、φ为负值。图5中的y和R取正值。

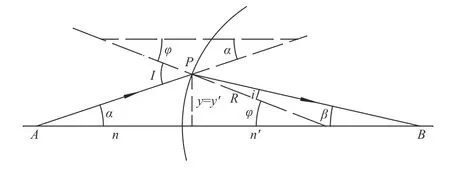
图5 球面的折射图Fig.5 Refraction diagram of spherical surface

由图有：

则：

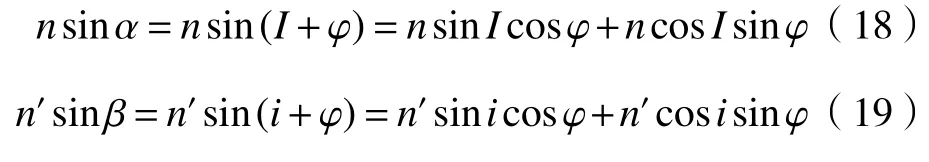
又由折射定律有：

由（17）式～（20）式可得：

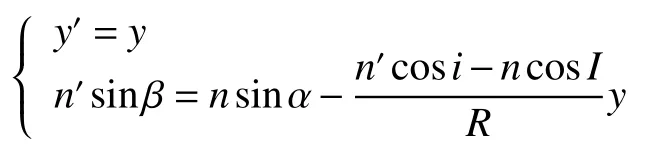
写成矩阵形式则为

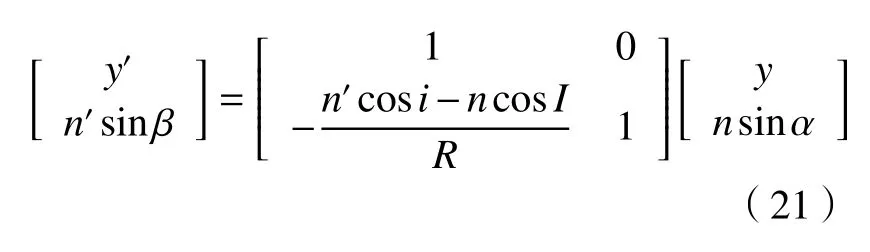
在近轴近似下，光线与光学系统中心轴的夹角α很小，可以有近似关系 sinα=tanα≈α ，cosα≈1。此种情况下，光学系统变换退化为线性变换。则（21）式可简化为

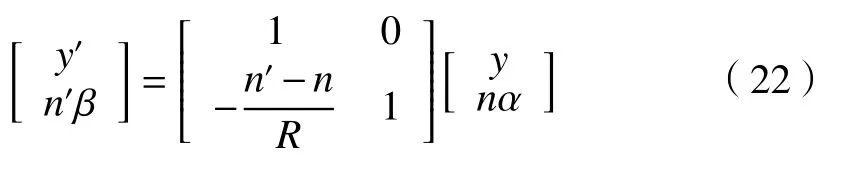
近轴矩阵方法可以很好地描述高斯光学中的相关问题，也便于计算机计算，是处理几何光学中光学系统成像的有效工具。

2.4 光的反射与折射的四元数表述

2.4.1 四元数

四元数于1843年由哈密顿（Hamilton）建立，但其直到刚体动力学理论发展后才得到人们重视，并成为一个广泛的科学项目[10-13]。现在，其在计算机图形学、刚体姿态控制、偏振光学、光电侦查等领域已得到广泛应用[14-16]。

四元数由1个实数单位和3个虚数单位i、j、k 组成，可以写成如下形式：

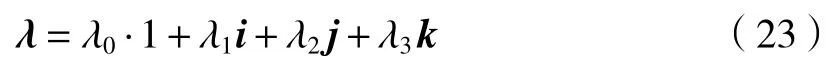
式中：λ0、λ1、λ2、λ3均 为实数，i、j、k 服从以下运算规律：

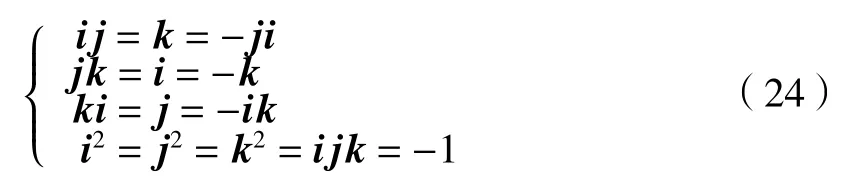
四元数 λ 的共轭 λ*为

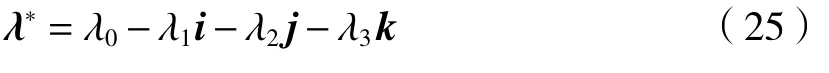
四元数的模为

四元数的逆为

任取2个四元数：

P=p0+p1i+p2j+p3k

Q=q0+q1i+q2j+q3k

四元数的加法为

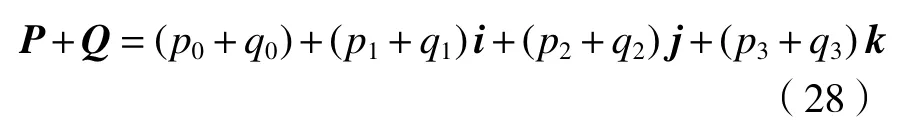
令P=p0+p，Q =q0+q, 四元数的乘法（为区别于矢量的点乘和叉乘，这里我们称四元数的乘法为直乘）可表示为

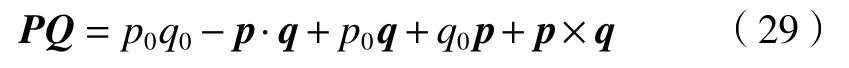
四元数乘法满足结合律和分配律，但一般不满足交换律。

当 p0=0，q0=0时 ，P=p，Q =q，称此种四元数P与 Q为纯四元数。因为纯四元数仅由虚部的3D矢量决定，可以将任意的3D矢量表示为纯四元数。当2个纯四元数直乘时，（29）式变为

考虑三维矢量的旋转，如图6所示，矢量为

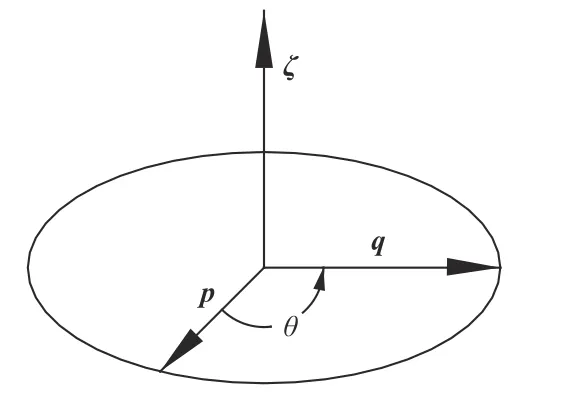
图6 三维矢量旋转图Fig.6 Rotation diagram of 3D vector

p=p1i+p2j+p3k

q=q1i+q2j+q3k

且 |p|=pλ，|q|=qλ，pλ=qλ，p与 q之间的夹角为θ，单位矢量 ζ 垂直于 p与 q所在的平面。则由（30）式可得：

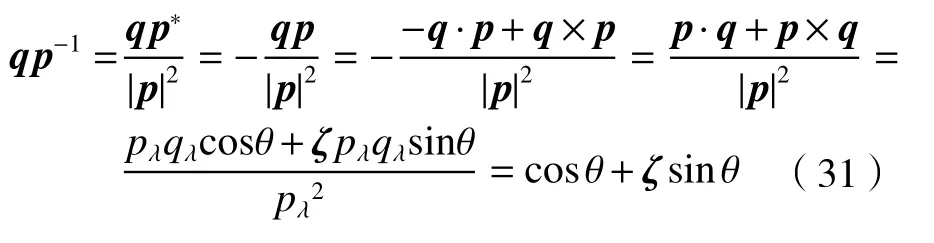
由（31）式两边直乘 p 得：

由此可以看出，形如 E=cosθ+ζsinθ的四元数表示将垂直于转轴 ζ 的矢量 p按右手螺旋方向转过θ角，从而得到矢量q。

对于更一般的情况，非实数四元数 P=p0+p ，其绕转轴ζ 旋转θ角得到 Q[10]，则：

2.4.2 光的反射四元数

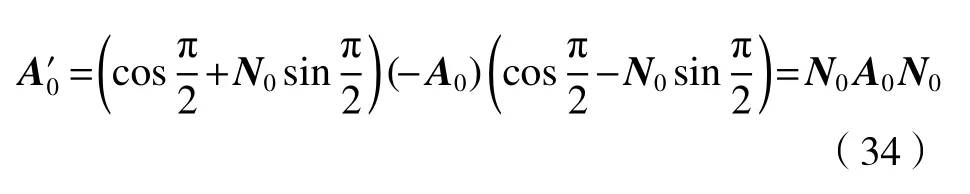
2.4.3 光的折射四元数

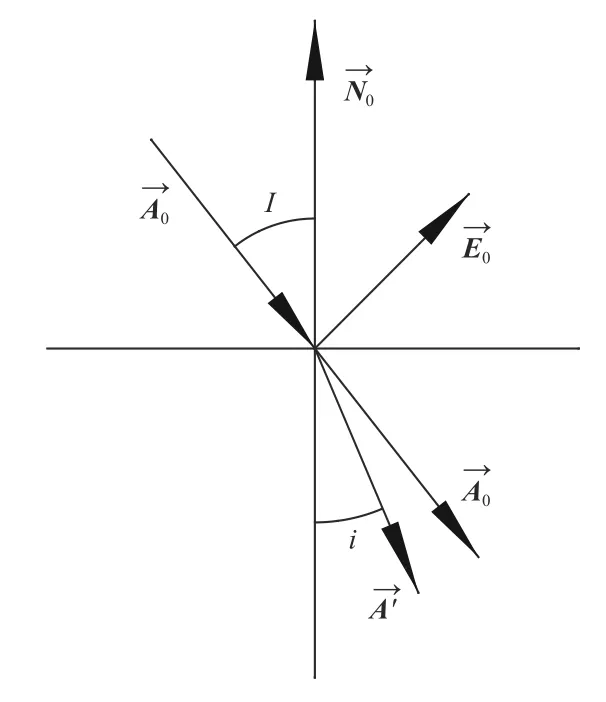
图7 折射光旋转图Fig.7 Rotation diagram of refracted light

单位矢量 E0为

或由（32）式可得：

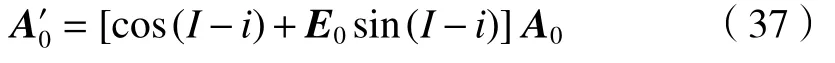
3 实验结果与分析

对其中光反射的矩阵形式与四元数形式进行验证。以施密特棱镜为例，如图8所示，入射光线由位置Ⅰ进入施密特棱镜后依次经过的反射面为2面、3面、1面、2面、1面、3面、2面；入射光线由位置Ⅱ进入施密特棱镜后依次经过的反射面为3面、2面、3面。设施密特棱镜内部的入射光为出射光为，只要计算结果满足则说明表达形式正确。

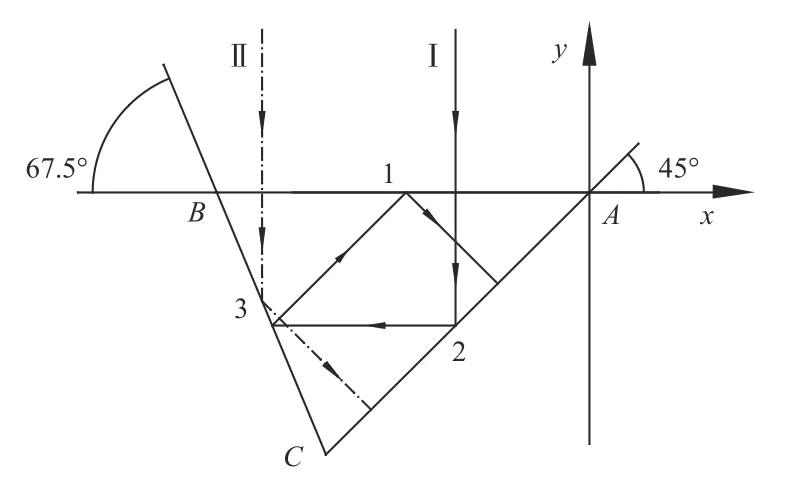
图8 施密特棱镜平行差检测光路图Fig.8 Optical path diagram of parallel error detection by Schmidt prism

由图8所示，入射光线矢量为 A0=[0-10]，1、2、3面法线矢量分别为 N1=[0-10]，N2=为提高计算速度，使用Matlab代替手动计算。

使用矢量形式计算后，算法流程如图9所示，由位置Ⅰ入射后得到反射光为 Ap7=[010]，由位置Ⅱ入射后得到反射光为 Ap3=[010]。Ap3=Ap7=-A0，说明光反射的矢量形式正确。

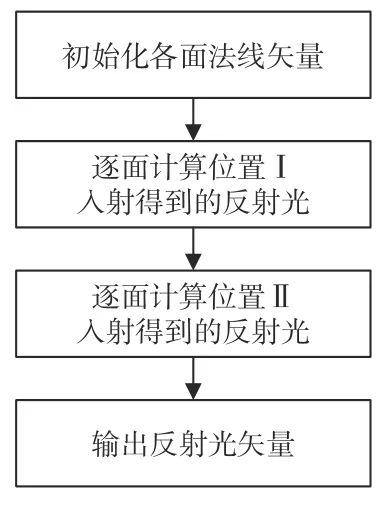
图9 矢量形式算法流程图Fig.9 Flow chart of vector form algorithm

使用矩阵形式计算后，算法流程如图10所示。由位置Ⅰ入射后得到反射光为 Ap7=[010]，由位置Ⅱ入射后得到反射光为 Ap3=[010]。Ap3=Ap7=-A0，说明光反射的矩阵形式正确。

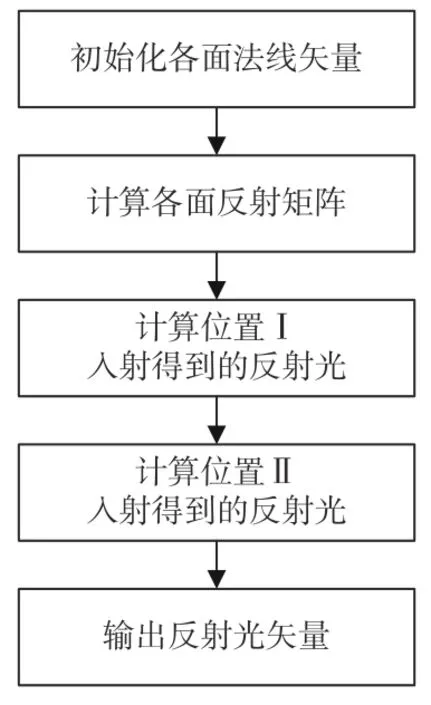
图10 矩阵形式算法流程图Fig.10 Flow chart of matrix form algorithm

使用四元数形式计算后，算法流程如图11所示。由位置Ⅰ入射后得到反射光为 Ap7=[0010]，由位置Ⅱ入射后得到反射光为 Ap3=[0010]。Ap3=Ap7=-A0，说明光反射的四元数形式正确。

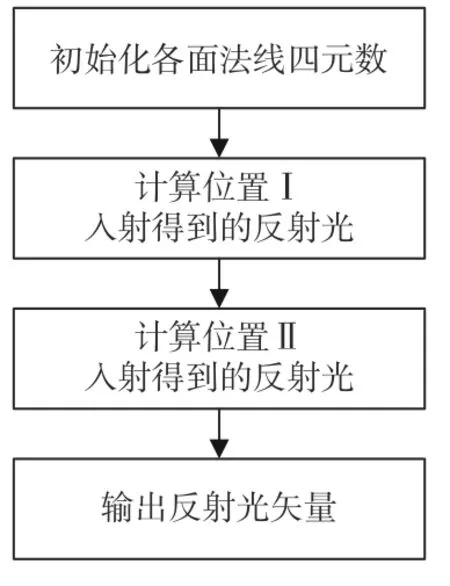
图11 四元数形式算法流程图Fig.11 Flow chart of quaternion form algorithm

4 验证及应用

在施密特棱镜的实际生产过程中，由于存在制造误差，往往会观察到3个反射像，如图12所示。

1面反射的光线对应的十字线为 Ap，从位置Ⅰ入射得到的反射光对应的十字线为 A1，从位置Ⅱ入射得到的反射光对应的十字线为 A2。图中十字线水平方向的距离与施密特棱镜的第一平行差对应。由图12可以看出，A1与 A2在水平方向上对称分布于 Ap两侧。

图12 施密特棱镜平行差 实际检测结果图Fig.12 Diagram of actual detection results of parallel error of Schmidt prism

现用光反射的四元数形式对该现象做一个证明。

首先考虑单个平面的角量误差。如图13所示，平面a的法线为，转动 θ 角度后法线为。

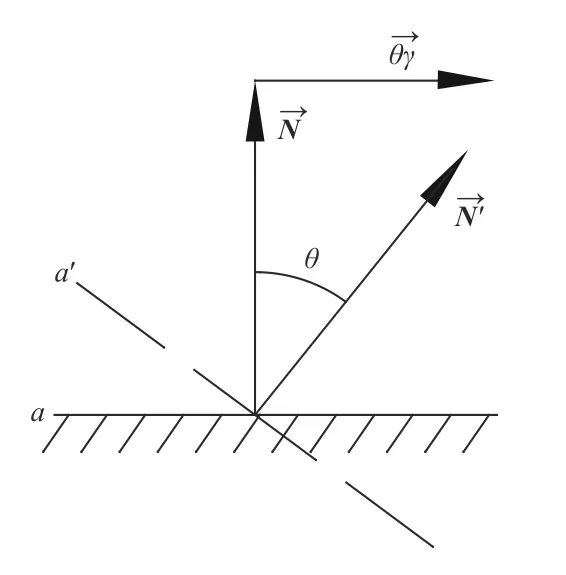
图13 单个平面微量转角图Fig.13 Micro angle of single plane

设单位矢量 ζ 垂直于N和N′组成的平面（垂直于纸面向里），则由（30）式可得：

由于θ 角为小量，则上式变为

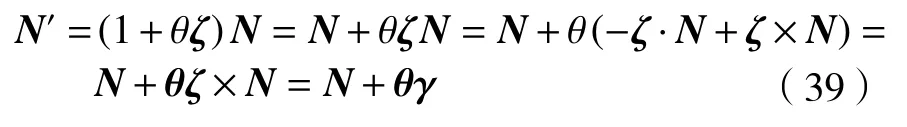
式中：γ 为位于N和N′组成的平面内且平行于平面a的单位矢量。

由于第一平行差只与光轴截面内角度误差有关[17]，假设2面在光轴截面内的角度误差为 θ2，3面在光轴截面内的角度误差为 θ3，取三角形内角角度增大的方向为正，则 γ2、 γ3为

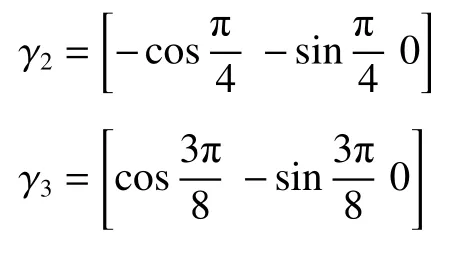
2面、3面的法线矢量为

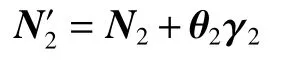
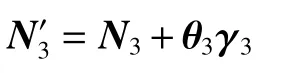
对棱镜内部出射前的反射光线进行计算，算法流程如图14所示。

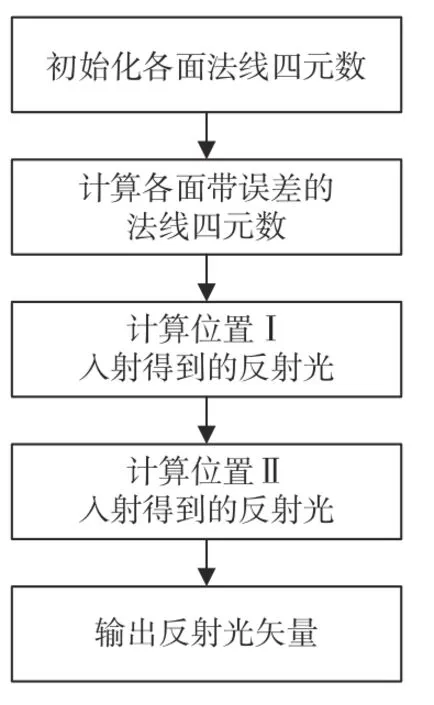
图14 棱镜内部出射前的反射光线算法流程图Fig.14 Flow chart of reflected light algorithm before prism exit

得到的结果为

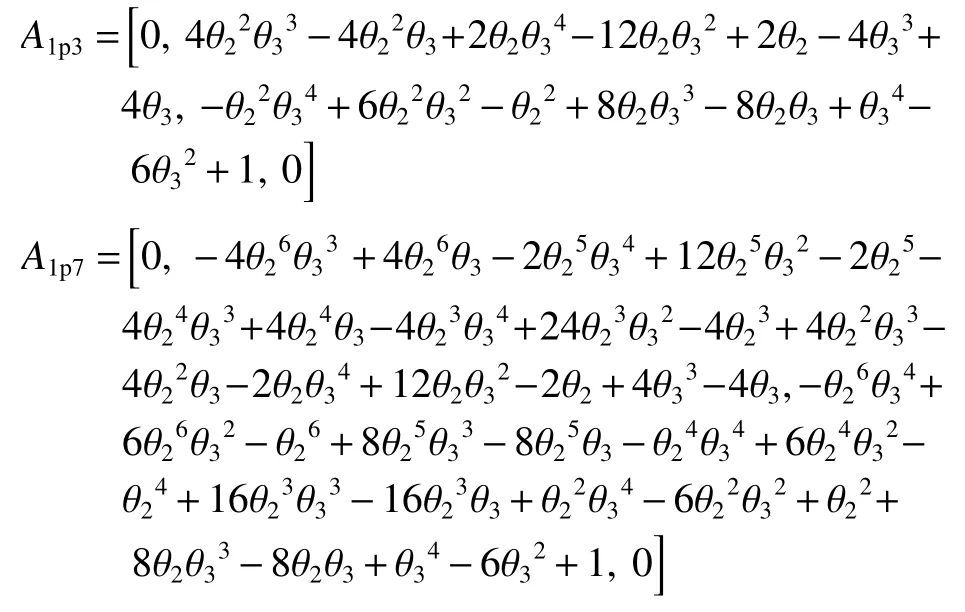
略去二阶小量得到 A1p3=[0,2θ2+4θ3,1,0]，A1p7=[0,-2θ2-4θ3,1,0]，即由位置Ⅰ入射后得到的反射光为

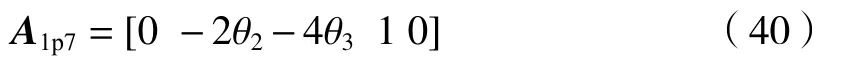
由位置Ⅱ入射后得到的反射光为

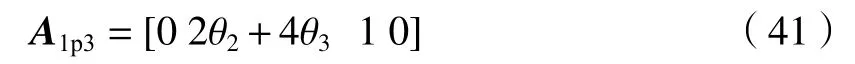
而1面的反射光为 Ap=[0010]，由上可知A1p7、 A1p3在出射前在x轴方向（水平方向）上对称分布于 Ap两侧。再由（1）式可知，A1p7、 A1p3在经过界面1折射后的出射光 A1与 A2在水平方向上对称分布于 Ap两侧。计算结果与观察结果一致。

另外由（40）式可知，施密特棱镜的第一平行差为

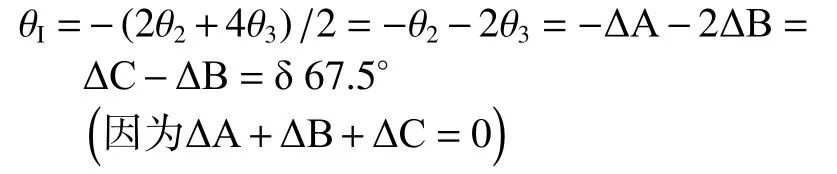
该结果与文献[17]的结论一致。

5 结论

光的反射和折射定律的传统表述方法是平面镜、透镜应用最常用的基本方法。而在光学棱镜的设计、加工和检验过程中，使用传统光的反射与光的折射及其相关表述方法对棱镜误差分析、棱镜胶合、棱镜调整等应用存在定量计算复杂、计算量大等缺点。通过对光的反射定律和折射定律不同表述方法的推导和拟合，提出了更简洁的四元数表述方法，给出了3种表述方法的Matlab计算程序，以施密特棱镜和四元数表述方法为例，使用Matlab软件详细地计算了施密特棱镜平行差检测光路。计算结果与施密特棱镜的平行差检测光路的检测结果完全一致。求出了平行差与各角度误差的关系，阐述了光学棱镜在检测图像中3个像的相互关系，为解决平行差和角度误差的关系提供了新的解决思路和方法，对光学棱镜加工和检测、误差控制、平行差精度控制具有指导性的实际应用价值。例如矢量表述方法可应用于角锥棱镜的误差分析以及转镜的反射光矢量分析；矩阵表述方法可应用于光路的可逆性分析研究；四元数表述方法可应用于别汉棱镜的消旋误差模型建模等。结合生产过程中光学棱镜加工和检测的实际应用，验证了四元数方法在棱镜角度误差分析中的准确性、有效性和实用性。