多段线缆驱动连续型空间机械臂建模与控制
丁 萌,余 鑫,武海雷,郭 毓,郭 健
(1.南京理工大学 自动化学院,江苏 南京 210094;2.上海航天技术研究所,上海 201109)
随着人类对太空的不断探索,机器人在空间任务中扮演着越来越重要的角色,例如空间站的维护与检修、太阳帆板的辅助展开、航天器燃料加注等[1]。但是在复杂狭小的空间舱内执行航天器的维修、检测等任务,要求空间服务机器人不仅具备穿越狭窄环境、自主避障的能力,同时还需具有足够灵巧的操作能力。一种能依靠自身弹性变形并可连续弯曲运动的连续型机械臂正是能实现上述目标的方案之一[2,3]。
近年来,连续型机械臂系统的动力学建模以及控制问题,吸引了国内外众多学者的关注。文献[4,5]基于Cosserat杆理论对肌腱驱动与气、液压驱动的连续型机械臂进行动力学建模,能有效模拟弹性杆形变情况下的线性与非线性行为,但求解过程十分耗时,难以满足实时控制的要求。文献[6]基于虚功原理,同时考虑摩擦效应,建立了一类绳索驱动连续型机械臂动力学模型,但其绳-盘间的接触力与绳缆张力需用迭代求解器同时求解,机械臂节段越多,其求解对计算器性能要求越高,实际应用受到一定限制。基于集中参数建模方法所建的动力学模型具有简单的特点,便于设计控制器,但存在模型描述不精确的问题。文献[7]基于Hamilton方法建立了平面绳索驱动连续型机械臂系统动力学模型,文献[8]基于欧拉-拉格朗日建模方法对单段肌腱驱动连续型机械臂建立了解析动力学模型。为建立柔体结构的简化数学模型,部分学者基于刚体等效思想,将连续型机械臂的柔性构架等效成柔性关节连接的刚性连杆,以描述机械臂形态[9]。在线缆驱动连续型机械臂的动力学建模方面虽然已有一些研究成果,但对于存在强耦合效应的多段线缆驱动连续型机械臂,还需对其动力学建模方法开展进一步研究,使其既能保证模型计算效率和精度,同时又能便于控制器设计。
连续型机械臂系统具有高度非线性、多变量强耦合等特点,这使其控制变得十分复杂。针对机械臂柔性结构特征开展具有强鲁棒性和抗干扰能力的控制方法研究,受到国内外学者们的关注。文献[2]针对线缆驱动连续型机械臂,设计了比例-微分(Proportional-differential,PD)控制器,但系统的控制性能易受系统中不确定性干扰因素的影响。Kapadia等[10]针对气动型Octarm机械臂设计了滑模变结构控制器,其系统误差收敛性能优于PD控制器,但模型参数的不确定性对控制性能影响较大。Qi等[11]针对连续型机械臂的轨迹跟踪,设计了一种模糊控制器,具有良好的稳定性与抗干扰能力,但因被控对象的高度复杂性和不确定性,难以实现精确且快速的轨迹跟踪。综上,针对连续型机械臂控制的研究取得了较大进展,但对闭环系统误差收敛的快速性研究尚少,现有控制算法尚难以使系统同时满足强抗扰能力与快速精确跟踪的控制要求。此外,在现代航天任务中,为保证航天器的快速姿态大角度机动并抑制挠性附件振动,已有部分学者将有限时间控制算法运用其中[12]。
本文针对一种带有弹性中心杆的新型多段线缆驱动连续型机械臂系统,研究其建模与控制问题。为保证模型计算效率和精度,对连续型机械臂模型进行刚体等效简化,结合欧拉-拉格朗日建模方法建立了多段线缆驱动连续型机械臂动力学模型。在此基础上,同时考虑系统存在外部时变干扰与参数不确定性,设计了一种基于非奇异终端滑模有限时间控制(Nonsingular terminal sliding mode finite-time control,NTSMFC)的连续型机械臂控制方法,以提高闭环控制系统误差的快速收敛性和干扰抑制能力。
1 线缆驱动连续型机械臂结构
本文对一种多段线缆驱动连续型机械臂展开研究,其结构如图1所示。此时机械臂为2段式结构,每节由3根线缆驱动,拉动驱动线缆可使中心弹性杆弯曲变形,间隔盘提供弯曲形状的刚度支撑。机械臂每节长度相等,均为l,各节上的支撑间隔盘等距分布。

图1 线缆驱动连续型机械臂示意图
第2节的驱动线缆通过所有间隔盘后固结于末端盘上。第1节机械臂的间隔盘上均匀分布6个驱动线缆孔和1个中心弹性杆孔,第2节机械臂的间隔盘上均匀分布3个驱动线缆孔和1个中心弹性杆,示意图如图2所示,圆孔编号ni(n=1,2;i=1,2,…,6)表示第n节机械臂的第i根驱动线缆穿过该孔,所有线缆孔与中心孔之间的中心距r相等。依此类推,通过串联若干节,便可得到更多自由度的连续型机器人,以适应实际环境操作要求,增加末端的灵活性。
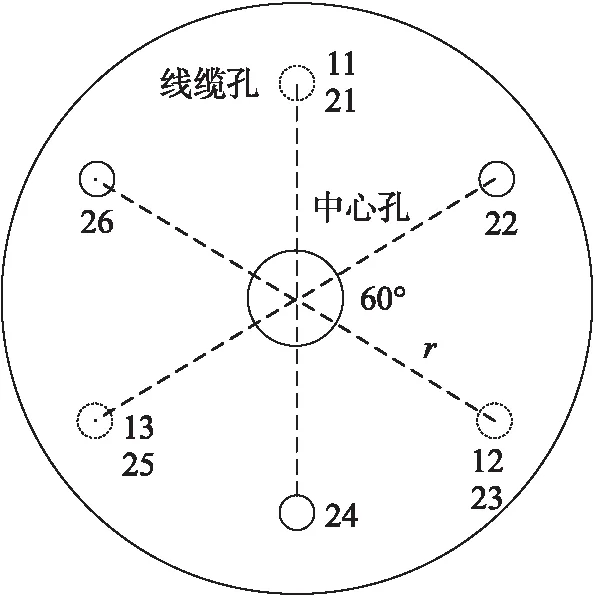
图2 间隔盘示意图
2 连续型机械臂运动学分析
2.1 假设条件
为建立图1所示多段线缆驱动连续型机械臂的数学模型,对系统做以下假设:
假设1机械臂中心弹性杆的轴向刚度远大于其弯曲刚度,忽略其轴向拉伸,并且中心弹性杆的变形为等曲率弯曲的光滑连续曲线,可近似为欧拉伯努利梁[13]。
假设2机械臂各支撑间隔盘间距小,机械臂弯曲时各驱动线缆为等曲率的连续光滑曲线,也是基于常曲率假设。
假设3中心弹性杆和驱动线缆总是垂直于基座盘、间隔盘和末端盘。
假设4考虑太空处于微重力环境,且机械臂的重力势能远小于弹性势能,忽略重力势能影响。
假设5机械臂的间隔盘薄并且属于刚性材料,忽略中心杆、驱动绳与间隔盘之间的摩擦力。
2.2 多段连续型机械臂运动学分析
假设多段连续型机械臂由N节构成,且每节上有K个间隔盘,每节首、末支撑盘中心点固连基坐标系与末端坐标系,基坐标系由On-1-Xn-1Yn-1Zn-1(n=1,2,…,N+1)表示,末端坐标系由On-XnYnZn(n=1,2,…,N)表示。图3为连续型机械臂第n节弯曲时的几何模型,机械臂弯曲平面坐标系Orn-XrnYrnZrn为由基座标On-1-Xn-1Yn-1Zn-1绕Zn-1轴旋转γn角所得,βn表示机械臂末端弯曲角度,则N段连续型机械臂姿态角φ表示为φ=[β1γ1β2γ2…βNγN]T。通过驱动线缆控制机械臂弯曲使连续型机械臂到达指定位姿状态,对于该机械臂的运动学分析,包括驱动空间与关节空间的相互映射,以及关节空间与任务空间的相互映射。
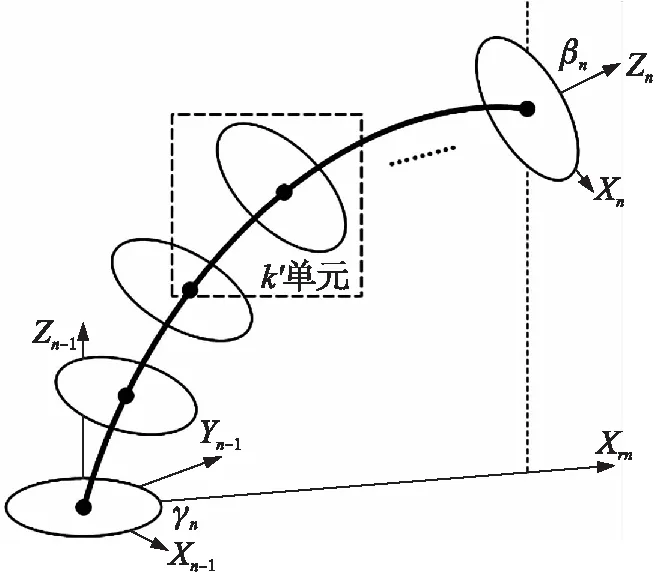
图3 机械臂第n节几何模型图
多段连续型机械臂从关节空间到任务空间的正运动学分析,即为由关节空间中的姿态角变量βn(n=1,2,…,N)与γn(n=1,2,…,N)求解任务空间中机械臂的末端位姿,机械臂每节的基坐标系On-1-Xn-1Yn-1Zn-1至末端坐标系On-XnYnZn的齐次变换矩阵
(1)
N段机械臂关节空间至任务空间的运动学映射关系为
0TN=0T1·1T2,…,N-1TN
(2)
基于假设1~3,定义第n节中心弹性杆上任一点相对于机械臂基底盘坐标系O0-X0Y0Z0的位置坐标为rn0=[xnynzn1]T,相对于第n-1节的末端支撑圆盘坐标系On-1-Xn-1Yn-1Zn-1的位置坐标为rn1=[xn1yn1zn11]T
(3)
式中:sn表示第n节中心弹性杆上任一点距离首支撑盘中心点的弧长。
rn0与rn1位置坐标间的关系为
rn0=0Tn-1·rn1
(4)
机械臂运动弯曲的过程中,中心弹性杆和各驱动线缆的弯曲角度相同。由图4所示的驱动线缆几何关系,多段机械臂的驱动空间与关节空间的逆映射关系即机械臂各驱动线缆与姿态角度之间的关系为
(5)
式中:ΔLni表示连续型机械臂第n节的第i根驱动线缆长度变化,θni为第n节的第i根驱动线缆在间隔盘的分布角度。
对式(5)进行微分,可得驱动空间的运动学关系为
(6)


(7)
式中:JXφ为连续型机械臂任务空间与关节空间速度的雅可比矩阵。

图4 机械臂驱动线缆弯曲示意图
3 多段线缆驱动连续型机械臂动力 学建模分析
为建立实用型且能抑制未建模动态的动力学模型,对模型进行了刚体等效简化。如图3所示,将连续型机械臂第n节的某一刚性间隔盘与其连接的中心弹性杆划分为1个单元,k′单元上的弹性杆等效为轻质连杆,不失一般性,设定该单元的重心落在间隔盘的中心点处。基于该设定,依据式(8)所示的拉格朗日第二类方程建立该机械臂的动力学模型。
(8)
式中:Ek、Ep分别为连续型机械臂的动能与势能,Qj为其广义力方程。
(1)动能计算。
假设机械臂的中心弹性杆无扭转,即不产生转动动能,只考虑驱动线缆、中心弹性杆与间隔盘的平动动能,机械臂每节动能为各单元的动能之和。定义sk′为各节上第k′个单元质心点处的弧长,其表达式为
(9)
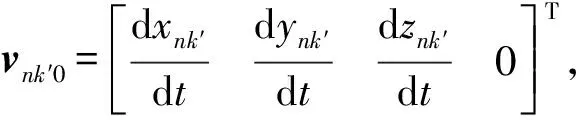
(10)
mnk′=m0+mp+3·(N-n+1)·mc
(11)
式中:mnk′表示第n节上第k′个单元的总质量,m0、mp、mc分别表示单元的中心弹性杆、间隔盘以及驱动线缆的质量。
由式(10)、(11),得到整个多段线缆驱动连续型机械臂上的动能方程
(12)
式中:M∈R2N×2N是1个对称正定矩阵。
(2)势能计算。
根据假设4,忽略机械臂的重力势能,仅考虑其弹性势能。第n节上的弹性势能为
(13)
式中:E1和E2分别为弹性杆和驱动线缆的弹性模量,I1、I2分别为弹性杆和驱动线缆的惯性矩。
多段线缆驱动连续型机械臂的总势能
(14)
(3)广义力计算。
考虑假设5,依据达朗贝尔原理,多段线缆驱动连续型机械臂的广义力为[15]
(15)
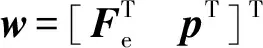
将动能、势能以及广义力表达式(12)、(14)、(15)代入式(8),得到多段线缆驱动连续型机械臂的动力学方程为
(16)
由式(16),多段线缆驱动连续型机械臂动力学模型表示为
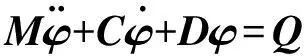
(17)

(18)
(19)
4 多段线缆驱动连续型机械臂姿态 控制
针对多段线缆驱动连续型机械臂的快速姿态稳定控制问题,考虑系统存在外部时变干扰与参数不确定性,研究基于非奇异终端滑模的有限时间控制。
4.1 非奇异终端滑模有限时间控制律设计
考虑外界时变干扰与系统参数不确定性且末端未施加外力的情况,连续型机械臂的动力学模型式(17)可以写为
(20)
式中:JLφ为机械臂驱动空间与关节空间速度的雅可比矩阵,d(t)为系统外界时变干扰和参数不确定性总和。
假设6在多段线缆驱动连续型机械臂模型式(20)中,d(t)满足‖d(t)‖≤dH,dH>0。
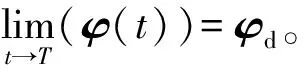
定义姿态角误差e=φd-φ,令系统非奇异终端滑模面

(21)
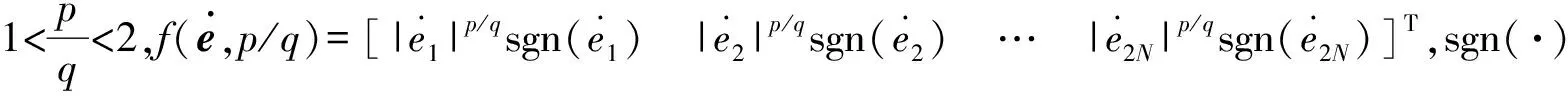
式(21)对时间t求导可得
(22)
根据滑模等效控制原理,设计非奇异终端滑模控制律为
F=Feq+Fn
(23)
(24)
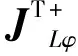
再设计切换控制项为
(25)
式中:η、k为控制增益并满足η>0,k>0。
4.2 稳定性分析
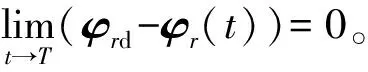
证明:
首先设计Lyapunov函数为
(26)
对时间求导可得
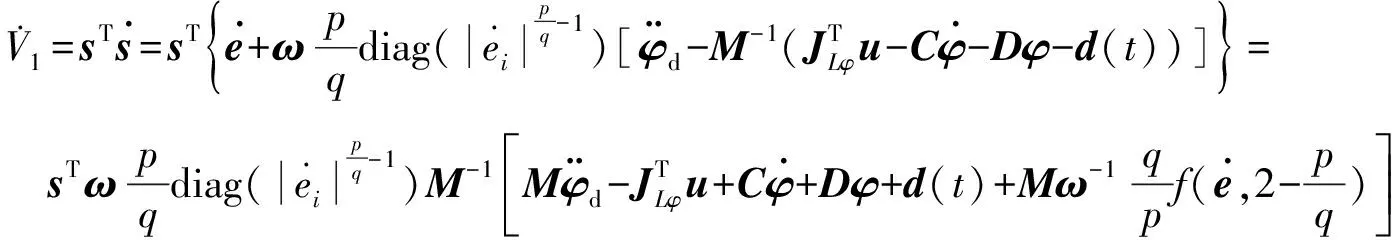
(27)
将所设计控制律式(23)代入式(27)中,并考虑假设6,可以得到
(28)
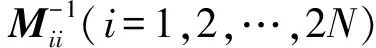

收敛时间t1满足
(29)
式中:V1(0)为V1在t=0时刻的值。
为分析系统状态到达滑模面后,系统误差的有限时间收敛性,设计Lyapunov函数为
(30)
对时间求导可得
(31)
系统状态到达滑模面后有s=0,则根据非奇异终端滑模函数式(21)可得

(32)
即
(33)
将式(33)代入式(31)中,可得
(34)
将式(30)代入式(34)中,可得
(35)
根据式(35)可得
(36)
对式(36)积分可得收敛时间t2为
(37)
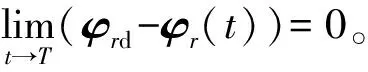
5 数值仿真与分析


由图5可知,在存在参数不确定性与外部干扰情况下,非奇异终端滑模控制器与PD控制器均能跟踪上连续型机械臂的期望姿态角,但前者能在有限时间内快速跟踪期望姿态角,PD控制器的姿态跟踪速度相对较低。由姿态角位置误差图6可知,基于非奇异终端滑模控制器的姿态角位置误差的稳态性能较好,姿态角稳态误差保持在±2×10-3rad误差带之内,收敛精度较高,而PD控制器姿态角稳态误差在±1×10-2rad误差带内,相比本文所提控制器误差精度相差1个数量级。

图5 姿态角响应曲线图
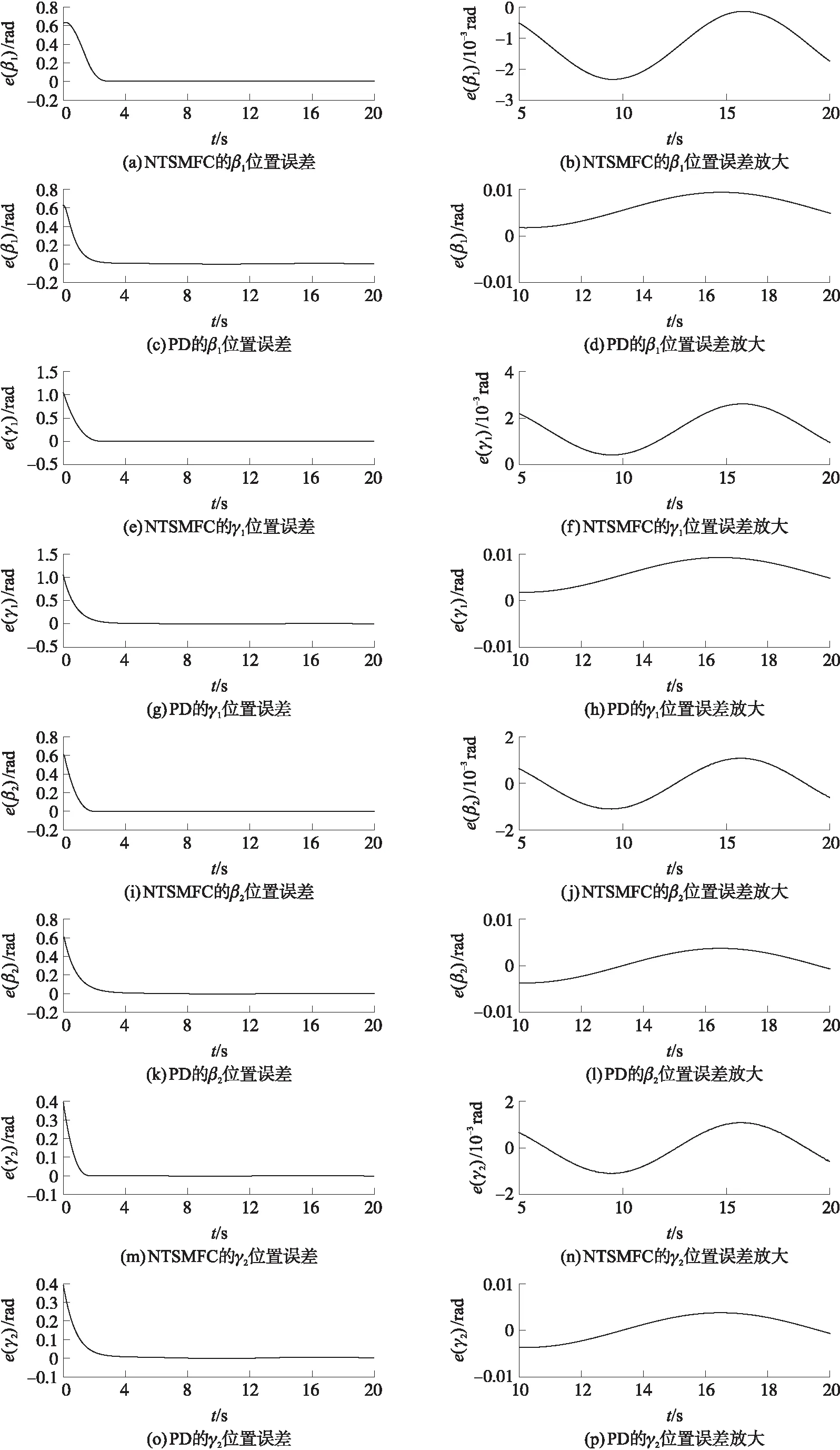
图6 NTSMFC与PD控制仿真结果图
6 结束语
本文针对一类具有柔性骨架、高自由度、强耦合的细长型结构的多段线缆驱动连续型机械臂系统,基于刚体等效建模思想对机械臂各节进行单元划分,将各单元上的中心弹性杆等效为轻质连杆,并依据欧拉-拉格朗日建模方法,建立了多段连续型机械臂动力学模型。针对系统中存在的参数不确定性与外部时变干扰,设计了一种基于非奇异终端滑模的连续型机械臂有限时间控制算法。仿真结果表明,所提控制方法提高了闭环控制系统的快速收敛性与跟踪精度。

