二阶脉冲微分方程Dirichlet边值问题解的存在性
何 婷
(西安电子科技大学 数学与统计学院, 西安 710126)
解的存在性, 其中: c∈C([0,1],), h∈C([0,1]×,), ci,hj∈, i=1,2,…,p, j=1,2,…,q; p,q∈; Dirac δ-函数为当x≠0时, δ(x)=0, δ(0)=+∞, δ(x)dx=1; 点0 考虑二阶脉冲微分方程Dirichlet边值问题 (1) 其中:c∈C([0,1],),h∈C([0,1]×,),ci,hj∈,i=1,2,…,p,j=1,2,…,q;p,q∈; Diracδ-函数为当x≠0时,δ(x)=0,δ(0)=+∞,δ(x)dx=1; 点0 |h(x,u)|≤q(x)+p(x)|u|,x∈[0,1],u∈. (2) 问题(1)在物理、 数学和工程等领域应用广泛[1-5].本文首先在条件(2)下证明问题(1)解的存在性; 其次证明问题(1)等价于 (3) 关于脉冲微分方程(3)这类方程目前已有很多研究成果[6-11].其中Liu等[6]研究了 (4) 在非线性项满足次线性、 超线性和渐近线性3种情形下解的存在性, 其中0=t0 定理1[6]假设: 1) 存在a,b>0,γ∈[0,1), 使得 2) 存在aj,bj>0,γj∈[0,1)(j=1,2,…,m), 使得 本文在f(t,u)至多线性增长的条件下讨论二阶脉冲微分方程Dirichlet边值问题(1)解的存在性. 本文总假设: (H1)c∈C[0,1]; (H2)h∈C([0,1]×,), 存在p(·),q(·)∈L2[0,1], 使得式(2)成立; 本文主要结果如下: 定理2假设(H1)~(H3)成立, 则脉冲问题(1)存在一个解u=u(x), 且满足 注1带Dirac形脉冲问题的特征可参见文献[12-13], 问题(1)这种形式有利于在泛函框架下定义弱解. 注2本文研究结果不仅得到了问题(1)解的存在性, 还确定了解的上界. 令H∶=W01,2(0,1), 问题(1)的弱解u∈H满足下列积分等式: 定义 {z1,z2,…,zr}∶={x1,x2,…,xp}∪{y1,y2,…,yq}, 1≤r≤p+q; 0=z0 令D(I)(I⊂)表示在I上带有紧支撑的无穷次可微函数全体,k∈{1,2,…,r+1}, 选择v∈D(Ik), 且延伸v(x)=0,x∈(0,1)Ik, 则v∈H.对式(5)分部积分, 有 (6) 因为对任意的v∈D(Ik), 式(6)都成立, 所以存在常数a∈, 使得 (7) 从而u∈C1(Ik).又由式(7)得 u″(x)-c(x)u(x)+h(x,u(x))=0,x∈Ik, (8) 令0<η 因为对于任意的v∈D(zk-η,zk+η), 式(9)都成立, 所以存在常数a∈, 使得 由式(10)得 Δu′(zk)∶=cku(zk)-hk. (11) 问题(1)等价于问题 (12) 带脉冲条件 Δu′(zk)=cku(zk)-hk,k=1,2,…,r. (13) 满足式(12),(13)的函数u即为脉冲问题(1)的古典解, 通过上述证明可知每个弱解都是古典解.另一方面, 每个古典解显然都是弱解. 对于任意连续函数r(x)≥0(x∈[0,1])及实数ri≥0(i=1,2,…,p), 在空间H中定义如下内积: 则范数‖u‖=(u,u)1/2.设f(x)(x∈[0,1])和fi(i=1,2,…,p)为连续函数, 定义算子F:H→H为 (14) 定义算子S:H→H为 (15) 引理1若u∈H, 则 ‖u‖L2(0,1)≤(minr(x)+π2)-1/2‖u‖. 证明: 对任意u∈H, 由文献[14]有 则 证毕. 引理2对于由式(14)定义的算子F:H→H, 有 证明: 由于u∈H,F:H→H, 所以F(u)∈H, 证毕. 引理3对于由式(15)定义的算子S:H→H, 有 证明: 由于u∈H,S:H→H, 所以S(u)∈H, 再结合条件(H2), 利用Hölder不等式和Minkowski不等式, 有 证毕. 引理4(Leray-Scauder不动点定理)[15]设E是Banach空间, 算子T:E→E全连续, 若集合 {‖x‖|x∈E,x=θTx, 0<θ<1} 有界, 则T在闭球A⊂E中必存在不动点, 其中 A={x|x∈E, ‖x‖≤R},R=sup{‖x‖|x=θTx, 0<θ<1}. 下面证明定理2.令c+和c-分别表示c(x)的正部和负部, 对应c±=max{±c(x),0}, 即c(x)=c+(x)-c-(x).则问题(1)可以改写为 (16) u=Fc-(u)+S(u) (17) 的不动点, 其中Fc-,S:H→H为全连续算子.引入 u=θ(Fc-(u)+S(u)),θ∈(0,1). (18) 设u为式(18)的解, 则根据引理2和引理3, 有 从而 令 则‖u‖C[0,1]1 引言与主要结果








2 弱解的正则性




3 引 理



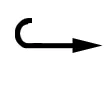
4 主要结果的证明