大规模网络中k-点连通分量发现算法研究
何瀛龙 王梦博 白雨 李源
(北方工业大学信息学院 北京市 100144)
1 引言
在大规模的网络分析中,分量检测是非常重要的问题之一。发现高度连通的分量可以帮助我们解决许多现实生活中的实际问题,例如,社会网络群体的结构凝聚力是研究社会群体凝聚力的重要的社会学指标;从城市网络中发现了凝聚子群进而研究影响因素以及措施;在信息传播中能描述出网络核心位置,有助于发现信息传播中的关键节点。
本文主要研究k-点连通分量(k-VCC),k-VCC 和社会学中的结构凝聚力概念是等价的,除此之外k-VCC 还有许多重要的特征。首先根据惠特尼定理,k-VCC 被包含在k-核(k-core)和k-边连通分量(k-ECC)之中,因此k-VCC拥有着k-core 和k-ECC 的所有结构特性,更具有凝聚力。k-VCC 允许分量之间允许重叠,在真实复杂网络中分量重叠也是重要且自然的特征。
给定图G 和一个整数k,如何计算出G 的所有k-VCCs。现有算法一般思路是,将图G 递归地划分为重叠的子图。若G 不是k-VCC,则找到一组小于k 的点割集对G 进行划分。这种自顶向下的框架的关键在于最小点割集的计算,可以转化为对局部连通度的测试,也就是判断两个顶点u,v 是否能从G 中移除最多k-1 个点使得u,v 之间不连通。局部连通度的测试利用网络流算法可以实现。而为了找到图中一组小于k 的点割集,在最坏情况下将对图G 的每对顶点都进行局部连通度的测试,若在规模较大的图中,这样做在时间上的开销是高昂的。Dong等人提出了一种减少局部连通度测试次数的优化。Li等人提出了一种基于自底向上框架的近似解。Sinkovits等人针对于k 为2 或3 的小参数设计了特殊的算法。
事实上,通过观察发现,在大规模的网络分析中,往往没有必要得到完全正确的结果,很多时候一个近似解便已经能很好的完成任务。在现有算法的框架上,本文设计了一种基于蒙特卡罗(概率采样)的近似算法,可以高效计算出所有k-VCCs,并且结合实验对误差进行了分析。
2 基本概念及相关定义
本节主要介绍一些基本概念及其符号表达,阐述了k-点连通图的相关定义,并对要解决的主要问题给出具体定义。
2.1 基本概念
本文中给定一个无向图G(V,E),V 表示图的顶点集合,E 表示图的边集合,n 表示图的顶点数即|V|,m 表示图的边数即|E|。
定义1 (点割集):对于连通图G,若V'⊆V 且G[VV']不是连通图,则V'是图G 的一个点割集。基于点割集的大小,提出了点连通度的定义。
定义2 (点连通度):图G 的点连通度定义为最小的点割集的大小,记作κ(G)。接来下给出局部点连通度的定义。
定 义3 ( 局 部 连 通 度):对 于 图G 以 及u,v∈V 满 足u ≠v,u 可达v,若V'⊆V,u,v∉V',且在G[VV']中u 和v不连通,则V'被称作u 到v 的点割集。u 到v 的最小点割集的大小被称作u 到v 的局部连通度,记作κ(u,v)。当不存在这样的点割集时κ(u,v)=+∞。局部连通度和点连通度的关系为对于所有顶点u,v∈V,κ(G)≤κ(u,v)。 接来下给出k-点连通的定义。
定义4 (k-点连通):图G 是k-点连通图如果满足条件:
(1)|V|≥k+1;
(2)图G 不存在大小为k-1 的点割集。
显然有κ(G)≥k 成立。接下来给出k-点连通分量的定义。
定义5 (k-点连通分量):图G 的子图g 是G 的k-点连通分量如果满足条件:
(1)g 是k-点连通的;
(2)不存在g 的超图是k-点连通的。
本文以k-VCC 作为缩写。
2.2 问题定义
问题1:给定一个无向图G(V,E),近似计算出它的所有k-VCCs。
3 精确算法
本节将详细介绍自顶向下检测框架,该框架的主要思想如下。如果图G 是k-点连通的,那么图G 是一个k-VCC,否则存在一个符合条件的点割集S,S 的大小小于k。在这种情况下,可以计算出这个S 并用S 对G 划分。划分的过程重复迭代进行直到剩余的每一个子图全都是k-VCC。
首先根据文献证明了这种重叠划分以及k-VCC 的数量上界为n/2,这表明这种算法是多项式时间复杂度的。
根据惠特尼定理,一个k-VCC 是必须被包含在一个k-core(图中最小度不小于k)之中的,所以在算法开始前先预先计算出k-core 以减小图的规模。
一个重要的问题是,如何计算出图G 的最小点割集。根据文献可以将问题转化为有向图上求最大流的问题。这个过程首先需要确定源点s 和汇点t,然后将原图转化为有2n 个顶点n+2m 的边且边的容量都为1 的有向流图,这样求出的最大流即κ(s,t),s 与t 的局部连通度。若对于∀s,t∈V,κ(G)=min(κ(s,t) )。根据文献可以找出图中有最小度为δ的点u,然后讨论u 不在最小点割集与在最小点割集中的两种情况,前者固定u 为源点,枚举其余顶点作为汇点即可。后者将源点和汇点在u 的邻居中两两枚举即可。
总的时间复杂度为O(n·(n+δ)·min(n,k)·m)。其中O(n)是重叠划分的次数,O(n+δ)是调用局部连通度计算的次数,O(min(n,k)·m)是计算局部连通度的时间。


4 近似算法
现有算法的瓶颈之处在于:在大规模图发现一个小于k的点割集的时间开销中非常高,根源便在于需要测试的局部连通度次数为O(n+δ),这个次数很多并且非常依赖于图的最小度,最坏情况下精确算法会退化到暴力枚举顶点对的情况。在基于现有精确算法的框架上,笔者采用蒙特卡罗的思想,对源点s 和汇点t 进行均匀采样。当采样的次数足够多时,可以发现这样的点割集的概率也就越大,后面将说明当k 与n 相差较大时,这个概率是非常优秀的。
如果图G 是一个k-VCC,则不存在小于k 的点割集,所以本节讨论如果图G 不是一个k-VCC 的情况。假设图G只有一个点割集S 大小为w 且w 定理1 单次采样中s 与t 都不属于S 的概率为:Pr(s,t∉S)=(n-w)/n。证明 令E为从V 中随机选取一个顶点的事件,E为顶点不属于S 的事件。根据条件概率公式,随机选取一个顶点不属于S 的概率为Pr(E|E)=Pr(EE)/Pr(E)。由于是本节采用均匀采样,则每个点被采样到的概率是相同的。显然E与E之间相互独立,有Pr(E|E)=Pr(E)。根据古典概率易得: (Pr(E|E)=Pr(E)=((n-w))/n (1) 单次采样中s 和t 也是相互独立的,则Pr(s,t∉S)=Pr(E|E)=(n-w)/n成立。 如果仅仅对s,t∉S 进行局部连通度测试还不能发现这个点割集w,因为可能s,t∉G[VS]中的同一连通块之中,也就是说去掉点割集S 并没有使得s,t 不连通,κ(u,v)不小于k。令E 为单次采样中,s,t∉S 且在G[VS]中s 不可达t 的事件。 定理2 单次采样中s 和t 属于G[VS]中不同连通分量的最小概率为:Pr(E)=4(n-k-1)/n。 证明 因为图G 被包含在k-core 之中,每个顶点的度数至少为k,所以去掉点割集S 后产生的最小连通分量大小为k-w+1。在最坏情况下,G[VS]只有两个连通分量设为C,C大 小分别为k-w+1 和n-k-1。令E为s 属于C的事件,E为t 属于C的事件。根据公式(2)同理可得Pr(E)=(k-w+1)/n、Pr(E)=(n-k-1)/n。因为E与E相互独立,则有: 其中C为组合数。令w=k-1,代入公式(4)即可得到公式(3)。易证,当图G 存在多个点割集或者G[VS]有多个连通分量,s,t 属于G[VS]不同连通分量的概率不会小于Pr(E)。 表1: 统计数据集 对属于G[VS]中不同连通分量的s 和t 进行局部连通度测试可以发现点割集S,所以单次采样可以判定出图G 不是一个k-VCC 的最小概率就是4(n-k-1)/n。 定理 3 采样T 次后都不能发现点割集S 的最小概率为ε=(1-Pr(E) )。 将ε 固定,近似算法框架为,在判定图G 是否为一个k-VCC 时,T 为近似算法计算局部连通度的次数,T'为精确算法计算局部连通度的次数,则min(T,T')可作为计算局部连通度的次数上界。当T 本节通过在不同真实数据集上进行实验评估概率采样算法的效率和有效性。本文提出的所有算法均采用C++语言实现,以用-O3 等级优化的GCC 9.20 编译。所有实验均在Windows 机器上运行,机器的配置为AMD Ryzen 3.20 GHz,16GB 内存。 本节用VCCE 表示第3 节中提出的精确算法,VCCE表示第4 节中提出的近似算法。 在实验中本节设近似算法的ε 为0.05,即最坏情况下会将一个不是k-VCC 的图误判为k-VCC 的概率为5%。 本小节研究VCCE 和VCCE在不同的真实网络上发现k-VCC 的运行效率。图1 给出了两种算法对于不同的k 的总体运行时间。从图1 中可以发现,VCCE在所有数据集中的运行效率都高于VCCE,并且运行时间差距很大。如果遇到近似算法退化时,即n,k 相差很小时所需计算局部连通度的次数可能会超过精确算法,近似算法框架便采用精确算法。由此可见,VCCE的运行时间不会超过VCCE。 图1: 不同真实数据集的运行效率 随着k 的增加,这些算法的运行时间呈下降趋势。这是因为,首先如果给定一个较大的k 值,由于受到k-core 的约束,有许多节点会在预处理阶段被过滤掉,所以图的规模会减小。其次是k 增大这表明更容易发现一组小于k 的点割集,这意味着图更有可能被分割为更小的子图。 本小节研究VCCE在不同真实网络上发现k-VCC 的有效性。对于同一个图G 和参数k,笔者以VCCE 计算出的所有k-VCCs 作为标准,然后与VCCE的计算结果进行对比。实验结果如表2,其中k~k为5.2 节中参数k 的设定。大量实验的结果表明VCCE发现的k-VCCs 正确率基本与理论相符,并且表现非常优异。这是因为,虽然最坏情况下会有5%的概率会将一个不是k-VCC 的图误判,但是当样本集巨大时,图的形态均匀分布,Pr(E)的概率会上升,所以在一般情况下误判的概率其实远低于5%,这也说明了VCCE能够应用于大规模图分析中。 表2: 不同真实数据集下的有效性分析 本文旨在损失少许精度的情况下高效发现大规模网络中的所有k-VCCs。首先归纳了现有的算法框架,指出了其瓶颈所在。其次在现有框架上提出了一种基于概率采样的近似算法,给出了误差分析与证明,结论得出在k 与n 相差较大的时候效率很高。最后笔者在三个真实网络数据集上进行了大量的实验,运行效率分析中近似算法均高于精确算法,而且在大规模网络中k 较小时即k 与n 相差较大,这恰巧是精确算法最薄弱的地方,精确算法花费的时间是巨大的。而近似算法却能很好的完成任务。有效性分析中,近似算法所发现的k-VCCs 几乎与精确算法的一致。实验说明了本文提出的近似算法在实际应用中具有巨大的实践价值。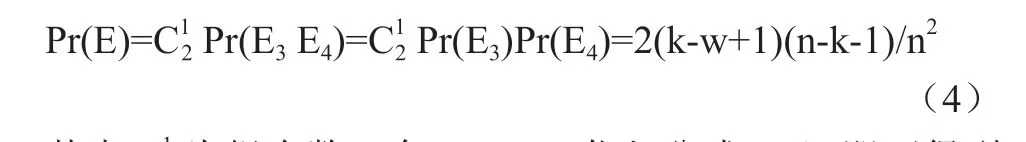



5 实验结果与分析
5.1 实验数据集和参数设定

5.2 算法运行效率分析

5.3 算法有效性分析

6 结束语

