基于机器学习预测流场特征的网格生成技术研究进展

韩天依星，皮思源，胡姝瑶，许晨豪，万凯迪，2，高振勋，2，蒋崇文，2，李椿萱

1.北京航空航天大学 国家计算流体力学实验室，北京 100191

2.北京航空航天大学宁波创新研究院 先进飞行器与空天动力创新研究中心，浙江 宁波 315832

美国国家航空航天局（NASA）总结了多年来AIAA 阻力预测研讨会（DPW）的研讨成果，认为网格是影响计算流体力学（CFD）计算精度的一大因素[1]。作为物理空间离散的主要手段，网格直接影响几何外形的逼近精度和流场的解析度，并与控制方程及边界条件的离散格式共同决定了数值误差水平及残差收敛特性[2]。随着物理流动和几何外形复杂度的提高，网格因素导致的数值误差将更加显著[1-3]。

高质量网格的生成需要充分考虑流动特征的解析性。由于出现边界层、激波层、分离/再附等流动结构的局部区域中流动参数梯度较大，需要在该类局部区域中采用更高的网格分辨率以保证计算精度[1-5]。因此，在传统CFD 的网格生成中，需要结合物理推理、理论模型、经验公式、试验数据等手段预估流动问题中需要解析的流动结构以确定初步的网格分布[2]。然而，DPW 会议的研讨认为，复杂流动结构往往难以进行先验预测[1]。对于未完全解析的流动结构，需要在计算中依据中间结果对需要加密的区域进行判断，结合自适应方法加密网格或进行网格重构以满足计算精度的需求[1-2]。

NASA在对CFD 2030年的展望中指出，未来的CFD应实现全过程的自动化，其中网格生成的自动化是实现CFD流程自动化的瓶颈问题，而流场特征解析的自动化则是高质量网格自动化生成的基础[2]。自适应方法通过对流场特征进行后验判断，可实现计算中的网格自动化加密[1-3]，而机器学习方法则为流场特征的先验预测提供了可能。

近年来，机器学习方法迅速发展，并在流体力学领域中得到了广泛应用[6-8]。基于流体力学实践中积累的大量数据，可以实现湍流模型封闭[9]、数据融合[10]、流场特征提取[11]以及流动预测[12]等目标。基于机器学习流场预测技术，结合流场特征提取方法，可建立流场特征预测模型，提供适用于网格生成的流场特征预估。在已知流场特征的基础上，通过网格自动生成技术即可获得高质量的计算网格[13-16]。

本文将以参考文献[13]和文献[14]的工作为基础提出一种基于机器学习预测流场特征的网格生成框架；并针对框架分别对可用于指导网格分布的流场特征指示器，实现流场预测所需的机器学习方法，以及部分网格自动生成及自适应方法等支撑技术进行了简要的综述；最后对该框架的实现进行了综合讨论。

1 基于流场特征机器学习的网格生成

通过梳理相关支撑技术，本文提出了如图1 所示的基于机器学习预测流场特征的网格生成框架。该框架主要包含6个部分：（1）将现有计算结果整理为数据库。若待研究流动问题对应的计算结果数据量不足，可在所考虑的工况及外形参数范围内补充一定样本点，通过传统CFD方法求解得到参考计算结果并加入数据库。（2）依据数据库中存储的计算结果，通过流场特征指示器提取流动结构特征以及流场中数值误差分布特征等流场特征数据。（3）将提取的流动及误差特征作为训练输出以训练机器学习模型，建立工况、几何外形与流场特征的映射关系。（4）机器模型训练完成后，输入新的工况及几何外形即可预测相应的流动及误差特征参考。（5）依据几何外形参考及流场特征参考，通过现有网格生成方法或网格自动生成技术即可得到适用于该流动问题的计算网格。（6）计算结束后新的结果将收录到数据库中，逐步完善机器学习模型，提高特征预测精度，用以持续改进网格生成质量。

图1 基于机器学习预测流场特征的网格生成框架Fig.1 Framework for grid generation based on flow features predicted by machine learning

基于上述思路，本文分别采用压力梯度判据提取高超声速钝头体头部激波[13]，采用摩擦力线的渐近线提取横向喷流的壁面分离再附线[14]，通过特征正交分解进行数据降维，训练全连接神经网络并预测流场特征。将此流场特征作为网格分布参考，通过参数化脚本程序实现结构网格自动生成。

2 流场特征指示器

流动特征的解析是网格生成的基础，是网格整体拓扑设计及网格密度选取的重要依据。例如，在超声速绕流问题中，计算域通常取为起始并贴近于头部激波上游的楔形或锥形体[17]；而为捕捉边界层流动，则往往需要依据雷诺数等参数估计边界层厚度及壁面y+值以确定壁面第一层网格高度[18]。另外，由于预估的流场特征存在较大误差或所研究的流动问题为非定常，计算推进过程中的流场特征可能偏离初始设计的网格分布，此时可通过网格自适应方法提高计算精度。

网格自适应方法中依据中间数值结果估计特征结构位置的过程由流场特征指示器完成。流场特征指示器通过对流场特征进行数学表示，结合特征判据将流场特征转换为特征线、面或区域，作为网格生成或数据处理的参考。此外，流场特征指示器还可与数值方法相结合，通过指示流场收敛状态构造动态计算域，进而提高CFD 计算效率[19-20]。当前常用的指示器主要包括两大类，其中流动结构指示器将流动结构特征作为网格分布参考，而流场误差指示器则直接估计数值计算误差作为网格加密依据。

2.1 流动结构指示器

流动结构指示器是针对流动结构的物理特性，通过分析结构及近邻区域内的物理量特征来识别相应结构的方法。现有的检测方法主要包括特征量、特征场及特征解三大类方法。

特征量方法主要关注流动结构的点特性。通常在激波、边界层等流动结构处流动参数存在较大的梯度，对可表征其流动结构的特征量设置阈值识别其特征是最直接和广被采用的方法[21]。例如，WENO类格式中模板的加权系数主要受梯度的影响。参考文献[23]～文献[25]建议梯度极值的判据为密度（或其他流动参数）的一阶梯度大于零，二阶梯度等于零。相对于固定阈值，若依据当地马赫数修改间断判据的阈值则可进一步降低数值耗散[22]。然而，梯度阈值的选取却难以先验确定。P.G.Buning 与J.L.Steger[26]提出以法向马赫数判据Man=1判断激波位置，结合压力梯度判断激波方向。考虑到压力梯度的扰动影响及其可能导致的对旁波波系的误判[27-28]，该方法同样需要设定阈值过滤，因此存在与梯度极大值判据相类似的问题。对于复杂外形的边界层识别问题，传统的99%无黏壁面剪切速度判据易受局部速度扰动的影响，且边界层外边界流动速度（无黏壁面剪切速度）也较难获取。而在低速流动条件下，流动总压不受局部扰动的影响，99%来流总压判据可准确捕捉壁面黏性作用影响区[29]。

特征场方法则是从流动结构的局部矢量场特性入手。R.C.Moura 等[30]通过有限时间Lyapunov 指数方法分析胀量（速度散度）的梯度场得到胀量场的脊线作为激波参考线。事实上，胀量自身也可作为激波间断判据的特征量[31-36]。M. Kanamori 和K. Suzuki[37-38]注意到特征线汇聚于激波处，因此通过求解特征线的线化方程即可确定激波的位置及方向，如图2 所示，无须设置阈值，且可推广至三维[39]及非定常[40]激波识别问题。

图2 网格单元提取渐近线[40]Fig.2 Extraction of asymptote in each cell[40]

特征解方法通常需要与其他方法相结合，以特征解匹配的方式取代特征量判据。黎曼解方法[41-42]通过考察局部数值解与一维黎曼解的匹配程度识别包括激波、接触间断、膨胀波系等流动结构；其黎曼解的特征方向可通过迭代方法得到，也可结合前述特征线方法[37-40]进行判断。流场特征量的梯度既可由有限差分计算得到，也可采用卷积计算确定。后一种方法对初步计算得到的流场数据或其图像表示进行卷积滤波，再通过特征解匹配的方式识别流动结构。H.Akhlaghi 等[43]通过Roberts 边缘检测方法处理稀薄流动数值纹影结果，给出其拟合Gauss分布曲线，如图3(a)所示，从而得到激波位置以及波前、波后参考位置。T. R.Fujimoto 等[44-45]则采用Sobel 边缘检测方法处理压力云图，并匹配Rangkine-Hugoniot关系式判定激波位置。

图3 激波处分子数密度及纹影函数分布[43]Fig.3 Number density and schlieren function distributions within the shock wave[43]

应该指出，以上方法存在互补之处。将三类方法进行有机结合还可进一步提高流动结构的辨识精度。

2.2 流场误差指示器

流场误差指示器着眼于数值计算误差，通过误差估计方法给出流场中的数值误差分布，根据设定的自适应判据确定网格加密区域。相较于流动结构指示器仅给出流动结构的位置，流场误差指示器更关注局部误差特征，适用于网格自适应方法。

Richardson外推法[46-47]主要基于数值解在精确解邻域的幂级数展开，依据在不同密度网格下的计算结果进行误差估计。该方法适用于有限差分、有限体积、有限元等离散方法，应用范围广泛[48]，但通常需要三套（若数值方法精度已知则为两套）网格的计算结果，计算量大，且在间断处其误差无法定义[49]。在Richardson外推法的基础上，τ估计法则只需已知不同密度网格下的计算残差，适用于多重网格方法[50-52]。

误差输运方程（error transport equation）方法[53-56]将计算结果与精确解分别代入原始方程或其离散方程，并取两者之差得到误差方程，通过求解该方程得到全流场误差。误差方程法可采用与原始方程相同的数值方法及网格，且能反映误差传播特性。相对于Richardson 方法，误差方程法可针对误差源区域网格进行加密处理以降低误差[57]。

伴随（adjoint）方法从误差积累的角度出发，针对部分数值计算中所关注的气动力、热等受局部误差影响的积分量得到全场误差对目标泛函（如升力系数等）影响的量化指标。首先，根据目标泛函给出与流动控制方程对应的伴随方程，随后求解该伴随方程即可得到全场误差的权重以决定网格加密尺度，进一步可对误差进行修正以提高目标泛函的精度。如图4 所示，局部误差方法仅对激波及尾迹等特征区域进行网格加密，而伴随方法在前者基础上对激波及尾迹上游区域进行了额外加密。当前基于伴随方法的网格自适应生成和误差分析的相关研究主要集中于有限元法和有限体积法（详见K. J. Fidkowski 和D. L. Darmofal[58]的综述）。但J.E.Hicken[59-60]的研究显示，伴随方法也可适用于分部求和类（summation-by-parts，SBP）有限差分法。此外，还出现了对非定常[61]、对偶一致性[62-63]等问题的相关研究。

误差指示器给出的误差分布需依赖自适应判据将其转换为网格分布。常见的自适应判据包括误差阈值、误差频数分布分位数、误差累积分布分位数等。自适应判据的误差阈值根据计算需求给定，当网格误差超出阈值时即进行加密，密网格的尺度由粗网格尺度、误差及误差阶数综合考虑确定[64]。基于误差频数分布分位数的判据直接限定需要加密的网格数量，可较好地控制网格总数[65]。而误差累积分布分位数则是控制粗网格对误差的总贡献值[66]。但该判据在实际应用时可能由于少量网格出现局部较大误差，导致自适应加密流程过慢。

3 流场预测的机器学习方法

前述流场特征指示器均采用后验的方式在流场数据的基础上提取流场特征，而机器学习方法则为流场特征的先验预测提供了可能。通过预先训练的机器学习模型，有望在CFD流程开始时便可给出新工况条件下的流场数据；或在训练阶段即与流场特征指示器方法相结合，直接预测拟识别的流场特征，依据该特征设计网格拓扑及密度分布，改善网格生成质量。

3.1 基本机器学习方法

流动问题的数值模拟结果形式上是在离散网格单元上反映其物理空间中流场特征的高维数据表示。通过提取流场特征数据进行数据降维，对数据的低维表示进行分析预测是应用机器学习优化网格生成的基本思想之一。特征正交分解（POD）方法是流体力学领域中广泛使用的一种线性数据降维方法，与机器学习领域中的线性主成分分析（PCA）相对应，可表示为采用线性激活函数的浅层自编码器。而在传统POD 方法基础上添加滤波器可得到介于POD 及离散傅里叶变换（DFT）间的谱特征正交分解（SPOD）方法[67]。

自编码器（AE）是机器学习领域中用于数据降维表示的一类神经网络框架。自编码器通常由编码器及解码器两部分构成，其中编码器将原始数据映射到数据的降维表示，而解码器则将降维数据重构为原始数据的近似表示。相对于POD/PCA方法对应的浅层自编码器，采用非线性激活函数并增加自编码器的神经网络层数，有望获取数据的复杂非线性特征，从而得到更为紧致的降维表示[6]。自编码器中的编码器及解码器可由全连接神经网络构成，也可由下述卷积神经网络或其他网络构成。

卷积神经网络（CNN）是一类由卷积运算及其辅助运算构成的神经网络结构，适用于处理具有一定空间结构的数据，在特征提取相关问题上具有优势。CNN源于神经科学的试验发现：视觉系统前端神经元对特定光模式如定向条纹等性质敏感，对视网膜图像的局部特征具有选择性[68-70]。受试验启发，CNN通过构造卷积单元模拟视神经工作方式以实现数据空间特征的识别。在每个卷积单元中，通过对原始数据进行卷积运算，可得到其梯度等局部特征的信息。随后对局部特征信息进行综合处理，能够实现空间结构信息的高效利用。此外，相对于全连接层每个输入与每个输出均产生交互，卷积层的输出单元仅与局部的输入单元产生交互。该稀疏交互特性令CNN在网络的存储及计算效率上具有优势。

3.2 基于机器学习的特征提取

W.R.Wolf 等[71]采用SPOD 方法结合全连接神经网络对大涡模拟（LES）结果进行了降维处理，构造了二维圆柱及翼型的非定常绕流的降阶模型。N.Omata 和S.Shirayama[11]结合CNN与自编码器，构建了二维翼型绕流的降维表示。而T.Murata等[72]则在CNN自编码器的基础上，通过多个不同的解码器实现模态分解，最终将不同的重构模态线性叠加得到重构流场。对于二维圆柱绕流，在模态分解中使用线性激活函数表示时，模态分解CNN 自编码器（MD-CNN-AE）的表现与POD类似，而使用非线性激活函数时其重构精度高于POD。图5呈现了三者给出的重构模态对比。相较于传统的CNN自编码器，MD-CNN-AE可以直观地获得不同模态的流场结构。

图5 POD、线性MD-CNN及非线性MD-CNN流向速度重构模态及横向速度重构模态云图对比[72]Fig.5 The decomposed flow fields with POD,MD-CNNLinear and MD-CNN-tanh[72]

N.Thuerey等[73]基于U-net网络结构对不同来流雷诺数及迎角条件下的不同翼型绕流流场进行了预测。在传统的CNN自编码器的基础上，U-net在解码过程中并入了编码过程中同级卷积层的输出，解码过程能够综合考虑编码中的低维信息。

3.3 基于机器学习的流场预测

S.Bhatnagar 等[74]采用类似CNN 自编码器的网络结构，其输出层为翼型绕流场，输入层为网格点到翼型壁面间距所构成的标量场（壁面距离场），且在隐藏层附加了工况参数迎角和雷诺数的输入，实现了对不同翼型在不同工况条件下绕流场的预测。不同于通常的CNN方法需要在规则的笛卡儿背景网格上插值，A.Kashefi等[75]采用了PointNet[76]网络结构直接对计算网格点进行处理，能够预测不同物体的绕流场。

M. Raissi 等[77-84]提出了物理嵌入的神经网络框架（physics informed neural network，PINN），通过在损失函数中引入控制方程，仅根据初边值条件即可预测流场的时空分布，实现对偏微分方程的求解，如图6 所示。S.Lee 和D.You[85]的计算结果表明，采用物理嵌入的CNN 对非定常圆柱绕流的预测结果优于未采用物理嵌入的CNN预测结果。将控制方程、相似参数、理论模型等流体力学研究成果以物理嵌入方式纳入机器学习框架，能够显著降低机器学习预测流场的数据要求。

图6 PINN方法求解一维Burgers方程[77]Fig.6 Solve a 1D Burgers equation with PINN[77]

4 网格自动生成及自适应技术

网格技术仍是当前CFD计算效率的瓶颈问题[2]。在本文所提框架中，依据预估特征生成相应网格的关键步骤需要网格自动化生成技术的支持。

4.1 结构网格拓扑生成技术

相对于采用非结构网格的CFD程序，采用结构网格的CFD程序通常在计算精度、收敛性、数据存取、程序编制上均具有一定的优势。但对于具有复杂几何外形及流动特征的流动问题，网格的生成需要耗费大量机时，网格质量往往难以保证。近年来，结构网格的自动化生成技术发展迅速，基于网格拓扑的构建模式形成了标架场法、铺层法、中轴法等几类方法。综合使用多种方法能够有效地对复杂几何进行二维结构网格生成，但三维条件下拓扑分划与网格密度分布的综合控制仍有待进一步研究。

4.1.1 标架场法

标架场方法是近几年首先在计算机图形学领域中提出，可用于拓扑结构分析，并逐步推广应用于复杂几何结构网格生成的方法。该方法基于结构网格单元与标架结构的对应关系，将标架场转换为易于求解的数学表示，通过设计控制方程及相应边界条件进行求解，即可从其数值解实现几何区域的拓扑分解并生成网格。此外，标架场也可通过铺层法及中轴法确定。

二维标架场可以通过如图7 所示的模式转换为矢量场[86]。对于三维标架场，出现了不同的标识模式：Jin Huang等[87]引入球面调和函数，以旋转矩阵表示标架场[88-90]；A.Chemin 等[91]提出了四阶对称张量表示法；而D.Palmer 等[92]采用微分与代数几何方法描述标架结构以更好地捕捉计算域中的奇异结构。N.Kowalski 等[93]将热扩散方程作为矢量控制方程，在给定边界矢量条件下求解首先得到如图8所示的矢量场（见图8(a)）及相应的标架场（见图8(b)），再通过分析场中的奇异结构得到拓扑分划（见图8(c)），并在给定网格分布后完成结构网格（见图8(d)）的生成。标架场方法所得拓扑结构中通常具有较少的拓扑奇点数量（见图9），对复杂外形能够生成高质量的结构网格（见图10）。

图7 n对称标架转换为矢量[86]Fig.7 n-symmetry direction transform to a vector[86]

图8 标架场方法生成二维结构网格[93]Fig.8 Generation of a 2D structured grid using cross field method[93]

图9 中轴法及标架场方法对凹腔结构处理[94]Fig.9 Comparison between dealing with concavities using medial axis methods and cross field methods[94]

图10 标架场方法生成三维结构网格[95]Fig.10 Generation of a 3D structured grid using cross field methods[95]

4.1.2 铺层法

铺层法[96-98]是通过边界推进生成结构网格的方法，在考虑二维计算域时也称为铺路法[99-100]，如图11 所示。该算法从边界向内部推进，当推进面交叉时，通过缝合、拆分与回路连接等手段进行网格平滑过渡，最终生成可覆盖整个区域的结构网格。铺层法生成的网格可高质量地匹配较复杂的几何外形。然而，由于铺层法主要考虑局部的几何拓扑结构，往往需要附加约束以避免出现过多的奇点。同时，在三维条件下形成的中心间隙拓扑复杂，六面体填充方法尚不完善。因此，单独采用本方法生成网格难以完全克服以上缺陷。

图11 铺层法示意图[98]Fig.11 Scheme of paving method[98]

H.J.Fogg等[101]将铺路法与标架场法相结合能够实现二维标架场的快速生成。如图12 所示，该方法从边界向内逐层推进标架结构并铺满整个计算域，在平滑操作后即可得到适用于结构网格生成的标架场。其中，在进行平滑操作时可通过预设度量张量场实现网格密度分布控制（见图13）。

图12 铺层法生成二维标架场[101]Fig.12 Generating cross field by paving method[101]

图13 度量张量场控制网格密度分布[101]Fig.13 Grid refinement control by metric tensor[101]

4.1.3 中轴法

中轴法[102-103]通过局部区域内相切圆/球心的轨迹线将该区域划分为可结构网格化的凸子区域并分别生成网格，如图14 所示。该方法生成的网格具有较好拓扑结构。在各子域中网格拓扑奇点至多只有一个且远离几何边界。但对于具有复杂外形的计算域，该方法鲁棒性较差，难以对凹腔结构进行较优的拓扑分划。而H.J.Fogg等[103]借助标架场改善了中轴法对凹腔结构的处理能力。该方法在中轴线上逐步推进，依据中轴线两侧的几何边界夹角配置标架场（见图15）。在标架场配置完成后检测并重构奇点构型，对网格进行拓扑分划，结果如图16所示。

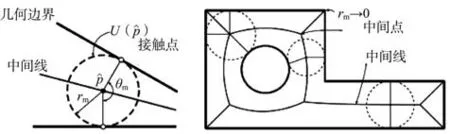
图14 中轴法示意图[103]Fig.14 Scheme of the medial axis method[103]

图15 几何边界间标架场配置[103]Fig.15 Cross field between geometric boundaries[103]

图16 中轴法生成二维结构网格[103]Fig.16 Generation of a 2D structured grid using medial axis methods[103]

4.2 网格自适应技术

实际计算中由于流动特征预测误差或流动非定常特性，所需网格加密区域与初始网格加密区域存在偏差。网格自适应技术是一项相对成熟的网格技术[104-108]，能够以较小的网格量为代价集中加密所需区域，是解决上述问题的一种可行方法。依据自适应的实现方式，现有自适应方法主要可归纳为p 型、r 型、h 型三类。p 型方法令网格保持不变，通过修改数值格式提高流场的分辨率。r型方法则保持拓扑结构不变，通过移动网格节点坐标改变网格分布，在网格自适应周期中可保证较高求解精度，但网格点移动可能导致网格局部失真，引起数值振荡。而h 型方法采用剖分及聚合网格单元的方式改变网格分布，适用于局部精细特征的捕捉，是目前实际工程中采用最为广泛的网格自适应方式。对于尾迹、旋涡等需要在大范围区域加密的流动特征，可如图17所示采用h型方法加密[109]。而激波结构则往往要求各向异性加密，通过重构网格面方向可显著降低加密网格量需求。Zou Dongyang 等[110]将激波装配法嵌入非结构网格自适应过程中（见图18），通过网格重构方式匹配激波位置，间断前后变量关系由理论解给出，无须进一步加密，仅采用r 型方法即可实现激波的精确模拟。而A.Corrigan 等[111]和A.D.Kercher 等[112]采用移动DG 方法实现了与上述激波装配嵌入方法类似的非结构网格自适应重构。L.M.D'Aquila 等[113]则通过改进重构方法提高了激波装配嵌入方法的稳定性。

图17 非结构网格动态加密捕捉翼尖涡[109]Fig.17 Dynamic adaption of the unstructured grids near the tip vortexes[109]

图18 激波装配嵌入的非结构网格重构[110]Fig.18 Shock-fitting embedded reconstruction of unstructured grids[110]

对于网格自适应的密度控制，现有研究发展了多种基于度量参考的网格自适应方法[108]。A. Loseille 等[114-116]提出了基于Hessian矩阵的多尺度度量，可保证网格自适应过程达到全局二阶收敛，适用范围广[106]。A.Loseille 等[117]将多尺度度量推广到目标泛函的误差控制，提出了基于伴随的度量，并进一步扩展到高阶数值方法[118]。V. olejsi等[119-120]针对hp 型自适应方法基于高阶Taylor 多项式插值提出了Lq范数度量，适用于高阶数值方法，并推广到了任意流动误差指示器[121]。K.J.Fidkowski 等[122-123]研究表明“熵状态变量”与熵平衡方程的伴随解相似。相较于传统伴随方法需要额外求解伴随方程，熵状态变量作为伴随解仅需通过气体状态变量直接计算得到，计算需求小。

5 机器学习预测流场网格生成的实现

本文提出的基于机器学习预测流场特征的网格生成框架核心是利用机器学习的预测能力对一般流场特征进行先验预测，建立工况及几何外形与流场特征的联系。在实践中，此类联系若要依赖理论模型或经验公式提供，则难以达到相对较宽的通用性。本文第2～4节分别介绍了在第1节所提框架下机器学习网格生成所需三项支撑技术的研究近况。而本节将介绍机器学习网格生成实现方法的相关研究。

上述三项支撑技术中部分方法已分别用于机器学习相关的网格生成中。现有研究主要通过机器学习方法替代或辅助现有技术中的复杂算法以提高效率。在流场间断识别问题中，可将已知间断状态的数值分布作为训练集，通过机器学习方法构建模板点数值分布与间断状态的联系。D.Ray与J.S.Hesthaven[124-125]、Wen等[126]和A.D.Beck等[127]均采用了光滑/非光滑函数库作为训练集。而Feng Yiwei等[128]则采用单层神经网络基于一维黎曼问题数值解训练间断指示器，并应用于间断伽辽金(DG)方法中[129-130]。在非结构网格自动生成问题上，通过机器学习方法可构建关于几何特征[131-132]、误差特征[133]到网格分布的映射关系，在保证网格质量的条件下可提高网格的生成效率。

对于三项支撑技术的综合应用，基于机器学习预测网格分布密度的非结构网格自动生成方法研究采取的思路与本文框架类似。Zhang等[13]依据两套网格的泊松方程计算结果进行了误差估计，通过三种不同的神经网络建立了几何及边界条件与误差分布的映射关系。K.Huang等[14]针对随机外形的低速绕流问题设计了带约束随机外形的生成方法，利用伴随方法进行误差估计，在U-net网络基础上实现了误差预测以指导非结构网格的生成。

本文基于本文框架分别对高超声速钝头体绕流问题[15]和平板横向喷流干扰问题[16]进行了结构网格自动化生成的尝试。对于流场特征指示器，考虑到高超声速钝头体问题中激波结构较为单一，梯度阈值影响相对较小，激波识别采用了压力梯度判据。而考虑到喷流干扰的分离再附线与压力峰值线存在相关性，将摩擦力线渐近线提取方法结合壁面压力分布进行判断可提高特征提取的鲁棒性。

本文采用的流场预测方法均由POD 降维及全连接神经网络建立映射关系两部分构成。传统POD 方法通常要求每条数据长度相同，以背景网格作为采样网格。而本团队采用的采样网格则根据喷口直径及分离线尺度自动生成，如图19所示。将背景网格作为采样网格具有较高的通用性。而依据几何外形特征及流场特征生成采样网格可提高不同条件下流场的相似度，有利于减轻数据降维及后续神经网络训练的数据需求量负担，但流场特征尺度需要通过机器学习方法或其他方式另行给出。最终生成的计算网格结构如图20 所示，分离线处存在网格约束曲线，再附线处未作特殊处理。

图19 采样网格结构及壁面压力系数分布[16]Fig.19 Scheme of sampling grid and contour of wall pressure coefficient[16]

图20 计算网格结构及壁面压力系数分布[16]Fig.20 Scheme of computational grid and contour of wall pressure coefficient[16]

若进一步将不同的流动特征逐步嵌入采样网格中，则有望实现如图21所示的数据降维框架。该框架包括5个部分：（1）在得到流动特征后进行特征分层处理，得到从总体到细节不同层次的流动特征。分层特征可存储在背景网格G0中。对于简单特征也可采用代数表示。（2）依据几何特征及总体流动特征建立采样网格Gi+1，将计算网格上的流动特征插值到采样网格进行数据采样。（3）采样特征同时作为编码器的训练输入以及解码器的训练输出用以训练自编码器。训练完成后编码器和解码器可以单独使用。（4）将工况及几何外形作为神经网络预测模型的训练输入，将编码器输出的降维特征以及步骤（1）中得到的总体流动特征作为训练输出，用以训练神经网络预测模型。（5）训练完成后，输入工况及几何外形预测模型即可输出降维特征及分层特征。其中分层特征结合几何外形可重构采样网格；降维特征通过解码器可重构为采样特征指标集。采样网格和指标集共同构成采样特征，与流动特征对比验证预测精度。当模型预测精度未满足要求时，返回步骤（1）进行迭代，在更优的采样网格上进行特征分层，并在后续步骤中采用更多的特征参考生成采样网格进行数据采样。

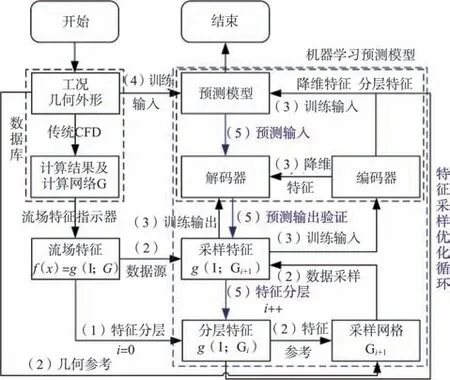
图21 特征分层采样的数据降维框架Fig.21 Framework of dimension reduction based on progressive feature extraction

应该指出，上述数据降维框架本质上利用所研究流动问题中已知的共性特征等附加信息，将相似参数及流动拓扑结构嵌入神经网络中以减少神经网络需要学习捕获的特征，从而减少训练集的样本容量需求。可以想象，在实践中以上措施将更依赖于专家知识，在通用性上受到流动问题自身特性的限制。在本团队尝试的两类问题中，几何外形均较为简单，可表示为少量外形参数。但对于复杂曲面外形则有必要通过自编码器等方法进行数据降维[74]。若已知几何外形的设计方法，则可将复杂外形表示为少量设计参数，简化几何外形表示。特别是在乘波体设计[134-135]中，几何外形与主要激波结构往往由设计型线及少量设计参数同时决定，在设计工况条件下可直接作为计算网格和采样网格生成的参考。

本文采用的网格生成方法系通过参数化脚本程序实现，需要预先人工生成相应流动问题的模板网格。在特征分层采样的数据降维框架中，需针对特定流动问题的分层特征设计具备总体到细节不同层次特征的模板网格。该系列模板网格既作为采样网格使用也参与计算网格生成。考虑到现有结构网格自动生成方法仍有待于进一步完善，而特定工程应用中的几何外形及流动特征具有较高的一致性，基于模板的结构网格参数化生成方法不失为工程应用的一种选择。

6 结束语

本文针对基于机器学习预测流场特征的网格生成框架，对流场特征指示器、基于机器学习的流场预测、网格自动生成及自适应三项支撑技术进行了简要综述，并对该网格生成方法的实现进行了综合讨论。

现有流动结构指示器研究主要针对数值求解与数据提取，尚未与网格生成广泛结合。自适应网格方法的主要判据仍为简单特征量阈值判据。伴随-自适应方法相对成熟，但在工程实践上仍需进一步完善。现有机器学习框架能够较好地完成简单流场预测，但对于工程实践中的复杂流动仍有待针对性研究。结构网格的自动生成方法仍在积极发展中，但在针对流体力学问题的网格控制有待进一步完善。

本文提出的基于机器学习预测流场特征的网格生成框架，在上述相关技术的进一步完善下，有望通过充分应用已有的流场数据积累，开发出兼顾几何外形及流动特征的高质量网格生成软件模块，以降低网格生成的耗时，减轻计算中网格自适应需求，从而提高CFD工程效率。