“数值分析”课程教学中的“分而治之”思想

马俊杰

贵州大学数学与统计学院 贵州贵阳 550025

一、“数值分析”课程改革的意义与现状

全国高校思想政治工作会议上强调“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面”“各门课程都要守好一段渠、种好责任田，使各类课程与思想政治理论课同向同行，形成协调效应”。基于全面育人的课程改革是高等教育面临的重要问题，也是高等教育发展的必然[1]。“数值分析”作为数学以及理工科专业的重要课程，主要面向高年级本科生以及低年级研究生开设。课程内容一般包含微积分、非线性方程、线性方程组、特征值和特征向量、微分方程初值问题、微分方程边值问题等，需要高等数学、线性代数、常微分方程等前序课程[2]。因此，“数值分析”的教学内容覆盖面较大，难度也较高。同时，由于它包含了多门数学类课程，在“数值分析”教学中融入思政教育具有更丰富的内涵，也更有利于学生的全面发展。

“数值分析”课程教学侧重数学问题的数值计算方法，是连接计算机与模型问题的重要纽带，可以培养学生结合抽象思维与实际行动的能力。自上世纪80年代全国高校普遍开设这门课程以来，“数值分析”的课程改革已经取得了许多成绩。例如，大量实验课程的设计以及引入丰富了教学内容，并使得教学过程更加具象，加深了学生对知识点的理解[3]；通过针对专业区分选取教学体系，兼顾了具有不同数学基础的学生的学习进度[4]；通过引入学科前沿，使得人才培养更加适应社会的发展需求[5]。但是仍需注意的是，“数值分析”教学内容过于烦琐，在大多数学校这门课程的课时量比较有限，教学过程欠缺“可视化”、课程考核不合理等问题仍是课程教学面临的重要问题。因此，如何在教学任务紧张、教学内容复杂的情况下融入思想教育实现全面育人是一个重要的课题。

事实上，全面育人与传统教学内容不是相互排斥的两个个体，而是相互促进，相辅相成的。以“数值分析”为例，由于课程教学过程中不可避免大量烦琐的公式推导，学生很容易产生厌学情绪[6]。如果可以合理引入思想教育提高学生的学习积极性，不但有利于课堂教学的开展，而且可以提升教与学的效率。当前“数值分析”课程改革主要关注如何在专业知识的学习过程中融入思政元素，强调学与思的巧妙结合。例如，通过短片向学生介绍使用课程内容解决实际问题的案例，宣传科技工作者在第一线的感人事迹，增强学生的自豪感；通过结合数学史与数学文化，将我国古代数学的重大成就讲授给学生，例如秦九韶算法，进而培养学生的文化自信[7]。但是，“数值分析”课程不仅具有内容丰富的特点，而且包含许多算法构造思想。本文以“分而治之”为落脚点，分析这种思想与辩证唯物主义的关系，培养学生树立正确的辩证唯物主义和掌握科学的方法论，并总结教学过程中“分而治之”的应用。

二、“分而治之”思想与课程改革思路

“分而治之”思想是算法设计的一种技术，即先将复杂问题分解成数个小问题，针对每个小问题设计算法，进而组装成原复杂问题的解。这种思想是辩证唯物主义中“具体问题具体分析”这一方法论在算法设计领域的体现。在“数值分析”教学中注重总结算法设计的“分而治之”思想，建立它与辩证唯物主义、建设中国特色社会主义伟大成就的联系，不仅可以增强学生的爱国热情，而且可以提高学生对算法设计的认识。在“数值分析”教学中融合算法设计思想需要做到以下几点。

第一，组建“数值分析”教学团队，增强教师全面育人意识，提高教师全面育人水平。对于专业课教师，全面育人仍是一个较为陌生的课题。主要原因在于专业课教师在成长过程中将大部分精力都投入科学研究、教材教法等方面，缺乏全面育人教法的培训。组建教学团队的优势是可以通过集体学习的方式使得教师在最短时间成长为全面育人方面的专家。

第二，正确处理课程教学与全面育人的关系。课程教学是教师的主要任务，只有完成大纲要求的教学内容，才能真正实现人才培养的目标。人才的成长应该是全方位的，而不是机械化的，仅仅学习教材中固定知识点的人才不符合当今社会的发展。只有通过全面育人加强学生思维、思想的教育，才能帮助学生成长为社会需要的人才。另外，设计合理的全面育人内容有助于提高学生的学习积极性，提升课程教学效率，进而有效地解决“数值分析”课程内容多、课时少的问题。

第三，创建全面育人平台，结合线上线下教学夯实全面育人基础。数学类课程具有教学内容抽象、知识结构严谨的特点，对于普通高校的学生，通过自学掌握大纲知识点的难度很大。因此，数学类课程教学改革的重点集中在提高知识传递效率、准确性以及借助现代可视化工具将抽象概念具象化。但是，应该注意的是学生通过课下自学的方式达到培养目标仍是十分困难的，而全面育人内容更加贴近生活生产实践，更加具体，从而更有利于发挥课外学习的优势。通过建立系统性的线上全面育人材料，结合线下教学内容，可以充分发挥学生的主观能动性，提高教与学的效率。

第四，发挥先进计算平台优势，增强教学内容可视化。建设基于多媒体技术的智慧教室，将Matlab数值实验案例引入课堂教学，发挥与传统教学互补的优势，不仅可以激发学生学习兴趣，还可以提升教学效果。例如，在讲解最佳多项式逼近问题时，可以借助Matlab中的Chebfun工具箱，实现伯恩斯坦多项式的快速计算。通过讲解伯恩斯坦多项式的生成代码，结合最佳逼近数值结果，可以激发学生的学习兴趣，进而为全面育人提供讲授空间。

第五，强化数值案例设计，提升学生主观能动性。“数值分析”作为连接数学模型与实际问题的纽带，可以提高学生解决实际问题的能力。因此在实验案例的选取过程中，应该更多地倾向于与实际问题相关的模型，例如德拜温度模型、棒球运动轨道模型、光学散射积分问题、化学热反应模型、传染病模型等。模型的合理选择可以使学生产生对“数值分析”教学内容的兴趣。通过对实验教学环节的重视，可以加深学生对课堂教学内容的理解，为“数值分析”全面育人提供了肥沃的土壤。

三、“分而治之”思想教学总结

拉格朗日插值既是数值逼近的重要内容，也是数值积分、数值微分、微分方程数值等的基础[8]。一般地，对于插值节点x0…xn以及函数值y0…yn，可以找到不超过n次的多项式pn(x)使得pn(xi)=yi,j=0…n。在实际应用中，插值节点一般选取为等距节点。对于函数f(x)=sin(x)，分别取n=5和n=50，可以计算如图1中的插值多项式。从图中看出当插值节点增加时，拉格朗日插值函数对原函数的逼近效果是变好的。

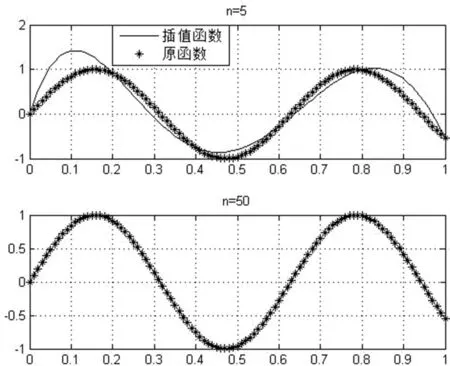
图1 拉格朗日插值法的逼近效果，原函数为f(x)=sin(x)

但是，当原函数变为Runge函数时，重复同样的实验结果大不相同(见图2)。通过实验结果的对比，可以使得学生更加具体地理解拉格朗日插值法的局限性。

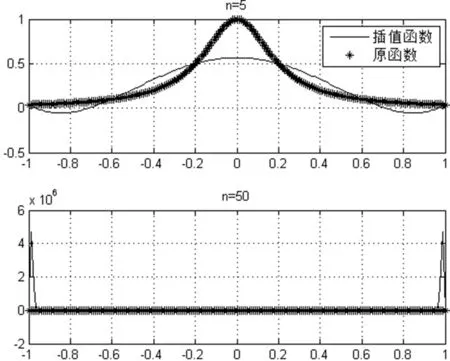
图2 拉格朗日插值法的逼近效果，原函数为龙格函数

任何算法的设计都是在已有方法的基础上针对实际计算中遇到的问题不断完善而得到的。在遇到拉格朗日插值法无法逼近龙格函数这一问题时，可以适时地引入“分而治之”思想，并结合唯物辩证法中的“具体问题具体分析”对学生进行讲解。具体到本案例，“分而治之”即将原区间上的插值问题分割成小区间上的插值问题。在小区间上，可以仅仅使用低次插值，例如线性插值，然后将所有低次插值函数连接成大区间上的插值函数，即得到图3。可以看出，将拉格朗日插值结合“分而治之”思想可以很恰当地解决龙格函数的插值问题。

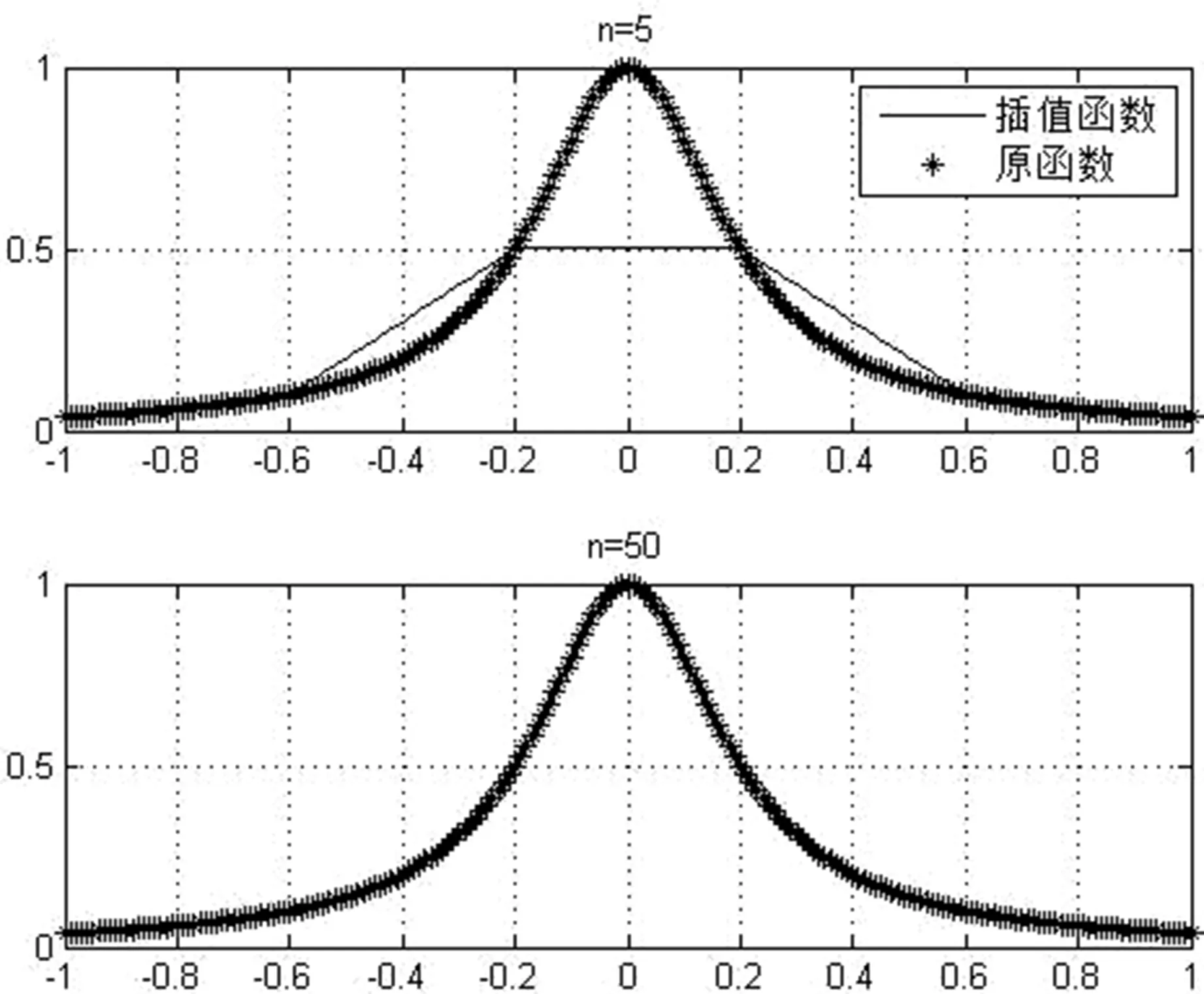
图3 拉格朗日插值法结合“分而治之”思想的逼近效果，原函数为龙格函数

在定积分的数值计算中，也常使用“分而治之”思想。牛顿—科特斯公式是计算数值积分的常用工具[9]。考虑使用梯形公式计算定积分:

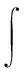
利用Matlab可得它的近似值为0.099916708323414，它的真实值是0.099944461108277，绝对误差仅仅为0.000028。所以梯形公式的计算结果是十分精确的。当积分区间延长为[0，1]时，使用梯形公式可得近似值为0.092073549240395，它的真实值是0.946083070367183，绝对误差为0.85401。所以梯形公式的计算结果是不可靠的。在此可引入“分而治之”思想，先将区间[0，1]划分为10个小区间[0，0.1]，[0.1，0.2]，[0.2，0.3]，[0.3，0.4]，[0.4，0.5]，[0.5，0.6]，[0.6，0.7]，[0.7，0.8]，[0.8，0.9]，[0.9，1]。对每个小区间使用梯形公式，然后利用积分的可加性将计算结果组合在一起即可得到。相应计算结果为0.945832071866905，绝对误差为0.00025。计算精度比直接使用梯形公式提高了很多，也体现了“分而治之”思想的优越性。

“分而治之”思想在矩阵特征值计算、稀疏线性系统的快速求解、常微分方程初值问题数值解等方面也有重要应用，在遇到复杂系统或者多尺度问题时，根据问题的不同部分的不同性质设计针对性的算法，是解决实际问题的重要技术。

结语

“分而治之”思想是数值算法设计的重要技术，由这一思想引出大量经典数值方法，例如分段低次多项式插值、三次样条函数插值、复化牛顿—科特斯公式等[10-12]。在“数值分析”的教学实践中，注重总结算法设计思想并将其融入课堂教学，不仅可以提高教学效率，而且有助于实现全面育人的目标。