含参集值优化问题近似解集的稳定性

孟旭东

(南昌航空大学 科技学院，江西 共青城 332020)

集值优化问题是标量优化问题和向量优化问题的拓展，是现代运筹控制优化领域研究热点之一.核心原因主要涉及3 方面：其一，就理论层面而言，集值优化问题的研究为诸多理论研究发展提供了统一模型，例如：Ky Fan 不等式、目标优化问题、向量均衡问题、向量变分不等式、偏微分方程反问题等；其二，从实际应用角度分析，集值优化问题在图像处理问题、生命生存理论、数理经济学与微分包含、交通网略等方面均有广泛应用；其三，集值优化问题的研究与非线性理论、非光滑分析、凸优化、变分学等现代数学理论紧密相关，且其自身理论及算法研究也需要新的概念、方法和工具.因此，对集值优化问题的研究有着极其重要的理论意义和应用价值，近年来备受广大研究工作者的青睐，且有了较丰硕的研究成果[1-10].众所周知，集值优化问题（近似）解集的稳定性分析是集值优化理论与算法设计中的一个重要课题.一般而言，集值优化问题及相关问题的稳定性研究是指分析（近似）解集受到参数变化时的扰动性质，主要包含定性性质和定量规律.定性刻画方面主要涉及Berge-半连续性、Hausdorff-半连续性、紧闭性、连通性、适定性等，定量性质主要包括Aubin 性质、平静性、Hölder 连续性、Lipschitz 连续性等.一些作者已经研究了（参数）向量均衡问题的映射解的半连续性，特别是下半连续性[11-18].但很少有学者研究参数集值优化问题（近似）解映射的上半连续和下半连续.Xu 等[19]得到了具集优化准则的参数集值向量优化问题极小解和弱极小解集映射上、下半连续性和闭性.孟旭东[20]获得了2 类含参广义集值平衡问题近似解映射的上半连续性和下半连续性定理.孟旭东[21]分析了基于改进集的参数集值优化问题解集映射的Berge 连续性、Hausdorff 连续性、C-Hausdorff 连续性和紧闭性定理.利用集值分析与变分分析方法，彭兴媛等在文献[22-26]中分别建立了带等式与不等式约束的向量平衡问题孤立有效解和弱严格有效解的最优性条件.本文在赋范线性空间中借助广义凸性和水平映射的方法，研究了目标函数和约束函数具参数扰动时参数集值优化问题2 种（弱）近似解集的上半连续性和下半连续性的最优条件.

1 预备知识

本文设X,Y,Z为赋范线性空间，Λ,Ω ⊂Z为非空子集，K⊂Y为闭凸点锥且intK≠Ø，M,N⊂Y为非空子集，记R+={x∈R|x≥0}.设点e∈intK，对任何的ε ∈R+，M与N的 ε-下序关系与弱 ε-下序关系分别定义为：

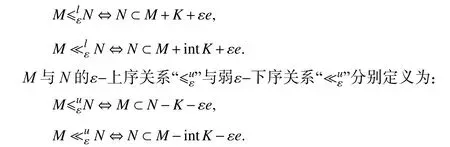
设F:X×Λ×Ω ⊂X×Z×Z →2Y{Ø}，T:Ω ⊂Z →2X{Ø}为给定非空集值映射，对每个点(λ,μ)∈Λ×Ω，讨论如下含参集值优化问题（简称问题（PSOP））：

问题（PSOP）：minF(x,λ,μ)，使得x∈T(μ).

定义1[26]设M⊂Y为非空子集，点ω∈M给定.

（ⅰ）假如(M-ω)∩(-K)={0}成立，则称点 ω为关于K的最小点，记为ω ∈Min(M).

（ⅱ）假如(M-ω)∩(-intK)=Ø成立，则称点 ω为关于K的弱最小点，记为ω ∈WMin(M).

（ⅲ）假如(M-ω)∩K={0}成立，则称点 ω为关于K的最大点，记为ω ∈Max(M).

（ⅳ）假如(M-ω)∩intK=Ø成立，则称点 ω为关于K的弱最大点，记为ω ∈WMax(M).

据文献[26]知：

注1（ⅰ）若M⊂Y为非空紧子集，则Min(M)≠Ø且Max(M)≠Ø.

（ⅱ）若M⊂Y为非空紧子集，并注意到Min(M)⊂WMin(M)及Max(M)⊂WMax(M)，则WMin(M)≠Ø且WMax(M)≠Ø.

定义2设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为给定非空集值映射，设点e∈intK，对每个点(ε,λ,μ)∈R+×Λ×Ω，以及点x0∈T(μ)：

（ⅰ）假如对任何的点x∈T(μ)，满足有

则称点x0为问题（PSOP）的l-最小近似解，记问题（PSOP）的l-最小近似解集为Sl(ε,λ,μ)，即

（ⅱ）假如对任何的点x∈T(μ)，满足有

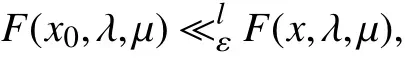
则称点x0为问题（PSOP）的弱l-最小近似解，记问题（PSOP）的弱l-最小近似解集为(ε,λ,μ)，即

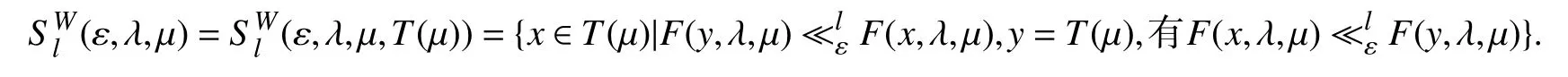
（ⅲ）假如对任何的点x∈T(μ)，满足有

则称点x0为问题（PSOP）的u-最小近似解，记问题（PSOP）的u-最小近似解集为Su(ε,λ,μ)，即

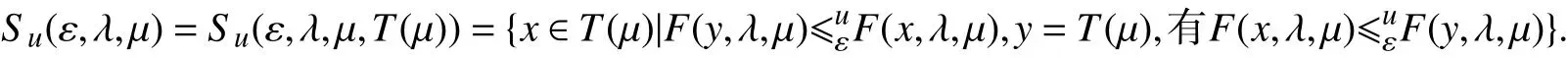
（ⅳ）假如对任何的点x∈T(μ)，满足有

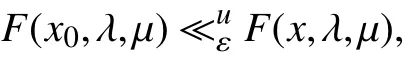
则称点x0为问题（PSOP）的弱u-最小近似解，记问题（PSOP）的弱u-最小近似解集为(ε,λ,μ)，即

注2据定义2 易得：

（ⅰ） 假如点x0∈Sl(ε,λ,μ)，y0∈T(μ)，且则必有点

（ⅱ） 假如点x0∈Su(ε,λ,μ)，y0∈T(μ)，且则必有点

注3设点e∈intK给定，对每个点(ε,λ,μ)∈R+×Λ×Ω，则：

（ⅰ）Sl(ε,λ,μ)⊂(ε,λ,μ)；

（ⅱ）Su(ε,λ,μ)⊂(ε,λ,μ).

证明（ⅰ）事实上，设点x0∈Sl(ε,λ,μ)，假如存在点y∈T(μ)，满足则有

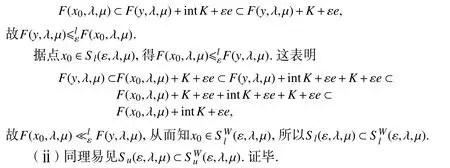
定义3设点e∈intK给定，ε ∈R+，D⊂X为非空凸子集，G:X→2Y{Ø}为给定非空集值映射：

（ⅰ）称G在D上为严格近似下K-凸的，假如对任何的点x1,x2∈D，满足x1≠x2，及任何的t∈(0,1)，有

（ⅱ）称G在D上为严格近似上K-凸的，假如对任何的点x1,x2∈D，满足x1≠x2，及任何的t∈(0,1)，有

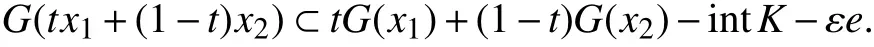
定义4[24-25]设T0,T1为拓扑线性空间，H:T0→2T1{Ø}为给定非空集值映射，点v0∈T0给定：

（ⅰ） 称H在点v0处为上半连续的，假如对H(v0)的任何邻域V1⊂T1，存在点v0的邻域V0⊂T0，对任何的点v∈V0，有H(v)⊂V1.

（ⅱ） 称H在点v0处为下半连续的，假如对任何的点u∈H(v0)，及点u的任何邻域V1⊂T1，存在点v0的邻域V0⊂T0，对任何的点v∈V0，有H(v)∩V1≠Ø.

（ⅲ） 称H在T0上为上（下）半连续的，假如对任何的点v∈T0，H在点v处为上（下）半连续的.

（ⅳ） 称H在T0上为连续的当且仅当H在T0上既上半连续又下半连续.

引理1[24]设T0,T1为赋范线性空间，H:T0→2T1{Ø}为给定非空集值映射，点v0∈V0给定，则H在点v0处下半连续当且仅当对任何的序列{vn}⊂T0，vn→v0，以及对任何的点u0∈H(v0)，存在点un∈H(vn)，有un→u0.

引理2[25]设T0,T1为赋范线性空间，H:T0→2T1{Ø}为给定非空集值映射，点v0∈V0给定，且H(v0)⊂T1为紧子集，则H在点v0处上半连续当且仅当对任何的序列{vn}⊂T0，vn→v0，以及对任何的点un∈H(vn)，存在点u0∈H(v0)，以及{unk}⊂{un}，有unk→u0.

引理3设F:X×Λ×Ω →2Y{Ø},T:Ω →2X{Ø}为给定非空集值映射，并设点(ε,λ,μ)∈R+×Λ×Ω，x0∈T(μ),e∈intK给定：

（ⅰ）假如WMin(F(x0,λ,μ))≠Ø，则点x0为问题（PSOP）的弱l-最小近似解当且仅当不存在点x∈T(μ)，使得

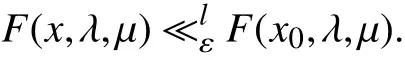
（ⅱ）假如WMax(F(x0,λ,μ))≠Ø，则点x0为问题（PSOP）的弱u-最小近似解当且仅当不存在点x∈T(μ)，使得

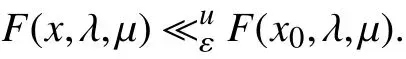
证明（ⅰ） 假如存在点x1∈T(μ)，使得则

这与（4）式矛盾，故结论得证.

（ⅱ） 类似于(ⅰ)的论证过程知结论(ⅱ)成立.证毕.

引理4设F:X×Λ×Ω →2Y{Ø},T:Ω →2X{Ø}为给定非空集值映射，并设点(ε,λ,μ)∈R+×Λ×Ω，e∈intK给定：

（ⅰ）假如F在X×Λ×Ω上为具非空紧值的严格近似下K-凸集值映射，T在 Ω上为非空凸集值映射，则

（ⅱ）假如F在X×Λ×Ω上为具非空紧凸值的严格近似上K-凸集值映射，T在 Ω上为非空凸集值映射，则

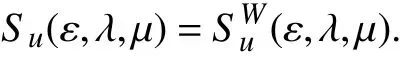
证明（ⅰ） 第1 步：据注3 的(ⅰ)知，Sl(ε,λ,μ)⊂(ε,λ,μ).

引理5设F:X×Λ×Ω →2Y{Ø},T:Ω →2X{Ø}为给定非空集值映射，并设点(ε,λ,μ)∈R+×Λ×Ω，e∈intK给定：

（ⅰ）假如F在X×Λ×Ω上为具非空紧值的上半连续集值映射，T在 Ω上为非空闭集值映射，则为闭集.

（ⅱ）假如F在X×Λ×Ω上为是非空紧值的下半连续集值映射，T在 Ω上为非空闭集值映射，则为闭集.

证明（ⅰ）设则必有点事实上易知点x0∈T(μ)，假如点据引理3 的(i)知，存在点y0∈T(μ)，使得则

再由引理2 知，存在点u0∈F(x0,λ,μ)，及{unk}⊂{un}，使得unk→u0，不失一般性，不妨假如un→u0.又据（9）式知，存在点v0∈F(y0,λ,μ)，使得

由（12）式得，当n充分大时，有un-v0∈intK+εe，这（11）式矛盾，故（10）式成立，因此，F(xn,λ,μ)，而这与xn∈(ε,λ,μ)矛盾，故点x0∈(ε,λ,μ).所以(ε,λ,μ)为闭集.

（ⅱ）类似于(i)的论证过程可知(ε,λ,μ)为闭集.证毕.

由文献[1]中的命题29 与命题30，易知：

引理6设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，并设点(ε,λ,μ)∈R+×Λ×Ω，e∈intK给定，又假如F在X×Λ×Ω上为具非空紧值上半连续集值映射，T在 Ω上为具非空紧值的集值映射，则Sl(ε,λ,μ)≠Ø.

据文献[1]中的推论24，易得：

引理7设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，并设点(ε,λ,μ)∈R+×Λ×Ω，e∈intK给定，又假如F在X×Λ×Ω上为非空紧值下半连续集值映射，T在 Ω上为具非空紧值的集值映射，则Su(ε,λ,μ)≠Ø.

2 问题（PSOP）近似解集与弱近似解集的上半连续性

本节讨论问题（PSOP）近似解集与弱近似解集的上半连续.

定理1设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧值；

（ⅱ）T(·)在点 μ0处连续且T(μ0)⊂X为非空紧子集成立，则：

（ⅱ）(·,·,·)在点(ε0,λ0,μ0)处是上半连续的.

证明（ⅰ）假如(·,·,·)在点(ε0,λ0,μ0)处不是上半连续的，则存在(ε0,λ0,μ0)的邻域V0，使得对点(ε0,λ0,μ0)的任何邻域Vε0×Vλ0×Vμ0⊂R+×Λ×Ω，存在点(ε0，λ0,μ0)∈Vε0×Vλ0×Vμ0，使得(ε0,λ0,μ0)⊄V0.因此，存在序列{(εn,λn,μn)}⊂Vε0×Vλ0×Vμ0，满足(εn,λn,μn)→(ε0,λ0,μ0)，使得对任何的n∈N，有(εn,λn,μn)⊄V0，则存在点

由T(·)在点 μ0处的上半连续性及xn∈T(μn)，并结合引理2 知，存在点x0∈T(μ0)，及子列{xnk}⊂{xn}，使得xnk→x0.不失一般性，不妨设xn→x0，则必有点事实上，假如点据引理3 的(i)及注1 的(ii)知，存在点x0∈T(μ0)，使得则

事实上，假如（16）式不成立，则存在子列{xnk}⊂{xn},{ynk}⊂{yn}，子列{(εnk,λnk,μnk)}⊂{(εn,λn,μn)}，使得F(xnk,λnk,μnk)⊄F(ynk,λnk,μnk)+intK+εnke，不失一般性，不妨假如成立F(xn,λn,μn)⊄F(yn,λn,μn)+intK+εne，于是存在点vn∈F(xn,λn,μn)，使得

据引理2 知，存在点v0∈F(x0,λ0,μ0)，及子列{vnk}⊂{vn}，有vnk→v0，不失一般性，设vn→v0.由（15）式知，存在点u0∈F(y0,λ0,μ0)，使得

再据引理1 得，存在点un∈F(yn,λn,μn)，使得un→u0.结合（18）式知，当n充分大时，有vn-un∈intK+εne，这与（17）式矛盾.

（ⅱ）类似可证：(·,·,·)在点(ε0,λ0,μ0)处是上半连续的.证毕.

定理2设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似下K-凸的；

（ⅲ）T(·)在点 μ0处连续且T(μ0)⊂X为非空紧凸子集

成立，则Sl(·,·,·)在点(ε0,λ0,μ0)处是上半连续的.

证明据引理4 的（ⅰ）知，对Sl(ε0,λ0,μ0)的任何邻域V0，则V0为的邻域，据定理1 知，(·,·,·)在点(ε0,λ0,μ0)处为上半连续的，则存在点(ε0,λ0,μ0)的邻域Vε0×Vλ0×Vμ0⊂R+×Λ×Ω，使得

因此，Sl(·,·,·)在点(ε0,λ0,μ0)处是上半连续的.证毕.

据引理4 的（ⅱ），并结合注3 的（ⅱ），类似定理2 的论证过程可知：

定理3设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧凸值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似上K-凸的；

（ⅲ）T(·)在点 μ0处连续且T(μ0)⊂X为非空紧凸子集；

成立，则Su(·,·,·)在点(ε0,λ0,μ0)处是上半连续的.

3 问题(PSOP)近似解集与弱近似解集的下半连续性

本节研究问题(PSOP)近似解集与弱近似解集的下半连续.

定义5设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为给定非空集值映射，对任意的点(ε,λ,μ)∈R+×Λ×Ω.

（ⅰ）定义集值映射Ql:R+×Λ×Ω×X→2X{Ø}为

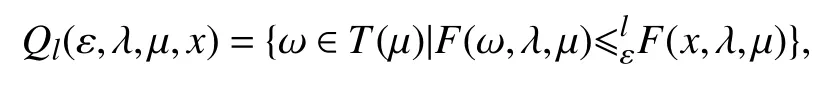
称Ql在R+×Λ×Ω×X上为下水平集值映射.

（ⅱ）定义集值映射Qu:R+×Λ×Ω×X→2X{Ø}为

称Qu在R+×Λ×Ω×X上为上水平集值映射.

注4据定义2 与定义5 易见，对任何的点(ε,λ,μ)∈R+×Λ×Ω，及x∈T(μ)，有：

（ⅰ）Sl(ε,λ,μ,Ql(ε,λ,μ,x))⊂Sl(ε,λ,μ,T(μ))；

（ⅱ）Su(ε,λ,μ,Qu(ε,λ,μ,x))⊂Su(ε,λ,μ,T(μ)).

引理8设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定，F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似下K-凸的且具非空紧值，设点x0∈Sl(ε0,λ0,μ0)，则Ql(ε0,λ0,μ0,x0)={x0}.

证明易知点x0∈Ql(ε0,λ0,μ0,x0).

另一方面，假如存在点x1∈Ql(ε0,λ0,μ0,x0)，满足x1≠x0，据集值映射F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似下K-凸的，则对任何的t∈(0,1)，有

类似引理8 的论证过程，并结合注1 的(i)，易知：

引理9设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定，F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似上K-凸的且具非空紧凸值，设点x0∈Su(ε0,λ0,μ0)，则Qu(ε0,λ0,μ0,x0)={x0}.

引理10设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧值；

（ⅱ）T(·)在点 μ0处连续且T(μ0)⊂X为非空紧子集

成立，则：

（ⅰ）Ql(·,·,·,·)在{ε0}×{λ0}×{μ0}×T(μ0)上是上半连续的；

（ⅱ）Qu(·,·,·,·)在{ε0}×{λ0}×{μ0}×T(μ0)上是上半连续的.

证明（ⅰ）假如存在点x0∈T(μ0)，使得Ql(·,·,·,·)在点(ε0,λ0,μ0,x0)处不是上半连续的，则存在Ql(ε0,λ0,μ0,x0)的邻域V0，使得对点(ε0,λ0,μ0,x0)的任何邻域Vε0×Vλ0×Vμ0×Vx0⊂R+×Λ×Ω×X，存在点(ε0,λ0,μ0,x0)∈Vε0×Vλ0×Vμ0×Vx0，使得

据T(·)在μ0处的上半连续性，及点ωn∈T(μn)，并结合引理2 知，存在点ω0∈T(μ0)，及{ωnk}⊂{ωn}，使得ωnk→ω0，不失一般性，不妨设ωn→ω0，则必有ω0∈Ql(ε0,λ0,μ0,x0).

事实上，对任何的点z∈F(x0,λ0,μ0)，据引理1 知，存在点zn∈F(xn,λn,μn)，使得zn→z，据（26）式知，

据F(·,·,·)在点(ω0,λ0,μ0)处的上半连续性及点yn∈F(ωn,λn,μn)，并结合引理2 知，存在点y0∈F(ω0,λ0,μ0)，及{ynk}⊂{yn}，满足ynk→y0，不失一般性，设yn→y0.据（28）式，当n→∞时，有

这表明点ω0∈Ql(ε0,λ0,μ0,x0)，则ωn→ω0∈V0，这与（27）式矛盾，因此，Ql(·,·,·,·)在 {ε0}×{λ0}×{μ0}×T(μ0)上是上半连续的.

（ⅱ）类似于对(i)的论证过程，易知Qu(·,·,·,·)在{ε0}×{λ0}×{μ0}×T(μ0)上是上半连续的.证毕.

定理4设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似下K-凸的；

（ⅲ）T(·)在点 μ0处连续具非空紧值且T(μ0)⊂X为紧凸子集成立，则：

（ⅰ）Sl(·,·,·)在点(ε0,λ0,μ0)处是下半连续的；

证明（ⅰ）假若Sl(·,·,·)在点(ε0,λ0,μ0)处不是下半连续的，则存在点x0∈Sl(ε0,λ0，μ0)，以及X中的零点的邻域V0，使得对点(ε0,λ0,μ0)的任何邻域Vε0×Vλ0×Vμ0⊂R+×Λ×Ω，存在点(ε0,λ0,μ0)∈Vε0×Vλ0×Vμ0，使得

故存在序列{(εn,λn,μn)}⊂Vε0×Vλ0×Vμ0，满足(εn,λn,μn)→(ε0,λ0,μ0)，使得

据引理1 及点x0∈T(μ0)知，存在点xn∈T(μn)，使得xn→x0.结合引理10 知，Ql(·,·,·,·)在点(ε0,λ0,μ0,x0)处是上半连续的，对Ql(ε0,λ0,μ0,x0)的邻域Ql(ε0,λ0，μ0,x0)+V0，存在n0∈N，当n＞n0时，有

又由引理8 知，Ql(ε0,λ0,μ0,x0)={x0}，并注意到（30）式，得

故点xn∈Ql(εn,λn,μn,xn)，则Ql(εn,λn,μn,xn)≠Ø.

可断言Ql(εn,λn,μn,xn)为闭的.事实上，设{ωn}⊂Ql(εn,λn,μn,xn),ωn→ω0，则点ωn∈T(μn)，且

据T(μn)为闭集知，点ω0∈T(μn)，对任何的点y∈F(xn,λn,μn)，由（32）式得，存在点yn∈F(ωn,λn,μn)，使得y-yn∈K+εne.再由F(·,·,·)在点(ω0,λ0,μ0)处的上半连续性及引理2 得，存在点y0∈F(ω0,λ0,μ0)，及{ynk}⊂{yn}，ynk→y0，不失一般性，不妨设yn→y0，结合K的闭性知，

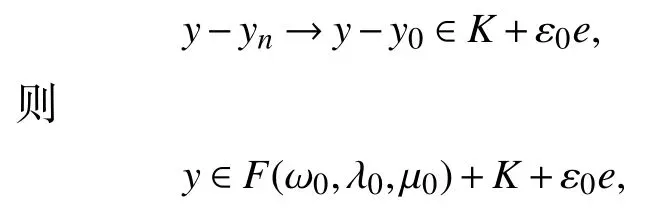
故F(xn,λn,μn)⊂F(ω0,λ0,μ0)+K+ε0e，这表明点ω0∈Ql(εn,λn,μn,xn)，从而知Ql(εn,λn,μn,xn)为闭集.

注意到T(μn)为闭集及Ql(εn,λn,μn,xn)⊂T(μn)，知Ql(εn,λn,μn,xn)为紧集，再结合引理6 知，Sl(εn,λn,μn,Ql(εn,λn,μn,xn))≠Ø.设点yn∈Sl(εn,λn,μn,Ql(εn,λn，μn,xn))，由（31）式及注4 的(i)知，

这与（29）式矛盾，故Sl(·,·,·)在点(ε0,λ0,μ0)处是下半连续的.

由引理4 的(ⅱ)，引理7，引理9，引理10，结合注3 的(ii)和注4 的(ii)，类似定理4 的论证过程可知：

定理5设F:X×Λ×Ω→2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧凸值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似上K-凸的；

（ⅲ）T(·)在点 μ0处连续具非空紧值且T(μ0)⊂X为紧凸子集

成立，则：

（ⅰ）Su(·,·,·)在点(ε0,λ0,μ0)处是下半连续的；

（ⅱ）(·,·,·)在点(ε0,λ0,μ0)处是下半连续的.

据定理1 的(i)，定理2 及定理4 知：

定理6设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似下K-凸的；

（ⅲ）T(·)在点 μ0处连续具非空紧值且T(μ0)⊂X为紧凸子集

成立，则：

（ⅰ）Sl(·,·,·)在点(ε0,λ0,μ0)处是连续的；

由定理1 的(ii)，定理3 及定理5 知：

定理7设F:X×Λ×Ω →2Y{Ø}，T:Ω →2X{Ø}为非空集值映射，且点(ε0,λ0,μ0)∈R+×Λ×Ω，e∈intK给定.又假如：

（ⅰ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上连续且具非空紧凸值；

（ⅱ）F(·,·,·)在T(μ0)×{λ0}×{μ0}上为严格近似上K-凸的；

（ⅲ）T(·)在点 μ0处连续具非空紧值且T(μ0)⊂X为紧凸子集成立，则：

（ⅰ）Su(·,·,·)在点(ε0,λ0,μ0)处是连续的；

4 结语

在赋范线性空间中研究了含参集值优化问题近似解集和弱近似解集的上半连续性和下半连续性.

（ⅰ）引入含参集值优化问题近似解与弱近似解的概念，给出近似解与弱近似解的基本性质关系.

（ⅱ）在目标函数映射具有广义锥凸性，借助水平映射技巧，建立了含参集值优化问题近似解集与弱近似解集的上半连续性和下半连续性的充分性定理.

（ⅲ）沿用本文研究含参集值优化问题近似解集与弱近似解集半连续的基本思想，结合改进集的概念及性质，可进一步讨论基于改进集的参数集值优化问题近似解集与弱近似解集映射的Berge 连续性、Hausdorff 连续性等，且研究成果可为探索参数集值优化问题各类解的Hölder 连续性、Lipschitz 连续性、紧闭性、连通性、适定性及算法设计等提供理论借鉴.