国内调节效应的方法学研究*
方 杰 温忠麟 欧阳劲樱 蔡保贞
国内调节效应的方法学研究*
方 杰1温忠麟2欧阳劲樱2蔡保贞2
(1广东财经大学新发展研究院/应用心理学系, 广州 510320) (2华南师范大学心理学院/心理应用研究中心, 广州 510631)
在心理学和其他社科研究领域, 大量实证文章建立调节效应模型, 以分析自变量对因变量的影响是如何随着调节变量的变化而改变。过去10多年, 调节效应分析成了方法学研究的一个热点。从显变量的调节效应、潜变量的调节效应、多层数据的调节效应、基于两层回归模型的单层调节分析、纵向数据的调节效应、调节和中介的整合模型六个主题系统地总结了国内调节效应分析的方法学研究的发展历程。最后对调节效应的未来研究方向做了讨论和拓展。
调节效应, 潜变量, 类别变量, 多层数据, 纵向数据
调节效应(moderating effect)是社会科学研究中的一个重要概念, 在分析多个变量之间关系时经常碰到。当自变量与因变量的关系受到第三个变量的影响时, 变量称为调节变量(见图1(a))。调节变量既可能影响与之间关系的方向, 也可能影响关系的强度(Baron & Kenny, 1986)。20世纪90年代, 随着(Aiken & West, 1991)一书的出版, 调节效应分析逐渐得到研究者的重视, 成为社科研究中最常用的分析方法之一。在国内, 温忠麟等(2003, 2005)率先介绍了显变量和潜变量的调节效应分析方法, 引领和推动了国内调节效应的方法研究和应用。此后, 调节效应分析成了国内心理统计的一个研究热点(温忠麟等, 2021)。
以中国知网(https://www.cnki.net/)全文数据库为数据源, 以关键词和主题词检索调节变量、调节效应、调节作用、潜调节、潜变量调节、交互效应、交互作用、潜交互、潜变量交互、有中介的调节、有调节的中介, 检索2001年至2021年期间国内发表的有关调节(交互)效应的方法学研究论文, 得到符合要求的方法文章27篇:《心理学报》9篇, 《心理科学进展》4篇, 《心理科学》3篇, 《心理学探新》2篇, 《数理统计与管理》2篇, 《统计与决策》2篇, 《管理学报》1篇, 《管理科学》1篇, 《中国卫生统计》1篇, 《数理医药学杂志》1篇, 《数学的实践与认识》1篇。
国内的调节效应方法学研究论文可以分为6个主题:显变量的调节效应、潜变量的调节效应、多层数据的调节效应、基于两层回归模型的单层调节分析、纵向数据的调节效应、调节和中介的整合模型(包括有调节的中介和有中介的调节模型)。表1按主题列出了调节效应方法研究的由远及近的文献(共27篇, 另有5篇为印刷中), 其中第一篇文献为相应主题在国内的首个研究。本文首先简介调节效应模型, 接着对每个主题逐一做系统回顾(其中调节和中介的整合模型详见温忠麟和方杰等(2022)关于国内中介效应的方法学研究的综述文章, 这里只做统计, 不再赘述), 同时也兼顾国际上的相关研究。最后讨论了调节效应的未来研究方向。
1 显变量的调节效应分析
当和Z都是连续变量时, 调节效应可以通过下面回归方程进行分析(图1(b)是相应的路径图),

表1 国内调节效应的方法学研究文献一览
注:温忠麟和欧阳劲樱等(2022)于2021年11月25日在中国知网在线发表。SEM表示结构方程模型, LMS表示潜调节结构方程法, RCP表示随机系数预测法, MLM表示多层模型, CLM表示交叉滞后模型, LGM表示潜变量增长模型。
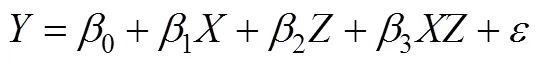
如果回归系数3显著, 就表示调节效应显著。当调节效应显著时, 研究者常将方程(1)重写可得方程(2),
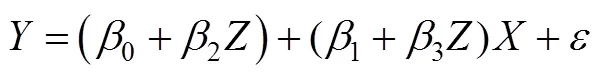

图1 调节效应模型图(改编自: 方杰等, 2015)
显变量的调节效应研究主要从变量的中心化、标准化解、简单斜率检验、类别变量的调节效应分析四个方面展开。
1.1 变量的中心化的作用
方杰等人(2015)回顾了均值中心化在调节效应分析中的作用。对自变量和调节变量进行均值中心化(即变量减去样本均值), 不能减少自变量和调节变量之间的多重共线性, 也不会影响乘积项(即调节效应)的检验。中心化能减少的是和之间、和之间的多重共线性, 会影响和的回归系数。中心化的意义还在于改善对结果的理解。中心化后, 变量的原点移到了样本均值的位置, 这时回归系数1和2都有了明确的意义。系数1反映了为均值时对的影响, 系数2反映了为均值时对的影响(方杰等, 2015; 刘红云, 2019; 温忠麟, 刘红云, 2020)。
1.2 标准化解
标准化的系数估计对比较调节效应大小有重要作用。如果使用原始变量或中心化后的变量产生乘积项, 再进行调节效应分析, 则SPSS软件得到的标准化估计值并不是调节效应的标准化解。此外, 如果将自变量和调节变量先相乘得到乘积项, 然后再对乘积项进行标准化, 这样得到的调节效应估计值也不是标准化解(温忠麟等, 2008)。正确做法是, 先处理缺失值, 确保所有变量的数据都是完整数据, 然后将所有变量都标准化(Z、Z和Z), 接着再产生乘积项ZZ, 调节效应检验的方程(1)变为

1.3 简单斜率检验
简单斜率检验的零假设为H0:1+3Z = 0, 如果检验的结果是拒绝零假设, 则表明简单斜率1+3Z显著(不等于0)。研究者通常采用选点法(pick-a-point approach)和Johnson-Neyman法(简写为J-N法)进行简单斜率的显著性检验(方杰等, 2015; 温忠麟, 刘红云, 2020)。
1.3.1 选点法
选点法是先选点, 即固定调节变量的若干值(常选均值、均值 ± 标准差), 然后利用如下统计量
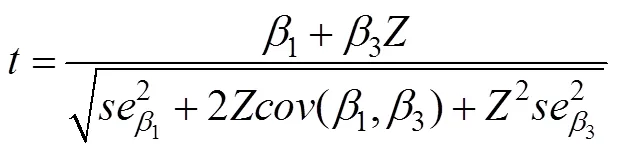

1.3.2 J-N法
目前, J-N法的简单斜率检验和简单斜率图(图2(b))已可以利用SPSS宏PROCESS (Hayes, 2018)、软件(Muthén & Muthén, 1998/2017, 程序见附录)、R软件(Preacher et al., 2006)、Excel 2013 (Carden et al., 2017)完成。J-N法在常用统计软件上的实现, 极大地促进了J-N法的实际应用。
当调节变量为连续变量时, 选点法一次只能检验一个点(调节变量的某个取值)的简单斜率的显著性, 而J-N法能在[min,max]中寻找简单斜率显著的的取值区间(方杰等, 2015), 所以J-N法的输出结果中包含了选点法的检验结果。除非研究者对某个调节变量值感兴趣时才使用选点法, 否则使用J-N法较好。
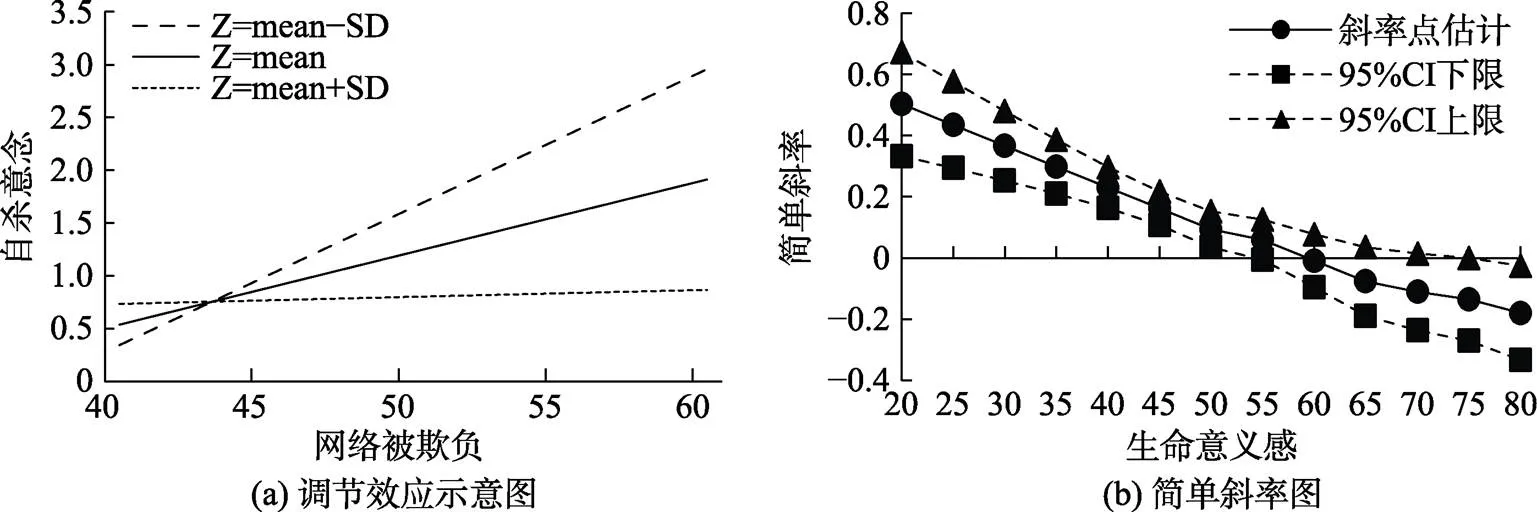
图2 调节效应的简单斜率检验图(改编自:罗畏畏等, 2018)
1.3.3 关于展示调节效应的画图
调节效应图(图2(a))和简单斜率图(图2(b))虽然都反映了调节作用, 但两个图的横轴和纵轴都不同。图2(a)反映了与之间关系如何随调节变量的变化而变化, 但是不能看出简单斜率是否显著; 而图2(b)反映了简单斜率1+3Z如何随的变化而变化, 如果简单斜率的95%置信区间(图中双曲线作为上下限)不包含0, 就表示简单斜率显著, 否则简单斜率不显著。如果不受篇幅限制, 可以将图2(a)和图2(b)都呈现出来, 否则通常只呈现图2(a)。
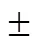
1.4 类别变量的调节效应分析
类别变量的调节效应分析(因变量是连续变量)分三种情况。第一种, 如果自变量和调节变量都是类别变量, 则进行方差分析, 此时调节效应就是交互效应, 调节效应量用2或偏2表示, 简单斜率检验就是简单主效应检验(温忠麟等, 2005; 温忠麟, 刘红云, 2020)。第二种, 如果自变量和调节变量中有一个为二分类别变量, 另一个是连续变量, 仍可使用层次回归进行调节效应分析(温忠麟等, 2005)。第三种, 如果自变量或调节变量为个类别(≥3), 问题就变得复杂。
以3类别自变量(调节变量和因变量为连续变量)为例, 类别变量的调节效应分析步骤如下(方杰, 温忠麟, 印刷中a)。
第一步, 将多类别自变量进行虚拟编码(dummy coding)。3类别的自变量将产生2个虚拟变量1和2。参考类别的编码为1=2= 0, 类别2编码为1= 1且2= 0, 类别3编码为1= 0且2= 1。
第二步, 用带有乘积项的回归模型做层次回归分析。先让自变量和调节变量进入回归方程:
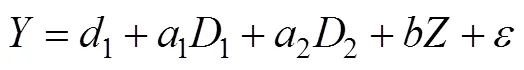
再让乘积项进入回归方程:
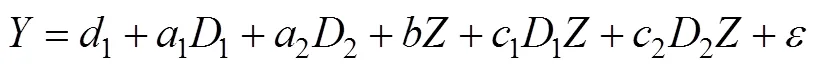
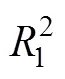
第三步, 简单斜率检验。1+1Z和2+2Z表示简单斜率, 只需要将公式(4)中的1和3换成1和1(或2和2), 就能进行选点法的简单斜率检验。当使用PROCESS进行调节效应分析时, 可将1作为自变量,2和2×作为协变量, 即可得到J-N法的简单斜率检验结果(方杰, 温忠麟, 印刷中a)。
如果是多类别调节变量(自变量和因变量为连续变量)的调节效应分析, 有如下两种方法。第一, 采用多类别自变量的分析步骤进行调节效应分析。如果想得到标准化解, 只需将自变量和因变量标准化即可(刘红云, 2019)。第二, 分组回归法。按调节变量的类别对被试分组, 在每组内作对的线性回归分析, 然后检验这些回归系数两两之间是否相等。以三个类别的调节变量为例, 则需要检验3次, 检验公式见温忠麟和刘红云(2020)。如果不全相等, 则表示调节效应显著。分组回归法的不足在于, 只能知道调节效应是否显著, 不能估计调节效应的效应量Δ2(温忠麟, 刘红云, 2020)。而且多次检验增加第I类错误率, 比较好的做法是做结构方程模型的多组比较(见下一节)。
2 潜变量的调节效应分析
潜变量的调节效应分析可分为两类, 一类是自变量为潜变量、调节变量为类别变量, 另一类是自变量和调节变量都是潜变量。
2.1 调节变量为类别变量
当自变量为潜变量, 调节变量为类别变量时, 一般使用多组结构方程模型(侯杰泰等, 2004), 它是分组回归的推广(温忠麟, 刘红云, 2020)。多组结构方程模型的原理是, 将各组的回归系数约束为相等, 与无约束的模型相比, 如果模型拟合明显变差(用卡方差异检验进行判断), 则说明调节效应显著。多组结构方程模型的调节分析包含三个步骤的检验:结构不变性检验、弱不变性检验和回归系数的不变性检验, 可以使用软件编程实现(参见:刘红云, 2019)。这种方法的不足主要有以下三点(刘红云, 2019; 温忠麟, 刘红云, 2020)。第一, 会提高第Ⅱ类错误率, 检验力降低。第二, 该方法只能检验调节效应是否显著, 无法估计调节效应的大小。第三、该方法受样本容量的限制, 即分组后的子样本可能太小。
2.2 调节变量为潜变量
温忠麟等(2003)率先介绍潜变量调节效应, 并评述了潜变量调节效应分析的4种方法, 包括两种回归方法——使用潜变量的因子得分进行回归分析和两步最小二乘回归, 以及两种结构方程方法——多组结构方程模型和带有潜变量乘积项的结构方程模型。温忠麟和侯杰泰(2004)通过一个实例对上述4种方法进行了比较, 结果表明两种结构方程模型方法优于两种回归方法, 精确度较高。此外, 还有研究者介绍了两步最小二乘回归在SAS上的实现(李建明, 曲成毅, 2011), 有约束的乘积指标法在LISREL (李建明, 曲成毅, 2007; 付会斌等, 2010)和SAS上的实现(吴冰, 王重鸣, 2010)。
带有潜变量乘积项的结构方程模型是潜变量调节效应方法研究的重心。可以分为三个方面:模型简化、分析方法比较和标准化解。
2.2.1 模型简化
带有潜变量乘积项的结构方程模型最先使用的建模方法是乘积指标法(product indicator approaches), 使用指标的乘积作为潜变量乘积项的指标。Kenny和Judd (1984)首创的乘积指标法模型需要繁琐的非线性约束等式, 称为有约束的乘积指标法。
模型简化主要针对乘积指标法, 包括两个方面的研究, 一是从约束模型到无约束模型, 二是从有均值结构到无均值结构。有约束的乘积指标法经历了从Kenny-Judd模型(1984)、Jöreskog- Yang模型(1996)到Algina-Moulder模型(2001)的演化, 其中Algina-Moulder模型(自变量的指标是中心化的, 结构方程带有均值结构)是最优的, Algina-Moulder模型的分析方法简称为约束方法。约束方法一是复杂, 难以应用; 二是稳健性差, 因为有的约束等式需要有正态性假设才成立。Marsh等(2004)提出了无约束模型, 取消了全部非线性约束, 模型得到简化。通过模拟研究发现, 在潜调节效应分析中, 无约束方法在正态情形下与约束方法相当, 在非正态情形下比约束方法表现更优。
将所有指标先中心化, 指标的均值为零, 但乘积项的均值不为零, 这就是潜变量调节效应模型中均值结构产生的根源(吴艳等, 2009)。解决方案就是将乘积项的均值变为0, 具体做法就是在所有指标中心化的基础上产生乘积指标, 并将乘积指标再次中心化, 即双重中心化(吴艳等, 2009; Lin et al., 2010)。值得注意的是, 在实际使用中, 将所有指标中心化就可以建模了, 并不需要将乘积指标再次中心化(温忠麟, 吴艳, 2010)。因此, 建议将所有指标先中心化, 用无约束方法建立无均值结构的潜变量调节效应模型(吴艳, 2009)。
2.2.2 分析方法
除了乘积指标法, 温忠麟等(2012, 2013)介绍了无需乘积指标的潜变量调节效应分析方法, 包括贝叶斯法(Bayesian approaches, Lee et al., 2007)、潜调节结构方程法(Latent Moderated Structural Equations, LMS, Klein & Moosbrugger, 2000)和准极大似然估计法(Quasi-Maximum Likelihood, QML, Klein & Muthén, 2007)。温忠麟等(2013)还提供了潜调节结构方程法分析潜变量调节效应的程序。
比较和选择估计方法是潜变量调节效应理论研究的重要组成部分。已有研究结果发现, 在正态或偏态很小的情形, 无约束乘积指标模型在样本容量较大时可以使用, 而LMS的表现相对更好, 在小样本时估计偏差和标准误偏差也可以忽略, 且检验力更高(Cham et al., 2012; Jackman et al., 2011; Marsh et al., 2004)。而在非正态情形, 无约束乘积指标模型比较稳健, 在大样本时可以使用, 而LMS对非线性效应及其标准误的估计有偏, 且比无约束乘积指标模型的第Ⅰ类错误率更高(Cham et al., 2012; Kelava & Nagengast, 2012; Marsh et al., 2004; Wu et al., 2013)。QML的表现与LMS的类似, 但至今尚未在常用的结构方程软件中实现, 限制了该方法的应用。
2.2.3 标准化解
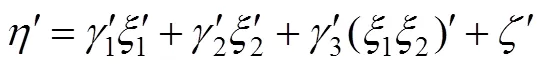


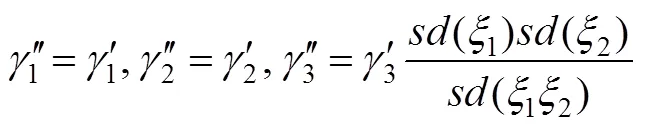
温忠麟团队进一步证明了恰当标准化解的尺度不变性, 即使用不同单位的数据, 最后得到的标准化估计是相同的(Wen et al., 2010)。吴艳等(2011)推导出无均值结构的标准化模型, 其标准化解与前述的一致。吴艳等(2014)还提出用Bootstrap方法计算恰当标准化估计的标准误和值, 从而对恰当标准化估计进行显著性检验。
对于恰当标准化估计, 温忠麟和欧阳劲樱等(2022)比较了无约束乘积指标法、LMS和贝叶斯法。结果表明, 如果数据是正态分布, 推荐使用LMS法。如果数据是非正态的, 则无约束乘积指标法比较稳健, 但需要较大的样本(不小于500); 在小样本且外生潜变量之间相关较低时(可以通过验证性因子分析去估计和检验), 考虑使用(无信息先验的)贝叶斯法。他们还提供了无约束乘积指标法分析潜变量调节效应的程序, 可以直接产生标准化估计。相应的LMS和贝叶斯法的程序参见温忠麟和刘红云(2020)。
3 多层数据的调节效应分析
前两个主题都讨论的是单层数据。在心理、教育和管理等社科研究中, 经常遇到多层(嵌套)数据, 如学生嵌套于班级或学校、员工嵌套于公司、居民嵌套于社区等。多层数据的调节效应模型发展经历了三个阶段, 第一阶段是混淆的多层调节效应, 第二阶段是无混淆的多层调节效应, 第三阶段是多层结构方程的调节效应。
3.1 混淆的多层调节效应模型
以员工嵌套于公司为例, 最常见的多层数据的调节效应模型可表示为
层1 :

层2:
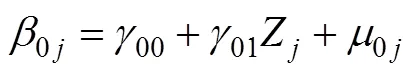


其中, 调节项为XZ, 调节效应的大小由回归系数11表示, 如果回归系数11显著不为0, 则表示调节效应显著, 简单斜率为10+11Z(方杰等, 2018)。应用研究者可利用网络工具(http://www. quantpsy.org/interact/hlm2.htm下载)进行选点法的简单斜率检验(Preacher et al., 2006), 利用软件(Muthén & Muthén, 1998/2017)进行J-N法的简单斜率检验。这种方法的不足在于, 主效应10没能区分X的组内和组间效应, 调节效应11没能区分跨层调节和层2调节效应, 因此方程(11)~ (13)称为混淆的多层调节效应模型(方杰等, 2018)。
3.2 无混淆的多层调节效应模型

层1:
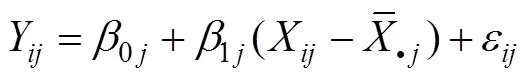
层2:


将方程(13)、(16)代入方程(15)得:
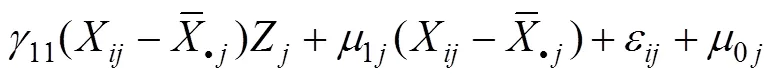
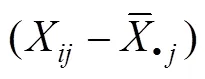
3.3 多层结构方程的调节效应模型
值得注意的是, 多层结构方程模型的调节效应分析存在计算耗时较多和数据收敛困难的问题。可行的解决方法有以下三种。第一, 如果研究模型既包括跨层调节, 又包括同层调节, 则可尝试将随机系数预测法和潜调节结构方程法混合使用(方杰等, 2018)。第二, 将多层线性模型的调节效应分析结果当成多层结构方程的调节效应分析的初始值(方杰等, 2018)。第三, 可将贝叶斯法和潜调节结构方程法相互结合进行调节效应分析(Asparouhov & Muthén, 2021)。
4 基于两层回归模型的单层调节分析
虽然调节效应分析大多使用线性回归的方法(见方程(1))进行分析, 但线性回归的调节效应分析存在一些不足, 借助两层回归模型进行调节效应分析有明显的优势, 可以弥补这些不足。
对于单层数据, 使用线性回归的方法(见方程(1))进行调节效应分析存在如下三个不足(方杰, 温忠麟, 2022a):第一, 多元回归法将图1()的调节效应(moderation)模型人为的变换成1()的交互效应(interaction)模型。因此方程(1)其实是检验与的交互效应是否显著, 并没有直接对图1()的调节效应模型进行检验。在调节效应中, 哪个是自变量, 哪个是调节变量, 是很明确的, 有强有力的理论支持的, 在一个确定的模型中两者不能互换。但在交互效应里, 两个自变量地位是对称的, 可以互换的, 即如果对的效应受到的调节(此时是自变量), 那么对的效应同样也受到的调节(此时是调节变量), 且方程(1)对两种调节效应的分析结果相同(温忠麟, 刘红云, 2020)。第二, 多元回归假设误差方差齐性(即当自变量取不同的值x时, 误差方差相等), 但这个假设在调节效应分析中难以满足。第三, 调节效应量指标Δ2存在不足。Δ2并没有直接测量调节变量对→关系的调节程度, Δ2反映的是乘积项对因变量的方差的额外解释力。温忠麟和叶宝娟(2014)认为Δ2变化要超过2%才有实质性意义, 但Δ2的数值往往很小。
一种改进方法是借助两层回归模型去分析单层数据。两层回归模型可表示为(方杰, 温忠麟, 2022a):
层1:

层2:


基于两层回归模型对单层数据进行调节效应分析存在明显的优势:第一, 两层回归模型中, 调节变量Z直接解释了自变量X和因变量Y的关系(即0i和1i), 更符合调节效应的定义; 第二, 两层回归模型能清楚地区分自变量X和调节变量Z的作用, 自变量X在层1方程中, 作用是解释因变量Y的方差; 调节变量Z却只能在层2方程中, 作用是解释0i和1i的方差; 第三, 两层回归模型不需要误差方差齐性的假设, 因为两层回归模型的误差方差本来就是异方差的; 第四, 两层回归模型的调节效应量是
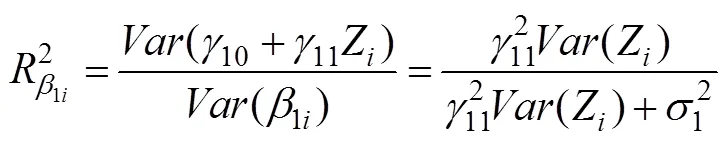
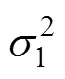
5 纵向数据的调节效应分析
纵向数据的调节效应分析包括三种类型。第一类是在自变量、调节变量和因变量中, 仅对因变量进行重复测量。第二类是仅有自变量和因变量两个变量, 两个变量都进行重复测量。第三类是自变量、调节变量和因变量都进行重复测量。
5.1 一个变量是纵向数据的调节效应分析
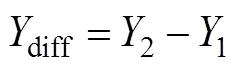
5.2 两个变量是纵向数据的调节效应分析
自变量和因变量都是纵向数据的调节效应分析, 可用交叉滞后模型(或称自回归模型)进行分析。交叉滞后模型的调节效应检验可表示为(Ozkok et al., in press)
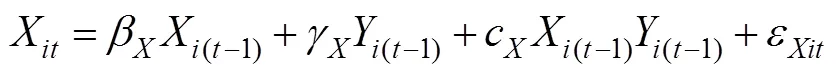

其中, 下标表示个体, 系数β和β表示自回归效应(即每个变量前后时间点的效应), 系数γ和γ表示滞后效应(即每个变量对前因变量的回归)。调节项是X(t–1)Y(t–1), 如果系数c和(或) c显著不为0, 则表示调节效应显著。值得注意的是, 自回归系数、滞后系数和调节系数的下标都没有时间, 表示自回归效应、滞后效应和调节效应在不同时间点都具有稳定性(目的是简化模型)。ε和ε表示误差项, 服从正态分布。交叉滞后模型中的调节效应至少有两个意义(以c为例进行说明)。第一,X(t-1)调节了滞后效应Y(t-1)→X。第二,Y(t-1)调节了自回归效应X(t-1)→X。总之, 交叉滞后模型可以考察具有时间先后关系的变量间的调节效应, 这是交叉滞后模型的一大特色。Ozkok等(in press)考察了时刻1的工作−家庭冲突(X1)对时刻1的工作满意度(Y1)和时刻2的工作满意度(Y2)之间的滞后效应的调节作用。并提供了交叉滞后模型分析纵向数据的调节效应的程序(使用潜调节结构方程法)。
5.3 三个变量是纵向数据的调节效应分析
5.3.1 基于多层模型的调节效应分析
纵向(追踪)数据可看成是一个两层的层级结构, 重复测量或测量点为第1层级, 观测个体为第2层级, 可使用多层模型进行纵向数据的调节效应分析。基于多层模型的纵向数据的调节效应分析可表示为:
层1:

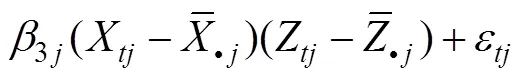
层2:

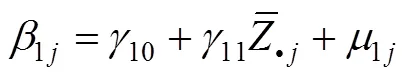
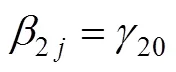
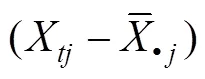
5.3.2 基于潜变量增长模型的调节效应分析

6 结语
本文从显变量的调节效应、潜变量的调节效应、多层数据的调节效应、基于两层回归模型的单层调节分析、纵向数据的调节效应、调节和中介的整合模型6个主题系统地总结了国内调节效应的方法学研究的发展(同时也兼顾了这些方面国际上的相关研究), 可作为读者了解调节效应分析的文献导读。
调节效应分析的发展呈现出两个鲜明的特点。第一, 调节效应分析的发展存在两条主线:一条主线是显变量的调节发展到潜变量的调节; 另一条主线是调节效应分析所适用的数据类型的发展, 即从连续数据发展到类别数据, 从单层数据发展到多层(水平)数据, 从截面(横向)数据发展到追踪(纵向)数据。
第二, 国内学者在调节效应分析方法研究领域贴近国际先进水平, 有些方面还做出了领先的贡献。温忠麟团队在潜变量调节效应分析方面的系列研究成果(Marsh et al., 2004, 2007; Lin et al., 2010; Wen et al., 2010, 2014; Wu et al., 2013; 温忠麟等, 2008, 2013; 温忠麟, 欧阳劲樱等, 2022; 吴艳等, 2009, 2011)推动和引领了潜变量调节效应分析在国际和国内的发展, 特别是关于潜变量调节效应模型的标准化解方面的研究, 产生了深远的影响, 标准化解的公式已被8.2及以上版本采用。刘红云团队的系列相关研究成果(Liu et al., 2020, in press; Liu & Yuan, 2021; 刘红云等, 2021)推动了基于两层回归模型的调节效应分析的发展:从显变量发展到潜变量(Liu et al., 2020), 从简单调节效应模型发展到有调节的中介模型(Liu et al., in press)和有中介的调节模型(刘红云等, 2021), 并且对调节效应量做了推广(Liu & Yuan, 2021)。
调节效应分析方法领域的国际前沿有如下三个发展趋势。第一, 潜调节结构方程法和贝叶斯法的结合在8.2及其以上版本的实现, 不仅可以显著减少潜调节结构方程法的运行时间, 并且模拟研究发现, 在多层调节效应分析中, 贝叶斯估计的潜调节结构方程法的表现优于极大似然估计的潜调节结构方程法(Asparouhov & Muthén, 2021)。
第二, 本文主要讨论了一个自变量和一个调节变量的调节效应, 多个变量的调节效应分析是最新的发展方向。例如, 根据调节变量之间是否存在相互影响, 可以分为有调节的调节模型(图3(a))和并行多重调节模型(图3(b)) (方杰, 温忠麟, 印刷中a)。更进一步, Serang等(2017)提出了探索性中介分析方法, 利用Lasso法从一系列候选的中介变量中识别出真正有效的中介变量, “有效”是指特定路径的中介效应显著不为0。那么, 如何进行探索性调节效应分析, 从一系列候选的调节变量中识别出真正有效的调节变量呢?这个问题还有待深入研究。
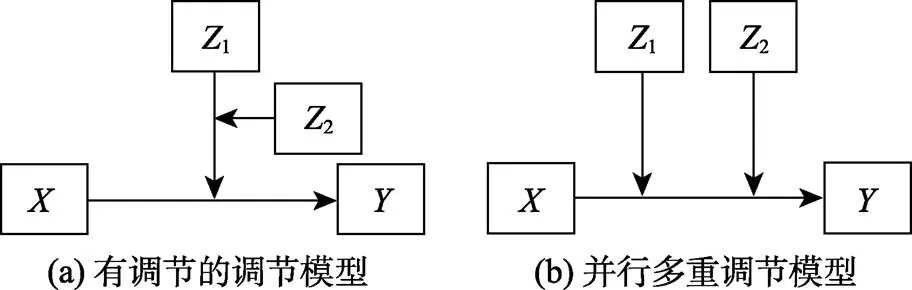
图3 两个调节变量的调节模型(改编自Hayes, 2018)
第三, 纵向数据的调节效应分析是一个新的研究热点。例如, 像方程(22)和(23)所示的模型考察的是混淆的调节效应, 即随时间变化的个体内部分和不随时间变化的个体间部分混在一起, Ozkok等(in press)利用随机截距的交叉滞后分析的原理(见:刘源, 2021), 提出了无混淆的调节效应分析方法。又如, McNeish和Hamaker (2020)展示了如何用动态结构方程模型进行密集追踪数据(重复测量次数≥10)的调节效应分析, 这种模型本质是在多层模型中添加自回归效应和滞后效应(郑舒方等, 2021)。
调节效应模型的发展有力地推动了调节效应的应用。相信随着调节效应分析方法研究的深入, 会不断加深我们对调节效应问题的理解。
董维维, 庄贵军, 王鹏. (2012). 调节变量在中国管理学研究中的应用.(12), 1735–1743.
方杰, 温忠麟. (2018). 基于结构方程模型的有调节的中介效应.,(2), 453–458.
方杰, 温忠麟. (2022a). 基于两水平回归模型的调节效应分析及其效应量.(5), 1183–1190.
方杰, 温忠麟. (2022b). 纵向数据的调节效应分析.
方杰, 温忠麟. (印刷中a). 两类常见的类别变量调节效应分析.
方杰, 温忠麟. (印刷中b). 有调节的多层中介效应分析.
方杰, 温忠麟, 梁东梅, 李霓霓. (2015). 基于多元回归的调节效应分析.(3), 715–720.
方杰, 温忠麟, 吴艳. (2018). 基于结构方程模型的多层调节效应.(5), 781–788.
方杰, 张敏强, 顾红磊, 梁东梅. (2014). 基于不对称区间估计的有调节的中介模型检验.,(10), 1660–1668.
付会斌, 孔丹莉, 潘海燕, 丁元林. (2010). 非线性结构方程模型的研究进展.(1), 101–103.
侯杰泰, 温忠麟, 成子娟. (2004).. 北京:教育科学出版社.
李艾, 李君文. (2008). 调节变量(moderator)辨析:类型、表述和识别.,(2), 257–264.
李建明, 曲成毅. (2007). 隐变量交互作用分析建模及其在SAS上的实现.(1), 31–37.
李建明, 曲成毅. (2011). 隐变量交互作用分析建模方法——两阶段最小二乘法(2SLS)及其在SAS软件上的实现.(6), 631–634.
廖卉, 庄瑗嘉. (2012). 多层次理论模型的建立及研究方法. 见陈晓萍, 徐淑英, 樊景立 (编).(第二版, pp. 442–476). 北京: 北京大学出版社.
刘红云. (2019).. 北京: 中国人民大学出版社.
刘红云, 袁克海, 甘凯宇. (2021). 有中介的调节模型的拓展及其效应量.,(3), 322–338.
刘源. (2021). 多变量追踪研究的模型整合与拓展:考察往复式影响与增长趋势.,(10), 1755–1772.
卢谢峰, 韩立敏. (2007). 中介变量、调节变量与协变量——概念、统计检验及其比较.,(4), 934–936.
罗畏畏, 方杰, 孙雅文. (2018). 网络被欺负与大学生自杀意念的关系及生命意义感的调节作用.,(4), 211–217.
乔元波, 王砚羽, 邹仁余. (2017). 非线性模型连续调节变量检验的实现方法., (9), 9–14.
王阳, 温忠麟, 王惠惠, 管芳. (2022). 第二类有中介的调节模型.(9), 2131−2142.
温忠麟, 方杰, 沈嘉琦, 谭倚天, 李定欣, 马益铭. (2021). 新世纪20年国内心理统计方法研究回顾.,(8), 1331–1344.
温忠麟, 方杰, 谢晋艳, 欧阳劲樱. (2022). 国内中介效应的方法学研究.,(8), 1692–1702.
温忠麟, 侯杰泰. (2004). 隐变量交互效应分析方法的比较与评价.(3), 37–42.
温忠麟, 侯杰泰, Marsh, H. W. (2003). 潜变量交互效应分析方法.(5), 593–599.
温忠麟, 侯杰泰, Marsh, H. W. (2008). 结构方程模型中调节效应的标准化估计.(6), 729–736.
温忠麟, 侯杰泰, 张雷. (2005). 调节效应与中介效应的比较和应用.,(2), 268–274.
温忠麟, 刘红云. (2020).. 北京: 教育科学出版社.
温忠麟, 刘红云, 侯杰泰. (2012).. 北京: 教育科学出版社.
温忠麟, 欧阳劲樱, 方俊燕. (2022). 潜变量交互效应标准化估计: 方法比较与选用策略.,(1), 91–107
温忠麟, 吴艳. (2010). 潜变量交互效应建模方法演变与简化.(8), 1306–1313.
温忠麟, 吴艳, 侯杰泰. (2013). 潜变量交互效应结构方程: 分布分析方法.(5), 409–414.
温忠麟, 叶宝娟. (2014). 有调节的中介模型检验方法: 竞争还是替补?,(5), 714–726.
温忠麟, 张雷, 侯杰泰. (2006). 有中介的调节变量和有调节的中介变量.,(3), 448–452.
吴冰, 王重鸣. (2010). 带有乘积项的结构方程潜变量交互模型研究.(16), 26–28.
吴艳, 温忠麟, 侯杰泰, Marsh, H. W. (2011). 无均值结构的潜变量交互效应模型的标准化估计.(10), 1219–1228.
吴艳, 温忠麟, 李碧. (2014). 潜变量交互效应模型标准化估计中的检验问题.(3), 260–264.
吴艳, 温忠麟, 林冠群. (2009). 潜变量交互效应建模:告别均值结构.(12), 1252–1259.
叶宝娟, 温忠麟. (2013). 有中介的调节模型检验方法: 甄别和整合.,(9), 1050–1060.
张莉, Wan, F, 林与川, Qiu, P. (2011). 实验研究中的调节变量和中介变量.,(1), 108–116.
郑舒方, 张沥今, 乔欣宇, 潘俊豪. (2021). 密集追踪数据分析: 模型及其应用.,(11), 1948–1969.
Aiken, L. S., & West, S. G. (1991).. Newbury Park, CA: Sage.
Asparouhov, T., & Muthén, B. (2019)..Web Notes, No. 23. Muthén & Muthén.
Asparouhov, T., & Muthén, B. (2021). Bayesian estimation of single and multilevel models with latent variable interactions.,(2), 314–328.
Baron, R. M., & Kenny, D. A. (1986). The moderator- mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations.,(6), 1173–1182.
Carden, S. W., Holtzman, N. S., & Strube, M. J. (2017). CAHOST: An excel workbook for facilitating the Johnson- Neyman technique for two-way interactions in multiple regression.,, 1–7.
Cham, H., West, S. G., Ma, Y., & Aiken, L. S. (2012). Estimating latent variable interactions with nonnormal observed data: A comparison of four approaches.(6), 840–876.
Hayes, A. F. (2018).(2nd ed.). New York: Guilford Press.
Jackman, M. G. A., Leite, W. L., & Cochrane, D. J. (2011). Estimating latent variable interactions with the unconstrained approach: A comparison of methods to form product indicators for large, unequal numbers of items.,(2), 274–288.
Kelava, A., & Nagengast, B. (2012). A Bayesian model for the estimation of latent interaction and quadratic effects when latent variables are non-normally distributed.,(5), 717–742.
Klein, A., & Moosbrugger, H. (2000). Maximum likelihood estimation of latent interaction effects with the LMS method.,(4), 457–474.
Klein, A. G., & Muthén, B. O. (2007). Quasi-maximum likelihood estimation of structural equation models with multiple interaction and quadratic effects.,(4), 647–673.
Lee, S. Y., Song, X. Y., & Tang, N. S. (2007). Bayesian methods for analyzing structural equation models with covariates, interaction, and quadratic latent variables.,(3), 404–434.
Lin, G. C., Wen, Z., Marsh, H. W., & Lin, H. S. (2010). Structural equation models of latent interactions: Clarification of orthogonalizing and double-mean-centeringstrategies.,(3), 374–391.
Liu, H., & Yuan, K.-H. (2021). New measures of effect size inmoderation analysis.(6), 680–700.
Liu, H., Yuan, K.-H., & Liu, F. (2020). A two-level moderated latent variable model with single level data.,(6), 873–893.
Liu, H., Yuan, K.-H., Wen, Z. (in press). Two-level moderated mediation models with single level data and new measures of effect sizes..
Marsh, H. W., Wen, Z., & Hau, K. -T. (2004). Structural equation models of latent interactions: Evaluation of alternative estimation strategies and indicator construction.,(3), 275–300.
McNeish, D., & Hamaker, E. L. (2020). A primer on two- level dynamic structural equation models for intensive longitudinal data in Mplus.,(5), 610–635.
Muthén, L. K., & Muthén, B. O. (1998/2017).. Muthén & Muthén.
Ozkok, O., Vaulont, M. J., Zyphur, M. J., Zhang, Z., Preacher, K. J., Koval, P., & Zheng, Y. (in press). Interaction effects in cross-lagged panel models: SEM with latent interactions applied to work-family conflict, job satisfaction, and gender..
Serang, S., Jacobucci, R., Brimhall, K. C., & Grimm, K. J. (2017). Exploratory mediation analysis via regularization.,(5), 733–744.
Wen, Z., Marsh, H. W., & Hau, K. -T. (2010). Structural equation models of latent interactions: An appropriate standardized solution and its scale-free properties.,(1), 1–22.
Wen, Z., Marsh, H. W., Hau, K.-T., Wu, Y., Liu, H., & Morin, A. J. S. (2014). Interaction effects in latent growth models: Evaluation of alternative estimation approaches.,(3), 361–374.
Wu, Y., Wen, Z., Marsh, H. W., & Hau, K. -T. (2013). A comparison of strategies for forming product indicators for unequal numbers of items in structural equation models of latent interactions.,(4), 551–567.
附录:显变量的调节效应分析的程序
注:“LOOP(z, –2.9032, 3.0354, 0.1)”表示调节变量Z的最小值和最大值是–2.9032和3.0354。在简单斜率图中, 横轴表示调节变量Z, 每隔0.1取一个点。
Methodological research on moderation effects in China’s mainland
FANG Jie1, WEN Zhonglin2, OUYANG Jinying2, CAI Baozhen2
(1Institute of New Development & Department of Applied Psychology, Guangdong University of Finance & Economics, Guangzhou 510320, China) (2School of Psychology & Center for Studies of Psychological Application, South China Normal University, Guangzhou 510631, China)
Moderation models are frequently used in the research of psychology and other social science disciplines. Moderation indicates that the strength and/or direction of the relation between an independent variable and a dependent variable is affected by a third variable called the moderator. Methodological research on moderation effects in China’s mainland covers the following topics: moderation effects of observed variables, latent variables, multi-level data and longitudinal data; the single-level moderation effect analysis based on a two-level regression model; the integration model of moderation and mediation. Finally, the future research directions are discussed.
moderating effect, latent variable, categorical variable, multilevel data, longitudinal data
2021-12-29
* 国家自然科学基金项目(32171091)、国家社会科学基金项目(17BTJ035)资助。
温忠麟, E-mail: wenzl@scnu.edu.cn
B841

