基于DOK理论二次函数深度学习的评价研究

张 冰，张玉娟

(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

教育部2016年颁布的《中国学生发展核心素养》指出：核心素养以培养“全面发展的人”为核心，学生发展核心素养指学生应具备的，能够适应终身发展和社会发展需要的必备品格和关键能力[1].深度学习是培育学生核心素养的重要路径，发展学生的核心素养就应使学生进行深度学习[2].在当前的数学学习中，迫于中考升学的压力，大多数初中生为了提高成绩，往往机械地死记硬背一些公式、法则等知识点，未能真正理解知识的本质，没有将知识进行深层次的剖析，没有深入思考知识之间的联系，不能灵活地拓展和运用所学知识，学习仅停留在浅层阶段.深度学习是重视理解知识本质、强调新旧知识之间联系、把知识拓展到实际应用中、能进行自我反思并形成批判性高阶思维的学习.由此可见，初中学生进行数学深度学习非常必要.

在教育领域中，深度学习日益受到关注.深度学习最早是由美国学者FERENCE和ROGER[3]在1976年提出.1995年HALE等[4]提出“高阶思维”的观点，将深度学习与“高阶思维”相联系.在国内，何玲和黎加厚[5]于2005年最早提出深度学习的概念.张浩和吴秀娟[6]通过对深度学习概念的分析，提出了深度学习的特征.进入21世纪后，随着中国课程改革的不断发展以及新时期培养学生核心素养要求的提出，对学科的深度学习研究逐渐增多.不少学者对数学的深度学习进行了研究，张玉娟和王雪梅[7]基于DELC教学模式对初中数学深度学习实施路径进行了探究；程明喜[8]对促进小学数学深度学习的教学策略进行了研究.目前，关于初中数学深度学习的评价研究较少，通过对初中生数学深度学习情况进行评价，能够了解学生数学深度学习的水平，为数学教师教学提供参考.因此，有必要对初中数学深度学习评价进行研究.

二次函数是初中数学学习的重要内容，它既是一次函数的拓展，又是高中阶段二次函数内容的基础，在整个函数学习中起着承上启下的作用.二次函数在初中数学学习中既是重点也是难点，加之许多实际问题可以归结为二次函数加以研究，因此，有必要对二次函数的深度学习进行研究.

本文基于DOK(Death of Knowladge)理论，对初中生二次函数深度学习的整体水平进行评价研究，并探究不同类型学校学生二次函数深度学习的水平.

1 理论基础

1.1 深度学习

对于深度学习的理解，学者安富海[9]认为，深度学习是一种基于理解的学习，是指学习者以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新的知识和思想，并将它们融入原有的认知结构中，且能将已有的知识迁移到新的情境中的一种学习.

1.2 初中数学深度学习

初中数学深度学习是指在数学学习过程中，在教师的引导下，学生围绕具有挑战性的数学学习主题，全身心积极参与、体验成功的数学学习过程[10].在这个过程中，学习者在教师的引导下，在理解数学学科知识的基础上，能够运用策略性思维对新旧知识进行加工和反思，进行拓展性思考，具备复杂的逻辑推理能力，进而使用分析、综合等高级思考模式解决实际问题.

1.3 DOK理论

DOK理论是美国学者韦伯提出的关于知识深度水平的评价理论[11].该理论将知识深度划分为4个水平，分别是：DOK1 回忆/重现(Recall/Reproduction)，DOK2 技能/概念(Skill/Concept)，DOK3策略思维(Strategic Thinking)，DOK4 拓展思维(Extended Thinking).前两个水平是浅层学习，后两个水平是深度学习.基于DOK理论的二次函数深度学习水平评价标准如表1所示.

表1 DOK理论下二次函数深度学习水平评价标准

2 研究方法

2.1 研究对象

本研究选择A市不同类型的3所学校的初三年级学生作为测试卷发放对象，第一类是城市中心地区中学，第二类是城市一般地区中学，第三类是乡镇中学.依据学生初二年级期末考试成绩，在3所学校中各随机选择3个班级进行测试.第一类中学选取132人发放测试卷，试卷有效回收率为98.4%；第二类中学选取132人发放测试卷，试卷有效回收率为96.9%；第三类中学选取131人发放测试卷，试卷有效回收率为94.6%.共发放测试卷395份，收回有效测试卷382份，试卷有效回收率为96.7%.

2.2 测试卷设计

本测试卷以韦伯的DOK理论为基础，并参照《义务教育数学课程标准》中对于二次函数的内容要求进行编制.为考查学生二次函数的深度学习水平，共编制9道题，其中选择题4道、填空题2道、解答题3道.

第4题、第5题以及第8题(1)测试目标水平为DOK2，旨在考查学生对二次函数三种解析式之间的转化、根据二次函数的表达式推断二次函数的图像,以及根据二次函数与一元二次方程的关系进行方程与函数的转化进而求解一元二次方程的根的能力.例如:二次函数y=x2+2x+1与坐标轴交点坐标是( ).

第6题、第8题(2)以及第9题(1)测试目标水平为DOK3，旨在考查学生建立二次函数、应用二次函数概念及图像解决实际问题的能力.例如:函数y=(m-3)xm2+2m-13+mx是二次函数，则m的值是( ).

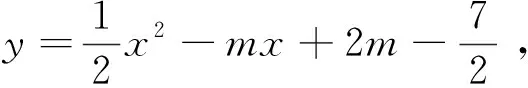
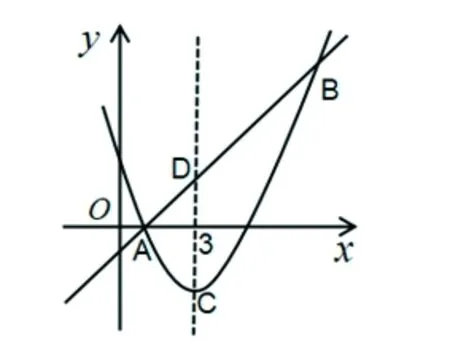
图1 抛物线

2.3 测试卷分数

根据二次函数深度学习水平的划分给出评分依据，如表2所示.再根据测试卷的设计和评分依据得到二次函数深度学习测试卷各题分数表，如表3所示.本测试卷满分58分.

表2 测试卷评分依据

表3 测试卷各题分数表

2.4 测试卷各水平之间的相关性

由表4可得，组内两两水平相关,达到0.05的显著性水平,相关系数在0.168～0.792之间，为正相关.4个层次与总测试卷之间相关系数在0.549～0.823之间，表明各水平与整个测试卷一致，是正相关.

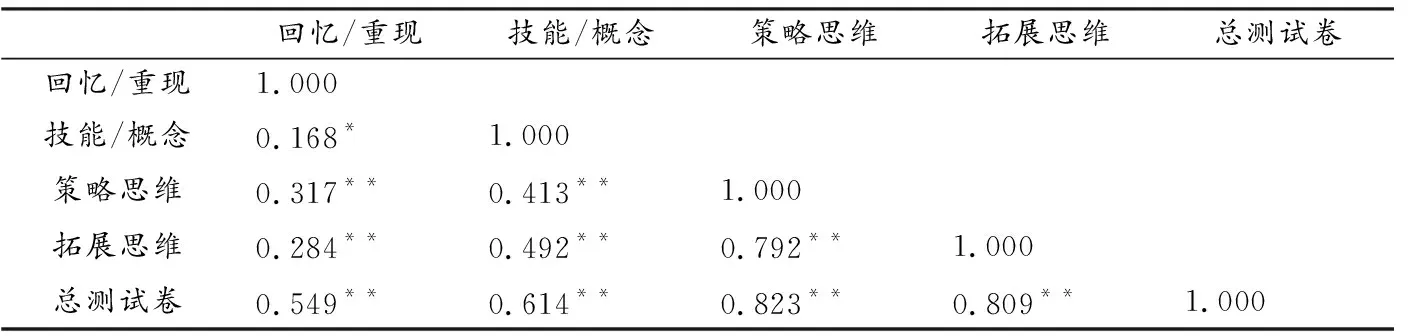
表4 各水平间相关系数矩阵

2.5 测试卷的信效度

运用SPSS 22.0对测试卷进行信效度检验，结果如表5和表6所示.

表5 可靠性统计量

由表5可知，测试卷的信度系数为0.848，处于0.75～0.9之间，说明此测试卷信度较好；由表6可知，测试卷效度系数是0.859，大于0.5，说明此测试卷效度良好.

表6 KMO和巴特利特检验

3 二次函数深度学习的调查与分析

3.1 学生二次函数深度学习水平整体分析

由表7可以看出，学生二次函数4个知识深度水平得分率相差较大，DOK1和DOK2得分率较高，分别为83.97%和82.24%，说明绝大多数学生二次函数学习达到了技能/概念水平，处于浅层学习；DOK3得分率为68.14%，说明多数学生达到了策略思维水平，超过三分之二的学生对于二次函数进行了深度学习；DOK4得分率最低，为35.56%，说明少数学生达到拓展思维水平.

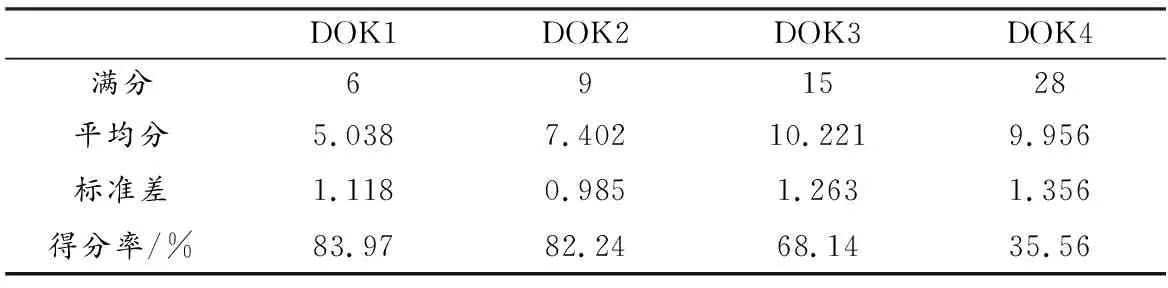
表7 学生二次函数深度学习的整体水平

3.2 不同类型学校学生二次函数深度学习水平差异分析

为研究不同类型学校学生二次函数深度学习水平的差异，用SPSS 22.0进行t检验分析，结果如表8所示.由表8可以看出，不同类型学校学生在DOK1和DOK2上没有显著性差异，而在DOK3和DOK4上存在显著性差异，说明3类学校学生在二次函数深度学习上存在显著性差异.

表8 不同类型学校学生二次函数深度学习独立样本t检验

由表9可知，第一类学校、第二类学校和第三类学校DOK3得分率分别为79.74%、65.84%和48.25%，说明对于二次函数，第一类学校绝大多数学生能够进行深度学习，第二类学校多数学生能够进行深度学习，第三类学校少数学生能够进行深度学习.通过对DOK3和DOK4得分率分析，对于二次函数深度学习，第一类学校最好，第二类学校次之，第三类学校最差.

表9 不同类型学校学生深度学习得分率

4 研究结论

4.1 初三学生二次函数深度学习水平有待提高

通过对学生二次函数深度学习水平进行整体分析，得到策略思维水平得分率为68.14%，这表明，学生二次函数深度学习整体水平一般，还有少数同学二次函数深度学习水平有待提高.学生对二次函数的概念、公式和法则等能够较好地记忆，但是，在对二次函数进行策略性和拓展性思考、使用综合与反思等高阶思维解决现实问题时存在较多困难.

4.1.1 二次函数概念理解不深刻 在二次函数概念的实际应用题解析中存在审题不清、找不到等量关系等问题.测试卷第6题考查学生对二次函数概念的掌握情况：首先，根据二次项次数为2列出一元二次方程；其次，求解参数；最后，根据二次项系数不为0，把不符合题意的结果舍去.测试结果显示，多数学生没有答对，部分学生给出两个答案，但没有将不合题意的解舍去.研究发现，出现这种问题的原因是学生对二次函数概念的理解不深入，对二次函数概念死记硬背.

4.1.2 二次函数性质应用不灵活 在二次函数解题过程中经常会用到二次函数的性质，测试卷第7题(2)和第8题(3)考查学生应用二次函数图像的性质求最值问题的能力.对于实际问题，首先，要建立二次函数模型；其次，应用二次函数图像的性质讨论二次函数的增减性；最后，利用顶点坐标公式计算最值.通过测试卷的答题情况可以看出，一些学生答题出现空白情况，一些学生只给出二次函数解析式，还有一些学生最值计算错误.研究发现，出现这种问题的原因是不能灵活应用二次函数图像的性质讨论增减性，不能灵活应用顶点坐标公式计算最值.

4.1.3 数学思想方法掌握不牢固 数学思想方法的掌握在二次函数的学习中是非常重要的，数形结合、分类讨论、转化与化归是解答二次函数问题经常使用的数学思想方法.测试卷第9题(1)考查学生将二次函数图像与x轴交点问题转化成一元二次方程根问题的能力.首先，利用二次函数与一元二次方程的关系写出一元二次方程；其次，求出一元二次方程的判别式；最后，证明判别式恒大于零.由实际答题情况看，部分学生出现卷面空白的情况.通过对这部分学生的访谈发现，原因在于学生没有把未知问题转化为已知问题进行求解.测试卷第9题(2)考查学生数形结合思想方法的掌握情况.首先，利用对称轴公式求出二次函数解析式中的参数；其次，求出抛物线、直线和对称轴的三个交点坐标；最后，利用平移证得所求四边形是正方形.多数学生能够求出交点坐标，但是不知道利用平移证明所求四边形为正方形，这说明学生不能利用代数方法求解几何问题，没有很好地掌握数形结合的思想方法.

4.2 学生知识基础影响学生二次函数深度学习水平

通过对不同类型学校学生二次函数深度学习进行差异分析得到：在策略思维水平上，第一类学校得分率为79.74%，第二类学校得分率为65.84%，第三类学校得分率为48.25%.结果表明，不同类型学校学生二次函数深度学习水平存在显著性差异，且城市中心地区中学高于城市一般地区中学，城市一般地区中学高于乡镇中学.

二次函数深度学习水平的高低受到与二次函数相关知识掌握情况的影响：一次函数的知识迁移到二次函数的学习中，能加深学生对二次函数概念和图像性质的理解；多项式和一元二次方程等相关知识的掌握程度直接影响学生二次函数深度学习水平的达成.二次函数与其他数学知识的横向联系，拓宽了学生的学习范围，给学生二次函数深度学习带来困难.二次函数经常和一次函数、几何图形相结合，利用数形结合进行综合、分析、反思等高阶思维来解决复杂问题.应用二次函数能够分析和解决一些实际问题，不同领域的知识如果不能准确地掌握，就不能建立正确的二次函数数学模型，实际问题就得不到解决.可见，不同类型学校学生知识基础的差异导致他们二次函数深度学习水平存在显著性差异.