含阻尼效应的黏弹性杆稳态响应的解析解1)

陈 波 李映辉 李翔宇 袁江宏

(西南交通大学力学与航空航天学院，成都 610031)

杆件在工程结构中广泛应用，如桁架[1]、桩基[2]和机床滚珠丝杠[3-4]。其动力行为分析对这些结构的优化设计、健康监测和振动控制起着重要作用，研究备受关注。Kumar等[5]研究了截面积按多项式或正弦函数变化的变截面杆的自由振动，给出了固有频率的精确解。Erol等[6]处理了由黏弹性层连接的双杆系统的强迫振动问题。邢沁妍等[7]用伽辽金有限元能量投影法，分析了黏性阻尼下变截面杆的轴向受迫振动。借助振型分解和杜哈梅积分，范学明等[8]导出了杆强迫振动的基本解。黏弹性杆在频域内的振动控制方程为二阶复系数微分方程，与弹性杆相比，其模态特性信息（频率和模态函数）较难获取。李会侠等[9]用复数理论，研究了固定–自由黏弹性杆的振动特性。张菊梅[10]提出小波–微分求积法，得到了黏弹性杆自由振动和强迫振动的数值解。Shatalov等[11]基于伽辽金法，给出了固定–自由黏弹性杆的强迫振动响应。Gera等[12]求解了轴向匀速运动的纵向非均匀黏弹性杆的强迫振动。

以上文献对任意边界条件下黏弹性杆振动解析研究有限，因此本文将各种边界条件表示为统一形式，基于格林函数法和叠加原理导出简谐激励和黏性阻尼下，任意边界条件开尔文黏弹性杆稳态响应的解析解。

1 控制方程及其解

受轴向力q(x,t)的开尔文黏弹性杆，其长度为L，弹性模量为E，横截面积为A，密度为ρ，开尔文黏性阻尼系数为ηm，外部阻尼系数为ηe。轴向位移为u，则杆纵向振动方程为[9]

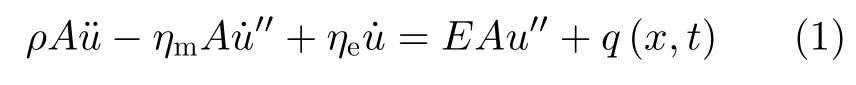
式中 “′”和“·” 分别表示对x和t求导。设q(x,t) =Q(x)eiΩt，式中i为虚数单位，Ω为外载荷圆频率。则u(x,t) =U(x)eiΩt。式（1）可表示为

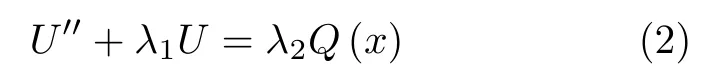
λ1和 λ2定义为

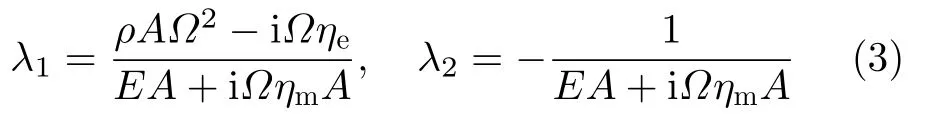
由叠加原理，式（2）的解可写成

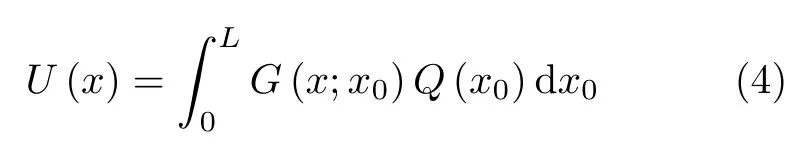
其中G(x;x0) 为杆稳态响应的格林函数，其物理含义为：x=x0处单位载荷作用下在x处所产生的位移。它是式(5)微分方程的解

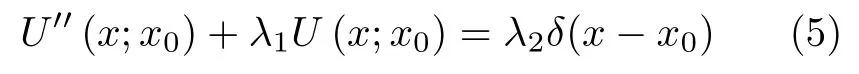
式中δ(·) 为狄拉克函数。由式（5），有G(x;x0) =U(x;x0) 。式（5）对x进行拉普拉斯变换得

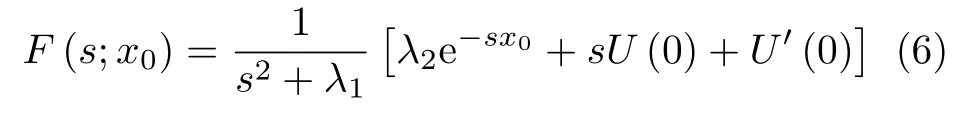
式中F(s;x0) 表示U(x;x0)的拉普拉斯变换，U(0) =U(0 ;x0) 和U'(0)=U'( 0 ;x0) 是由边界条件确定的待定常数。对式（6）进行拉普拉斯逆变换得

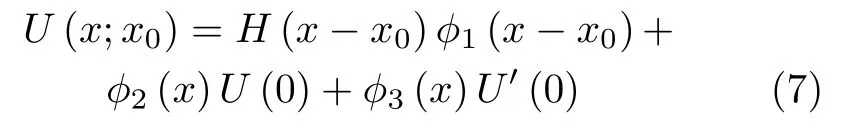
式中H(·)为单位阶跃函数，及

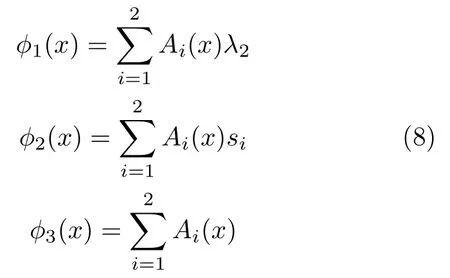
其中

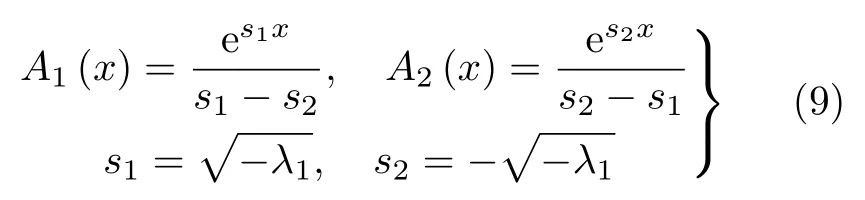
将x=L代入式（7）及其一阶导数得到

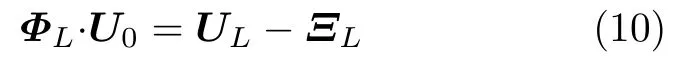
式中

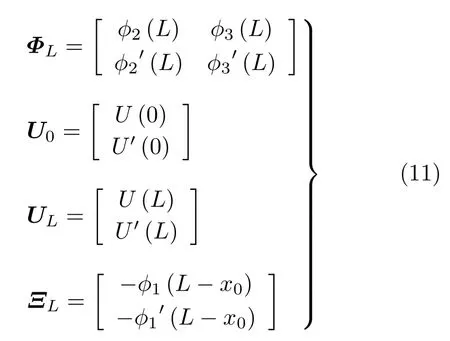
式中U(L) =U(L;x0) ，U'(L) =U'(L;x0) 。杆的各种边界条件可统一表示为

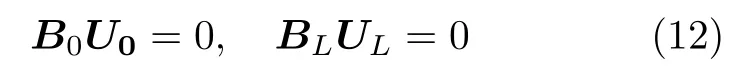
式中B0和BL是由边界条件决定的常数矩阵。如两端固定的杆，x= 0和L处的位移为0，有B0=BL= [1 0]。其他边界条件的B0和BL见表1。联合式（10）和（12）得

表1 不同边界条件的系数矩阵B0 和BLTable 1 Coefficient matrixes B0 and BL for various boundary conditions

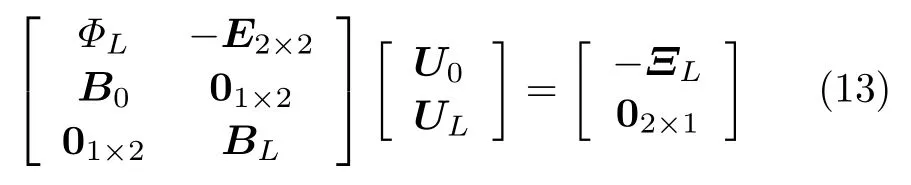
式中E代表单位矩阵，0代表零矩阵。由式（13）可求得U0，将其代入（7）可得杆稳态响应的格林函数。不考虑外激励，杆的固有频率可通过令式（13）系数矩阵行列式为0求得，此时Ω对应系统的固有频率。

由式（7）得到杆的格林函数解G(x;x0) 后，借助式（4）可得外激励Q(x)作用下的稳态响应U(x)。注意在材料黏性阻尼系数ηm≠ 0和外部阻尼系数ηe≠ 0情况下，式（3）中的系数λ1和λ2均为复数，意味着U(x)为复数函数，即U(x) = α(x)+iβ(x)，其中 α(x)和β(x)是关于x的实数函数。分两种情况讨论：

（1）若q(x,t) =Q(x)cos (Ωt), 有

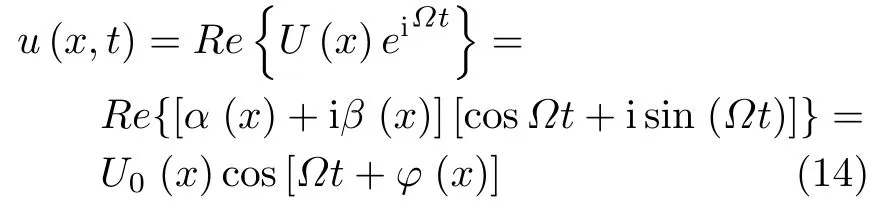
（2）若q(x,t) =Q(x)sin (Ωt), 有

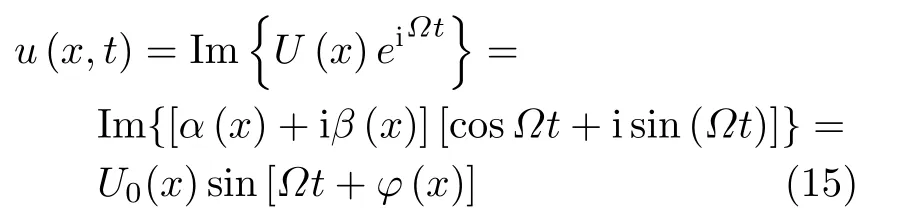
式（14）和式（15）中

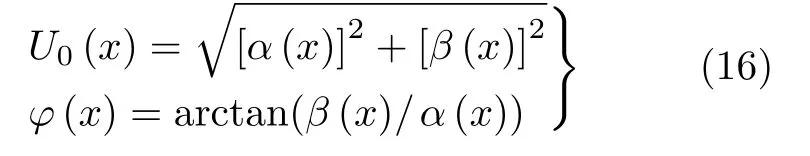
由式（14）～式（16）可见

（1）式（14）或式（16）中φ(x) 的物理意义为杆x处的响应与外激励之间的相位差。

（2）当阻尼系数ηm= 0和ηe= 0时，相位差φ(x) = 0。由式（14）或式（15），杆的位移在时间和空间上可分离，即可写成u(x,t) =U0(x)·cos (Ωt)或U0(x)sin (Ωt)形式。 此时U0(x)不仅反映了杆的位移幅值，还反映其振动形状，cos (Ωt)或sin (Ωt) 相当于结构位移的尺度因子。因此不考虑阻尼时U0(x)足以展现其动力学行为。

（3）当阻尼系数 ηm≠ 0 或 ηe≠ 0 时，U0(x) 仅反映结构的位移幅值。杆上任意两点x=x1和x=x2处的位移不同步，存在相位差|φ(x1)-φ(x2)|，此时阻尼杆的位移在时空上不可分离，即不能写成u(x,t) =U0(x)p(t)（p(t)为时间t的实数函数）形式。因此必须用杆的动态位移u(x,t) 展现其动力学行为。

2 验证和讨论

考虑L= 1 m，E= 2×1011N/m2， ρ =7 850 kg/m3，A= 2.5×10–3m4，q(x,t) =Q(x)cos (Ωt)（Q(x) = 10 N/m），边界条件为固支–自由杆。引入无量纲量

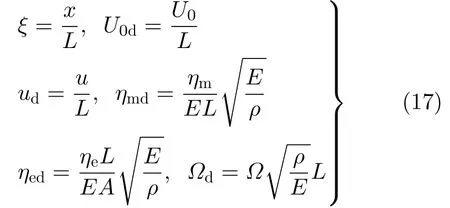
为检验本文方法，图1给出了ηm= ηe= 0时，x=L处的幅频响应曲线。其中无阻尼（ηm=ηe= 0）下固支–自由杆的固有频率精确解已在振动力学教材给出，其第n阶固有频率为 (2n–1)·π(E/ρ)0.5/(2L)。可见激发共振峰的外激励频率与固有频率完全一致。

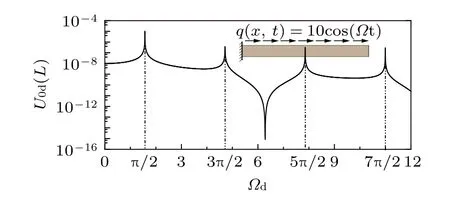
图1 固定–自由杆x = L处的幅频响应曲线Fig.1 Amplitude-frequency response curve of a fixed-free rod at x = L

为了验证先前的讨论，图2给出了不同材料黏性系数ηmd和位置ξ下固定–自由杆的时间历程曲线。由图2(a)可见，不同黏性系数ηmd下，杆的时间历程曲线并不同步，与理论预期一致，表明阻尼的存在导致结构振动和外激励作用在时间上是异步的，存在相位差。另外，由图2(b)可知阻尼的存在导致杆上各点振动异步，存在相位差，从而验证了前述阻尼作用下杆位移在时间和空间上不可分离的结论。

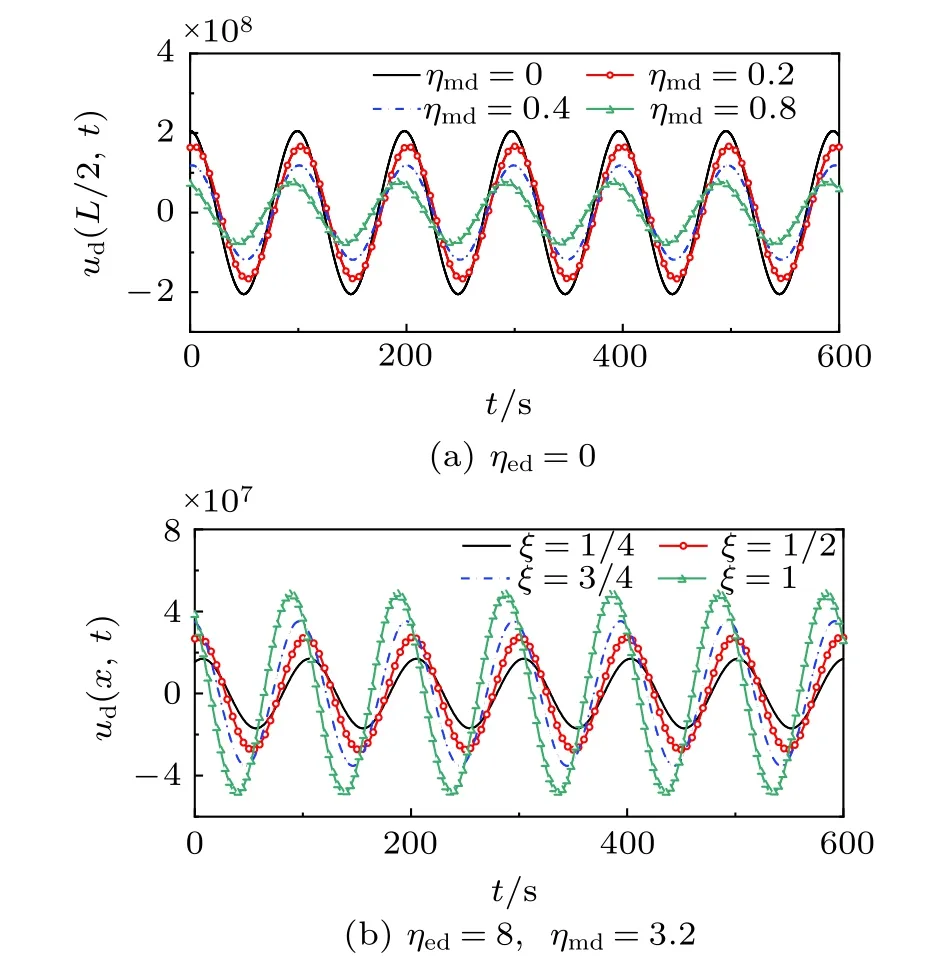
图2 不同材料黏性系数ηmd和位置ξ下固定–自由杆的时间历程曲线（Ωd = 0.4 π ）Fig.2 Dynamic deflection of the fixed-free rod versus time under different viscous coefficients of the material and locations (Ωd = 0.4 π )

3 结论

本文用格林函数法结合叠加原理，得到了任意边界下考虑外部阻尼的黏弹性杆在简谐激励作用下稳态响应解析解。将各种边界条件统一为矩阵形式，提高了编程和计算效率。理论和数值结果均揭示了阻尼作用下杆的位移在时间和空间上是不可分离的。本文方法不仅适用于黏弹性杆纵向振动，还可应用于其他一维连续系统，如欧拉–伯努利梁和铁木辛柯梁横向振动，欧拉–伯努利梁双向振动，还可扩展到复杂结构，如阻尼作用下铁木辛柯梁弯扭耦合振动[13]和黏弹性层连接双梁系统的耦合振动[14]。