塑性力学教学中Mises屈服准则几何轨迹证明1)
梅瑞斌 包 立 刘相华 *
*(东北大学材料与科学工程学院,沈阳 110819)
†(东北大学秦皇岛分校,河北秦皇岛 066004)
屈服准则最早起源于岩土、岩石研究,常见的有用于金属塑性屈服的米塞斯(Mises)、屈雷斯加(Tresca)准则以及用于岩土力学分析的德鲁克–普拉格(Drucker–Prager)、莫尔–库仑(Mohr–Coulomb)、辛凯维奇–潘德(Zienkiewicz–Pande)等准则,而金属塑性力学中主要介绍Mises屈服准则和Tresca屈服准则物理意义、数学表达式异同以及几何轨迹关系。作为塑性力学的基础理论,屈服准则在力学分析和参数优化中占据着重要地位[1-4],也是各高校金属塑性成形力学[5]、塑性加工力学基础[6]、塑性力学基础[7]、弹塑性力学[8]等塑性力学类课程以及金属塑性成形原理[9]、材料成形原理[10]等塑性原理类相关课程中重点讲授的知识点。目前教材中关于几何轨迹解释和证明较为简略,导致课程讲授中学生对屈服准则的几何轨迹理解不深刻、不透彻。为此,本文从学生理解角度对屈服准则几何轨迹进行了梳理和证明,根据多年教学实践效果表明该方法对学生加深屈服准则知识点理解有较大帮助。
1 平面应力条件下屈服准则轨迹证明
Tresca屈服准则是1864年法国工程师Tresca提出的最大剪应力准则,即:对同一金属在同样的变形条件下,无论是简单应力状态还是复杂应力状态,只要最大剪应力达到某一极值就发生屈服,然后分别引入拉伸屈服强度σs和剪切屈服强度k后,该准则可以描述为
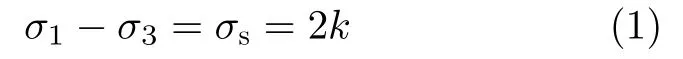
1913年,Mises从数学角度推导了Mises屈服准则表达式,1924年,汉基证明了该表达式为能量准则,即:对各向同性材料来说,当变形体内部所积累的单位体积弹性变形能达到一定值时,材料发生屈服且该变形能只与材料性质有关,而与应力状态无关。引入拉伸屈服强度σs和剪切屈服强度k后,该准则可以描述为
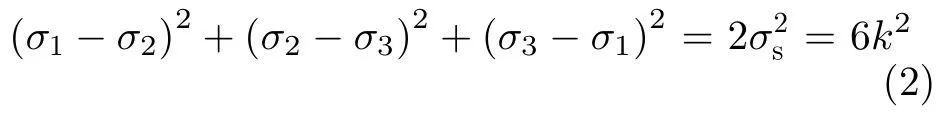
对于Mises屈服准则来说,假定在主应力坐标系下,σ3=0 ,将其代入准则表达式可以得到
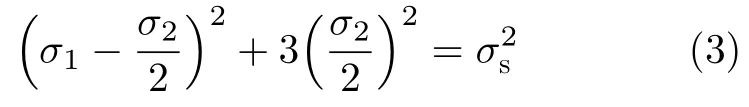
令σ1-σ2/2=x,σ2/2=y,则式 (3)变为
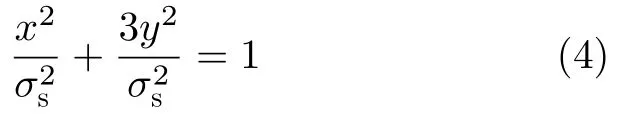
式(4)所示的几何图形为标准椭圆,长半轴为σs,短半轴为。又由假设σ1=x+y,σ2=2y,可得Mises屈服准则平面条件下σ1和σ2在σ3=0平面内是椭圆,与标准椭圆相比,轴向旋转45°(图1(a)所示),旋转后长半轴变为,短半轴变为。对于Tresca屈服准则来说,假定σs>0 ,σ3=0 ,则可以得到Tresca屈服准则为Mises准则的内接六边形(图1(b)所示)。
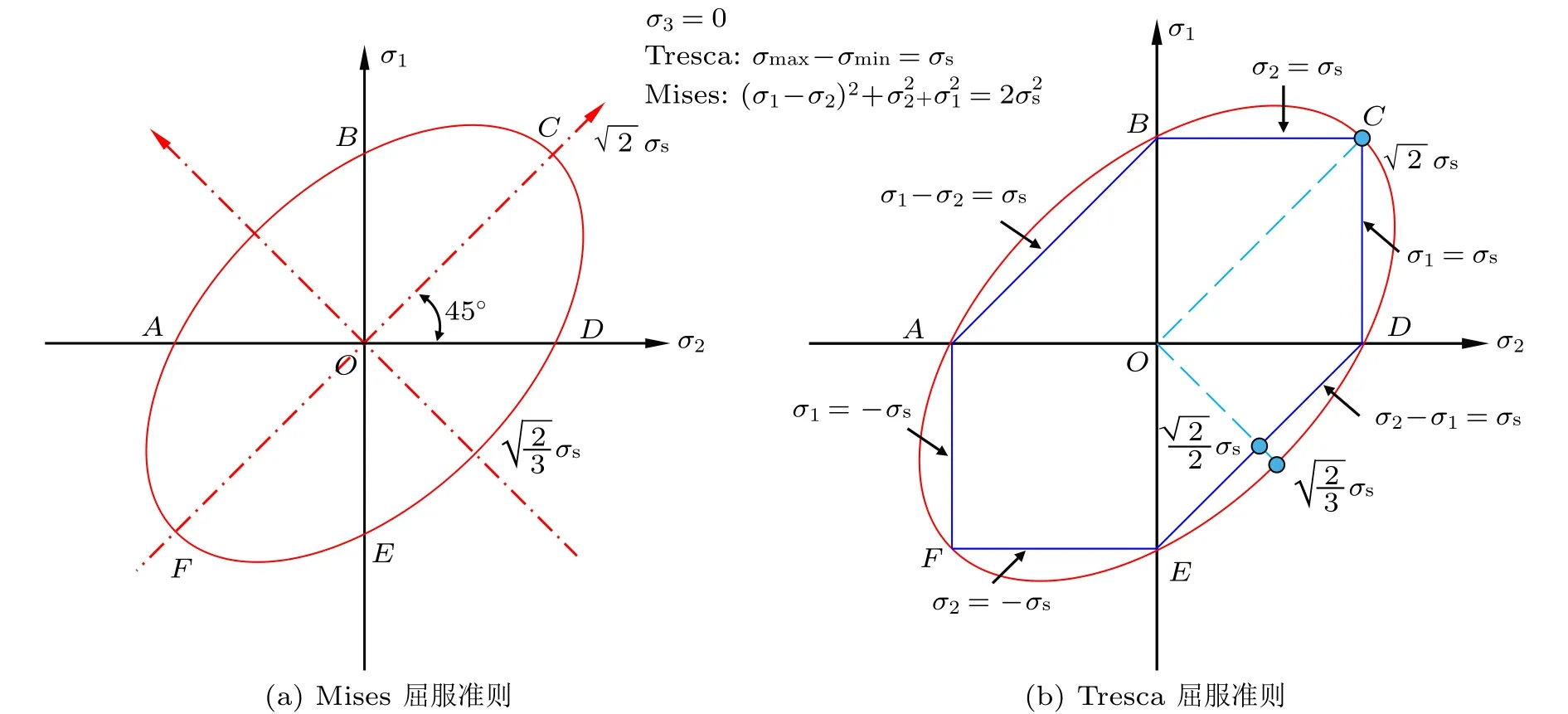
图1 平面应力下屈服准则的几何图形
在平面应力条件下Mises屈服准则几何轨迹是椭圆,为进一步分析,从平面直角坐标系出发,对该椭圆方程进行证明。
证明:假设坐标系O-XY和坐标系O'-X'Y'的关系如图2所示。
对于图2所示坐标系,进行如下描述:坐标系O-XY逆时针旋转θ后与坐标系O'-X'Y'重合,或者表述为坐标系O'-X'Y'顺时针旋转θ后与坐标系O-XY重合,利用数学上的坐标变换相关知识可以得到
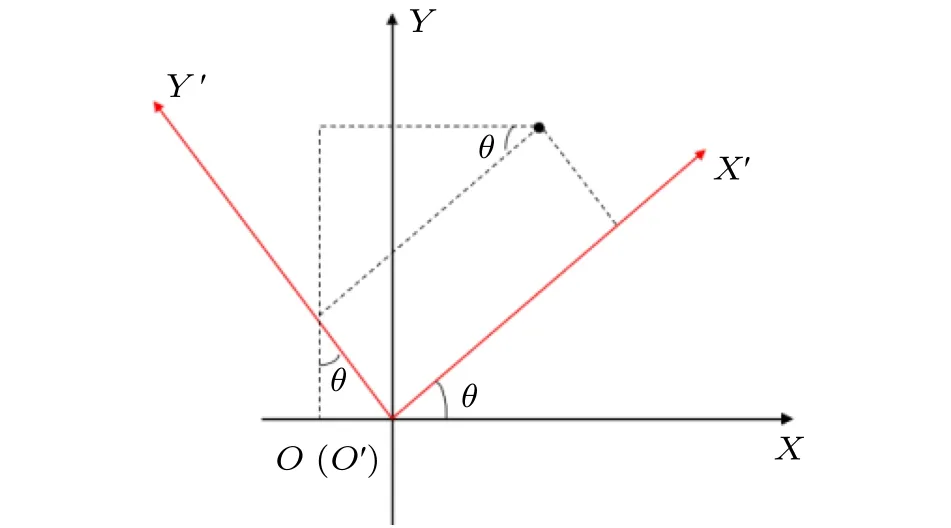
图2 旋转矩阵与坐标系变换
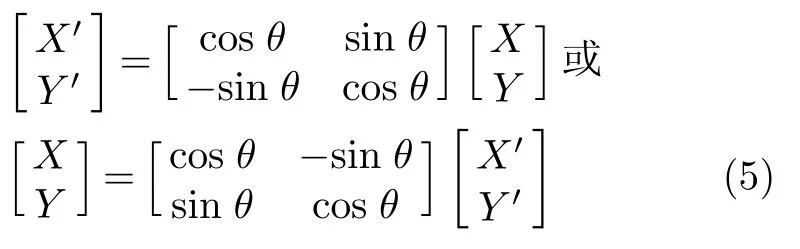
对于Mises屈服准则的几何变换,坐标变换关系表述为
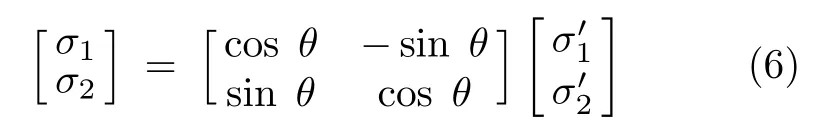
由式(6)可得新旧坐标系下应力关系表达式为
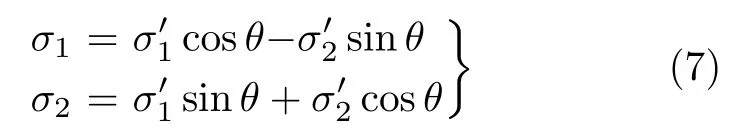
将式(7)代入到平面应力条件下的Mises屈服准则表达式(2)中,可得
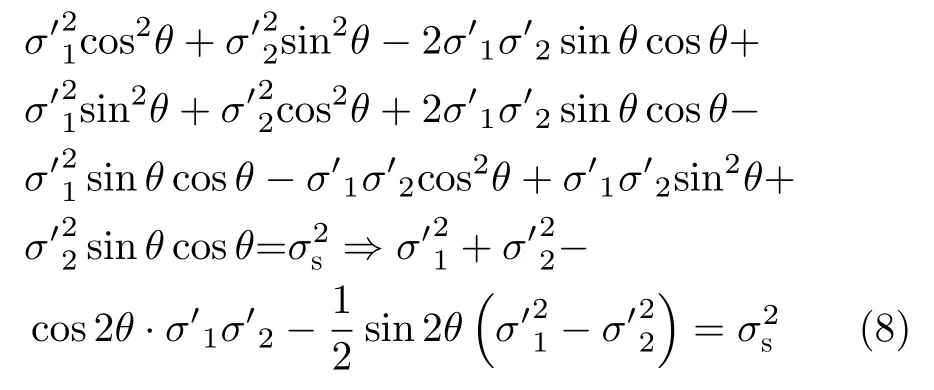
令 c o s(2θ)=0 , s i n(2θ)=1 ,即θ=,可得到
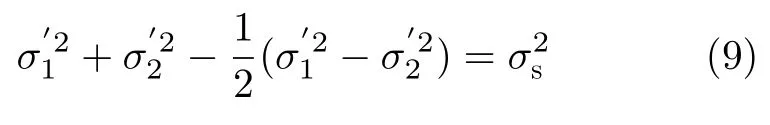
将式(9)进行标准化处理后得到
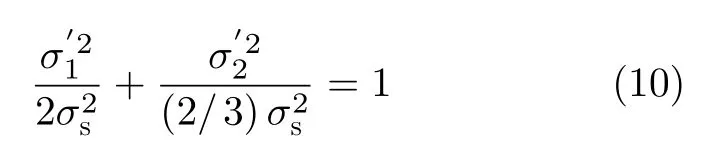
式(10)为标准的椭圆方程,根据矩阵变换条件可知,平面应力状态的下Mises屈服准则是由标准椭圆逆时针旋转45°得到,其长半轴及短半轴长度分别为和。
所以,图1中所示六边形ABCDEF为Tresca屈服准则几何轨迹,外接椭圆轨迹为Mises屈服准则几何轨迹。
2 空间米塞斯屈服准则几何证明
Mises屈服准则平面几何轨迹为椭圆,故在空间中只有椭圆面和圆柱面两种可能。假设一点P的应力状态(σ1,σ2,σ3)可用向量OP来表示,如图3所示。
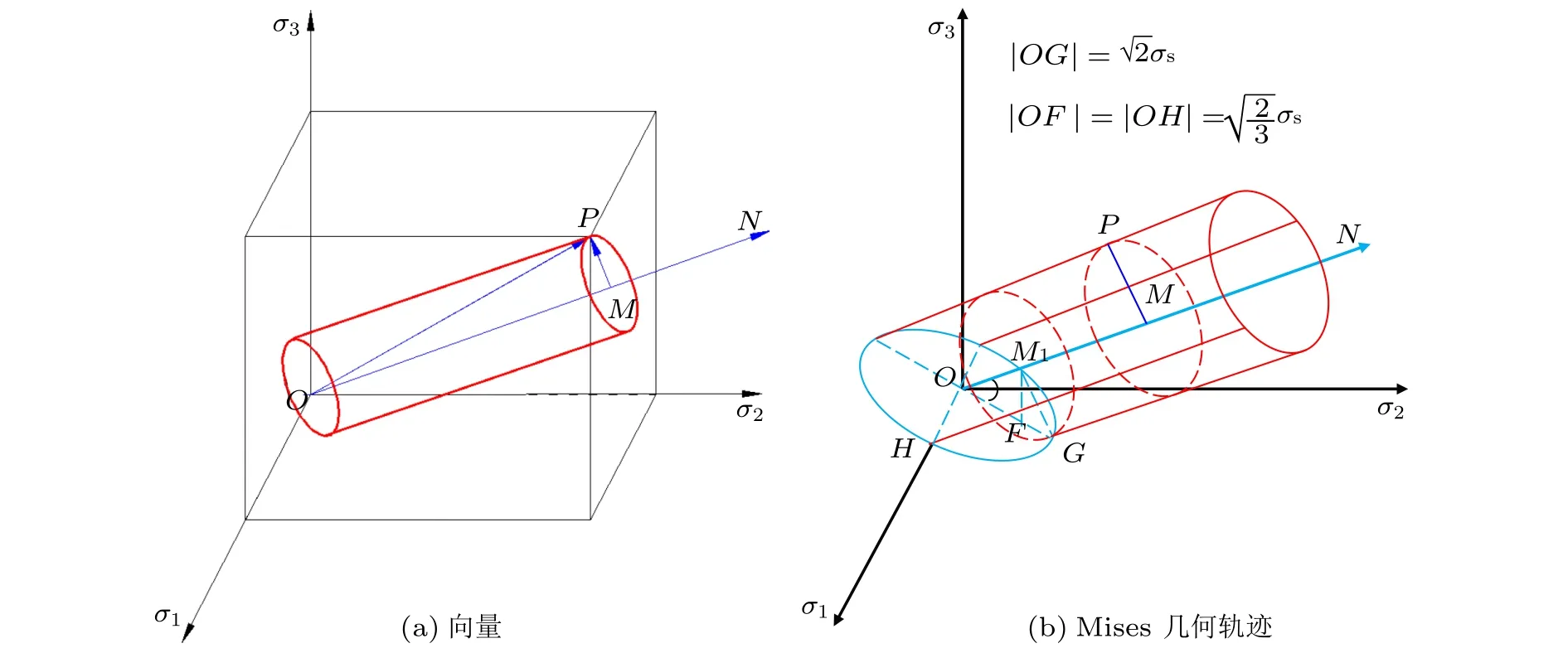
图3 向量 O P 及几何图形示意图
过坐标原点O作与坐标轴成等倾角的直线ON,向量OP在该直线上的投影为OM,由此,向量OP可分解为向量OM与MP且有
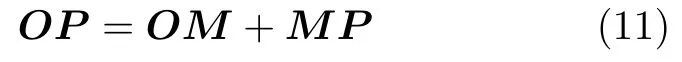
由图3很容易得到OP线段的模为|OP|2=所以MP线段的模为
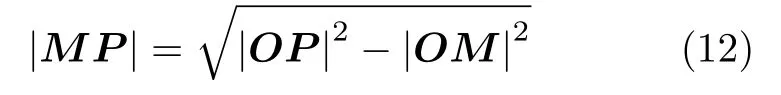
为求得OM的模,令M点的坐标为x,y和z,OP矢量为(x,y,z),根据矢量关系,MP矢量为(x-σ1,y-σ2,z-σ3),由于OM⊥MP,所以
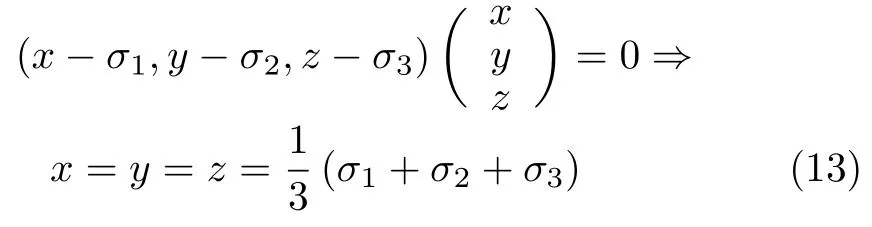
故,矢量OM的模为
将OP和OM向量的模代入式(12)后,可得矢量MP的模为
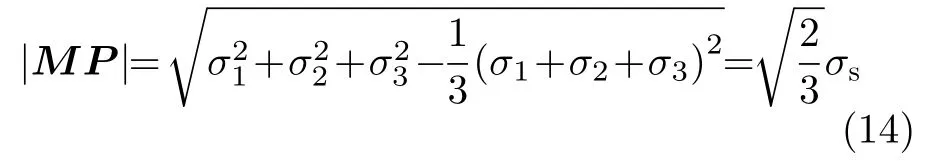
由式(14)可以看出,以OM为轴心,MP为半径,旋转形成一个圆柱面,其该圆柱面的半径与平面应力条件下Mises屈服准则椭圆的短半轴相等。如果能证明该圆柱面与σ3=0 平面的交线和式(10)表示的椭圆的长半轴相等,则可推出该圆柱面即为Mises屈服准则的空间几何轨迹。
证明:由图3可知,OM与三个坐标轴成等倾角,方向余弦为,过M点作σ1和σ2组成的平面的垂线,交点为F,连接OF并延伸至G。
根据M点和F点坐标能够得到线段OF的长度为,于是
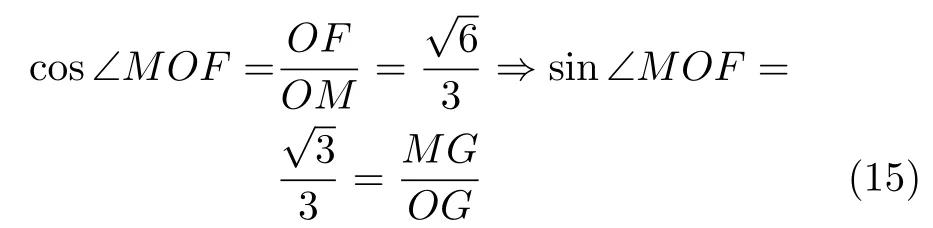
将MG长度代入式(15)可得到线段OG长度为,正好等于平面应力条件下椭圆长半轴的值。所以该空间圆柱面与σ3=0 平面相交曲线是长半轴为,短半轴为的椭圆几何轨迹。
由此得证,Mises屈服准则的空间图形是以直线ON为轴线,以为半径的圆柱面,该圆柱面轴心线方向与三个主坐标轴夹角相同。根据Mises屈服准则和Tresca屈服准则平面关系可以证明Tresca屈服准则的空间图形为正六棱柱面。
3 Tresca与Mises几何轨迹关系
由前述可知,用拉伸屈服应力σs描述的Mises屈服准则空间轨迹为圆柱面,而Tresca屈服准则为内接正六边形,如图1(b)所示。在引入罗德系数条件下,Mises屈服准则可以简化为
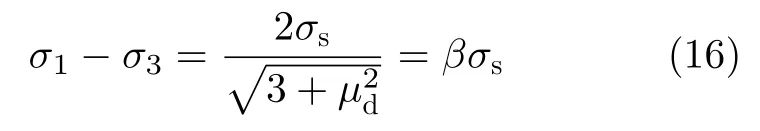
其中,μd为罗德系数,β为简化系数。
一般根据式(16)可知:(1)轴对称应力状态下,β=1 ,两个屈服准则表达形式相同;(2)平面应变或纯剪应力状态下,,两个准则差别最大。
实际上,当屈服准则用剪切屈服强度k描述时,由于Mises屈服准则下故式(16)表示的Mises屈服准则简化形式描述为
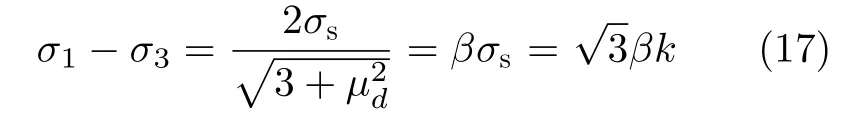
根据式(17)可知:(1)轴对称应力状态下,β=1时,Mises屈服准则,而Tresca屈服准则σ1-σ3=2k,两个准则形式并不相等;(2)平面应变或纯剪应力状态下,时,Mises屈服准则σ1-σ3=2k,和Tresca屈服准则表达形式相同。
综上所述,不难得到当用剪切屈服强度描述屈服准则时,Mises屈服准则和Tresca屈服准则表达式形式与采用拉伸屈服强度描述时正好相反。如果用σs描述屈服准则,Tresca内接于Mises屈服准则几何轨迹,而如果用k来描述,则平面应力条件下的屈服准则几何轨迹如图4所示,此时,Tresca屈服准则仍然为六边形,Mises屈服准则为椭圆,椭圆内接于六边形,空间图形也是如此。
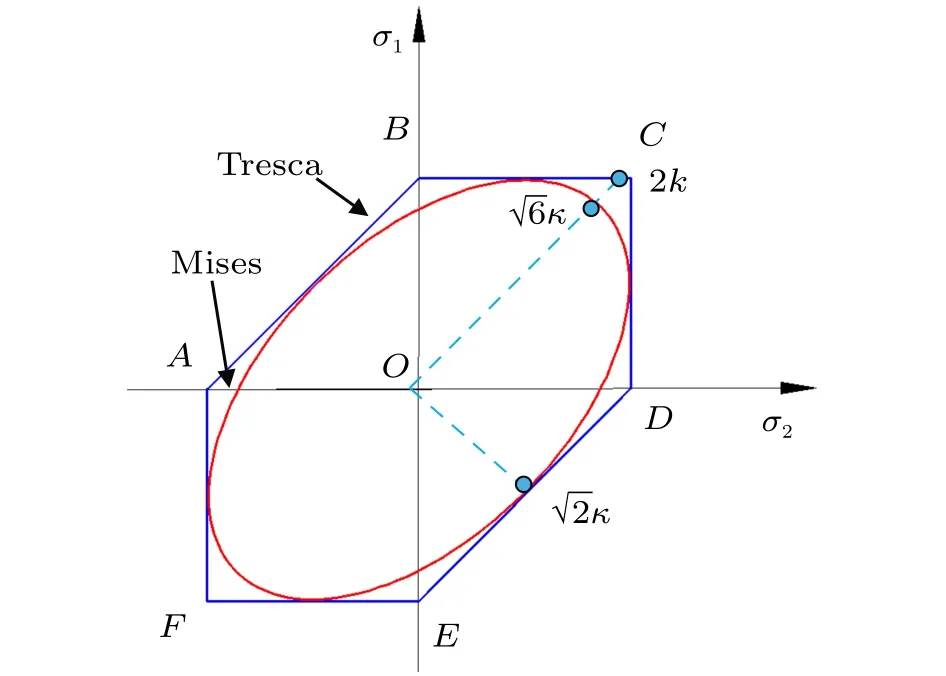
图4 剪应力常数描述时平面应力条件的屈服准则几何轨迹
4 结论
针对塑性力学教学和应用中的重点知识,从教学和学生学习角度利用坐标变换和几何关系推导证明了Mises和Tresca屈服准则的几何轨迹,讨论了两个准则表达式以及几何轨迹的关联性和本质区别。平面应力条件下Mises和Tresca为椭圆和六边形,空间图形为圆柱面和正六棱柱面,当准则用屈服应力σs表示时,Tresca几何轨迹内接于Mises几何轨迹,当用剪切屈服强度k表示时,Tresca几何轨迹外接于Mises几何轨迹。
——对2018年广州市一道中考题的研究

