“信号与系统”课程思政教学案例的探索与实践

李艳凤 陈后金 彭亚辉 陶 丹 李居朋

(北京交通大学 电子信息工程学院， 北京 100044)

当今世界已进入以信息化和智能化为主要特征的新工科时代，“信号与系统”课程是电子信息类专业重要的专业基础课程，为相关专业以及信息化和智能化提供了重要的基础理论。该课程主要阐述信号的时域分析和变换域分析，以及信号与系统的作用机理[1]。高校的根本任务是立德树人，课程思政是实现高校育德育智的重要举措[2-3]。该课程具有“原理深厚、方法多元、应用广泛”等特点，蕴含了丰富的课程思政元素，课程思政与课程教学深度融合，思想价值引领贯穿于课程教学全过程，启发了学生的辩证思维，熏陶了学生的探索精神，厚植了学生的家国情怀。

1 教学案例

没有信息化就没有现代化，而信息化的基础是数字化。信号的时域抽样正是阐述信号数字化的基本原理和方法，其架设了现实的模拟世界与虚拟的数字世界之间的桥梁，为信息化和智能化奠定了重要的理论基础。该案例的教学内容为“连续时间信号的时域抽样”。主要阐述“为何要进行信号抽样、信号抽样的理论分析、抽样定理的本质内容、抽样定理的工程应用”，其为连续信号的数字化分析与处理提供了理论支撑，是课程教学的重点内容之一。本讲内容的教学目标围绕知识传授、能力培养和价值塑造而展开。

2 思政元素

课程思政要以高质量的课程为基础，从而发挥专业课程承载的思政教育功能[4-5]。因此，面向信息时代发展，重塑“连续时间信号的时域抽样”的教学内容，深度挖掘该内容蕴含的思政元素，以先进的教学内容为载体，无痕融合思政元素，有效达成教学目标。

重塑教学内容，熏陶探索精神：科教融合，因时而新，重塑教学内容。在国内外同类教材中，修正了信号抽样的模型，揭示了抽样定理的本质内容，拓展了抽样定理的应用范畴。言传身教，引导学生勇于探索与创新。

正确对待得失，启发辩证思维：在信号抽样过程中，抽样间隔较大，则可能造成信号精度降低；若抽样间隔较小，则可能造成信号处理效率降低。因此，需要合理选择抽样间隔，正确处理精度与效率的辩证关系。

增强民族自信，厚植家国情怀：基于信号抽样定理，阐述了其在4G信号抽样以及铁道控制信号识别等方面的工程应用，展现了我国在通信和高铁领域，从跟随到引领的发展历程，增强学生强国有我的家国情怀。

3 教学设计

“信号与系统”课程在本科二年级上学期开设，处于专业课学习的入门适应阶段。该课程理论性强、概念抽象，学生擅长题型和计算，而对基本理论和分析方法的理解存在一定难度。此外，学生缺乏工程概念，难以综合所学知识去解决实际工程问题。基于学情分析，根植课程特点，提炼思政元素，思政铸魂课程教学，融情入理，实现知识传授、能力培养和价值塑造的协同推进。

(1)课程教学与思政教育同向同行，找准专业知识与思政内涵的契合点，思政理念无痕地贯穿课程“教学体系-教学内容-教学方法”，突出课程教学的思想性、前沿性和先进性，提升课程教学质量和育人效果。

(2)价值塑造与知识传授同频共振，思政元素融入课程的“基本原理-分析方法-工程应用”，潜移默化地将爱国情怀、科学素养、辩证思维、工匠精神等思政教育浸润教学全过程，实现育智与育德的有机融合。

(3) 思政能力与专业水平同步提升，名师引领，课程组教师集体备课、共同研讨、共建资源，提升专业课教师的思政育人能力和教学水平，确保课程思政的有效实施，促进课程教学和课程思政的可持续发展。

4 教学实践

该讲内容涉及连续与离散、时域与频域、理论与应用等诸多内容，根据学生认知特点，该讲教学内容将综合运用启发式、案例式、探究性等教学方法，线上线下有机结合，按照“为什么、是什么、做什么”的内在逻辑，以及提出问题、分析问题、解决问题的认知路径，引导学生由“知”内化为“识”，进而付诸于“行”，锻炼学生的高阶思维能力。注重师生互动和生生互动，引导学生自主性学习和探究。表1为精简的教学实施过程。

5 结语

探索实践了“信号与系统”课程思政的教学案例，课程思政是实现育德育智的有效途经，课程思政应实现课程教学内容与思政育人的同步推进。在教学过程中，课程教学内容是根本，思政内涵是灵魂。既要避免教学内容陈旧，更要避免思政元素的滥用和融入方式的生硬。该教学案例只是课程思政的初探，课程思政任重而道远。

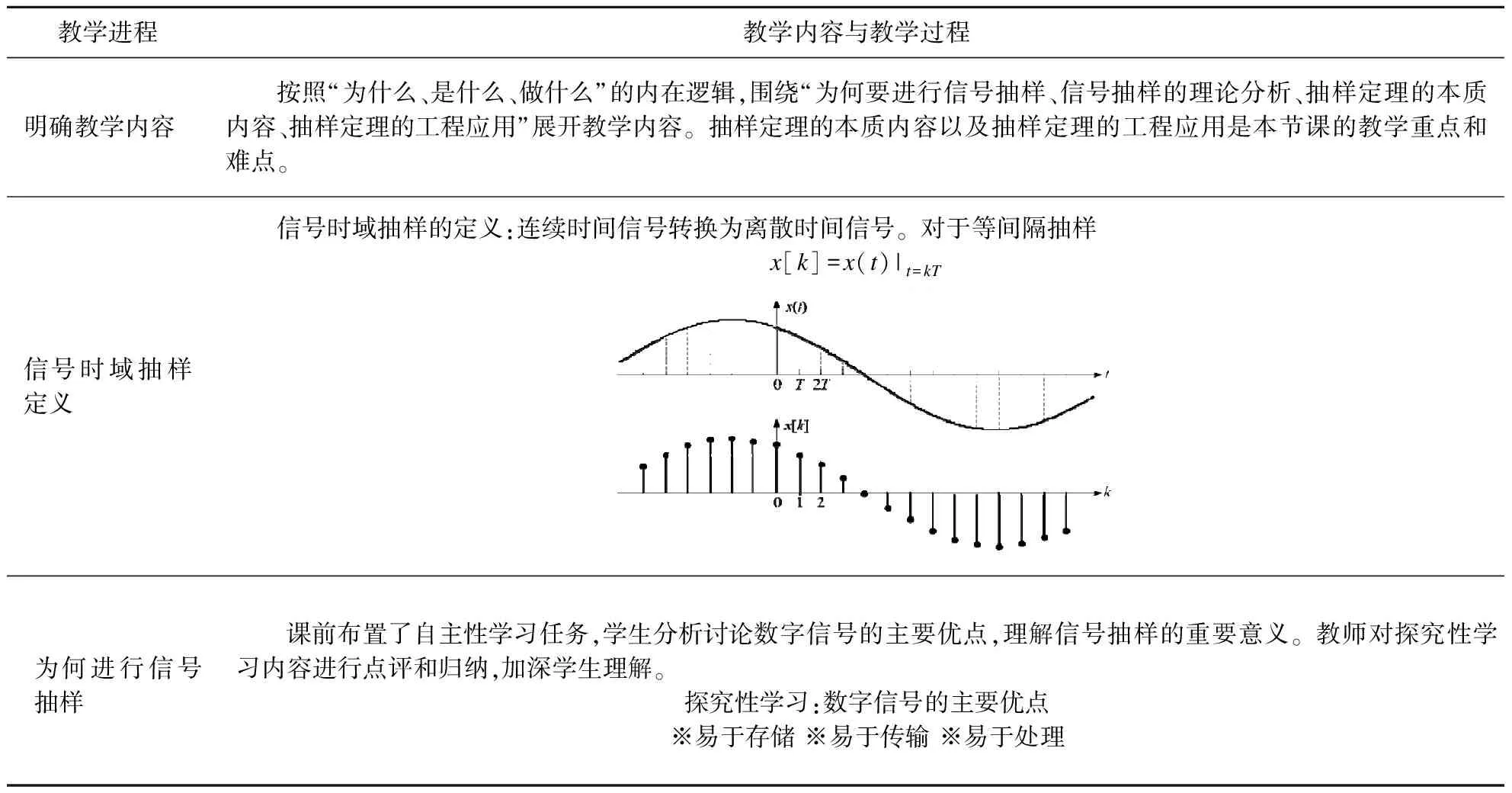
表1 教学实施过程

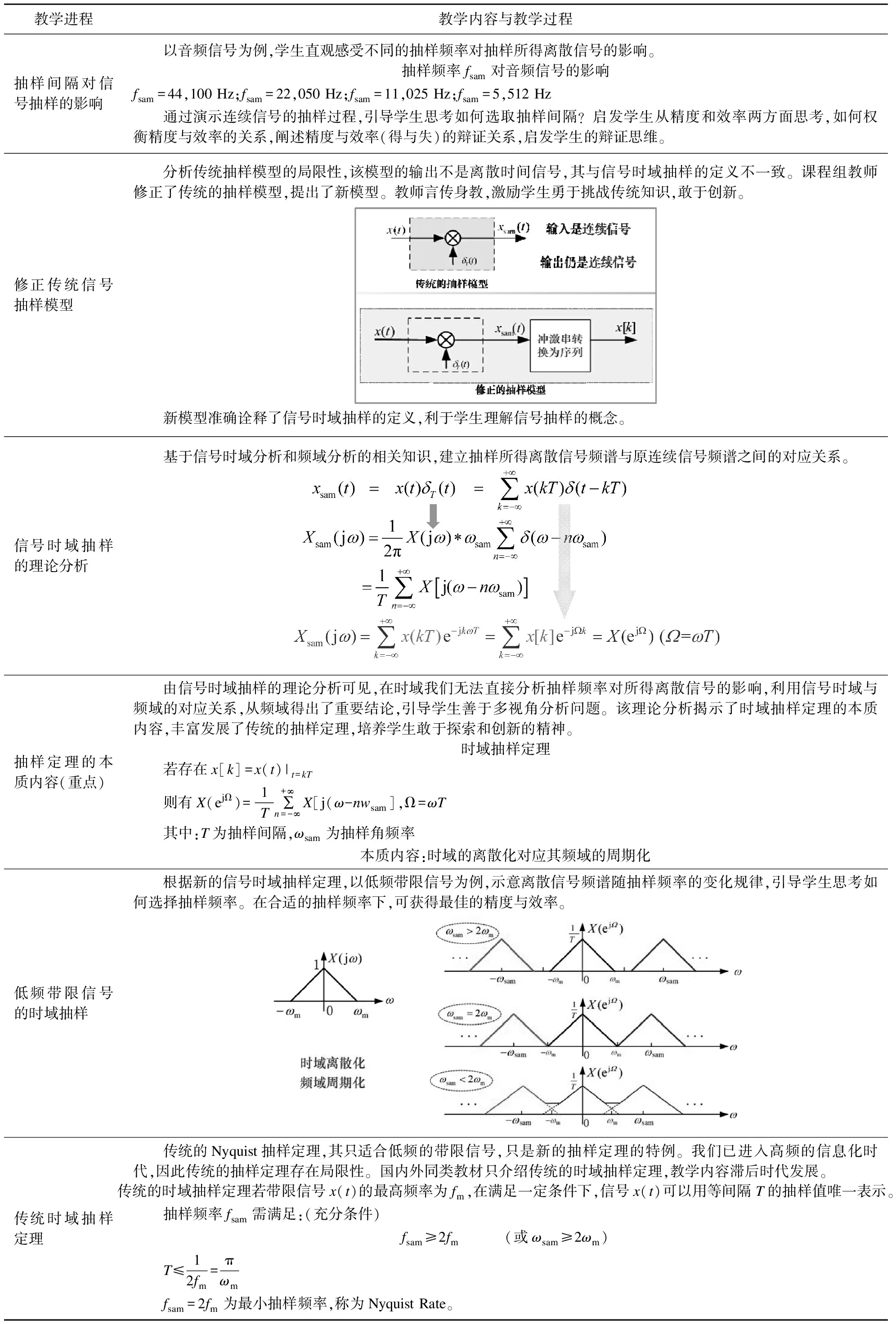
教学进程教学内容与教学过程抽样间隔对信号抽样的影响 以音频信号为例,学生直观感受不同的抽样频率对抽样所得离散信号的影响。抽样频率fsam对音频信号的影响fsam=44,100 Hz;fsam=22,050 Hz;fsam=11,025 Hz;fsam=5,512 Hz通过演示连续信号的抽样过程,引导学生思考如何选取抽样间隔?启发学生从精度和效率两方面思考,如何权衡精度与效率的关系,阐述精度与效率(得与失)的辩证关系,启发学生的辩证思维。修正传统信号抽样模型 分析传统抽样模型的局限性,该模型的输出不是离散时间信号,其与信号时域抽样的定义不一致。课程组教师修正了传统的抽样模型,提出了新模型。教师言传身教,激励学生勇于挑战传统知识,敢于创新。新模型准确诠释了信号时域抽样的定义,利于学生理解信号抽样的概念。信号时域抽样的理论分析 基于信号时域分析和频域分析的相关知识,建立抽样所得离散信号频谱与原连续信号频谱之间的对应关系。抽样定理的本质内容(重点) 由信号时域抽样的理论分析可见,在时域我们无法直接分析抽样频率对所得离散信号的影响,利用信号时域与频域的对应关系,从频域得出了重要结论,引导学生善于多视角分析问题。该理论分析揭示了时域抽样定理的本质内容,丰富发展了传统的抽样定理,培养学生敢于探索和创新的精神。时域抽样定理若存在x[k]=x(t)|t=kT则有X(ejΩ)=1T∑+∞n=-∞X[j(ω-nwsam],Ω=ωT其中:T为抽样间隔,ωsam为抽样角频率本质内容:时域的离散化对应其频域的周期化低频带限信号的时域抽样 根据新的信号时域抽样定理,以低频带限信号为例,示意离散信号频谱随抽样频率的变化规律,引导学生思考如何选择抽样频率。在合适的抽样频率下,可获得最佳的精度与效率。传统时域抽样定理 传统的Nyquist抽样定理,其只适合低频的带限信号,只是新的抽样定理的特例。我们已进入高频的信息化时代,因此传统的抽样定理存在局限性。国内外同类教材只介绍传统的时域抽样定理,教学内容滞后时代发展。传统的时域抽样定理若带限信号x(t)的最高频率为fm,在满足一定条件下,信号x(t)可以用等间隔T的抽样值唯一表示。抽样频率fsam需满足:(充分条件)fsam≥2fm (或ωsam≥2ωm)T≤12fm=πωmfsam=2fm为最小抽样频率,称为Nyquist Rate。