精心研究五题型轻松求解三角形
安徽省枞阳县宏实中学 朱贤良 246700
安徽省枞阳县教育教学研究室 徐维武 246700
“解三角形”这一板块知识涵盖了求三角形的边、角、面积、三角函数值以及诸多知识的综合运用等问题,既是初中解直角三角形内容的直接延伸,也是三角函数和平面向量知识考查的重要载体,同时也是解决三角形中的数量关系以及天文、地理及航海等生产生活实际问题的重要工具.
解三角形问题能很好地考查三角函数中的基本概念、公式、定理,并有效检测考生的逻辑推理、直观想象、数学运算、数学建模等核心素养,因而在历年高考中都占有重要地位.综观高考中的解三角形试题,其命题形式丰富多样,既体现基础性又突出综合性,题目的类型、所用到的方法、所体现的规律是非常值得总结的.结合对近些年高考试题的分析,本文拟对解三角形中常见问题的类型与求解方法作一初步的归纳,力求达到以少胜多、提高效率的目的.
1 知三求三问题
三角形有三条边与三个角等六个要素,根据边角中的三个可求其余三个(已知三角除外),此即解三角形中的知三求三问题.具体来说,知三求三问题可根据已知条件的不同分为以下五类:(1)已知三边求三角,先由余弦定理求某一角,再由余弦定理或正弦定理求其余两角.(2)已知两边及夹角求其余要素,先由余弦定理求第三边,再由余弦定理或正弦定理求其余两角.(3)已知两边及其中一边的对角求其余要素,先由余弦定理求第三边,或先由正弦定理求第二个角,再由余弦定理或正弦定理求其余边与角.需要注意的是,此类问题最多会有两组解.(4)已知两角及公共边求其余要素,先由三角形内角和定理得到第三角,再由正弦定理求其余两边.(5)已知两角及其中一角的对边求其余要素,同上一类问题,先由三角形内角和定理得到第三角,再由正弦定理求其余两边.
例1(2018 年高考全国Ⅰ卷·理17)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求 cos ∠ADB;(2)若,求BC.
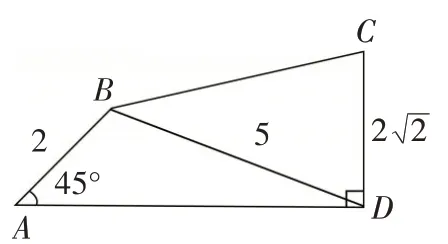
图1

评注:在求解知三求三类型的问题时,需要搞清楚已知什么,需要求的是什么,以便选择合适的求解思路.
例2(2013 年高考全国Ⅰ卷·理17)如图2,在△ABC中,∠ABC=90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°.(1)若,求PA;(2)若∠APB=150°,求tan ∠PBA.
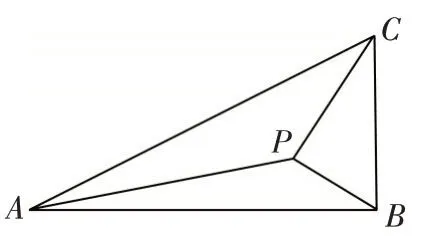
图2


评注:当图形中的三角形较多时,要注意分析条件,观察哪些三角形可解,哪些三角形不可解,由此探寻求解思路.
2 边角互化问题
三角形中的边角转化原则是通过统一边与角实现化繁为简,化未知为已知.一方面考虑化边为角,从而将问题转化为三角函数问题;另一方面考虑化角为边,从而将问题转化为代数变形问题.一般来说,当题目条件所给的是边或者正弦为齐次式时,可以运用正弦定理进行转化;当出现边的二次或者两边之积时,符合余弦定理的特征,则可考虑用余弦定理进行边角转化.
例3(2017 年高考全国Ⅱ卷·文16)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B= _____.
解析:条件中的已知式“2bcosB=acosC+ccosA”既可以考虑化边为角,也可以考虑化角为边,因此有两个思路.
思路1:化边为角
由正弦定理化边为角:2bcosB=acosC+ccosA⇒2 sinBcosB=sinAcosC+sinCcosA,即2 sinBcosB=sin(A+C),即2 sinBcosB=sinB,即cosB=,故B=.
思路2:化角为边

评注:遇到边角关系式,到底是统一成边(代数恒等变形),还是统一成角(三角恒等变换),可以根据题目的设问进行适当选择,实现优化解题.
例4(2019 年高考全国Ⅰ卷·理17)△ABC的内角A,B,C的对边分别为a,b,c.设(sinB-sinC)2=sin2A-sinBsinC.(1)求A;(2)若a+b=2c,求sinC.
解析:注意到条件式“(sinB-sinC)2=sin2A-sinBsinC”中的正弦为齐次式,应当考虑化角为边.


评注:利用边角转化解题的关键是要仔细分析题目条件与结论的结构特征,先预判,再选择合理的转化策略.
3 三角形面积问题
三角形面积的计算途径较多,如割补法、海伦-秦九韶公式等,但在高考数学试题中的考查主要有二个:一是小学时即熟知的“底与高乘积的一半”;二是用三角形的边角表示面积.在具体问题中,要结合题目的已知条件来选择合适的面积公式.
例5(2018 年高考全国Ⅰ卷·文16)△ABC的内角A,B,C的对边分别为a,b,c.已知bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为_____.
解析:本题是求△ABC的面积,这就需要对已知条件进行等价变形,以确定三角形面积的计算公式.


评注: 本题选择公式S=bcsinA来计算三角形的面积,是基于对条件中的两个等式的变形分析.
例6(2015 年高考全国Ⅱ卷·理17)如图3,在△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.
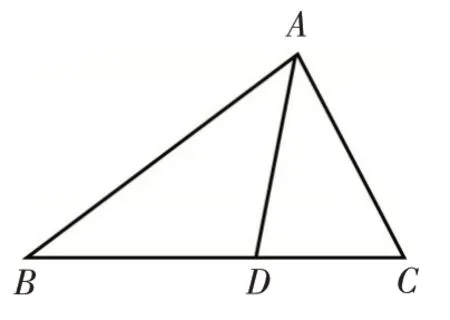
图3
解析: 本题的条件中未给出边长与角度及其关系,仅给出了角平分线分割出的两个三角形面积之间的关系S△ABD=2S△ADC.如何理解这一面积间的关系并作适当转化,是求解问题的关键.

思路2:用边与角来表示面积

评注: 在本题的求解过程中,合理地选择了三角形面积的计算方法,就是找到了正确的切入点与突破口.
4 最值范围问题
在解三角形的背景下,设置与边长、角度、周长、面积等相关的最值与取值范围问题,成为十分常见的命题角度.这类问题注重与函数、不等式和几何等知识的交汇融合,求解时需要充分利用正余弦定理、面积公式、三角形的内角和定理,并结合平面几何、基本不等式以及函数值域与最值等知识来实现破解.
例7(2011年高考全国课标卷·理16)在△ABC中,B=60°,,则AB+2BC的最大值为________ .

评注: 运用函数思想解决此类问题有两个关键步骤,一是合理选择自变量以建立函数关系;二是准确求解函数值域或最值.
例8(2019 年高考全国Ⅲ卷·理18 文18)△ABC的内角A,B,C的对边分别为a,b,c.已知asin=bsinA.(1)求B;(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
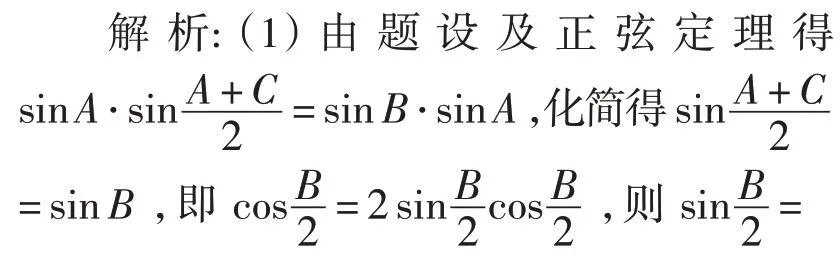

评注: 先根据正弦定理化角为边,再利用余弦定理和均值不等式,求得cosC的最小值,体现了转化与化归的数学思想.
例10(2015 年高考新课标全国Ⅰ卷·理16)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是_____.
解析: 作为一道解三角形问题,首要的问题是弄清“三角形”在哪里,即解哪一个三角形,故考虑连接四边形的任一对角线.如图4,在△ABC中,BC=2,∠B=75°,用解三角形知识与函数思想可求AB的取值范围.换个角度,我们也可以尝试从画图的角度来确定AB的变化规律.如图5,先画定线段BC=2,继而以BC为公共边作∠B=∠C=75°,再在∠B的另一边上选一点A,作∠BAD=75°交∠C另一边于点D,即得与题意相符的四边形ABCD.显然点A在线段A1A2上运动(不含两端点).

图4

图5

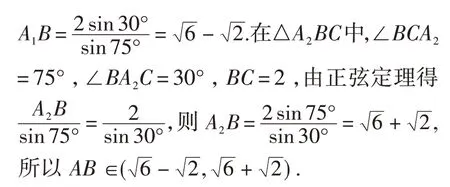
评注: 取值范围与最值问题最普遍的求解方法是利用函数思想,如思路1,关键在于合理选择自变量,进而构建函数关系式,解法厚重而大气;思路2从运动的角度入手,着重理清点A的运动轨迹,直观而轻盈.
5 实际应用问题
在生产和社会生活中,很多时候都需要测量距离、高度和角度等数学量,尤其是在物理、航海和工程技术方面,均有解三角形的运用.求解三角形实际应用问题时,我们可抽象出数学模型,然后正确使用正余弦定理去解决.
例11(2009 年高考海南宁夏卷·理17)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图6),飞机能够测量的数据有俯角和A,B间的距离.请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤.
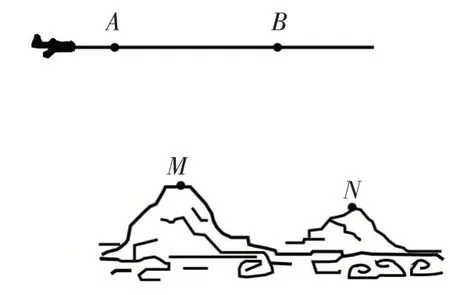
图6
解析: 计算M,N间的距离,首要的是以MN为边构建三角形.结合飞机能够测量的数据包括俯角和A,B间的距离,故考虑连接AM,AN,BM,BN,MN,如图7 所示.这样,通过解图7中的三角形即可求得M,N间的距离.①需要测量的数据:点A到点M,N的俯角α1,β1,点B到点M,N的俯角α2,β2,A,B两点间的距离d.②计算M,N间距离的步骤:
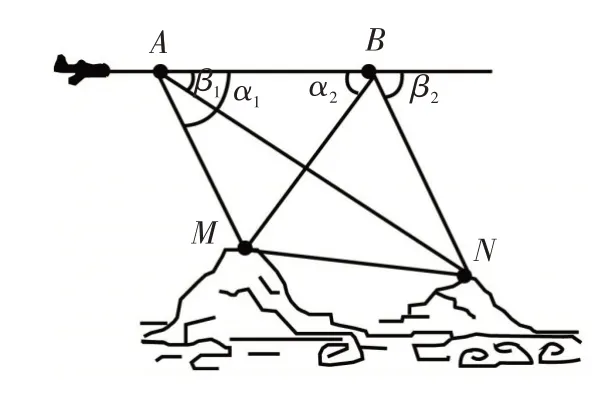
图7

评注: 本题让考生拟定测量方案,与传统计算型问题相比,更能有效考查考生分析、解决问题的能力,让人耳目一新.
例12(2013 年高考江苏卷·18)如图8,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C,另一种是先从A 沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50mmin,在甲出发2 min 后,乙从A 乘缆车到B,在B处停留1 min 后,再从B 匀速步行到C.假设缆车匀速直线运动的速度为130mmin,山路AC 长为1260 m,经测量,cosA=,.(1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3 分钟,乙步行的速度应控制在什么范围内?

图8


评注: 本题来源于生活,来源于教材,但又髙于教材,考査学生对知识的综合应用能力.在解三角形和分式不等式、绝对值不等式交汇处命题,同时要求学生具有较强的数学建模能力.

