求解体制转换模型下美式期权定价问题的投影收缩算法

高子涵, 黄存昕, 宋海明, 周搏成

(吉林大学 数学学院, 长春 130012)

0 引 言

由于标准的美式期权无法准确解释由短期政治或经济不确定性而引起的周期性变化, 因此关于体制转换下的期权定价模型研究得到广泛关注. 假设标的资产S在ρ种体制下满足随机微分方程

(1)

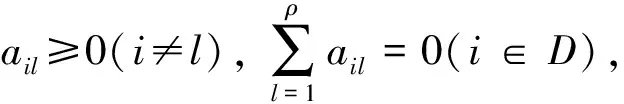
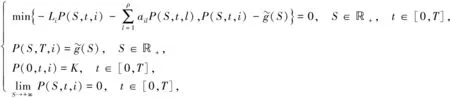
(2)

(3)

与传统美式期权定价问题类似, 体制转换模型(2)在每种体制下都存在一条最佳实施边界, 记为Bi(t).由于最佳实施边界的存在以及不同体制下期权价格的耦合关系, 使变分不等方程(2)成为高度非线性变系数问题, 又因为该问题的求解区域无界, 因此很难给出高精度的数值算法.针对上述问题, 本文先利用相应的变量替换和远场截断技巧将原问题简化为有界区域上的非线性问题, 再针对得到的非线性问题设计去除非线性影响的半隐式差分格式, 最后采用投影收缩算法(简称PCM算法)对离散系统进行快速求解.

1 模型简化

下面以两种体制下的美式看跌期权为例进行讨论.首先通过变量替换[2]

t=T-τ,S=exp{x}，

(4)

将变系数方程(2)转化为常系数形式:

(5)

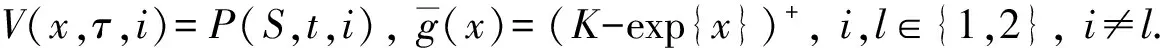
进一步, 令V(x,τ,i)=W(x,τ,i)exp{αiτ+βix}[3], 其中

则方程(5)可简化为

(6)

其中g(x,τ,i)=exp{-αiτ-βix}(K-exp{x})+,ξ=α2-α1,η=β2-β1.

由于简化模型(6)是定义在无穷区域上的抛物型变分问题, 直接截断求解区域会导致数值解不稳定或不精确, 因此本文将给出合理的截断策略.

引理1[4]当σ1≥σ2,r1=r2时, 有

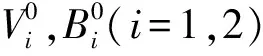
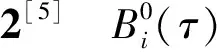
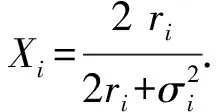
KX≤Bi(τ)≤K,Bi(0)=K，

其中X=min{X1,X2}.

引理3[5]给定ε∈(0,1), 则有

其中

进一步, 若r1=r2, 则有

Vi(x,τ)≤ε, ∀x≥L0, 0<τ≤T,

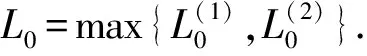
根据引理1中关于期权价格和最佳实施边界的估计式, 当r1=r2时, 可将变分不等问题(6)的求解区域进行截断， 并给出合理的边界条件.由标准看跌期权的性质可知, 当S≤Bi(t)时,Vi(x,t)=(K-S)+.因此, 对于左边界, 根据引理2, 只要满足截断位置小于等于KX, 即可给出变分不等问题(2)的精确边界条件, 进而在x≤ln(KX)处截断, 便能给出变分不等问题(6)在左边界处的精确边界条件.根据引理3, 当给定足够小的误差限ε后, 变分不等问题(6)便可在x≥L0处截断并设置0边值条件.为叙述方便, 本文取L=max{-ln(KX),L0}作为截断长度, 截断后的求解区域用[-L,L]表示.因此， 有如下命题.

命题1给定ε∈ (0,1), 令L= max{-ln(KX),L0}.在满足引理1的条件下, 取截断长度为L, 则变分不等问题(6)左边界条件精确成立, 右边界估值合理.

基于上述讨论, 问题(6)可化为如下有界规则区域上的线性互补问题:

(7)

至此, 已将无界区域上非线性问题(2)转化为有界区域问题(7).

2 数值解法

首先考虑对线性互补问题(7)进行半隐式差分离散, 然后设计求解离散系统的PCM算法.在进行数值离散前, 先给出一些符号.假设时间剖分和空间剖分分别为

此时可将方程(7)转化为如下离散形式：

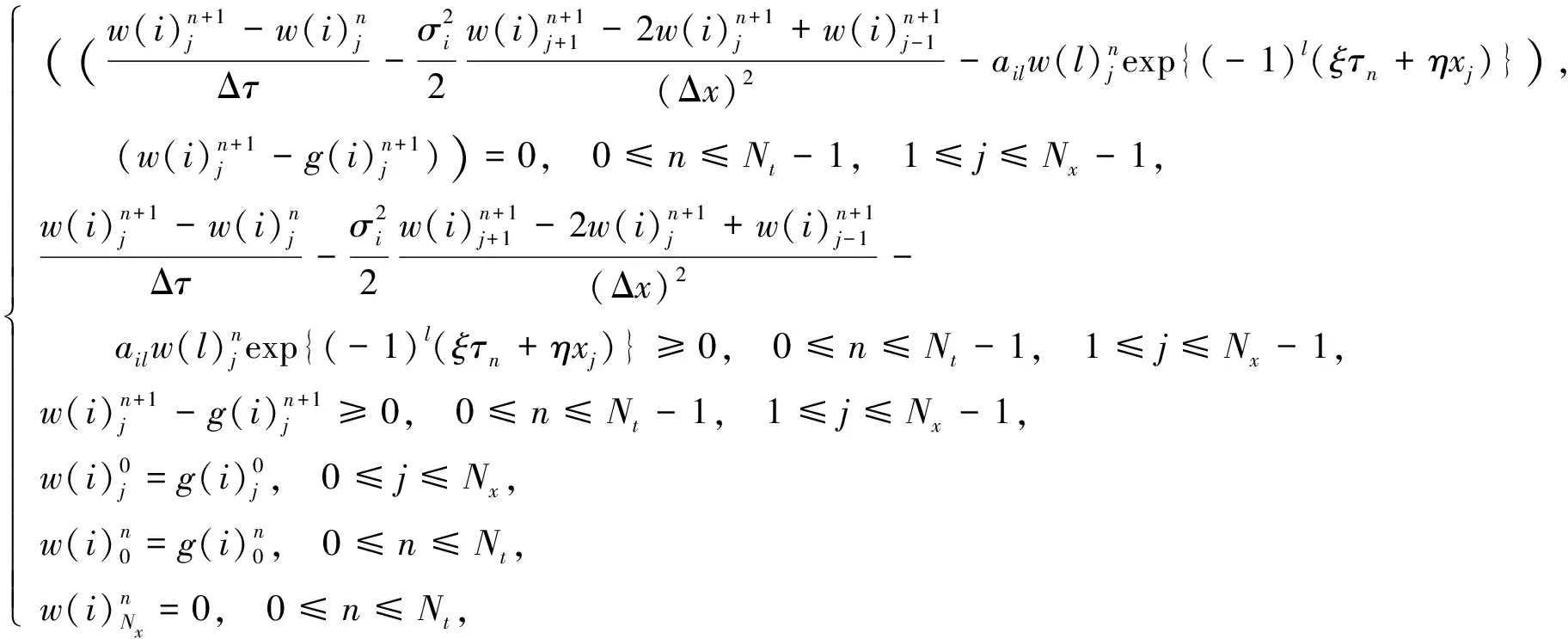
(8)

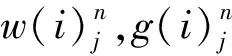
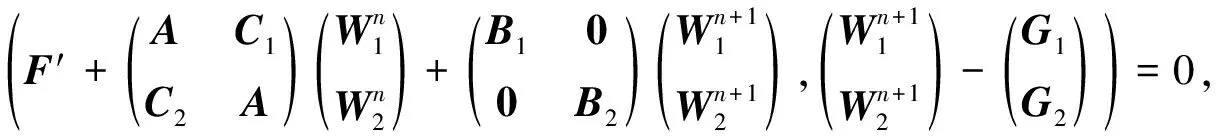
(9)

其中

Ci=-Δτaildiag(exp{(-1)l(ξτn+ηxj)}), 1≤j≤Nx-1,

记

则式(9)可改写为

(MΦ+F,Φ-G)=0.

(10)

同理式(8)中的约束条件可简写为

MΦ+F≥0,Φ-G≥0.

(11)

定理1约束条件(11)中的矩阵M对称正定.

证明: 对称性显然, 下证正定性.由矩阵M的定义可知,M为严格对角占优矩阵.设λ为矩阵M的任一特征值, (mij)为矩阵元素, 根据Gerschgorin定理[6]有

λ≥mi,i- |mi,i-1|-|mi,i+1|>0.

(12)

由对称性及特征值全部为正数可知, 矩阵M是一个对称正定矩阵.

由文献[7]可知, 若矩阵M对称正定, 则线性互补问题(10),(11)解存在唯一, 进而可得本文离散系统解的存在唯一性.

定理2离散格式(8)稳定, 即‖Φn+1‖∞≤C‖Φ0‖∞.

从而有

‖Φn+1‖∞≤(1+Δτailexp{(-1)l(ξτn+ηxj)})‖Φn‖∞.

(13)

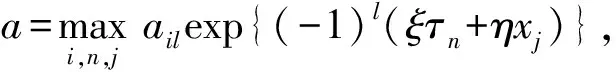
‖Φn+1‖∞≤(1+Δτa)‖Φn‖∞.

因为max{exp{-αiΔτ},1+aΔτ}n+1=max{exp{-αiΔτ(n+1)},(1+aΔτ)n+1}, 所以有

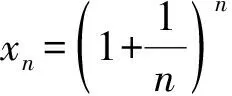
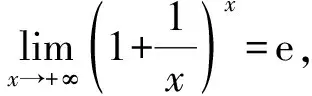
令C=max{exp{-αiT},exp{aT}}, 则可得结论.证毕.

3 PCM收敛性分析

考虑线性变分不等问题(LVI):

(V-Φ)T(MΦ+F)≥0,Φ∈Ω, ∀V∈Ω.

(14)

当Ω={Φ∈n|Φ≥0}时, 线性互补问题(LCP)是一个特殊的(LVI)问题, 其中(LCP)问题为

Φ≥0, (MΦ+F)≥0,ΦT(MΦ+F)=0.

(15)

故可借助(LVI)问题的性质研究(LCP)问题的性质. 下面针对(LVI)问题的PCM算法给出收敛性分析.

(LVI)问题等价于下列线性投影问题[8]：

e(Φ)=Φ-PΩ[Φ-(MΦ+F)].

(16)

对给定的Φ0∈n, 如果Φk∉Ω*, 则定义迭代Φk+1=Φk-ρ(Φk)d(Φk), 上行方向

d(Φk)=(MT+I)e(Φk),

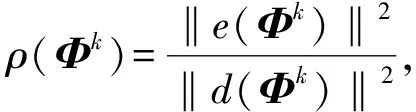
设问题(14)的解集为Ω*, 由PCM算法的定义, 可得如下引理.

引理4[8]任取Φ*∈Ω*, 则(Φ-Φ*)T(I+MT)e(Φ)≥‖e(Φ)‖2, ∀Φ∈n.

引理5[8]由PCM算法产生的序列{Φk}满足

‖Φk+1-Φ*‖2≤‖Φk-Φ*‖2-ρ(Φk)‖e(Φk)‖2, ∀Φ*∈Ω*.

‖Φk+1-Φ*‖2≤‖Φk-Φ*‖2-c‖e(Φk)‖2, ∀Φ*∈Ω*.

(17)

式(17)表明‖e(Φ)‖是测量Φ与Ω*之间距离的函数, 如果‖e(Φ)‖较大, 则每次迭代可以向解集近一步, 如果‖e(Φ)‖较小, 则表明Φk能很好地近似Ω*中的一个解Φ*.根据文献[8]中的收敛性理论可给出如下定理.

定理3由PCM算法产生的序列{Φk}收敛于解集Ω*中的某个解Φ*, 且当Ω={Φ|Φ≥0}时, {Φk}全局线性收敛于Φ*∈Ω*.

则序列{Φk}有界.此外, 由式(17)可得

且有

令Φ*是{Φk}的一个聚点且有子列{Φkj}收敛于Φ*.因为e(Φ)连续, 故有

即Φ*是(LVI)问题的一个解.因为Φ*∈Ω*, 且

‖Φk+1-Φ*‖≤‖Φk-Φ*‖,

(18)

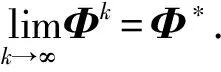
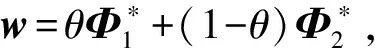
(20)

式(19)和式(20)相加, 则有

(Φ-w)(I+MT)e(Φ)≥‖e(Φ)‖2.

令Φ=w, 则有e(w)=0, 即w∈Ω*, 故Ω*是一个闭凸集.因为{Φk}收敛到一个解Φ*, 且

{Φk}⊂{Φ∈n|‖Φ-Φ*‖≤‖Φ0-Φ*‖},

由式(17),(18)可知

(21)

其中0<1-cη2<1, 即满足全局线性收敛.

4 数值实例

考虑对一年期(T=1)美式看跌期权定价问题(2)进行数值模拟, 对于方程(2), 选取文献[2]中的参数：

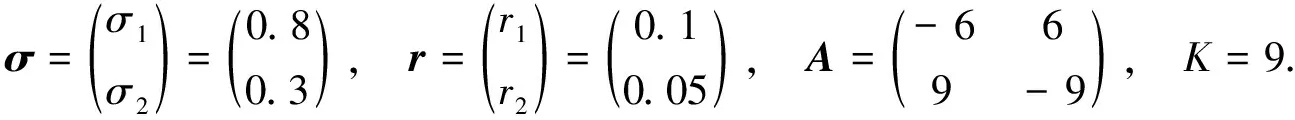
(22)

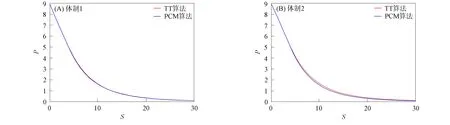
图1 不同体制模型下PCM算法与TT算法求得的期权价格二维图像对比Fig.1 Comparison of two-dimensional images of option prices obtained by PCM algorithm and TT algorithm under different regime models

虽然文献[2]指出式(22)中r1≠r2, 但本文截断技巧仍然有效.在命题1中, 取ε=10-6, 可得截断边界L=7.494 8.在差分离散中, 取时间分划份数Nt=800, 空间分划份数Nx=600.在PCM中, 取ν=0.9,μ=0.1,ρ=1.9.则在上述参数设定下, PCM算法求得的期权价格与三叉树算法(简称TT算法)求得的期权价格对比结果如图1所示. 由图1可见, PCM算法求解的期权价格与TT算法求解结果非常接近, 表明了本文算法的正确性. 当Nt=500,Nx=300时, TT算法的运算时间约是PCM算法的15倍, 证明了PCM算法的有效性. PCM算法求得期权价格的三维图像如图2所示.

图2 不同体制模型下PCM算法求得期权价格的三维图像Fig.2 Three-dimensional images of option prices obtained by PCM algorithm under different regime models

综上, 本文研究了体制转换下美式期权定价问题的数值解法. 首先通过分析体制转换美式期权与传统美式期权在价格和最佳实施边界上的关系, 给出合理的区域截断策略和边界条件, 将其转化为有界区域上的线性互补问题; 然后针对线性互补问题的结构, 采用半隐式差分格式进行数值离散, 并给出差分格式的稳定性证明; 最后根据离散系统的特点, 采用PCM算法进行求解, 给出了该算法的收敛性分析, 并通过数值模拟验证了PCM算法的有效性.