带分布时滞分数阶微分方程非振动解的存在性

赵环环, 刘有军, 康淑瑰

(山西大同大学数学与统计学院，大同 037009)

0 引言

鉴于分数阶微分方程在流体力学、化学物理、电子网络、动力系统控制理论、流体流动和经济学等领域的有广泛的应用。近十几年人们又加快了对分数阶常微分和偏微分方程的研究，取得了一定的进展[1–2]。此外，整数阶泛函微分方程的振动理论由于其有重要的理论价值和现实意义，一直受到学者们的青睐，也得到了长足的发展[3–4]。与此同时，我们关注到学者们对一类中立型微分方程非振动解的存在性做了大量的研究工作[5–13]，通过对以上方程的发展历程来看，它们的中立型部分主要讨论的都是常时滞的，且主要研究思想是相似的。将中立型部分的系数分成四种情况来讨论，即(−∞,−1), (−1,0), (0,1), (1,+∞)，并针对每一种情况通过构造相应的算子来证明。然而，中立型部分带分布时滞的情形的相关文献不多。在2013 年，Candan[13]讨论了一阶中立型带分布时滞微分方程

这里γ是两个正奇数的比，但是他仅仅研究了系数是

的情形，没有给出其他三种情况的证明过程和结果。通过分析发现，产生这种情况的原因是按照已有的办法构造算子在推导过程中出现了较大的困难。综合以上，本文通过打破传统，构造出新的算子，成功的克服了这个困难，依然得到了方程的中立型部分系数∫b a p2(t,ξ)dξ在四种情况下非振动解的存在的充分条件，并且在近年来，我们注意到了分数阶微分方程振动性结果[14–18]，但带分布时滞分数阶微分方程的振动性论文较少。因此，研究该问题有其重要的理论价值和现实指导意义。

本文考虑分数阶中立型微分方程

Φ(u)定义在R 上，关于u的连续递增的实奇函数，且Φ−1(u)满足局部Lipischitz 条件。gi ∈C(R,R),gi(u)满足局部Lipischitz 条件，对u ̸=0，有ugi(u)>0,i=1,2。

本文将会用到以下定义、性质和记号。

定义1若方程(2)的一个解有任意大的零点，则称其为方程(2)的振动解，否则称为非振动解。

定义2若存在充分大的t1>t0，对于x(t)∈C([t1−µ,∞),R)，使得

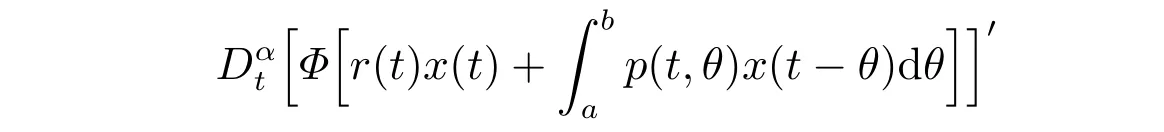
在[t0,∞)上存在，且满足方程(2)，则x(t)为方程(2)的解，这里µ=max{θ,d,f}。

定义3[1]在半轴上的刘维尔分数阶积分定义为

这里t ∈R,α ∈[0,∞)。

定义4[1]在半轴上的刘维尔分数阶导数定义为

这里n= [α]+1,α ∈[0,∞), [α]定义的是α的整数部分。特别地，如果α=n ∈N，则f(t)=f(n)(t)，这里f(n)(t)是f(t)在通常意义下的n阶导。

性质1[1]对α>0,λ>0，有

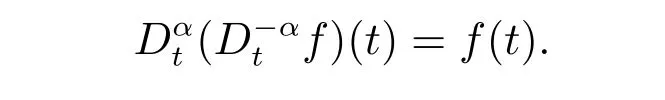
记Li分别是函数gi定义在集合A上的Lipischitz 常数，K是函数Φ−1(u)的Lipischitz常数，分别地

1 主要结果

定理1假设

且满足下面情形之一：

则方程(2)存在一个有界的非振动解。

证明 令Λ是所有定义在[t0,∞)上的具有上确界范数

的有界连续函数的全体，则易知Λ是一个Banach 空间。

情形(a)

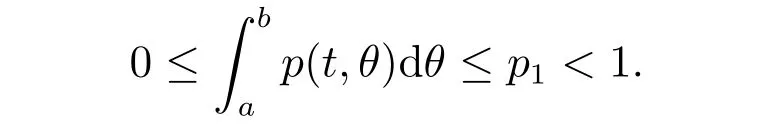
设A={x ∈Λ,M1≤x(t)≤M2,t ≥t0}，这里M1和M2是两个正常数，且使得

由方程(2)，选择t1≥t0+µ，当t ≥t1充分大时，使得

成立。接下来，在A上定义算子T如下

容易看出，T是连续的，对于t ≥t1,x ∈A，用(3)式，有

再用到(4)式，可得

这些表明TA ⊂A，由于A是Λ中有界的闭的紧集。为了应用压缩映像原理，我们必须说明T是A上的一个压缩算子。

对所有的x1,x2∈A，当t ≥t1时，有

这表明上确界范数

并且说明T是A上的一个压缩映射，则由Banach 压缩映像原理可得方程(2)存在唯一的正有界解∈A，使得T=，也就是

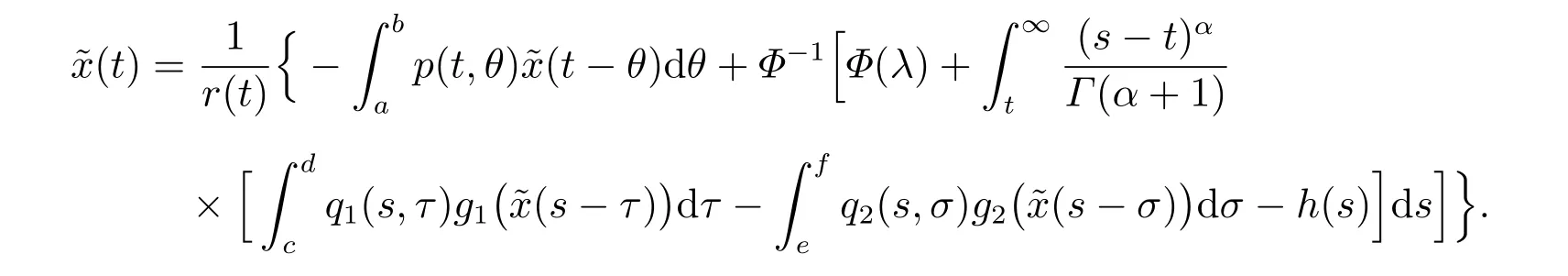
进一步，得

即有

根据性质1，容易看出˜x(t)是方程(2)的一个非振动解。

情形(b)

设A={x ∈Λ,M3≤x(t)≤M4,t ≥t0}，这里M3和M4是两个正常数，且使得

由(3)式，选择t1≥t0+µ，当t ≥t1充分大时，使得

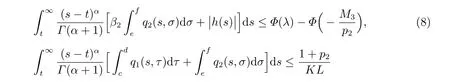
成立。接下来，在A上定义算子T如下

容易看出T是连续的，对于t ≥t1,x ∈A，用(7)式，我们有

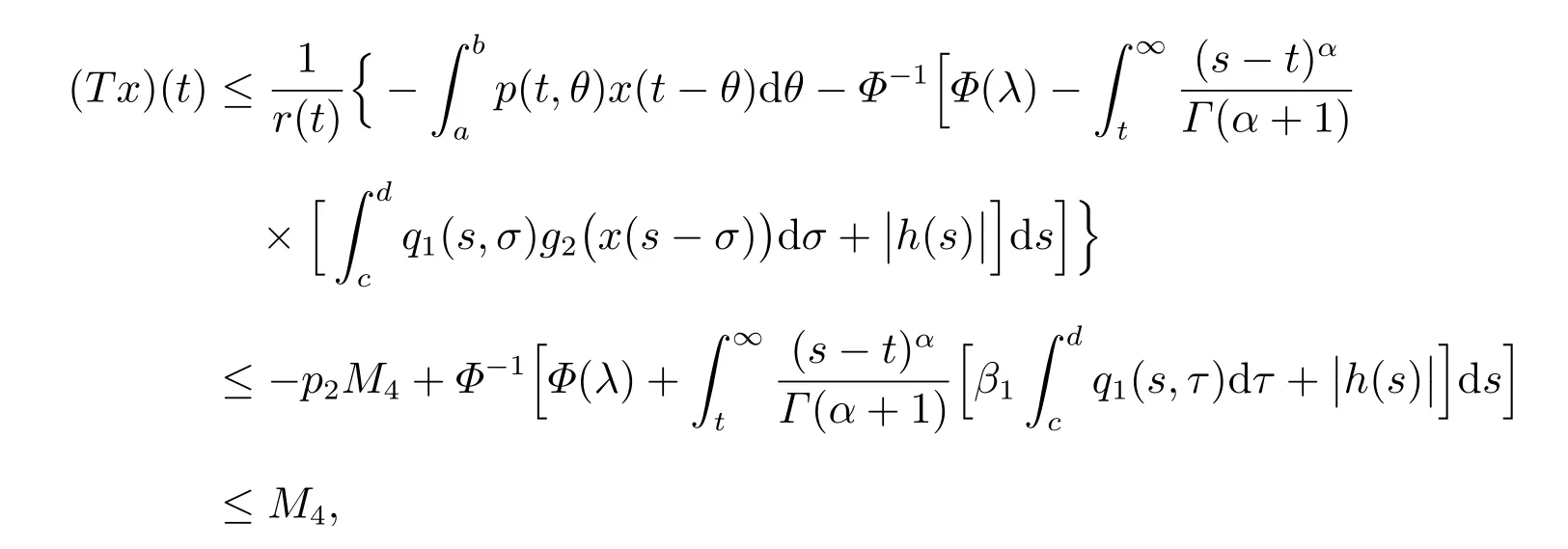
且利用(8)式，得

这些表明TA ⊂A，由于剩下的证明过程与情形(a)证明类似，故省略了。

情形(c)

设A={x ∈Λ,M5≤x(t)≤M6,t ≥t0}，这里M5和M6是两个正常数，使得

由(3)式，选择t1≥t0+µ，当t ≥t1充分大时，使得

成立。由于剩下的证明过程与情形(a)证明类似，故省略了。

情形(d)

令A={x ∈Λ,M7≤x(t)≤M8,t ≥t0}，这里M7和M8是两个正常数，且使得

由方程(2)，选择t1≥t0+µ，当t ≥t1充分大时，使得

成立。由于剩下的证明过程与情形(b)证明类似，故省略了。

注1当α=n=1∈N,r(t)≡1,Φ(u)=uγ,q2(t,σ)=0 和h(t)=0，方程(2)中立型部分变成了方程(1)的中立型部分，核心是本论文将中立型部分的系数p(t,θ)dθ由原来的(−1,1)拓展到(∞,−1)∪(−1,1)∪(1,+∞)。

2 算例

例1考虑分数阶带分布时滞微分方程

这里

容易看出

因此，定理中情形(b)成立。事实上，x(t)=e−t是方程(9)的一个非振动解。