体积约束的非局部扩散问题基于新的技巧的有限元方法

葛志昊, 吴慧丽

(河南大学数学与统计学院，开封 475004)

0 引言

连续介质力学中的非局部理论是由文献[1–3]提出的。近场动力学模型和非局部扩散模型都属于非局部理论的范畴，自Silling 在文献[3]中首次介绍近场动力学模型之后，其有效性已经在许多领域得到证明，如复合材料的断裂、多晶体的断裂、纳米纤维网络、裂缝的不稳定、图像处理等[4–6]。非局部模型是一个不涉及位移场空间导数的积分型方程，因此，非局部模型允许有跳跃间断点的解存在，并且可以用同一个非局部方程来描述间断点及非间断点处的物理过程，而不需要知道间断点的位置。此外，可以将非局部模型看作分子动力学的变形，它可以从微观上反映物理材料中粒子之间的相互作用，将连续力学与分子动力学联系起来[7]，克服了经典的连续模型只能从宏观的角度研究材料的结构性质和影响规律的缺点。对于近场动力学模型Cauchy 问题的适定性研究，可以参考文献[8–11]。特别是，文献[10,12]提出了一种非局部向量微积分计算和抽象的非局部平衡法则。此外，也有一些数值方法求解该问题，包括分片常数有限元方法、有限差分法、求积法和质点法等[13–16]。最近，文献[17]提出了分片常数有限元方法来解决非局部扩散问题。为了得到一种高阶数值方法，我们提出了一种高阶有限元方法来求解二维体积约束的非局部扩散问题，并采用一种新技巧计算线性元的刚度矩阵。值得一提的是，求解二维体积约束的非局部扩散问题并不是平凡的。

本文第1 部分，我们提出了体积约束的非局部扩散问题的有限元方法，给出了元素的编码原理和数值计算节点的编码表达式。此外，我们还采用了一种新的方法来计算刚度矩阵。最后，通过数值算例验证了理论计算结果。

1 基于新技巧的有限元方法

令Ω ⊆Rd(d= 2,3)表示一个有界连通开区域，且Ω=Ωs ∪ΩI，其中Ωs是解区域，ΩI是Ωs周围宽度为δ的限制区域。现在，我们列出了一些如下的符号，关于定义的细节和一些例子，可以参考文献[12]。

β=β(x,x′):Ω×Ω →R 为一个两点标量函数，并且满足：

注意，δ/2 可以用其他小于δ的适当的常数来代替，以保证β(x,x′)的非退化性。

令α=α(x,x′) :Ω×Ω →Ω ≤Rd是一个反对称两点向量函数满足α(x,x′)+α(x′,x) = 0。给定一个两点函数v :Ω×Ω →Ω ⊆Rd和一个点函数u:Ω →R，非局部散度算子D(v):Ω →R 和其共轭算子D∗(u):Ω×Ω →Ω ⊆Rd，定义如下

本文研究带有体积约束的非局部扩散问题

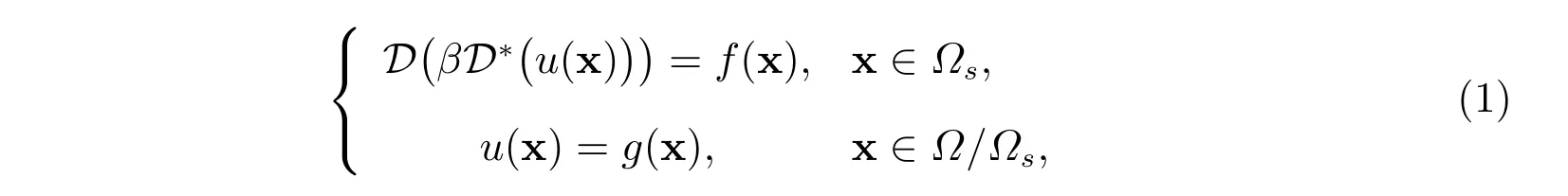
其中Ω=(−δ,1+δ)×(−δ,1+δ),Ωs=(0,1)×(0,1)。

问题(1)中的核函数用γ(x,y)来表示，即γ(x,y)=βα·α。若取

则有

将区域Ωs剖分成2N1N2(N1=N2=N)个三角形单元，从而得到步长

同时，以相同的步长对带状边界区域Ω/Ωs进行剖分，将区域Ω上的三角形剖分单元的集合记为P=∪{K}=P1∪P2，其中K为三角形剖分单元，P1是求解区域Ωs上三角形剖分单元的集合，P2是带状边界区域上Ω/Ωs三角形剖分单元的集合。

记Ω上有限元节点的指标集为N，Ωs上的有限元节点指标集为NI，Ω/Ωs上有限元节点的指标集为Nb，求解区域Ωs上的有限元节点总数为n= (N1+1)(N2+1)，区域Ω上有限元节点总数为n1。

设P和T分别是2×n和3×(2N1N2)的矩阵，矩阵P的第k列表示三角形剖分中整体编码是k的节点的坐标，矩阵T的第k列表示三角形剖分中编码是k的三角形剖分单元的三个顶点对应的整体编码。剖分节点的整体编码按照由左至右、由下至上的原则，三角形剖分单元上三个节点的局部编码按照逆时针的原则。例如，N1=N2= 2 时，每个三角形剖分单元上剖分节点的局部编码如图1，剖分节点以及三角形剖分单元的整体编码如图2。

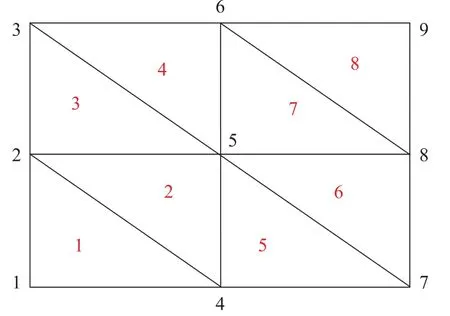
图2 剖分单元及节点的整体编码

下面采用线性有限元方法来求解非局部扩散问题(1)，V和V h ⊂V分别是非局部扩散问题(1)的解空间及有限元子空间。在参考三角形单元上三个顶点对应的节点局部基函数分别为

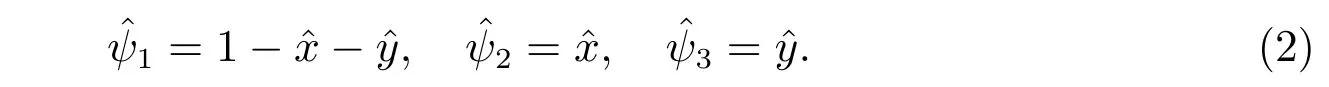
令Am1=(xm1,ym1)′,Am2=(xm2,ym2)′,Am3=(xm3,ym3)′。然后，根据参考单元与实际单元Km=△Am1Am2Am3之间的仿射变换关系式(2)，我们可以定义实际三角形剖分单元Km上三个节点对应的局部基函数ψmi(x,y)=,i=1,2,3，其中

|Jm|=(xm2−xm1)(ym3−ym1)−(xm3−xm1)(ym2−ym1)为Jacobi 矩阵的行列式。因此，整体线性基函数ϕi满足

记ϕi≜ϕi(x)，则非局部扩散问题(1)的变分形式及有限元逼近的一般形式分别是：求u(x)∈V和uh(x)∈V h，使得

其中

uj表示在节点xj处的数值解的值。

令v(x)=ϕi(x),i ∈NI，并且利用式(4)，则有

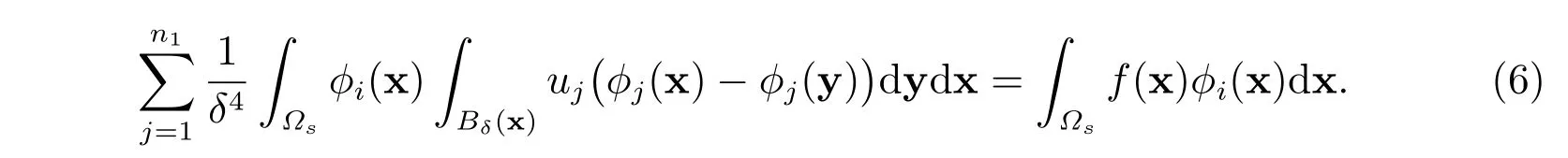
因此，有

其中C(NI)和C(Nb)分别是NI和Nb索引集的元素的个数，i,j ∈NI,m ∈Nb。然后，得到线性代数系统

其中刚度矩阵A 为

在式(9)中，矩阵A1很容易用通常的方法进行计算，矩阵A2可以计算如下

首先，从式(10)取j ∈N 和i ∈NI。然后，可以得到一个n×n1矩阵

其次，从矩阵B中选取包含ϕj(y)(j ∈Nb)的元素，矩阵B的其余元素保留并表示为B1，而新矩阵B1恰好就是A2(i,j ∈NI)。据我们所知，这是第一次用B来计算A2。

采用与文献[18]相似的论证方法，得到如下结论，此处不再详细证明。

定理1如果存在常数s ∈(0,1)，以及γ∗和γ∗，使得

且u ∈V ∩Ht+1(Ω)，则对于足够小的h，存在一个常数C，使得

2 数值算例

我们考虑以下二维非局部扩散问题

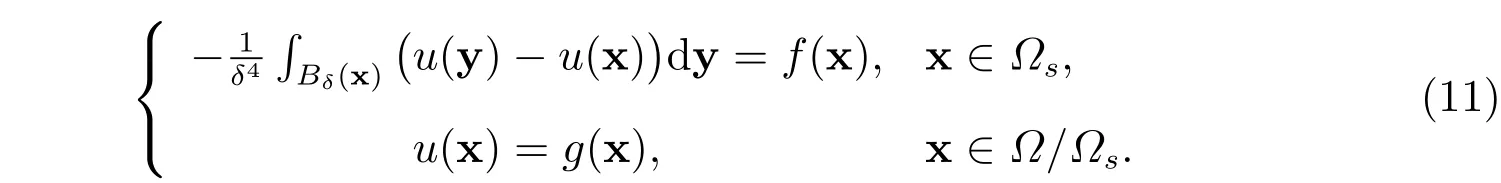
取Ωs=(0,1)×(0,1),Ω=(−δ,1+δ)×(−δ,1+δ)，选择真解为u(x)=x2+y2，则f(x) =和g(x)可以相应的计算得出。表1给出了L2范数误差和H1半范数误差，其中N为x(或y)方向等分的份数。

表1 δ =0.2

从表1 中可以看出，当网格尺寸H变小时，对于分片线性元，L2范数的误差收敛阶为2，H1范数的误差收敛阶为1，而文献[17]中P0元的L2范数和H1范数的误差收敛阶都是0.5。因此，可以说本文所设计的方法的收敛阶几乎是最优的。从图3 中我们看到，当网格尺寸h变小时，数值解更接近真实解。

图3 δ =0.2 时的精确解和数值解

3 结论

本文针对二维体积约束的非局部扩散问题提出了一种基于新技巧的高阶有限元方法，该数值方法的刚度矩阵由一个新的矩阵B提取，该矩阵易于计算。据我们所知，用矩阵B来计算A2这是第一次，本文给出了元素的编码原理和数值计算节点的编码表达式。同时，通过数值算例，验证了对于体积约束的非局部扩散问题中线性有限元方法的误差L2范数的收敛速阶达到2，H1半范数的收敛速阶几乎为1。在今后的工作中，将用本文的数值方法来处理Pk(k ≥2)元素。