带状态依赖时滞微分方程的周期与几乎周期解的应用

周 辉, 王 文

(合肥师范学院数学与统计学院，合肥 230601)

0 引言

在过去四五十年，由于带状态依赖时滞的泛函微分方程常被用来描述许多模型动力学[1–2]，从而，此类系统引起了人们的研究兴趣。关于带状态依赖时滞的泛函微分方程的研究在解的存在性[3]、可微性[4–5]、稳定性[6]、同变性[7]以及可析性[8]等取得一些进展。另一方面，早期关于此类方程的周期结果通常利用拓扑不动点定理与不定点指数方法得到的[9–11]。1974 年，Nussbaum[12]首次给出了依赖状态时滞微分方程的周期解存在性结果。对于一般的周期解存在性问题的结果，可参考文献[13]。2001 年，利用Mawhin 重合度定理并通过划分区域估计解的一致上界，Li 与Kuang[14]获得了如下方程的周期解

并给出自然且易验证的周期解存在性判定条件。从此以后，这个方法经常被用来处理时滞微分方程的周期解问题。另一方面，几乎周期函数是周期函数的自然推广[15–16]。时滞微分方程的几乎周期解存在问题成为数学研究者关注的主题。众所周知，带依赖状态时滞方程关于几乎周期解的研究还很少。

本文目的研究方程(1)的一般形式，即为其中x: R→Rn是未知函数，f与g在后文将具体给出。利用Schauder 不动点定理，本文分别给出方程(2)周期解与几乎周期解的存在性条件，这些判据是较易于验证的。同时，本文最后给出两个例子说明所得理论结果的可行性。

1 主要结果

定理1假使f(t,x,y)与g(t,z)关于t均为T-周期的，且分别满足Lipschitz 条件

其中Lf、Lg是Lipschitz 常数，对任意的(x1,y1),(x2,y2)∈Rn×Rn和z1,z2∈Rn。关于T-周期函数x，如果f(t,x(t),x(g(t,x(t))))满足

则方程(2)存在一个T-周期解。

证明 令X(T)为T-周期函数x:R→Rn的集合，它是赋予范数

的Banach 空间。定义如下T-周期函数x构成的有界集

显然，对x ∈XM，则有//x//C0≤MT。根据XM的定义，由于f(t,x,y)与g(t,z)分别满足式(3)和式(4)，且它们关于t均为T-周期的。所以，对任意的x ∈XM，式(5)成立。

接下来，证明方程(2)的T-周期解属于集合XM。定义映射G:XM →C0(R,Rn)为

因此，G不动点是T-周期解，并有

同时，利用式(6)，我们得到

所以，由式(5)与式(7)，得到

这就蕴含了Gx(t)∈X(T)。进一步地

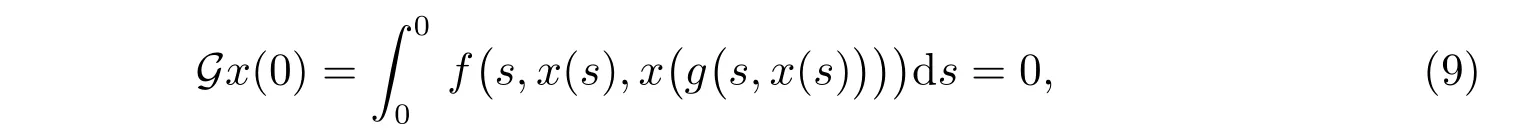
对任意的t,s ∈R，有

并且，对任意的s ∈R，有

故式(11)和式(12)，可得

这就说明了G是连续的。

由于XM是Banach 空间X(T)凸且紧子集，而G又是连续的，根据Schauder 不动点定理，我们可得G在x ∈XM存在不定点，该不动点也即是方程(2)的T-周期解。

为了证明方程(2)存在几乎周期解，我们首先给出一些基础定义和预备引理[15,17]。

定义1函数f是几乎周期的，是指若每个序列{α′n}存在一个子列{αn}，使得在R，式Tαf=limn→∞f(t+αn)一致成立。

令AP(R,Rn)代表从R 到Rn的几乎周期函数的全体，则(AP(R,Rn),//·//)是Banach 空间[16]。

引理1[15]若x:R→Rn是几乎周期的，则x(t)在R 上有界且一致连续的。

引理2[15]对x ∈Rn，若g:R×Rn →R 关于t是一致几乎周期的，且ϕ(t)⊂E是几乎周期的，其中E是Rn的紧子集，则g(t,ϕ(t))是几乎周期的。

引理3假如x: R→Rn是几乎周期的，g(t,x) : R×Rn →R 对x ∈H关于t是几乎周期的，其中H为Rn的闭子集，则x ◦(g(t,x(t)))是几乎周期的。

证明 由引理1 与引理2，几乎周期函数x(t)在R 上一致连续，且g(t,x(t))是几乎周期的。再由定义1，存在实序列α={αn}，使得成立

故x ◦(g(t,x(t)))是几乎周期的。

定理2若连续函数f(t,x,y)与g(t,z)关于t是几乎周期的，且分别满足Lipschitz 条件(3)和(4)。对几乎周期函数x如果f(t,x(t),x(g(t,x(t))))是一致有界的，则方程(2)存在一个几乎周期解。

证明 对几乎周期函数x，令N为f的界函数全体，即为

首先，证明方程(2)在集合XN中存在几乎周期解。定义映射H:XN →C0(R,Rn)为

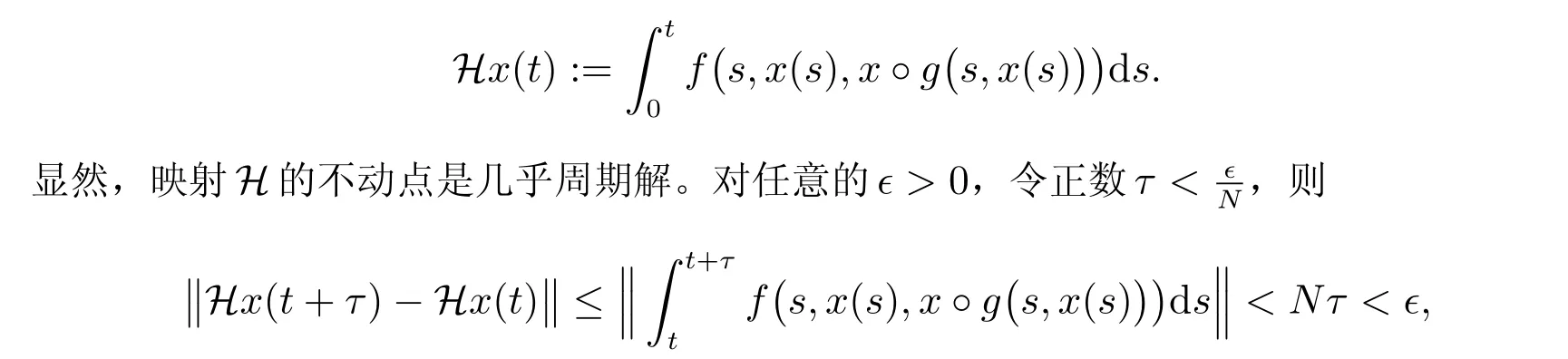
利用定理1 的证明方法，故有

显然有

对任意的t,s ∈R，可得

所以式(13)∼(15)蕴含H是自身到自身的算子。

现在证明算子H是连续的。对任意的ϵ>0 与xn(t)∈XN，它一致收敛于x(t)，存在正整数n1，当n>n1时，有

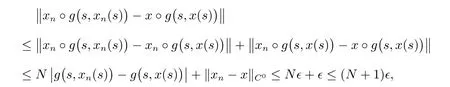
则

所以

这说明了H的连续性.

由于XN是Banach 空间AP(R,Rn)上的凸紧子集，且H是连续算子，根据Schauder 不动点定理，映射H存在一个不动点h ∈XN，它即是方程(2)的一个几乎周期解。

2 例子

本部分给出两个例子，例证所得上述结果的可行性。

例1考虑如下依赖状态时滞微分方程

由定理1，则方程(17)至少存在一个2π-周期x(t)解。

例2考虑如下泛函微分方程

易得Lf,Lg＜1 与//f//C0≤2。根据定理2 及例1 可得，方程(18)存在一个几乎周期解。

注1从上面两个例子可以看出，本文的主要结果是可行的，可作为依赖状态时滞微分方程存在周期解或几乎周期解的判据，这些结果改进了一些离散或分布时滞系统解的存在性结果。