地球变形近似解析解的构建及应用

周江存, 潘尔年, 孙和平,3, 徐建桥, 陈晓东, 崔小明

1 中国科学院精密测量科学与技术创新研究院， 大地测量与地球动力学国家重点实验室， 武汉 430077 2 台湾阳明交通大学， 灾害预防与水环境研究中心， 台湾新竹 300 3 中国科学院大学， 北京 100049

0 引言

地球在内力和外力作用下都会产生变形，尽管人们无法感知有些力源产生的变形，如日、月等天体的引潮力导致的潮汐变形(Melchior，1983)，但是安置在地表或卫星中的高精度大地测量观测仪器能够清楚地识别出这些信号(Sun et al.，2019).因此基于高精度观测的一些科学研究，如地球参考框架的建立与维持，需要扣除由于地球变形导致的干扰信号，如前述的固体潮信号，以及地表质量负荷、地震等(Altamimi et al.，2016).

描述地球变形的原理是基于无限小形变的假设，仅保留微小形变的一次项，而舍去高次项.通过数学手段建立的物理模型就包括三个基本方程：即(1)描述物质受力平衡的方程，对于静态的问题可以不考虑惯性项——位移对时间的二次导数；(2)描述弹性或非弹性介质应力应变状态的本构方程；(3)描述扰动位与扰动密度关系的泊松方程.将上述方程中的变量进行球谐展开后得到关于展开系数的一阶常微分方程组，其包含八个变量的八个常微分方程(可参考Alterman et al.，1959；Takeuchi and Saito，1972；郭俊义，2001；徐建桥和孙和平，2003；孙文科，2012).其中，水平位移和剪切应力又有球型和环型之分，因此这八个变量中分别有两个表示水平位移和剪切应力.

通常用勒夫数表示地球对力源的变形响应特征，它们分别对应着上述方程组中的位移和附加引力位的解.勒夫数是Love(1911)在研究地球的潮汐形变时定义的用来描述地球受引潮力作用而变形的两个无量纲的量，用h和k表示，分别描述对应于某球谐展开阶数的垂直位移与平衡潮潮高(引潮力位/地表重力)的比值和附加引力位与天体对地球引潮位的比值.后由Shida(志田)定义l描述水平位移与平衡潮水平分量的比值(Shida, 1912)，这三个数一般统称为勒夫数(其中l也称志田数).后来在研究地球受表面负载作用的变形也采用类似的三个无量纲的数，称为“负荷勒夫数”(Farrell，1972)；Saito(1978)定义了描述地球受地表剪切力而变形的“剪切勒夫数”.特别地，潘尔年和丁中一(1986)揭示了上述三组勒夫数之间的关系.此外，研究地球受点源位错(地震)作用而变形时也有类似的三个“位错勒夫数”(Sun and Okubo，1993).Okubo(1993)也揭示了地表位错勒夫数与震源处上述三组勒夫数之间的关系.Sun和Dong(2013)利用这种关系计算了地表位错勒夫数及浅源地震的位错勒夫数渐近值.

如果我们考虑一个SNREI(Spherically symmetric, Non-Rotating, Elastic and Isotropic，球对称、非自转、弹性各向同性)且包含自重的分层地球模型，那么地球变形的球型场和环型场是解耦的，所以由六个常微分方程共同描述了球型场的变形，由两个常微分方程共同描述了环型场的变形.再基于地球所受力源的性质所确定的边界条件，求解这个边值问题，地球的受力变形就可以在理论上模拟出来.由于环型场的问题只包含两个微分方程，因此求解相对比较简单，主要的难点体现在包含六个微分方程的球型场的解算中.

由于常微分方程的系数与地球的参数，如密度、重力、拉梅常数，以及球坐标系的矢径r有关，因此在计算上存在一些困难.当然，如果是一个简单的地球模型，如均匀球，求解就非常简单，这得益于Love(1911)从复杂的公式中发现了简洁的严格解析解这一伟大的工作，他给出的结果到现在仍得到广泛的应用(如Sun，2003，2004a，b；Takagi and Okubo，2017；Tang and Sun，2017).然而，对于一个分层的地球，没有严格意义上的解析解.Gilbert和Backus (1968)通过假设每层中重力是r的线性函数，其他参数是常数，得到了一组用球贝塞尔函数表示的解析解.然而，对于一个接近真实地球的地球模型来说，在地核中重力近似是r的线性函数，因此关于重力的假设在地核中是合理的，但是在地幔中重力不是r的线性函数，该假设是不合理的，其结果必然带来很大的误差.因此，一直以来数值计算方法仍是求解地球变形时常用的方法：如龙格-库塔数值积分法(如汪汉胜等，1996)、差分法(Poulsen，2009)、谱有限元方法(如Martinec，2000；廖彬彬等，2019).其中，四阶龙格-库塔方法是模拟SNREI地球形变最为广泛使用的方法.

在用龙格-库塔方法模拟计算中，第一个出现的困难是计算溢出的问题，这受限于计算机的数据表示及存储能力.这个问题从模拟海潮负荷形变时得到关注，因为涉及的常微分方程组是与球谐阶数相关的.不同于地球固体潮的研究只需要球谐展开的2阶和3阶的结果(Melchior，1983)，至多到4阶(Xi，1989)，海潮负荷需要至少数千阶的结果并结合渐近值以便采用Kummer变换(原理见下文)获得收敛的格林函数(Farrell，1972).因此为解决这个问题提出了许多方法，如Longman的无量纲化方法(Longman，1963).该方法使得各个变量的数值相差不是太大(如几个量级的差异)，计算更加稳定一些，但是这种方法只是让能够计算的最大球谐阶数提高一些而已.汪汉胜等(1996)注意到每个变量都包含一个rn因子(其中，n是球谐阶数)，提出了r幂因子法，即从每个变量中扣除rn因子.单纯采用r幂因子法，也不能彻底解决溢出的问题，需要在积分过程中的每一步进行归一化(如使所有变量的最大值为1).这实际上是每一步都从所有的变量中提取一个共同的常数，从而避免了溢出.鉴于所处理的微分方程组是线性的，所以可以通过地表的边界条件加以约束.实际上所有积分过程中提取的常数的乘积都被最后利用边界条件确定的未知常数吸收.因此，如果只计算地表的值，可以无需考虑这些提取的常数大小，然而如果要计算地球内部的形变，需要将这些提取的常数存储并代回.

解决了溢出问题，对于大部分问题来说，数值模拟都能够很好地开展.但是在模拟由地震引起的变形问题中，如果震源与场点(计算变形的点)距离比较近，那么所需要的球谐阶数n就非常高.Sun和Okubo(1993)给出了一个经验公式：所需计算的最大阶数为10a/d，其中a是地球半径，d是震源与场点的距离(r方向的投影).我们对此截断公式也进行了深入的研究，考虑到每个变量的不同渐近性质给出了新的截断公式(Zhou et al.，2019b).一般情况下，如果d=1 km，需要n=6万阶，如果要模拟地下爆炸对地表的变形影响，需要数十万阶.龙格-库塔方法对于高阶甚至超高阶的计算是无能为力的.当n很大时，从地心(实际计算中从中心均匀小球表面)开始，不管初始值如何设定，积分几步后几组独立解都变得线性相关，甚至一样.这会导致最后在地表确定未知系数时的矩阵产生奇异.我们发现这个情况的出现是因为六个变量不再独立(详见下文)，这是由地球变形的物理问题所决定的，属于内在的属性.只要采用六个常微分方程，这种情况就不可避免.这种情况在有限元方法中就不会出现，因为有限元方法仅仅以位移和附加位为变量，从而不存在变量相关的问题(廖彬彬等，2019).

计算中最重要的一点是效率问题，在龙格-库塔方法中，需要积分步长足够小以便每一层的各个物理量可以合理地假设为常数.我们对位错勒夫数的计算表明，积分步长不能超过100 m，否则球谐展开的高阶结果就会出错(Zhou et al.，2019a).这样就需要将地球分成非常多的层，导致计算速度非常慢.在有限元中，使用插值函数同样也需要节点之间的距离合适，对于球谐阶数较高的情形，最终的刚度矩阵也非常大，也会影响计算效率.实际上，有限元方法的优势主要体现在对三维地球模型的处理.

在地球变形的理论模拟中，如何使计算速度很快，又能够避免出现计算的溢出问题，并且当球谐阶数很高时也能轻松计算，这正是本文将要介绍的解析解方法结合DVP(Dual Variable and Position)传播矩阵法所具备的特征.

1 地球变形的解析解

由于环型变形求解非常简单，因此仅讨论球型变形.求解球型变形的常微分方程组为(Takeuchi and Saito,1972；Pan et al.，2015)

(1)

其中，UL、UM、φ、TL、TM、Q分别是垂向位移、水平位移、附加引力位、垂向正应力、垂向剪应力和引力位梯度(参考第三个等式)，r为球坐标系的径向分量，λ，μ是拉梅常数，ρ是密度，g是重力，n是球谐阶数.值得注意的是式(1)为齐次微分方程组，对于一个有内部力源的地球变形问题，微分方程组本来应该是非齐次的，但是如果我们假设力源是点源，那么可以将非齐次项转变成力源处的边界条件(参考Takeuchi and Saito，1972).因此只需要求解如式(1)的齐次方程组.

归根结底，求解微分方程组(1)的困难在于系数矩阵是变量，从而解不能简洁地表示出来.如果基于一些合理的假设，能够使得系数矩阵变成常数矩阵，那问题就非常简单了.解析解方法正是基于这样的思路，首先将地球分成若干层，然后对每一层作一些近似(Pan et al.，2015)：在液态地核的分层中假设密度为常数，重力是r的线性函数；在地幔和地壳的分层中，重力是常数而密度是r的反函数.此外，假设拉梅常数在每一层中为定值，并且定义一个新变量

ξ=ln(r/rj-1),rj-1≤r≤rj,

(2)

式中，rj和rj-1分别是第j层的上下边界.将新变量和上述的假设代入式(1)，我们就可以得到如下用矢量形式表示的微分方程.

dY/dξ=AY,

(3)

其中Y=(UL,UM,φ,rTL,rTM,rQ)T，最重要的是此时A为6×6的常数矩阵，因此方程(3)存在解析解，该解由系数矩阵A的特征值和特征向量表征，即

(4)

其中，所有的子矩阵都是3×3的，c1和c2是待定系数矢量，各包含3个未知数，

(5)

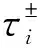
该方法的关键是对密度和重力在地球内部的分布作了假设，从而系数矩阵变成了常数矩阵.那么这些假设是否合理，是否会对结果产生很大的影响是我们首先需要回答的问题.通过与PREM(Preliminary Reference Earth Model，初步参考地球模型)(Dziewonski and Anderson, 1980)比较发现，由上述假设生成的模型与PREM模型的差异非常小，因此这种假设是合理的(Pan et al.，2015).实际上，上述的假设也是在充分考虑PREM模型的参数分布特性的基础上做出的.最重要的一点是：我们可以在顾及计算效率的情况下，减低层厚使得二者之间的差异更小.实际上只要层厚足够小，可以用任意的函数拟合模型参数且能够较好地控制误差.通过计算发现，模型的厚度可以设成数十公里(Pan et al.，2015；Chen et al.，2018；Zhou et al.，2019a).由此可见，这里的假设要比Gilbert和Backus(1968)合理得多.需要特别指出的是，如果层厚足够小，那么得到的结果就是真实的解，而非近似解.

尽管得到了理论上的解析解，但是对于PREM这样的地球模型，特征值和特征向量是不太可能有简单的解析形式或由普通函数直接表示出来.因此我们需要采用数值计算的方法计算特征值和特征向量，可以理解为是一种关于拉梅常数和球谐阶数的特殊函数.如同均匀球的解用球贝赛尔函数表示，虽然球贝赛尔函数是解析的，但仍然需要采用递推公式及适当的技巧以便能够准确地将它数值地计算出来.

然而，直接利用式(4)并采用普通的传播矩阵方法，在球谐阶数很高的时候，也会导致数值计算的溢出(Pan et al.，2015).因此，我们介绍一种新的传播矩阵方法，称为DVP方法(Pan，2019；Zhou et al.，2019a)，使得传播稳定而高效.

2 DVP传播矩阵法

普通传播矩阵法溢出的原因是：当球谐阶数很高时(如n=10000)，矩阵的6个特征值接近于n+1、n、n-1、-n、-(n+1)、-(n+2)，其中，如式(5)所示，对于正的特征值，指数eτ ξ就会是一个更大的数，超出了计算机的存储能力，从而导致向上溢出.虽然可以把层厚取得足够小(ξ很小)，从而某一层内不会溢出，但是传播数层之后，溢出还是会出现.DVP传播矩阵法就是避免在传播过程中直接使用含有大的正实部的特征值参与计算，原理如下：

首先将式(4)改成

(6)

其中ξj即ln(rj/rj-1)为j层的上边界的值.实际上这种改变是从c1中提取了某一个常数，我们用c3表示新的待定常数.显然有如下的关系：

〈-s1ξj〉c3=c1.

(7)

在某种程度上，这种改变类似于龙格-库塔方法每一步积分过程中实施的归一化.为了方便，定义

(8)

式中，我们用n对变量进行了规格化使得每个变量具有相同的量级，这只是使矩阵A稍作改变而已，从而特征向量也作相应调整.但这并不影响问题的本质(特征值不变)以及我们对方法的描述.这样一来，在第j层的上边界(ξ=ξj)和下边界(ξ=0)，分别有

(9a)

和

(9b)

其中E为3×3的单位阵，上标u和l表示上边界和下边界.通过将上面的(9a)和(9b)两式写成4个由子矩阵表示的等式，调整变量顺序，并消去系数后再表示成矩阵形式，有

(10)

其中

(11)

需要注意式(10)中上下边界处变量的位置，普通的传播矩阵法的形式为(Pan et al.，2015)

(12)

式中，传播矩阵P′的具体形式可以很容易从式(4)或(9)导出，刚度矩阵法的形式为(Chen et al.，2018)

(13)

式中，传播矩阵P″也可以很容易从式(9)导出.可以看出式(10)，(12)和(13)三种方法中上下边界处变量的位置是明显不同的，而正是这种简单的位置调换产生了不一样的计算效果.

从式(11)可以看出，虽然s1包含具有正实部的特征值，但是前面有一个负号，因此避免了大数的产生，从而防止了溢出.特别地，当n非常大时，可以得到

(14)

因此

(15)

这说明，当球谐阶数很大时，U和T是相关的，这也是为什么龙格-库塔方法无法计算高阶解的原因.然而这种相关性可以使我们能够直接求得位错勒夫数在震源处的值，从而求出当n很大时候的位错勒夫数渐近值，并可实施Kummer变换获得收敛的位错格林函数(Zhou et al.，2021).此外，我们还发现，

(16)

其中a是地球半径.也就是说，对于地表负荷这类在地表有非零值边界条件的问题来说，地表的位移和附加引力位可直接由最上层的特征向量求出，而不管地球内部的结构如何，这也解释了为什么高阶负荷勒夫数只与地壳最外层结构有关.这实际上也是求当n很大时负荷勒夫数渐近值的新方法(见周江存和潘尔年，2021).

有了相邻两层的传播矩阵，就可以将解进行传播，j层和j+1层之间的传播矩阵为

(17)

其中

(18)

重复迭代公式(18)，就可以得到初始层和目标层之间的传播矩阵，从而得到两个界面上的解之间的关系，由边界条件即可求得最终的解(Zhou et al.，2019a).

3 爆炸源格林函数

不同的勒夫数是构建不同格林函数以及计算相应力源引起的地面和内部变形导致的位移场、重力场和应变应力场变化的基础(Pan，2019).需要指出的是，我们定义的位错勒夫数与以往如Sun和Okubo(1993)略有不同，采用了不同的规格化(详情可参考Zhou et al.，2019a)，新定义有助于我们直观地发现它们的渐近性质，即随着n的增加，它们具有怎样的变化特征，从而为能够拟合出渐近值给出直观的感知，为能够实施Kummer变换从而加速格林函数的收敛创造了条件(Zhou et al.，2019b).此外，我们最近也提出了另一种方法获得位错勒夫数渐近值，即根据传播矩阵的特点直接求解位错勒夫数的渐近值(Zhou et al.，2021).渐近值的成功计算为我们能够模拟浅源爆炸引起的地表形变奠定了基础.对于像浅断层或浅源爆炸的情形，我们再无需叠加像上文提及的数十万那么高阶的位错勒夫数，只需实施Kummer变换叠加少量低阶的位错勒夫数即可.

格林函数涉及球函数的求和，其系数就是勒夫数或其组合.对于球对称的地球模型，任意的断层都可以表示成四种独立的断层模式的组合(Sun and Okubo，1993；Zhou et al.，2019a)，它们是垂直走滑、垂直倾滑、水平拉张和垂直拉张，分别用两个数字组合表示，即分别为12，32，22，和33.爆炸源的矩张量可以表示为(Kumagai et al.，2014)

M0=3KsΔVc=(3λs+2μs)ΔVc,

(19)

其中，K表示体膨胀系数，下标s表示震源处的值，ΔVc是由任一个正交的拉张断裂(11，22或33，由于对称性，11可通过22的旋转获得)产生的无应力体积变化(Aki and Richards，2002).因此爆炸源的格林函数就可用位错格林函数表示为(也可参考孙文科，2012)

(20)

其中，(r,θ,φ)构成球坐标系，

(21)

(22)

其中，a1、b1、c1和d1均为常数，可由高阶位错勒夫数拟合而得(Zhou et al.，2019b)，或根据分层地球模型的参数直接计算出来(Zhou et al.，2021).(22)式中的两个等式右端的第一个求和部分比(21)式要收敛得快得多，因此可截断到nMax，而第二个求和具有严格的解析表达式(参考Zhou et al.，2020；Tang and Sun，2021).

4 数值结果与讨论

我们以地下100 m、200 m和500 m深处的爆炸为例，模拟爆炸产生的永久变形.首先计算对应不同震源深度的地表位错勒夫数.采用解析解的方法避免了传统的龙格-库塔方法中的变量相关问题，可以很容易地计算超高阶的位错勒夫数.图1和图2分别显示了震源深度为100 m时的球谐阶数n从0到107阶的位错勒夫数h和nl的计算结果.由于我们考虑的问题只涉及两个独立的拉张型位错模式，所以图中只给出这两个位错模式的结果.

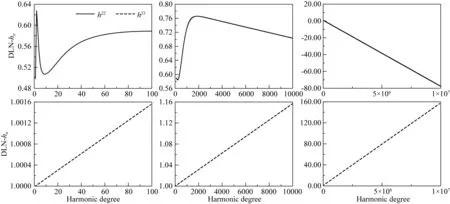
图1 地表位错勒夫数hn(震源深度100 m. 左侧两图是0～100阶的结果，中间两图是100～104阶的结果，右侧两图是104～107阶的结果)Fig.1 Dislocation Love number hn on the Earth′s surface for source depth at 100 m (the left two plates are for degrees 0～100, the middle two plates are for degrees 100～104 and the right two plates are for degrees 104～107)

图2 地表位错勒夫数ln (震源深度100 m. 左侧两图是0～100阶的结果，中间两图是100～104阶的结果，右侧两图是104～107阶的结果)Fig.2 Dislocation Love number ln on the Earth′s surface for source depth at 100 m (the left two plates are for degrees 0～100, the middle two plates are for degrees 100～104 and the right two plates are for degrees 104～107)

从图中也可以很容易地看出位错勒夫数的渐近特征，两种位错勒夫数在高阶表现出与n呈线性的关系，这在垂直拉张的结果中更加明显，从低阶的结果中就开始显现，其变化看上去就是一条直线.通过这种渐近特征我们可以拟合出位错勒夫数渐近值的线性表达式，其表达式的系数列于表1中，这些系数对我们能够使用Kummer变换加速位错格林函数的收敛至关重要.从表中可看出，这些系数的线性项具有明显的特点，h和nl的线性系数大小相等，符号相反；垂直拉张位错勒夫数的线性系数正好是水平拉张结果的-2倍.

表1 位错勒夫数渐近值Table 1 Asymptotic dislocation Love numbers

图3和图4分别给出了不同深度处的无应力单位体积(即假定M0=3K)爆炸源垂直位移和水平位移的格林函数.不同于地震断层需要分成若干的子断层，每个子断层认为是点源，再叠加所有子断层对位移的贡献，爆炸源本身就是一个点源事件，所以从其格林函数中就可看出其对位移场的影响大小.并且位移场是以爆炸源与地心连线为轴旋转对称的，即位移场只与球面角距离有关，而与方位无关.

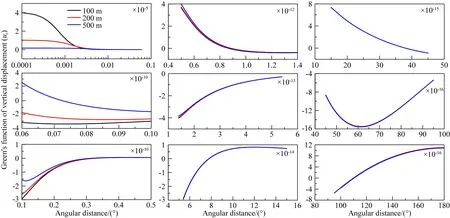
图3 地下不同深度处无应力单位体积爆炸源引起的地表垂直位移(单位：m)Fig.3 Vertical displacements (unit: m) on the Earth′s surface due to underground explosions of unit stress-free volume at different depths

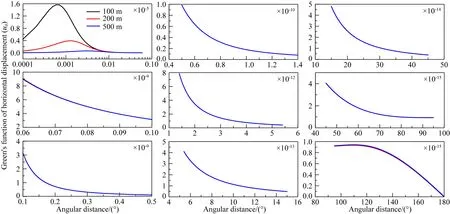
图4 地下不同深度处无应力单位体积爆炸源引起的地表水平位移(单位：m)Fig.4 Horizontal displacements (unit: m) on the Earth′s surface due to underground explosions of unit stress-free volume at different depths

为了显示爆炸源引起的全球变化特征，我们将角距离分成不同的区域以显示位移场变化的详细特征.为了显示方便，在每个区域都从格林函数中提取出一个因子，标注在图中的右上角.尽管对于爆炸源来说，远场的位移是非常小的，这里将远场的结果也显示出来是为了(1)保持格林函数的完整性；(2)显示格林函数的收敛性以说明位错勒夫数渐近值在格林函数计算中的重要性.从图中可以看出，随着深度的增加，地表的变形会逐渐减小，显著的位移场只发生在离爆心大约100～200 m的范围之内，垂直位移的幅度在6 km之外降低5个数量级，水平位移的幅度在6 km之外降低4个数量级，在50 km之外降低5个数量级.因此，如果爆炸当量比较小，那么显著的永久形变只会发生在离爆炸中心不远的地方.当然，这个距离会随着爆炸当量的增大而增大，同时也随着爆炸源深度的减小而增大.

5 结论

我们介绍了一种计算地球受力变形勒夫数的解析解方法.该方法通过合理假设地球内部结构参数，使得变系数的常微分方程组变成常系数的常微分方程组，从而其解可以用系数矩阵的特征值和特征向量解析地表达出来.

通过引入一种特殊的DVP传播矩阵方法，解决了计算的溢出和球谐展开高阶项的变量相关问题，从而可以稳定和高效地计算出超高阶的位错勒夫数，并且利用该方法可直接求得震源处的位错勒夫数渐近值，从而确定任意位置的位错勒夫数渐近值.特别地，从计算得到的勒夫数随阶数的变化中能够很直观地发现它的渐近特征，从而拟合出渐近值.采用Kummer变化加速了位错格林函数的收敛，由此计算了浅源爆炸的格林函数.

我们模拟分析了浅源爆炸产生的地球表面的永久形变特征.结果表明，采用解析解方法结合DVP传播矩阵方法可以解决位错勒夫数和格林函数的计算问题.最后需要说明的是，本文的数值结果是基于静态的变形理论，未考虑爆炸产生的波及其引起的破坏性变形.

致谢特别感谢我们前期系列工作的合作者美国俄亥俄州立大学Michael Bevis教授.