共振条件下竖直悬臂输流管的局部分岔分析

张嘉文，高晓凌，谢沅泽，卞小霞

（1.盐城工学院 信息工程学院，江苏 盐城 224051；2.盐城工学院 土木工程学院，江苏 盐城 224051；3.盐城工学院 数理学院，江苏 盐城 224051）

管道系统是一种重要的载流装置，在石油化工行业、核工业工程和航空航天工程等领域有广泛的应用。由于管道系统在工作过程中受外界激励的影响，其中的流体产生非定常流动，引起管道系统的流-固耦合非线性效应，导致输流管系统失稳，严重时发生爆裂，继而引发灾难性的事故。因此，管道系统的非线性动力学特性研究受到了广大学者的重视。

1 输流管道系统的研究现状

输流管道系统是非线性系统，需要用非线性动力学分析方法研究[1]。Hosseini 等[2]基于Euler-Bernoulli 梁模型，利用修正的应变梯度理论研究了长度尺度参数、外径和长径比对固有频率和颤振临界速度的影响。金基铎等[3]研究了悬臂输流管道受弹性支承和运动约束作用的稳定性和分岔现象。Mao 等[4]分析了输流管在3∶1 内共振下的受迫振动响应。Wang 等[5]得到了松散约束中的不同参数对悬臂梁非线性动力学行为的影响。方孟孟等[6]基于Galerkin 法研究了悬臂输流管系统在基础激励与脉冲内流联合作用下的动力学行为。张宇飞等[7-8]分析了输送脉动流体的悬臂管道在谐波外力作用下的非线性共振响应、模态相互作用及倍周期和混沌振动，并且通过实验的方法对基础激励作用下悬臂输流管的动力学行为进行振动测试分析。

本文以悬臂输流管的非线性动力学系统为讨论对象，分析平衡点处稳定条件不满足时分岔的情况。讨论了2 类临界特征根的情况。分别是2 个零特征值，1 个零特征根和1 对纯虚特征根的情况，给出了不同情况下的转迁曲线及平衡解稳定区域。

2 动力学模型

张宇飞等在文献[7]中得到了受外激励及内共振影响的输流管系统非线性无量纲系统如下

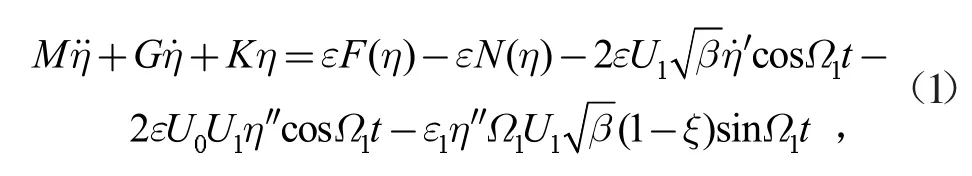
式中：“·”表示对时间t 的偏导数，“′”表示对X 的偏导数各项表达式及系数都可以在文献[7]中找到。张宇飞等应用摄动分析法及Galerkin 离散法得到平均方程如下

式中：X=[x1，x2，x3，x4]，式（2）中各系数均可在文献[7]中找到。共振关系为

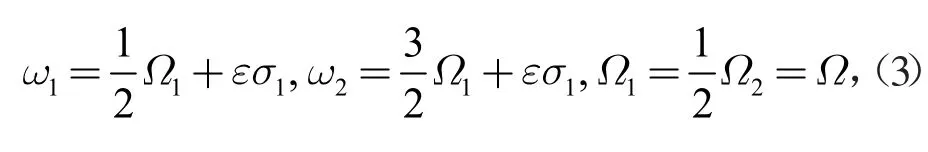
式中：σ1和σ2是2 个调谐参数。

式（2）在平衡点（x1，x2，x3，x4）=（0，0，0，0）处的Jacobian 矩阵为

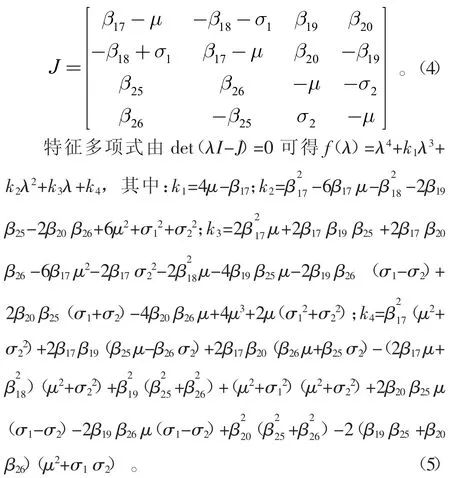
由Hurwitz 判据，系统在原点处稳定，当且仅当下列条件成立

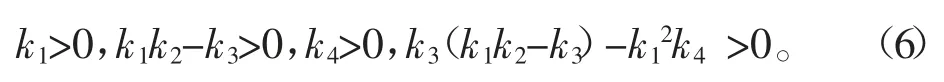
条件中不等式同时成立时，矩阵的特征根实部均为负数，否则，若是有1 个不等式不成立，则平衡点不稳定，可能发生分岔。

3 局部分岔分析

下面讨论系统在原点附近受参数（δ1，δ2）扰动后的动力学行为，分析特征根为1 个零和1 对纯虚数的情况。

选取参数值如下

此时，雅可比矩阵的特征值为λ1=0，λ2，3=±3i，λ4=-2，参数β17，μ 被扰动，变换为：β17=-1+δ1，μ=0+δ2，状态变量经如下变换

式中：Nfi（i=1…4）见附录。系统在初始平衡点（y1，y2，y3，y4）=（0，0，0，0）处，参数为零时Jacobian 矩阵为

接下来讨论式（11）的平衡点及稳定性。式（11）的Jacobian 矩阵为

式（11）的平衡点有如下情况：①z=r=0 为初始平衡点；②z2=-δ1/4，r=0 为静态分岔解次Hopf 分岔解二次Hopf 分岔解。

以上平衡解的稳定性条件由Jacobian 矩阵（12）分析得到，对于初始平衡解①，δ1＞0，δ2＞0 时平衡点稳定。记其稳定边界即转迁曲线为L1：δ2＝0（δ1＞0），L2：δ1＝0（δ2＞0）；对于静态分岔解②，δ1＜0 时解存在，δ1＜0 且δ1/4+δ2＞0 时解稳定，则有稳定边界L2：δ1＝0（δ2＞0），L3：δ1/4+δ2=0（δ2＞0）；对于一次Hopf 分岔解③，δ2＜0 时解存在，稳定条件为δ2＞0，5δ1＋39δ2＞0，对比得到此解无法稳定，转迁曲线是L4：5δ1＋39δ2＝0（δ1＞0）；对于二次Hopf 分岔解④，δ1＋4δ2＜0，5δ1＋39δ2＞0 时解存在，50δ1+352δ2＞0 时解稳定，得到稳定边界为L3：δ1/4+δ2=0（δ2＞0），L5：50δ1+352δ2＞0。

由上述分析可知系统平衡解的转迁曲线及稳定区域如图1 所示，初始平衡解①稳定性区域为I，参数穿过L2分岔出静态分岔解②，解②的稳定性区域为Ⅱ，参数经过L3时分岔出二次Hopf 分岔解④，区域Ⅲ中，解②不再稳定，解④稳定。

从图1 的不同区域选取参数（δ1，δ2）验证理论分析的结果。图2（a）、2（b）、2（c）是不同参数及不同初始状态对应的状态变量x1的时间历程曲线，图2（d）是二次Hopf分岔解对应的相轨线在（x1，x2）平面上的投影。首先从平衡解（z，r）＝（0，0）的稳定区域Ⅰ中选取（δ1，δ2）=（0.1，0.1），初始状态为（x1，x2，x3，x4）=（-0.1，0.1，0.1，0.1），如图2（a）所示，轨线最终收敛到零点；其次，从静态分岔解（z，r）=（－δ1/4，0）的稳定区域Ⅱ中选取（δ1，δ2）=（-0.1，0.2），初始条件取为（x1，x2，x3，x4）=（0.1，0.1，-0.1，0.1），由图2（b）可见轨线收敛到确定的非零解；最后，从二次Hopf 分岔解的稳定区域Ⅲ中选取（δ1，δ2）=（-0.1，0.018），初始条件取为（x1，x2，x3，x4）=（-0.1，0.1，0.1，0.1），由图2（c）、2（d）可见状态变量作稳定的周期运动，相轨线收敛到稳定的极限环。

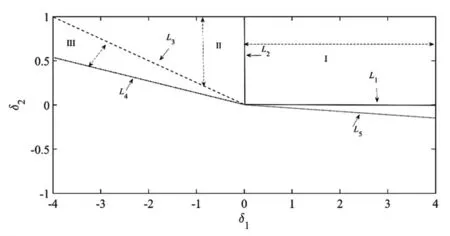
图1 系统关于参数（δ1，δ2）的转迁曲线图

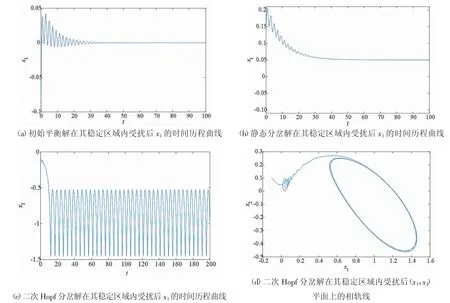
图2 不同条件下时间历程曲线及相轨线

4 结论

通过Hurwitz 判据分析了平衡点的稳定性条件。对于特征值为1 个零和1 对纯虚根的临界情况，分析了平衡条件不满足时，系统的局部分岔行为。参数（μ，β17）受扰后，系统可能会产生4 个平衡解：①z＝r=0；②z2=-（δ1＋4δ2）。其中第三类存在性与稳定性条件冲突，无法实际产生，其他3 个解在相应的稳定区域均可产生，数值分析验证了理论结果。