基于Lewis和Liu定理的Ramanujan-Selberg连分数及其倒数的2-剖分

李紫微

(重庆师范大学 数学科学学院，重庆 401331)

拉马努金(Srinivasa Ramanujan)是一位著名的数论家，其研究的内容颇为丰富，在椭圆函数、超级几何函数、整数拆分、级数等领域都做出了重大贡献。其中大部分研究都起源于Theta函数和q级数，Theta函数是椭圆函数理论的基本组成部分，Ramanujan独立发展了他自己的椭圆函数理论。这些研究成果都出自于Ramanujan遗失的笔记本。

连分数是Ramanujan遗失笔记本中重要的内容之一，其研究方向颇多，比如连分数的收敛与发散、模方程、同余等式、剖分等。其中，连分数的剖分是人们最近研究的热门方向。经过多年的发展，人们也得到了许多连分数的研究成果，其中主要研究的Ramanujan连分数有Rogers-Ramanujan连分数[1]

Ramanujan立方连分数[2]

Ramanujan-Gollnitz-Gordon连分数[3]

Ramanujan-Selberg连分数[4-5]

关于它们的剖分是近年来研究的热点。剖分是指将一个幂级数根据幂的模n剩余类展开。目前连分数剖分的主要研究手段为：Jacobi三重乘积恒等式、Jacobi五重乘积恒等式、theta函数的线性组合以及Lewis和Liu恒等式相关定理[6]。其中某些剖分等式对数学的其他方向也有重要的作用。例如，Z Cao[7]利用生成函数(q;q)∞(q2;q2)∞的3-剖分证明了Chan的同余等式

同余等式与连分数又有密切的联系,Chan[8]用Ramanujan立方连分数的两个结果也证明了上式。Ramanujan[9]用Rogers连分数的两个等式证明了下面的等式

这里p(n)是分拆函数，该式被Hardy称为Ramanujan“最漂亮的等式”，因此连分数的剖分具有一定的研究意义。

2010年，Vasuki,Bhaskar和Sharath用无穷乘积得到了Ramanujan-Selberg 连分数倒数的4-剖分[10]

除此之外，可以利用Jacobi三重乘积恒等式得到Ramanujan-Selberg连分数倒数的2-剖分[11]

在本篇文章中，将利用Lewis和Liu恒等式等相关定理得到Ramanujan-Selberg连分数及其倒数的2-剖分的不同的形式。

1 预备知识

为了叙述方便，对符号的约定如下：S(q)表示的是Ramanujan-Selberg连分数；S(q)-1表示的是Ramanujan-Selberg连分数的倒数；C表示全体复数；N表示正整数。

有关Ramanujan连分数剖分的证明比较复杂且会用到许多相关定义以及定理，这章内容会简单介绍。

定义1[11]设任意的z,q∈C,定义q为无穷移位阶乘

(1)

(z1,z2,…zn;q)∞:=(z1;q)∞(z2;q)∞…(zn;q)∞，

(2)

令N0=N∪{0}，于是当z,q∈C，q≠0且|q|<1时，所有的无穷乘积都是收敛的，然后由定义可以得到以下等式:

(z;q)∞=(z,zq;q2)∞;

(3)

(z2;q2)∞=(z;q)∞(-z;q)∞.

(4)

定义2[6]设任意的z,q∈C,当q≠0且|q|<1时，有以下定义：

[z;q]∞:=(z;q)∞(z-1q;q)∞，

(5)

[z1,z2,…zn;q]∞:=[z1;q]∞[z2;q]∞…[zn;q]∞，

(6)

其中zn≠0(n=1,2,3,…)。

则由定义1和定义2我们可以得到下面相关等式：

[z-1;q]∞=-z-1[z;q]∞=[zq;q]∞，

(7)

[z;q]∞=[z,zq;q2]∞，

(8)

[z,-z;q]∞=[z2;q2]∞，

(9)

[z-1q;q]∞=[z;q]∞，

(10)

以及

[-1;q]∞[q;q2]∞=2.

(11)

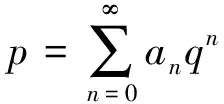
引理1[6]设a1,a2,…an;b1,b2,…bn∈C|0|满足

(1)当ai≠qnaj，i≠j时，对任意的n∈Z(整数)；

(2)当a1a2…an=b1b2…bn时，我们则有

(12)

2 主要结果及证明

Ramanujan-Selberg连分数及其倒数的2-剖分的证明过程

定理1设任意的复数q，当q≠0且|q|<1时，则S(q)的2-剖分为

(13)

证明

Ramanujan-Selberg连分数展开成幂级数为[4-5]

(14)

由等式(3)可知

(q;q2)∞=(q,q3;q4)∞,

(15)

又由等式(5)可以得到

(q;q2)∞=(q,q3;q4)∞=[q;q4]∞,

(16)

(q2,q2;q4)∞=[q2;q4]∞,

(17)

根据等式(8)(16)(17)得到

[q;q4]∞=[q,q5;q8]∞,

(18)

[q2;q4]∞=[q2,q6;q8]∞,

(19)

所以，结合上述由等式(14)可知

(20)

接着，我们令

S(q)=a(q2)+qb(q2),

则得到

(21)

再由等式(9)(21)得到

(22)

其中结合等式(8)可以得到

(23)

然后结合等式(22)(23)(9)，我们得到

(24)

然后利用等式(10)，可以得到

(25)

接着在引理1中，用q16代替q且取n=3为

于是得到

(26)

然后设(a1,a2,a3;b1,b2，b3)=(1，-1，-q15;q3,q5,q7)代入上面的等式得到

(27)

利用等式(7)可以得到

[-q-8;q16]∞=q-8[-q8;q16]∞,

[-q-10;q16]∞=q-10[-q10;q16]∞,

[-q-12;q16]∞=q-12[-q12;q16]∞,

[-q-15;q16]∞=q-15[-q15;q16]∞,

[q-15;q16]∞=-q-15[q15;q16]∞,

则结合等式(27)可以得到

(28)

又可以利用等式(9)(10)(11)，我们得到

(29)

最后结合等式(25)(29)可以得到a(q2)表示为

a(q2)=

再次利用等式(8)(9)(10)得到

(30)

同等式(21)同理可得

(31)

然后我们利用引理1，继续用q16代替等式(12)中的q，令

(a1,a2,a3;b1,b2，b3)=(1，-1，-q;q5,q9,q-13),

将其代入等式(31)可得

(32)

接着利用等式(7)可得

[q-13;q16]∞=-q-13[q13;q16]∞,

[-q-13;q16]∞=q-13[-q13;q16]∞,

[-q-14;q16]∞=q-14[-q14;q16]∞,

[-q-1;q16]∞=q-1[-q;q16]∞,

[q-1;q16]∞=-q-1[q;q16]∞,

将上面五个等式代入(32)可得

接着同等式(28)的证明相同，可以得到

(33)

最后将等式(33)代入等式(31)中可得

(34)

所以，通过等式(30)(34)，得到了连分数S(q)的2-剖分为

于是，我们证明了定理1。

定理2设任意的复数q，当q≠0且|q|<1时，S(q)-1的2-剖分为

(35)

证明

首先得到连分数S(q)的倒数为

然后，我们令

S(q)-1=c(q2)+qd(q2),

于是我们结合等式(9)(10)得到

(36)

再利用等式(8)可得

接着代入等式(36)以及结合等式(9)(10)可得

(37)

然后我们利用引理1，用q16代替等式(12)中的q，令

(a1,a2,a3;b1,b2，b3)=(1,-1,-q15;q3,q5,q7),

将其代入等式(26)得到

通过上面的等式，同等式(27)的证明一样，得到等式(29)，然后将等式(29)代入到等式(37)中得到c(q2)的值为

c(q2)=

(38)

同等式(36)同理可得

(39)

利用引理1，用q16代替等式(12)中的q，令

(a1,a2,a3;b1,b2，b3)=(1,-1,q;-q3,-q9,-q-11),

接着将其代入等式(26)中得到

(40)

然后利用等式(7)可得

[-q-11;q16]∞=q-11[-q11;q16]∞,

[q-11;q16]∞=-q-11[q11;q16]∞,

[-q-12;q16]∞=q-12[-q12;q16]∞,

[-q-1;q16]∞=q-1[-q;q16]∞,

[q-1;q16]∞=-q-1[q;q16]∞,

将上述五个等式代入等式(40)中可得

(41)

最后将等式(41)代入等式(39)中可以得到d(q2)的值为

(42)

于是通过等式(38)和(42)，我们得到了连分数S(q)-1的2-剖分为

即证得定理2。

3 结语

在已有Ramanujan-Selberg连分数剖分的研究成果上，本文采用了新的方法推出了该连分数2-剖分的不同形式,除此之外，可以在以后的研究中，基于2-剖分的成果继续得出Ramanujan-Selberg连分数的3-剖分和4-剖分。