复合材料捻子条区三角网格划分
王世杰
(上海飞机制造有限公司,上海 201324)
0 引言
碳纤维增强树脂基复合材料具有高比强、高比模量、抗疲劳、耐腐蚀、可设计性强等特点,因而广泛应用于航空航天领域,并带来明显的减重效益。随着人们对飞机整体重量的重视,复合材料已越来越多的应用在尾翼、机身、机翼等主承力结构中。其中T 型、工型以及帽型结构是复合材料加筋壁板结构的典型构件。对于工型长桁结构一般是由上盖板、下底板、左/右C 型构件组合而成的,左/右C 型构件在与上盖板、下底板组合时,会产生三角空隙区。图1 是工型长桁截面示意图。在实际制作中,一般使用一定体积的复合材料填充物(捻子条)来填充三角空隙,以降低应力集中并提高R 区成型质量。图2 是捻子条形状示意图。
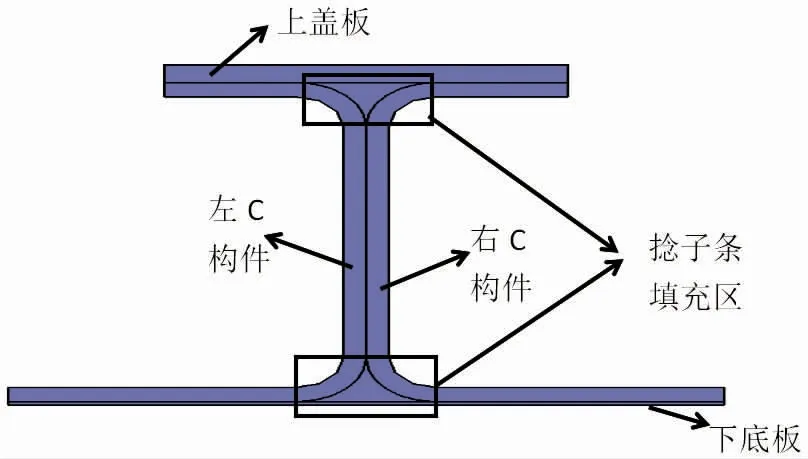
图1 工型长桁截面示意图
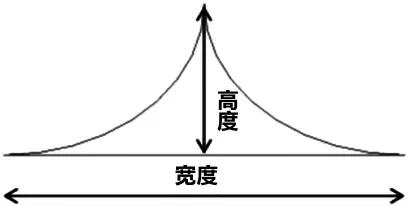
图2 捻子条形状示意图
复杂结构在划分网格时,由于形式复杂而计算花费时间长,或者由于计算机内存不足时,往往对结构进行几何简化。但为了得到准确的分析结果,结构几何简化模型也应尽量靠近原始模型,简化一些尺寸相对较小的细节,主要的结构几何形状一定要保留,随意的删减一些结构,会改变模型的刚度,得到的结果与实际值之间存在巨大的差别。T 型/工型等梁或长桁结构在划分网格时,若对捻子条区域几何简化,则腹板与缘条相交处呈直角,几何形状剧烈变化导致该处应力集中,使仿真分析结果失真。图3 是将捻子条区几何简化后应力仿真分析结果。从图3 中可以看出直角处应力值明显高于其他区域。故T 型、工型以及帽型加筋壁板的三角填充区不能几何简化,需要对捻子条区域进行仿真细节建模,以得到较为准确的仿真结果。
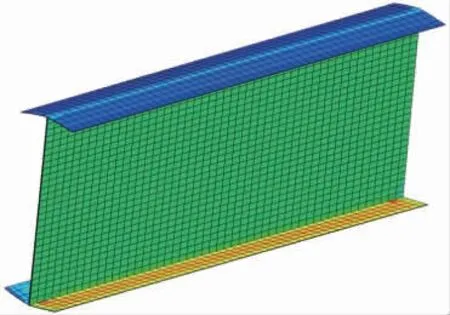
图3 捻子条区几何简化后应力仿真分析结果
在复合材料仿真细节建模过程中,如何高效、快速划分网格,是仿真分析过程中亟待解决的问题。有限元的前处理工作长期停留在手工操作阶段,不但费时费力,而且容易出错。随着计算机技术、编程技术的迅猛发展,以及人们对仿真建模效率要求的不断提升,人们越来越重视网格自动生成算法的研究。相关学者已提出了多种自动程序的有限元网格生成算法。这些算法对任意复杂形状区域的网格剖分鲁棒性强,能尽可能地避免病态三角网格的出现。这些算法多是采用C、C++或C#等语言编制,或者基于这些语言的程序库,算法复杂度大,约束条件多。目前复合材料建模多采用Abaqus 软件,该软件的二次开发脚本使用经达索系统定制的Python 语言。若想利用已有算法实现捻子条区域的三角网格剖分,需用Python 语言重新编写。
本文以Delaunay 三角网格划分规范为基础,利用捻条三角填充区近似对称性的几何特点,使用Abaqus的内核脚本语言Python,重点开展工型/T 型等梁、长桁以及帽型加筋壁板等复材结构的三角填充区域的网格自动划分研究,探索和验证网格自动划分算法的可行性和可靠性。使用该算法划分的三角网格质量高,算法实现简单,为后续工型/T 型等结构的复材零件快速建模发挥了重要作用。
1 网格划分基本思想
杨辉三角,又称帕斯卡三角,它是一个无限对称的数字金字塔,从顶部的1 开始,下面一行中的每个数字都是上面两个数字之和。图4 是杨辉三角形。从图中可以看出,如果将上一行的数字与下一行紧邻的两个数字用直线顺序相连,将构成一个完美的等边三角形。
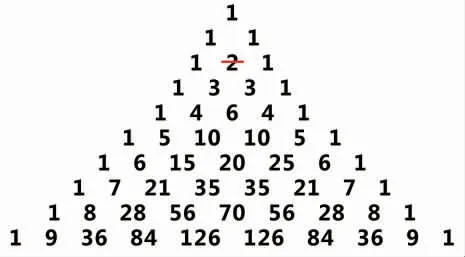
图4 杨辉三角形
针对某一区域的三角剖分问题,是指对有限平面(空间)点集内的点,按一定的方式连接起来,成为互不交叉三角形网,通常情况要求划分出的三角形网格应尽量均匀,即避免出现狭长的三角形。有限元网格生成技术的方法很多,但俄国数学家Delaunay 在1943 年证明:必定存在且仅存在一种剖分算法,能够满足“最大最小角”优化准则。即所有三角形的最小内角之和最大,通常称之为Delaunay 三角剖分。Delaunay 网格划分规范广泛应用于有限元网格自动生成中,确保了网格中的三角形形状处于可控状态。
Delaunay 三角剖分算法保证了任意空间区域用三角形剖分的可靠性。但Delaunay 算法较为复杂,需要同时满足多个附加条件。捻子条区域截面是曲边三角形的异形截面,且具有对称性。基于捻子条区域形状特点,本文在Delaunay 算法规则的基础上,采用杨辉三角模型的三角网格剖分方法,具有算法实现难度低、网格结构形式简单等特点。
2 网格质量判定标准
网格质量是决定计算效率和计算精度的重要因素。很多情况在模拟计算过程中,系统会发出单元质量不合格的警告信息,严重时会导致出错进而导致计算中断。因此,建立网格质量判定标准体系,对于仿真分析具有重要的意义。
Abaqus 软件针对二维三角形单元的主要质量指标包括两种:
(1)单元的形状因子表示单元的面积与该单元具有相同的外接圆半径的等边三角形的面积之比,形状因子的取值范围为0~1,值越大表明该单元的形状越好。
(2)三角形单元纵横比为各边长度与三角形各个边上的高度的比值再乘以√3/2,如果比率小于1,则取倒数。取其中最大值作为单元的纵横比。单元的形状越不接近等边三角形,纵横比越大。纵横比理想值等于1,通常该值不能超过8。
3 捻子条区域的曲边三角形网格剖分算法
输入:按顺序输入捻子条曲边三角形各曲边的节点编号,节点坐标。
输出:捻子条区域的三角网格。
假定已经由其他自动化程序或手工完成了捻子条区域的曲边三角形边界点的定义,即确定了曲边三角形各曲边的节点编号顺序以及相应的坐标值。本文采用的三角剖分算法如下:
(1)按照一定的顺序依次读入曲边三角形的节点编号、节点坐标。令曲边三角形曲边相交的顶点编号为0,向下依次编码为1,2,3……
(2)在曲边三角形的左曲边与右曲边对应节点之间,按照杨辉三角结构形式布置等分节点;
(3)从编号为2 的节点开始,记录该行及上一行(包括曲边上的节点和等分节点)节点编号、节点坐标。计算每个顶点内角的大小余弦值,并记录每个顶点的前相邻节点和后相邻节点;
(4)对内角余弦值从大到小排列,求出最大内角余弦值的顶点,记为A。将该顶点与它的前相邻点(记为B)和后相邻点(记为C)连接成三角形,并检测ABC组成的三角形外接圆是否包含其他顶点,如果包含其他顶点,转到步骤(5),否则转到步骤(6);
(5)取次大内角余弦进行判断,按照步骤(4)重新计算;
(6)从子节点数据结构中去除顶点A,按照步骤(4)重新计算,直到节点数目只有3 个的时候停止,并将这3 个顶点连成三角形,从而结束曲边三角形的三角剖分;
(7)最后将曲边三角形曲边相交的顶点、曲边三角形左曲边1 号节点和曲边三角形的右曲边1 号节点连接成三角形网格。
4 案例说明
为验证算法的正确性与可行性,本文应用有限元分析软件Abaqus 的二次开发语言Python 对算法给予实现,并使用工型长桁三角空隙区域构成的简单多边形对算法进行测试。
同时为了评判网格划分质量,采用节点连元法,将曲边三角形边对应节点相连构成三角形单元。图5是优化前网格剖分结果。
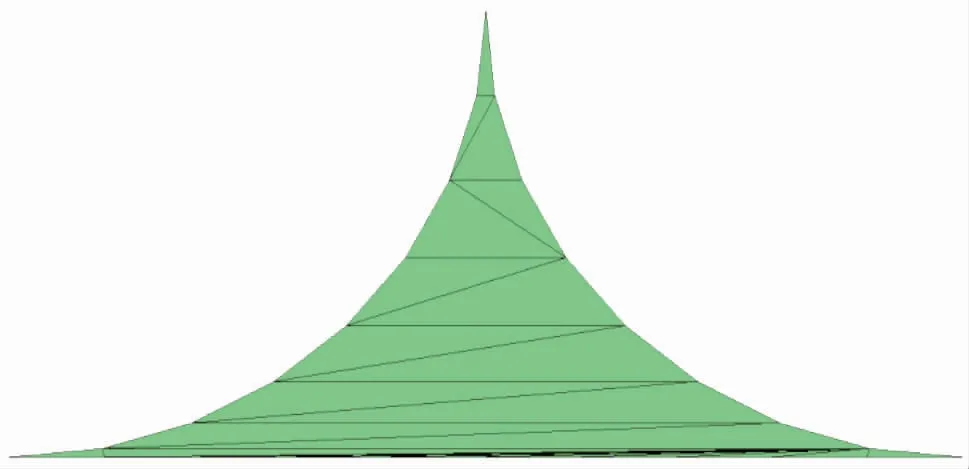
图5 优化前网格剖分结果
优化后网格自动剖分试验结果见图6~8。图6 是捻子条区域初始节点,图7 是自动插入等分节点分布图,图8 是优化后网格剖分结果。表1 是优化前与优化后捻子条区三角形网格质量指标参数对比结果。
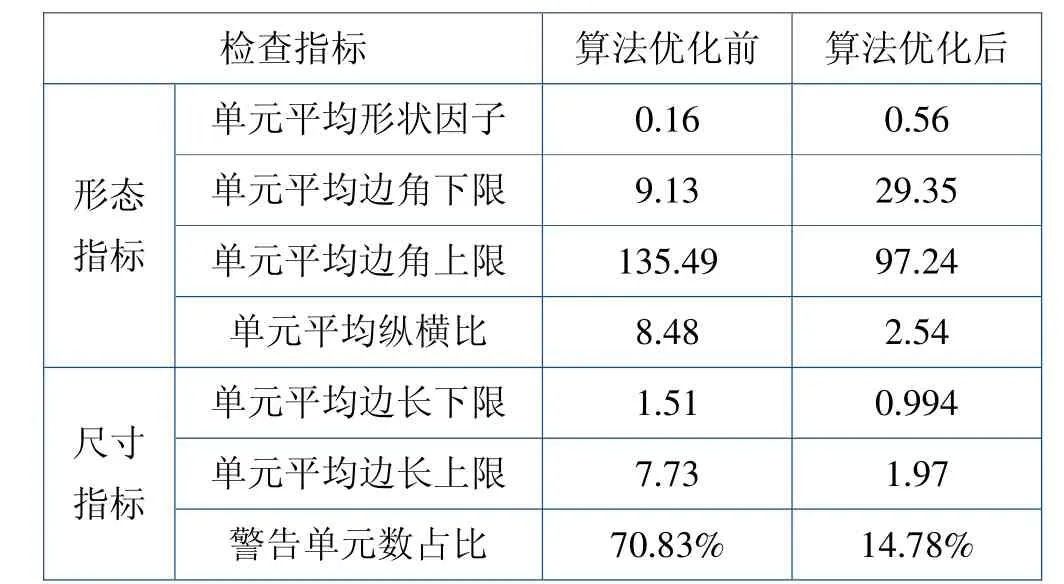
表1 优化前与优化后捻子条区三角形网格质量指标参数对比结果
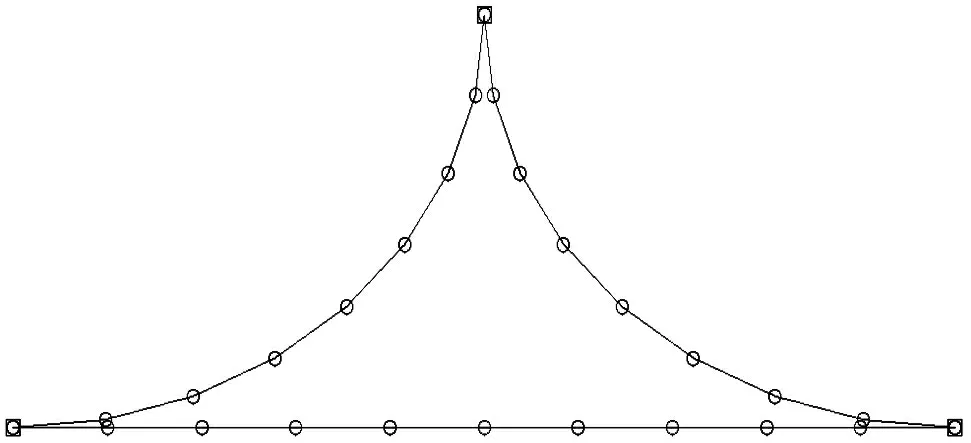
图6 捻子条区域初始节点
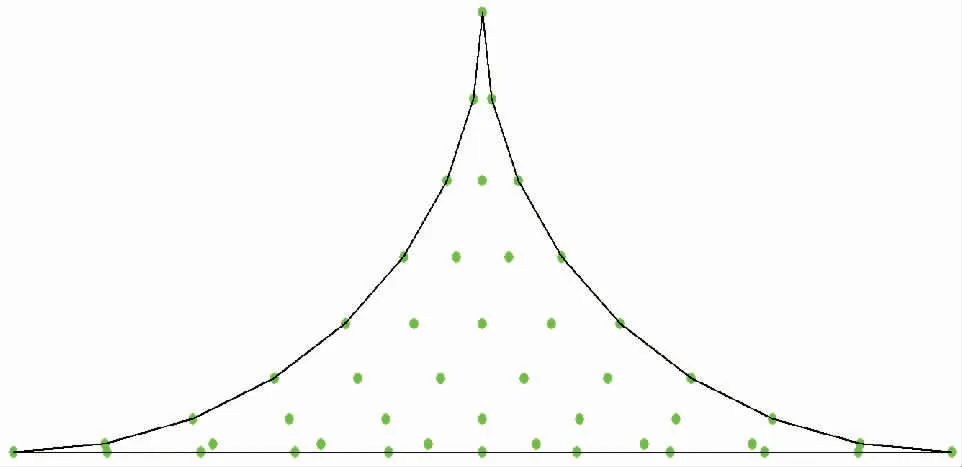
图7 自动插入等分节点
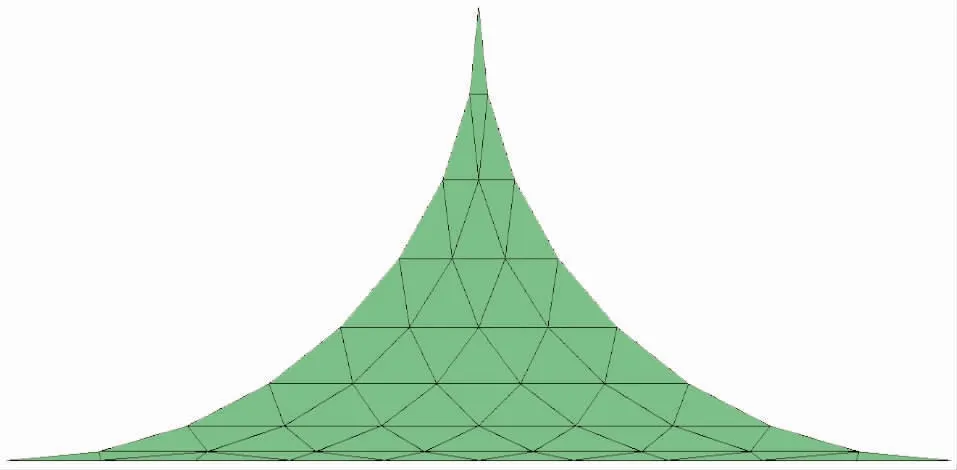
图8 优化后网格剖分结果
5 结语
本文在研究Delaunay 三角网格划分方法基础上,将杨辉三角模型应用到捻子条填充区的网格划分中,从而实现三角形网格的高质量划分,并得出如下结论:
(1)捻子条区域内是否增加节点会显著影响R 区网格划分质量,当将边界上的节点直接相连创建三角形单元时,网格质量差,形状因子只有0.16,单元纵横比超过了可接受值8,发出警告的单元数目占比为70.83%,超过一半以上网格单元质量较差。
(2)通过在捻子条区域内部适当位置自动增加一定数目节点,按照设定的三角形单元网格划分准则,可以剖分出单元质量更好的三角形网格。形状因子提升至0.56,单元纵横比降至2.54,发出警告的单元数目占比也降至14.78%。单元质量得到明显改善。

