基于相互近邻结构体构建的非局部形态学

吕美琪,孙忠贵

(聊城大学 数学科学学院,山东 聊城 252059)

0 引言

数学形态学早在20世纪60年代就被提出,因其严谨的理论基础和丰富的算子实现,至今仍在图像处理的众多领域有着广泛应用,如图像滤波[1],边缘检测[2],特征提取[3],目标识别[4]及图像分割[5]等图像处理的众多领域有着广泛应用。最初的形态学应用主要针对二值图像,随后逐步拓展到灰度图像和彩色图像[6]。其基本思想是结合不同任务采用不同大小与形状的结构体,完成对待处理图像的度量。结构体在本质上是一个与任务先验相关的图像子集,一般分为平坦结构体和非平坦结构体两类。前者的构建仅依赖于空间位置,这意味着其成员具有相同的灰度值;后者,即非平坦结构体,在构建上除依赖空间位置外,其不同成员还往往具有不同的灰度值。在结构体的基础上,一系列的形态学算子被定义出来,其中腐蚀和膨胀是两个最基本算子。其他算子,如开运算和闭运算,一般可通过腐蚀和膨胀算子的组合形式实现。具体到经典形态学(Traditional mathematical morphology,TMM),其算子由平坦结构体定义,通常具备良好的数学性质,其中最具代表性的是保序性和附益性。正是由于这些数学性质使经典形态学具备了坚实的理论基础。然而,由于其结构体的局部性(成员来源于当前像素点附近),经典形态学仍属于局部算法。

非局部算法通过利用图像的自相似性,使得滤波器在处理图像时能够更好的保留边缘及具有周期性的纹理。随着基于片的非局部均值滤波器(Nonlocal means filter,NLM)[7]的提出,许多著名的非局部算法,如K-SVD[8]和BM3D[9]应运而生。非局部算法在近年受到越来越多专家们的关注。许多传统的局部算法也被扩展到非局部或局部非局部结合的形式,并获得了更好的算法性能。事实上,经典形态学的非局部拓展也是近年来一个比较活跃的研究方向。为方便描述,本文将这些拓展算法统称为非局部形态学(Nonlocal mathematical morphologies,NLMMs)。

通过借用图像的非局部相似性权值与像素灰度值直接相加构建结构体,文献[10]最早尝试将经典形态学由局部拓展到非局部,但其算子的许多数学性质无法得到保持。为弥补这一缺陷,文献[11]通过定义结构体系统,提出了一种改进的非局部形态学,使得两个基本算子(腐蚀和膨胀)的附益性得到了保持。遗憾的是,其保序性依然不能成立[12]。并且,上述权值与像素灰度值两个不同量纲因素直接组合相加构建结构体的方式缺乏明确的物理意义,这给实际应用带来困难。针对这一缺陷,近年有相关工作通过将像素灰度值引入非局部权值项增强了其结构体的物理可解释性,同时也保留了相应形态学算子的保序性和附益性[12,13]。需要指出,现有的这些形态学非局部拓展算法,其结构体包括了所有非局部(搜索窗)成员。这种过于宽泛的成员选取,导致结构体的可靠性较差,进而,不可避免会降低算法的有效性[14]。此外,相对于固定结构体的经典形态学,作为一类自适应(结构体可变)算法,NLMMs还具有对噪声较为敏感[15]的缺陷。

基于上述分析,本文提出了一种新的非局部形态学算子(Reciprocal nonlocal mathematical morphology,RNLMM)。首先,我们通过相互近邻(k-reciprocal nearest neighbors,KRNN)[16]策略对文献[12]中的结构体施加对称性约束,有效克服了使用经典K近邻算法可能造成的非对称性,从而使所提形态学算子保持了更多的数学性质。其次,通过形态学算子的串行(局部与非局部相组合)实现,增强对噪声的鲁棒性。理论表明,所提形态学(RNLMM)的数学性质得到较好保持。同时,自然图像与卡通图像的去噪实验均初步验证了RNLMM的有效性。

1 相关工作

为便于算法描述,本节将对相关知识进行简要回顾。首先对经典形态学(TMM)进行介绍,其次描述了非局部均值滤波器(NLM),最后讨论了近年所提出的三种代表性的非局部形态学算法(NLMMs)。

1.1 形态学基本概念及相关性质

数字图像I可以看作是一个从定义域Ω到值域F的数值函数。对于n维图像,Ω是离散空间ℤn的子集,F是图像灰度值的集合。则I可表示为集合Ω到集合F的映射函数x↦I(x),式中x∈Ω且I∈Fun(Ω,F)。

经典形态学(TMM)为图像处理提供了一类广泛的非线性算子。这些算子的本质是待处理图像与结构体之间的相互作用。在形态学算子中,腐蚀和膨胀是两个最基本的算子。其他算子,如开运算和闭运算,都以它们的组合形式来表示。

对于平坦结构体,其对应腐蚀(ε)和膨胀(δ)算子分别定义为

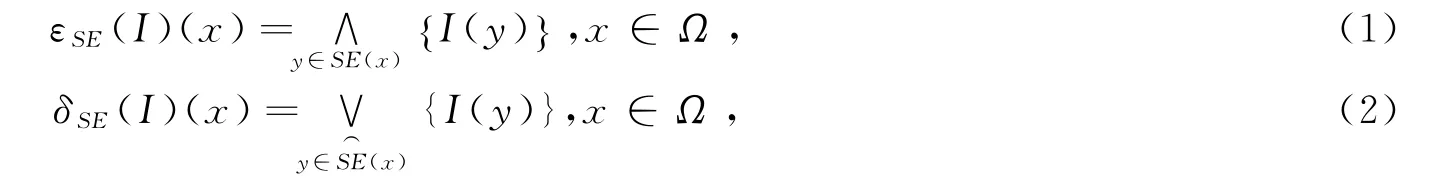
对于非平坦结构体,腐蚀和膨胀算子分别定义为

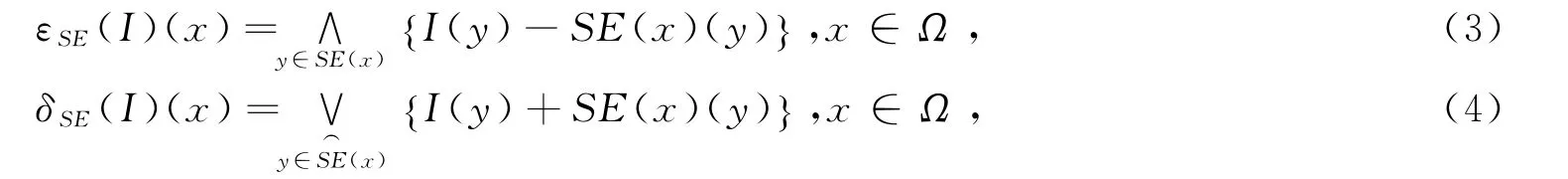
这里SE(x)(y)为像素y处的SE(x)灰度值。

腐蚀和膨胀作为经典形态学的两种基本算子,具有良好的数学性质。其中保序性(定理1)和附益性(定理2)尤为重要。

定理1对图像I∈Fun(Ω,F),

定理2对图像J1,J2∈Fun(Ω,F),

式中保序性是形态梯度定义的理论依据,而形态学梯度在边缘提取中有着重要应用[6]。另一方面,附益性刻画了腐蚀与膨胀算子之间的密切关系,从而保证了闭运算和开运算的数学合理性。

开运算和闭运算定义如

需要注意,尽管经典形态学的算子具有上述良好的数学性质,受结构体局部性的影响,其仍属于局部方法。

1.2 非局部均值滤波器

与局部滤波器相比,NLM有两个明显的优点。一方面,它利用非局部邻域的加权平均估计像素值,可以很好地利用图像的自相似性;另一方面,通过图像块间的块匹配来计算权重,对噪声具有鲁棒性。

给定待处理图像I,用非局部均值算法计算像素的估计值,如

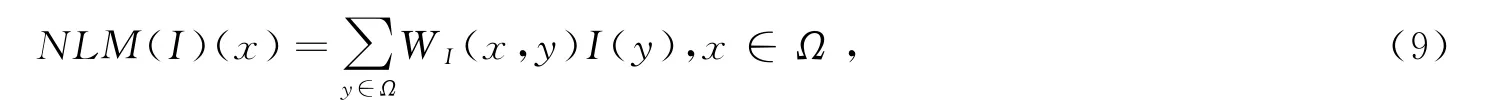
式中权值W I(x,y)为以像素x为中心的片P I(x)和以y为中心的片P I(y)之间的相似性,下标表示所有的计算依赖于图像I。具体来说,相似性权值定义为

式中

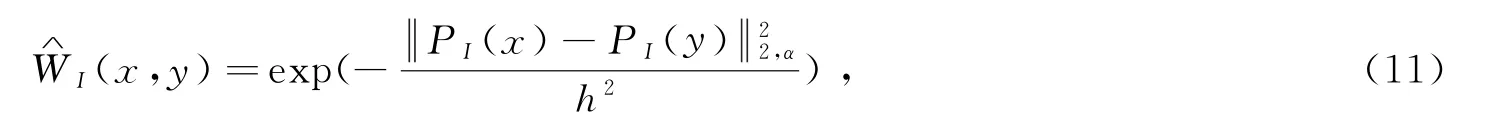
这里h为平滑参数,为具有标准差α的高斯加权L2范数。此外,0≤W I(x,y)≤1且y)＝1。

尽管非局部均值滤波器的实施非常复杂,但它提供了良好的滤波结果。因此,非局部方法已成为设计滤波器的主流。

1.3 现有的非局部形态学改进

Philippe Salembier最早尝试借用NLM的非局部权值,对经典形态学进行非局部拓展[10]。与传统的结构体被限制在局部区域的方法不同,此算法在非局部搜索窗(甚至整个图像)上定义结构体。其中,结构体是非平坦的,其成员灰度值直接借用NLM中的片相似性。与经典形态学(公式(3)和公式(4))定义的形式一样,在文献[10]中非局部形态学,即NLMM的两个基本算子(腐蚀和膨胀)分别定义为

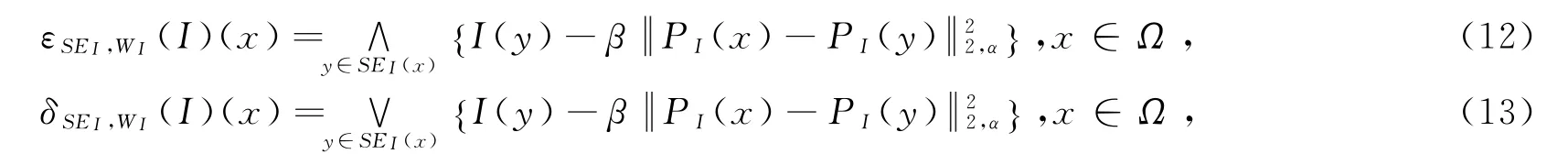
式中I仍为待处理图像,SE I为定义的结构体,β是控制非平坦程度的参数。

在4类产品中，2007年，约旦的RCA为1，说明该产品出口具有中度的国际竞争力；在2008年、2009年中，约旦的RCA介于1.25-2.5之间，说明该产品出口具有较强的国际竞争力；2010年-2016年，约旦的RCA均小于0.8，说明约旦在该类产品出口中，国际竞争力较弱；在中国的RCA小于0.1，该类产品出口国际竞争力较弱。

不幸的是,在上述的非局部拓展过程中,腐蚀和膨胀算子的保序性和附益性都丢失了。文献[11]定义了一个结构体系统,即对任意x,y∈Ω,相应的结构体应满足如下自反性与对称性

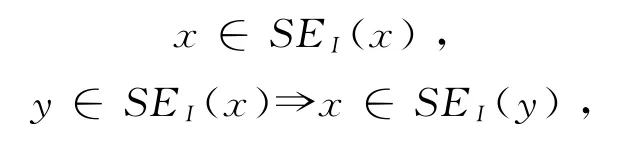
此外,文献[17]指出为了使算子保持好的数学性质,其结构体应当是固定的,即“一旦自适应邻域从初始输入图像导出,就必须对其进行固定”。

基于此结构体系统,文献[11]的NLMM所相应的腐蚀和膨胀算子被重新定义为

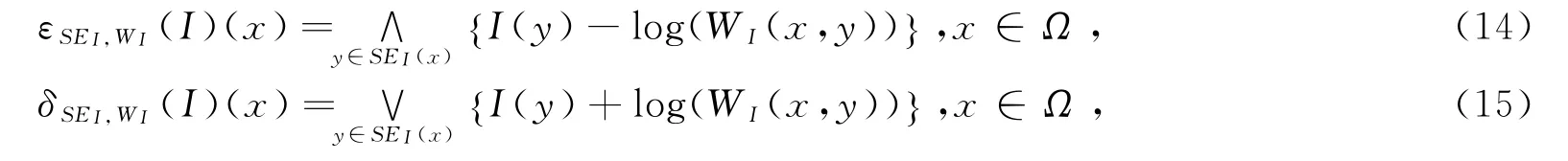
式中SE I(x)来自结构体系统,W I(x,y)为公式(10)中所定义的非局部权值。

我们在文献[12]指出,尽管上述两个算子的附益性得到了保持,其保序性依然不能满足。且相应的非平坦结构体是通过两个不同量纲的因素(即灰度值和权重)直接相加得到,丢失了物理上的可解释性。如文献[18]所述,“当使用非平坦结构体时,它们的灰度值应该与输入图像的灰度值具有相同的量纲”。为弥补这一缺陷,文[12]通过将灰度值引入结构体的定义,相应NLMM的腐蚀和膨胀算子分别为

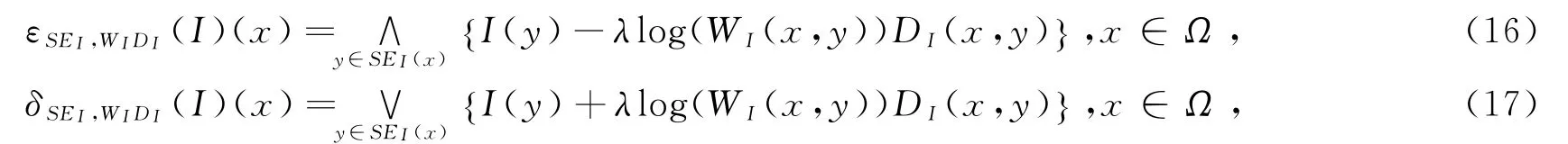
这里λ是一个控制结构体的非平坦范围的参数。作为一个通用模型,其中W I(x,y)是一个一般的非局部相似性度量,不再局限于NLM中的权值,D I(x,y)表示像素x与y的灰度值之间的差值。在减小量纲差异的同时,文献[12]还从理论上保证了上述两个算子的附益性和保序性。

然而,正如文献[14]所指出,在非局部滤波算法中,将整个搜索窗中的所有像素点全部用于当前像素点的估计,会导致过多不可靠像素点的参与,致使估计精度下降。上述所介绍的三个非局部形态学(即NLMMs)[10-12],结构体成员均包括了整个搜索窗,这显然会削弱其相应算子的性能。此外,作为一类自适应算法,这些算子也极易受到噪声的影响[15]。针对这些现有非局部拓展算法存在的缺陷,本文提出了一个基于相互近邻结构体的非局部形态学。

2 基于相互近邻结构体的非局部形态学

本文工作,即RNLMM,是在文作[12]的基础上展开的,其改进主要体现在两个方面。首先,利用相互近邻策略对结构体的构建施加约束,提高其成员的可靠性;然后,将经典形态学(局部)与非局部形态学相结合,设计出一个算子的串行实现方式,有效提高了其对噪声的鲁棒性,并且理论证明了相应算子的保序性与附益性能够同时得到保持。下面分别围绕这两部分内容展开论述。

2.1 基于相互近邻的非局部结构体构建

如公式(16)与公式(17)所示,文[12]采用将非局部权值与像素灰度值相乘的方式构建结构体。正如上述分析,这种结构体的构建方式会导致成员的不可靠性。针对这一缺陷,我们采用相互近邻策略[16]进行结构体构建。这样的构建方式不单能够筛选出可靠的结构体成员,还能使相应结构体具有对称性。后者对算子数学性质的保持尤为重要[11]。

首先以非局部权值作为度量函数,利用K近邻的方法选取权值较大的像素点作为当前像素x的候选结构体成员,即

式中y k为像素x的第k个近邻,成员的置信度由参数k决定。

进一步,通过施加对称性约束,便可得到如下基于相互近邻的结构体

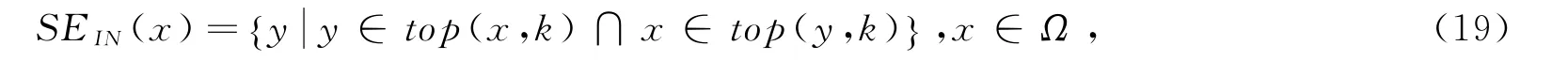
由于每个像素点与它自身的相似性最大,显然结构体SE IN(x)在满足对称性的同时也满足了自反性。

相应地,基于上述结构体,我们得到非局部形态学腐蚀和膨胀两个基本算子的初步形式

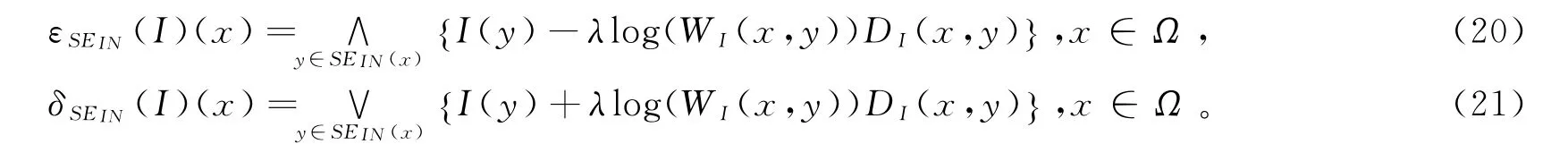
下面将其与经典形态学的相应算子进行串行组合得到非局部形态学(RNLMM)算子的最终形式。

2.2 串行形态学算子及其性质证明

尽管非局部形态学能够较好保持图像边缘、纹理等周期性信息,但其本质上的自适应性会使相应算子容易受到噪声的影响,即对噪声不够鲁棒。相比之下,经典形态学采用固定结构体,其对应算子具有平移不变性,从而对噪声展现出了更好的鲁棒性。这一事实启发我们将具有固定结构体的经典形态学算子与上述非局部形态学算子(式(20)和式(21))进行串行组合,以期在更好地保持边缘及周期性纹理的同时也能对噪声较为鲁棒。本文非局部形态学,即RNLMM,所最终采用的两个基本算子定义如

定理3和定理4表明,上述腐蚀和膨胀算子的保序性和附益性均得到保持。

定理3(保序性)对任意图像I∈Fun(Ω,F),有ε(I)≤I≤δ(I)。

证明由结构体的自反性,即x∈SE IN(x)与x∈SE(x)对∀x∈Ω成立,有,即,则有。根据公式(5)中,有J≤。类似可证。

定理4 (附益性) 对任意图像。

证明 由相互近邻结构体的构建过程可知本文RNLMM的结构体具有对称性。同时,为了简化证明过程,分别用符号T1和T2表示膨胀与腐蚀操作,即。

在上述准备基础上,开展证明

即

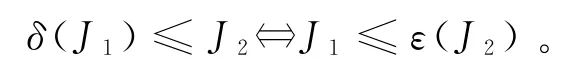
定理得证。

3 分析

通过图像去噪初步验证所提RNLMM的有效性。考虑到经典形态学中结构体越大,对图像的细节信息破坏越严重,我们在RNLMM的串行算子中,经典形态学部分的结构体半径设置为1。故试验所涉及的比较算法除了前面所介绍的三个代表性的非局部形态学(NLMMs)[10-12],还有结构体半径为1的经典形态学。需指出,由于经典形态学的高效性,本文将其与非局部形态学相结合的串行算子实现在时间复杂度上较其他非局部形态学并未有明显增加。同时,尽管结构体构建时KRNN的引进引起复杂度的增加,幸运的是,形态学的所有操作算子共享同一个结构体,也就是说KRNN的运算在本文RNLMM中只需进行一次,且其复杂度也明显小于非局部运算本身。故本算法在复杂度上较其他非局部算法没有明显增加。

所具体采用的形态学滤波为OCCO滤波器[19](取开运算-闭运算和闭运算-开运算的平均值)。由于其输出具有自对偶优势,OCCO已成为形态学去噪的一种典型方法。我们分别在一幅自然图像和一幅卡通图像上进行不同噪声程度的去噪实验,并采用客观的峰值信噪比(Peak Signal to Noise Ration,PSNR)和主观视觉效果作为评价指标。根据经验,我们令所提算法中的结构体构建的近邻数k＝50。为了公平起见,其他实验比较的非局部算法中所涉及参数,如结构体大小、图像块大小、高斯平滑参数等均被设为其原始文献的推荐值。

图1和图2是低噪声场景(σ＝20)下的去噪实验。由结果可以看出,经典形态学在去除噪声方面表现良好。尽管NLMMs[10-12]获得了较为平滑的视觉效果,由于其对噪声的鲁棒性较差,图像的细节信息并未得到较好保持。本文所提RNLMM的结构体的串行实现策略,实现了经典形态学与非局部形态学的较好折中。相应输出结果在结构保持和去噪之间取得了较好的平衡,其无论在视觉效果还是PSNR指标均优于其他方法。

图1 比较了不同形态学算法在噪声水平σ＝20下对House图像的PSNR值及视觉效果

图2 比较了不同形态学算法在噪声水平σ＝20下对Chessboard图像的PSNR值及视觉效果

图3和图4展示了高噪声场景(σ＝40)下的实验结果。此种情况下,经典形态学已不能很好地去除噪声,且产生了棋盘效应[20]的视觉缺陷。尽管NLMMs[10-12]通过非局部策略能够有效去除噪声且避免了棋盘效应,但过光滑现象依然没有解决。在此条件下,RNLMM在所有算法中仍然保持着最好的实验结果。

图4 比较了不同形态学算法在噪声水平σ＝40下对Chessboard图像的PSNR值及视觉效果

图3比较了不同形态学算法在噪声水平σ＝40下对House图像的PSNR值及视觉效果

4 结论

本文提出了一种新的非局部形态学算子,即RNLMM。一方面,与其他非局部形态学算法不同,本文通过相互近邻策略有效提高了结构体成员的可靠性。另一方面,为提高算法对噪声的鲁棒性,RNLMM采用串行方式构造算子,实现了经典形态学与非局部形态学的很好折中。且理论上保证了其相应算子依然具备良好的数学性质。初步的去噪实验也验证了RNLMM的优良性能。需要注意的是,非局部运算本身是造成非局部形态学算法复杂度高的主要原因,近年已有一些相应加速算法[21,22]被提出,如何将其用于非局部形态学改进,值得尝试。此外,如何将这些非局部形态学的场景由单模态推广至多模态也值得尝试。最后需要指出,近年,图形态学已成为一个经典形态学的非局部拓展的重要研究方向[23]。故将本文RNLMM的相关策略扩展到图上也极具研究价值。