考虑能耗分段的物流无人机调度模型

任新惠，武 彤

1.中国民航大学 经济与管理学院，天津 300300

2.中国民航大学 交通科学与工程学院，天津 300300

随着科技的进步，电子商务快递业的发展，物流配送量与日俱增，从2010 年的23.4 亿件增长至2020 年的821亿件，10年增长3 408.5%。传统的地面车辆也很难在短时间内配送如此多的订单，且车辆容易受到地面复杂交通、山川、河流和障碍物的影响，因而延长派送时间与成本。基于此物流无人机（unmanned aerial vehicle，UAV）逐渐兴起。无人机飞行速度快，成本低，不受地面复杂交通与一般基础建筑物影响，配送效率高[1]。2013年亚马逊推出Prime Air 项目，德国邮政推出Parcelcopter 项目[2]，使用无人机直接将包裹交付于需求点。2016年起京东、百度、阿里巴巴等也逐渐开始使用无人机交付包裹。但UAV大多使用电池供电，续航时间短，运载能力有限[3-7]。考虑无人机能耗的交付路线规划成为研究重点。

目前在进行无人机路径规划中，大多单纯对无人机飞行范围、飞行时间等进行简单约束，构建的模型不能满足实际运行约束，导致部分配送路线不可行。因此精准估计有效载荷、速度[8-11]等因素对电池能耗的影响变得至关重要。为计算UAV 在配送中的能耗，Dorling 等人[2]提出有效载荷与无人机能耗的线性模型，根据有效载荷优化电池重量，可将能量转换效率提高10%左右，同时可以根据电池能量、功率等推出最大飞行时间，从而对无人机进行约束。Maryam[12]提出电池消耗率的概念（battery consumption rate，BCR），有效载荷与BCR存在正相关线性关系，影响电池续航时间。在不考虑BCR的情况下，有近60%的配送方案因电池电量不足而不可行。Cheng[13]与Muarry[14]认为与线性能耗模型相比非线性能耗模型可以更加准确地描述无人机飞行过程的能耗。使用线性模型求解部分路线在非线性模型下是不可行的，且线性模型与非线性模型求解的能耗相差近9%。为更加全面描述能耗变化，Muarry[14]将无人机飞行分为起飞、巡航、降落与悬停4种状态，各个状态的速度与功率是各不相同常值，因而4 种状态能耗不同，通过优化不同飞行阶段的飞行速度减少飞行总能耗。

Troudi[15]则提出当一架无人机为多个需求点提供服务时，总能耗与各个服务阶段的包裹数量和距离有关。实际运行中，无人机需要交付多个包裹，能耗不仅仅依赖包裹数量同时与包裹重量、投递顺序和每段飞行距离有关，能耗可能也存在较大差异。能耗计算的准确与否，直接影响到无人机的配送任务，甚至是能否安全返回仓库。考虑到有效载荷与配送路径的方向性，本文提出考虑能耗分段的物流无人机调度模型，设计改进差分进化算法求解，结果表明能耗分段模型准确计算各个飞行阶段能耗产生可行解的同时减少飞行路长。

1 问题描述

与使用卡车进行配送不同，城市配送的小型无人机不仅配送速度快、成本低而且不会存在交通拥堵问题，但其在执行配送任务时，存在能量与有效载荷限制问题，只能携带少量包裹飞行较短的距离，因此为了安全高效完成配送任务，同时提高无人机电池利用率，需要结合无人机特性考虑其能量消耗过程。无人机飞行过程中，无人机本身的重量与包裹重量同样对飞行能耗有较大的影响。当一架无人机按序同时为多个需求点提供服务时，需要逐个卸载携带包裹，那么其有效载荷随着包裹的逐件卸载而减小[16]（见图1），因此无人机配送能量消耗速度也随着有效载荷的减小而分阶段减小，其飞行能耗如图2所示。

在整个配送中，每架无人机的能量消耗速度是随有效载荷减小而逐渐减小的，无人机需在电池能量限制下安全返回配送中心，待完成装载包裹与新电池后，按调度方案开始下一次配送任务。如单纯限制无人机飞行时间或飞行距离无人机可能因电池电量不足，而无法完成所有的配送任务，同时也无法安全返回仓库，反之电池得不到充分利用，需要派遣更多的无人机或更换更多的电池为需求点提供服务，从而使得配送成本增加。因此首先提出能耗分段模型，精确计算物流无人机在配送过程的能耗，保障实际配送方案的实施。基于此构建无人机调度模型，达到无人机配送多个用户且距离最短。

本文假设无人机配送中心有多架最大有效载荷为5 kg 的无人机可为n个需求点提供服务。配送中心编号为0，集合Ca={1,2,…,n}表示n位顾客。根据调度方案，在每架无人机有效载荷的限制下，多架无人机携带多个需求点的包裹从配送中心出发，逐个按序为需求点提供配送服务，待所有包裹配送完毕后返回仓库，更换电池装载下一批需要配送的包裹。

考虑能耗分段的物流无人机调度模型中，使用标准算例库中的问题数据，所有需求点位置坐标、需求量、仓库位置坐标已知。

本文问题假设如下：

（1）无人机类型相同使用电池相同。

（2）忽略天气对对无人机电池续航能力影响（风、温度等）。

（3）不考虑需求点时间窗。

（4）无人机不需要充电，更换电池，且不考虑换电池时间。

（5）所有需求点位置与需求已知，所有需求点都需得到服务。

（6）每个需求点的配送需求由一架无人机满足。

（7）每架无人机可为多个需求点提供服务。

（8）无人机开始配送任务时使用满电量电池。

（9）只设立一个仓库（配送中心）。

2 基于能耗分段的物流无人机调度模型

2.1 模型符号

根据问题描述模型符号定义及解释如表1。

表1 模型符号定义及解释Table 1 Model symbol definition and interpretation

2.2 物流无人机配送能量消耗过程建模

根据无人机配送能量消耗过程建立模型[13，17]，电池功率Pij可以表示如下：

式（1）为无人机从需求点i飞至需求点j时的飞行功率，其中W为无人机自重，m为无人机携带货物重量，Vij为无人机从i需求点飞至j需求点的速度，η为螺旋桨动力传递效率，γ为无人机飞行升阻比，e为无人机电子元器件能耗。无人机从需求点i飞至需求点j所需时间以及能量如公式（2）、（3）：

2.3 无人机调度模型构建

根据问题描述和问题假设，考虑无人机能耗分段消耗的特点，无人机调度模型建立如下：

等式（11）为目标函数，求解最小化无人机飞行距离。式（12）、（13）消除子回路。式（12）保证从仓库出发执行任务的无人机完成所有任务后返回仓库。式（13）表示每个需求点都有一个入口和一个出口。式（14）确保一个包裹仅由一个执行任务m的无人机k提供。式（15）保证执行任务m的无人机所需能量小于其电池能量。式（16）表示执行任务m的无人机k从需求点i飞至j需求点所需时间。式（17）表示每位顾客都被服务。式（18）表示如无人机k执行任务m，其至少交付一个包裹。式（19）表示无人机携带货物重量小于其最大有效载荷。式（20）保证决策变量xijkm、zikm为0，1变量。

3 算法设计

为解决考虑能耗分段的物流无人机配送问题，提出改进差分进化算法，该算法是在遗传算法的基础上提出，通过生成随机的初始种群，计算种群个体适应度后判断是否达到终止条件，若达到则输出最优解，反之则需要进行变异、交叉与选择等步骤产生下一代种群，继续迭代至满足终止条件。基本差分进化算法具有较好的鲁棒性与可靠性，但其一般随机生成初始种群，且规定种群中的个体交叉概率为常数，前期算法的搜索效率较高，但中后期得到结果多数不满足局部搜索约束导致算法效率降低[1，18]。为解决此类问题，本文引入了贪婪初始化种群与自适应贪婪交叉，克服基本差分进化算法计算效率低问题。

3.1 算法流程

改进的差分进化算法使用贪婪初始化生成初始种群，首先从需求点集合Ca中随机选取一需求点作为初始服务需求点，按照距离最近原则选择下一服务需求点，直至所有需求点服务完毕，生成初始种群，提高初始种群质量。自适应贪婪交叉算子则是将种群中交叉概率改为与最大迭代数和当前迭代数相关的数值，如式（21）：

其中，gen为当前迭代次数，MAXGEN为最大迭代次数。种群交叉概率随着迭代次数增加逐渐增加，同时满足了全局搜索与局部搜索的性能要求，提高收敛精度，加快寻优速度。为了保持较好的前后关系，采用贪婪顺序交叉，随机选取两个体基因片段交换，将第二个切点后，第一个基因起列出原基因顺序，删除已有基因后依然从第二个切点后，第一个位置起顺序排列，得到两个无重复基因新子代，丰富了种群的多样性，具体操作如图3所示。

改进的差分进化算法具体步骤如下：

步骤1 参数初始化，包含种群最大迭代次数MAXGEN，种群规模NP，令当前迭代次数gen=0。

步骤2 贪婪初始化生成初始种群。

步骤3gen=gen+1。

步骤4 随机选取当前目标个体Ni之外另外3个互不相同的个体。

步骤5 执行变异操作，产生变异个体Xi。

步骤6 生成自适应种群交叉率。

步骤7 计算变异个体Xi适应度，执行选择操作。

步骤8 变异个体Xi与当前目标个体Ni执行交叉操作，生成新个体Yi。

步骤9 计算新个体Yi适应度，再次执行选择操作。

步骤10 当前目标个体下标i=i+1，返回步骤4，直至i=NP，执行步骤11。

步骤11 判断当前迭代次数gen是否达到最大迭代次数，若到达则跳转步骤12，若未达到返回步骤3。

步骤12 输出最优结果。

改进差分进化算法流程图如图4所示。

3.2 算法性能测试

为了验证改进差分进化算法的稳定性、收敛性与稳定性，使用网站http：//www.bernabe.dorronsoro.es/v-rp/中CVRP 标准算例库中的问题A-n32-k5 数据，采用MATLAB R2016b 编程；运行环境为64 位Windows 10操作系统，处理器为AMD锐龙5 3500U四核八线程，主频2.10 GHz，运行内存12 GB。分别设定迭代次数为300、200 与100，种群规模设置为50、100、150 和200，分别组合测试，计算结果如表2。同时测试将最大迭代次数设置为100，种群规模设置为100时，改进差分进化算法的收敛性如图5。

表2 A-n32-k5数据测试结果Table 2 A-n32-k5 data test results

由表2结果可知，改进差分进化算法在求解VRP问题的稳定性明显优于基本差分进化算法，测试结果全部为最优值，而基本差分进化算法随着种群规模与迭代次数的增加，其求解结果才逐渐变优。图5则显示改进差分进化算法初始种群质量明显优于基本差分进化算法，且收敛速度较快。

4 算例分析

为验证模型有效性，本文使用CVRP标准算例库中的问题A-n32-k5、A-n37-k5、A-n48-k7，以及A-n53-k7为基础数据，根据本文建立的考虑无人机能耗分段模型修改部分数据生成算例C-n32-k5、C-n37-k5、C-n48-k7 和C-n53-k7，每个算例都含有一个仓库，分别包含31、36、47、52个需求点，其中算例C-n32-k5、C-n48-k7中需求点于仓库位置处呈发散式分布，C-n37-k5、C-n53-k7 中需求点分布于仓库周围，两种分布方式见图6。

假设无人机最大有效载荷为5 kg，为确保每个包裹都可由无人机配送测试算例中的每个需求点的需求量为标准算例中的0.05倍。无人机自重为9 kg，携带电池重量为1 kg，电池电量约为0.25（kW·h）/kg。根据无人机尺寸可知其最大飞行功率为1 781 W，整个飞行过程中无人机电子元器件能耗e为100 W，升阻比γ为3，能量转换效率η为0.5，根据式（8）可得系数k为933。

4.1 考虑能耗分段无人机调度模型优化求解

（1）计算不考虑能耗及考虑能耗下最短配送路径方案的能耗情况

根据无人机能耗公式（5）与（10），计算算例的最优最短配送路径方案能耗情况。再加入电池能量限制但不考虑能耗分段情况下求得最短配送路径的能耗。使用改进差分进化算法设置种群数100，迭代数300，以C-n32-k5为例，计算结果如表3所示。

从表3结果可以看出，C-n32-k5算例中共需5架无人机，在不考虑能耗的情况下，求得配送方案路径最短，但其中两架无人机所需能量分别为0.38 kW·h与0.33 kW·h，在实际运行中均超出电池实际电量0.25 kW·h。加入电池能量限制后，所有调度方案变为所需能量均小于电池最大能量0.25 kW·h，但因能耗限制导致提供服务无人机数量增加至6架。同时单架无人机服务需求点数减少，服务顺序发生改变。由于增加无人机提供服务，因此总飞行距离增加。算例C-n32-k5、C-n37-k5、C-n48-k7与C-n53-k7加入能量限制后配送方案路长增量百分比见表4所示。

表3 C-n32-k5数据测试结果Table 3 C-n32-k5 data test results

表4 考虑能耗前后配送方案路长及增量百分比Table 4 Incremental percentage of route length of distribution scheme before and after energy consumption

表4 结果显示C-n32-k5 与C-n48-k7 路长增幅达到了30%以上，C-n37-k5 与C-n53-k7 路长增幅在20%以下。出现此类情况与需求点分布有关，当增加能耗限制后，单架无人机服务次数减少，需要更多的无人机提供服务。由于C-n32-k5与C-n48-k7中的需求点于仓库位置发散式分布，仓库距各个需求点距离比需求点分布于仓库周围的C-n37-k5 与C-n53-k7 更长，因此路长增幅较大。加入能量限制后配送方案存在一定路长增幅但求得所有配送方案均为可行方案，能耗都在电池电量范围内，符合实际运行情况。考虑到无人机携带包裹逐渐减少，有效载荷逐渐减小，因此还需进一步根据能耗分段模型求解，使结果更加准确。

（2）计算考虑能耗分段下配送路长

为进行对比分析，使用能耗分段模型求解考虑能耗后生成路径能耗情况列于表5。

表5 考虑能耗与考虑能耗分段下配送路径能耗Table 5 Considering energy consumption and energy consumption of distribution path under energy consumption segmentation

利用能耗分段模型考虑无人机电量消耗速度随有效载荷逐渐减小而减小后，求解配送路径所需能量均减少，所有算例配送方案所需能量平均减少了14%～18%。造成差异的主要原因有以下：不同的调度方案中无人机总有效载荷不同；每架无人机服务次数不同；不同需求点距仓库距离以及各个需求点之间的距离不同；每个包裹的重量不同；包裹卸载顺序不同，电池能耗减小速度不同，能耗不同。

（3）计算关于能耗不同约束下的配送路长

为探究不同约束条件对配送方案路长分影响，分别计算不考虑能耗的配送方案路长、只加入电池能量约束的配送方案路长、既加入电池能量约束又考虑电池能耗分段情况下的配送方案路长，如表6所示。

表6 3类不同约束下配送路长Table 6 Distribution road length under three different constraints

由表6 可见，不考虑能量限制的配送方案路长最短，但部分解为不可行解，因为实际所需电量超出电池最大电量；只考虑能量约束不考虑能耗分段的配送调度方案路长增加7%～39%，但所有方案实际所需电量均小于电池最大电量；考虑能耗分段后，单架无人机有效载荷增加或可以为更多需求点提供服务，使用更少的无人机满足所有需求点，调度方案的总路长减小，尤其是运用改进差分进化算法后路径减少程度（优化）最大。

未考虑能耗、考虑能耗、考虑能耗分段（基本差分进化算法求解）与考虑能耗分段（改进差分进化算法求解）路长增幅百分比的比较见图7。

如图7所示，使用改进差分进化算法求解能耗分段的配送方案路长相比于最优配送方案路长增加1%～24%，平均增加9%，相较于不考虑能耗分段模型只加入电池能量约束调度方案能耗减小7%～23%，路长平均缩短11.9%。使用基本差分进化算法求解配送方案路长增加4%～26%，平均增加14%，从结果可看出改进差分进化算法性能优于基本差分进化算法。改进差分进化算法可以稳定求解小规模与中规模无人机路径问题，且求解质量较高。

无人机调度模型增加了无人机自身电量消耗分段特点的考虑，使得研究更贴合实际。因此求解配送方案不仅满足了无人机电池电量约束，同时考虑最小化无人机派遣数量，总路长更短，提高了无人机的利用效率。

4.2 敏感性分析

为探究能耗分段情况下电池数量对配送方案的影响，使用改进差分进化算法分别测试当无人机携带1～3组电池时配送路长以及无人机数量，设置种群数目100，迭代次数为300。假设一组电池重量为1 kg，电量为0.25 kW·h。当装载1 组电池时，无人机最大有效载荷为5 kg，装载2组、3组电池时，最大有效载荷分别为4 kg与3 kg。测试结果如表7，其中b为电池使用组数，L为所有UAV配送总路长，N为UAV使用数量。

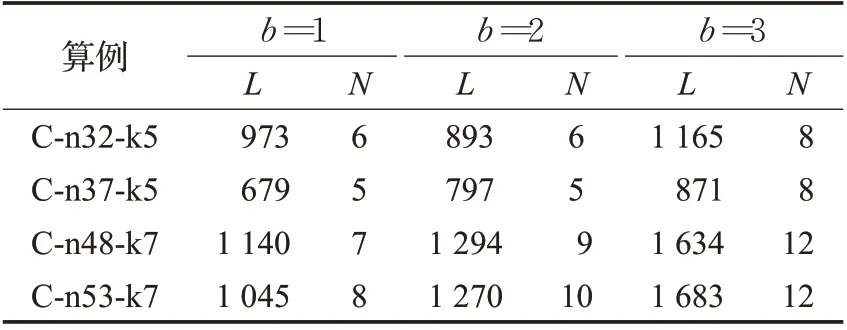
表7 电池使用组数对配送路长及无人机数量影响Table 7 Influence of number of battery groups on length of distribution and number of UAVs

由表7 可知，在算例C-n32-k5 中，路长随着电池组数的增加先减小后增大，电池数量为2 时，无人机最大有效载荷为4 kg，UAV使用数量为6，与电池数量为1时使用UAV 数量相同，说明增加的电池在满足其配送所需能量扩大其飞行范围的同时，不影响无人机携带包裹分配，6架UAV可以携带算例C-n32-k5中所有需求点包裹与增加的电池。但当电池组数为3时，无人机最大有效载荷为3 kg，单架无人机最大有效载荷减小，可携带包裹数量减少。C-n32-k5 算例中需求点数与其需要包裹重量一定，因此需要更多的无人机满足所有需求点的需求，路长增加。在算例C-n37-k5、C-n48-k7 与C-n53-k7 中，配送路长与UAV 使用数量随着电池组数的增加而增加。在中规模算例中，一架无人机给多个需求点提供服务，有效载荷利用率高，电池组数增加能量增加，但最大有效载荷减小，在包裹数一定的情况下需要更多的无人机为需求点提供服务，路长增加。由此可见，电池组数影响有效载荷进而影响UAV使用数量及可飞行最大路长，其取值在制定配送方案时要进行权衡，应根据需求点数、包裹数、包裹重量与最大有效载荷确定，从而充分利用无人机有效载荷减少配送路长。

5 结论与展望

针对物流无人机配送过程不考虑能耗而导致部分求解方案不可行，将总有效载荷纳入能耗计算导致配送方案效率低等问题，本文基于车辆路径问题模型VRP，提出能耗分段无人机调度模型。根据配送阶段与实时有效载荷量精确计算无人机每段飞行能耗，以最小化总飞行路长为目标，调度无人机为多个需求点提供服务。结果表明：

（1）构建无人机调度模型中考虑无人机能耗分段约束，结果更加符合无人机实际运行。

（2）改进差分进化算法通过测试，优于基本差分进化算法，且收敛速度较快。

（3）考虑能耗分段的无人机调度模型求解的配送路径所需能量较不考虑能耗分段减少7%～23%，而路长增幅较不加入能耗限制模型平均增加9%，无人机交付完所有包裹后可以安全返回仓库。

本文提出的考虑能耗分段的无人机调度模型可以在保证满足所有需求点的情况下，最小化无人机使用数量与所有执飞无人机飞行总距离，精确每架执飞无人机执行一次任务为多个需求点提供服务时所需能量，提高每架无人机与电池利用率，减小配送成本。本文假设所有阶段无人机飞行功率一致，未来可进一步考虑无人机在起飞、巡航、降落与悬停过程中的飞行功率，更精确能耗模型，进一步优化配送方案。