n元二次函数的极值公式
管山林, 马江涛, 郭 震
(云南师范大学数学学院,昆明650500)
1 引 言
n元二次函数求极值的问题在线性规划、最优化理论等理论中是非常重要的一类问题.因此很多学者都对这类问题进行了研究.参考文献[1]讨论了极值点的公式,参考文献[2]讨论了齐次情形极值存在的条件,参考文献[3]给出了一些极值存在的条件和极值公式的讨论,参考文献[4]讨论了极值存在的条件,参考文献[5]进行了极值存在条件的讨论和一次项消去的充要条件,参考文献[6]给出了正定和负定情况的极值公式的行列式表达,参考文献[7]讨论了n元二次函数正定的充要条件,参考文献[8]给出了二元二次函数的极值公式, 并进行了n元二次函数极值存在必要条件的讨论,参考文献[9]给出了正定和负定情况相对完善的极值存在条件和极值公式的总结归纳,参考文献[10]从最优化的角度讨论了齐次情形的公式.
针对该问题的研究现状, 待解决的问题是给出完整的极值存在的充要条件, 非满秩(半正定或者半负定)情形极值公式如何表达, 以及如何统一非满秩(半正定或者半负定)和满秩(半定或者负定)的极值公式. 本文完整的讨论了极值存在的充要条件和极值的一般公式,得出了统一而简洁的结果. 这对于教师教学和学生学习、理解、记忆都是有非常帮助的.
设f(x)=f(x1,…,xn)为n元二次函数, 其表达式为
其中apq关于指标p,q是对称的, 其中1≤p≤n+1, 1≤q≤n+1(总可以选到系数使得apq是对称的).记矩阵A=(apq), det(A)为A的行列式,Apq为矩阵A中元素apq的代数余子式.类似的, 记矩阵A0=(aij), 其中1≤i≤n, 1≤j≤n, det(A0)为A0的行列式, (A0)i为A0的第i个顺序主子式.O为n阶零矩阵.
2 主要结果
定理1设f(x)是上述形式的n元二次函数(A0≠O), 则
(i)f(x)极值存在(且唯一)当且仅当下列情况之一成立:
① (A0)i>0,∀1≤i≤n或者(-1)i(A0)i>0,∀1≤i≤n.此时其极值点和极值分别为
若(A0)i>0,∀1≤i≤n, 则f(x0)是极小值; 若(-1)i(A0)i>0,∀1≤i≤n, 则f(x0)是极大值.
② det(A0)=0,rank(A)≤rank(A0)+1且A0所有主子式非负或者所有奇数阶主子式非正, 偶数阶主子式非负, 此时若A0的秩为k, 则极值点的全体构成了维数为n-k的空间, 其极值为
其中C0,detC0(C,detC)分别为选定A中r1,…,rk(r1,…,rk,n+1)行和列的主子矩阵和非零主子式(主子式), 1≤r1,…,rk≤n.若所有奇数阶主子式非正, 偶数阶主子式非负, 则极值是极大值; 若A0所有主子式非负, 则极值是极小值.
(ii)f(x)极值不存在当且仅当A0既非半正定也非半负定或者rank(A)≥rank(A0)+2.
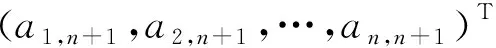
∇f=(fx1,fx2,…,fxn)=0,
即
或者用矩阵形式等价地
A0x0=-γn+1.
(i)若det(A0)≠0, 则由Cramer法则知
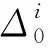
其中第二个等号是把第i列-γn+1移动到最后一列(先将第i列与第i+1列交换, 再将第i+1列与第i+2列交换,…, 将第n-1列与第n列交换)并把负号提到行列式外面并且利用了(-1)2i=1, 最后一个等号用到了A的代数余子式的定义.于是
其中第二个等号用到了临界点方程组, 第四个等号是利用Laplace展开定理对det(A)按n+1行展开, 并且注意到det(A0)=An+1,n+1.此时临界点和临界值分别为
(ii) 若det(A0)=0, 设A0的秩为k(不妨临设k≠0, 如果k等于零则A0=O, 这说明f(x)不是二次函数, 矛盾).可断言: 临界点方程组有解当且仅当rank(A)≤rank(A0)+1.事实上, 如果rank(A)≥rank(A0)+2, 记[A0,γn+1]和[A0,-γn+1]分别为
则
rank([A0,γn+1])≥rank(A)-1≥rank(A0)+1>rank(A0),
其中第一个不等式是因为矩阵A比矩阵[A0,γn+1]增加了一行, 而增加一行要么不改变秩, 要么秩增加1(这是线性代数中的一个结论, 即rank(A)≤rank([A0,γn+1])+1).第二个不等式是由假设rank(A)≥rank(A0)+2推得.这说明
rank(A0) 注意到 其中I为n阶单位阵.这说明 rank([A0,γn+1])=rank([A0,-γn+1]). 因此 rank(A0) 即临界点方程组系数矩阵的秩小于增广矩阵的秩, 由Cramer法则知临界点方程组无解.另一方面, 设rank(A)≤rank(A0)+1, 若rank(A0)≠rank([A0,γn+1]), 注意到[A0,γn+1]比A0多一列, 于是 rank(A0)+1=rank([A0,γn+1]), 记 A0=[γ1,…,γn],[A0,γn+1]=[γ1,…,γn,γn+1]. 则对任意的λ1,…,λn, 有 γn+1≠λ1γ1+…+λnγn. 同时转置可得 于是 这说明 rank(A)=rank([A0,γn+1])+1=rank(A0)+2, 这与假设矛盾.于是rank(A0)=rank([A0,γn+1]), 由Cramer法则知临界点方程组有解.这就证明了断言.因此只考虑rank(A)≤rank(A0)+1的情形, 由线性方程组的一般理论知其解构成了维数为n-k的空间.不失一般性, 不妨设其第1,2,…,k行和列对应的子式detC0不为零.按上述记号, 有 由Cramer法则可解得当1≤i≤k时, 的秩为k.事实上, 若不然, 设Mα的秩为k+1, 则临界点方程中有效方程组的个数必然大于等于k+1, 矛盾.对Mα的行列式使用Laplace展开定理, 和前面的计算类似有 其中第二个等号是合并同类项之后是i,j交换位置(因为最终的求和结果是与求和指标i,j无关的, 所以交换位置不影响求和的最终结果), 并且利用了对称矩阵的伴随矩阵仍然是对称矩阵的事实以及aαi=aiα.第三个等式是利用了上述detMα=0展开的结果和上述detC展开的结果.可断言:f(x0)与主子式非零对应的矩阵C0的选取无关.不失一般性, 不妨设另一个主子式非零的矩阵D0和对应的矩阵D为 注意到矩阵中如果存在线性相关的两个向量, 则其行列式必然为零.故不失一般性, 只需考虑第k+1行和第一行之间之间具有线性相关性, 即 (ak+1,1,ak+1,2,…,ak+1,n+1)=λ(a11,a12,…,a1,n+1). 注意到A的对称性 ak+1,k+1=λa1,k+1=λak+1,1=λ2a1,1,an+1,k+1=ak+1,n+1=λa1,n+1=λan+1,1. 于是有 其中第二个等号用到了A的对称性和第一行与第k+1行的线性相关性, 第三个等号是先将第k行的公因子λ和第k列的公因子λ提到行列式外面, 然后将第k行移动到了第一行(先将第k行与第k-1行互换位置, 再将第k-1行与第k-2行互换位置,…,第二行与第一行互换位置), 最后将第k列移动到了第一列(先将第k列与第k-1列互换位置, 再将第k-1列与第k-2列互换位置,…,第二列与第一列互换位置).通过上述类似的替换和行列变换有 即 这就证明了断言. 下面讨论极值的存在性与极大极小性: 令x=x0+x′,其中x0是某个固定的临界点.进一步计算得 其中λ1,λ2,…,λn是A0的所有特征值.则 ① 若rank(A)≥rank(A0)+2, 根据上面的讨论, 临界点方程组系数矩阵的秩小于增广矩阵的秩, 由Cramer法则知临界点方程无解, 故极值不存在; ② 若A0不是半正定或者半负定的, 该条件成立当且仅当λi是有正有负的.此时由f(x)-f(x0)表达式知极值不存在; ③ 若(A0)i>0,∀1≤i≤n或者(-1)i(A0)i>0,∀1≤i≤n, 该条件成立当且仅当A0的特征值全为正或者全为负.此时结合f(x)-f(x0)的表达知极值是存在唯一的.由上面的讨论知其极值点和极值分别为 显然若(A0)i>0,∀1≤i≤n, 则f(x0)是极小值; 若(-1)i(A0)i>0,∀1≤i≤n, 则A是极大值; ④ 若det(A0)=0,rank(A)≤rank(A0)+1且A0所有主子式非负或者所有奇数阶主子式非正, 偶数阶主子式非负, 该条件成立当且仅当A0非满秩, 临界点方程组有解且A0的所有特征值λi是非负或者非正.注意到A0≠O(否则f(x)不是二次函数), 这说明特征值不全为零.此时由f(x)-f(x0)的表达知极值是存在且唯一.而A0所有主子式非负当且仅当特征值非负, 此时极值是极小值.同理A0所有奇数阶主子式非正, 偶数阶主子式非负当且仅当特征值非正, 此时极值是极大值.若设A0的秩为k,C和C0的记号同上(并且容易验证此时是C0正定或者负定的), 则由上面的讨论知极值为 且极值点的全体构成了维数为n-k的空间. 作为定理的一个推论, 得到了关于二元二次函数的极值结果. 推论1设f(x,y)是上述形式的二元二次函数(A0≠O),则f(x,y)极值存在(且唯一)当且仅当下列情况之一成立: (i) det(A0)>0.此时其极值点和极值点分别为 并且若a11>0或者a22>0, 则f(x0,y0)是极小值;若a11<0或者a22<0, 则f(x0,y0)是极大值. (ii) det(A0)=0 且det(A)=0.此时极值点构成了二维平面上的一条直线.其极值为 并且若a11>0或者a22>0, 则极值为极小值; 若a11<0或者a22<0, 则极值为极大值. 解按照上述记号, 矩阵A为 显然det(A0)=det(A)=0, rank(A0)=2, rank(A)=3且A0的所有主子式均非负.注意到 3=rank(A)≤rank(A0)+1=2+1=3, 由定理1,f(x)的极小值存在.取第一行第二行, 第一列第二列构成的主子式对应的矩阵C0, 则直接的计算表明 detC0=2, detC=-3. 这说明极小值与主子式的选取无关. 解按上述记号, 矩阵A为 直接的计算表明 det(A0)=0, rank(A0)=2, det(A)=0, rank(A)=3. 并且A0的所有奇数阶主子式非正, 偶数阶主子式非负(即A0所有特征值非正), 并且 3=rank(A)≤rank(A0)+1=2+1=3, 根据定理1,f(x)存在极大值, 取第一行第二行, 第一列第二列构成的主子式对应的矩阵C0, 则直接的计算表明detC0=5, detC=-30.于是该极大值为f(x0)=-6,.事实上, 还可以验证与主子式的选取无关.取第二行第三行, 第二列第三列构成的主子式对应的矩阵D0, 则detD0=5,detD=-30; 取第一行第三行, 第一列第三列构成的主子式为E0, detE0=5,detE=-30.于是 这说明极大值与主子式的选取无关. 解按上述记号, 矩阵A为 直接的计算表明, det(A0)=22≠0,det(A)=-360.并且A0的所有顺序主子式均大于零, 由定理1可知f(x)存在极小值, 并且极小值点和极小值分别为 注 上述例子说明, 当A0是正定矩阵, 即使A不具有半正定性(注意到det(A)<0, 这说明特征值必有一个是负的, 因此不可能半正定),f(x)的极小值也是存在的. 解按上述记号, 矩阵A为 直接的计算表明, det(A0)=-11≠0, det(A)=44.并且A0的奇数阶顺序主子式小于0, 偶数阶顺序主子式大于0.由定理1可知f(x)存在极大值, 并且极大值点和极大值分别为 解按上述记号, 矩阵A为 直接的计算表明, det(A0)=-1<0, det(A)=0.并且A0所有一阶主子式为正, 二阶主子式为负.这说明A0既非半正定也非半负定.由定理1知,f(x)的极值是不存在的. 解按上述记号, 矩阵A为 直接的计算表明, det(A0)=0, rank(A0)=1, det(A)=-4, rank(A)=3.显然 rank(A)=3≥rank(A0)+2=3, 根据定理1,f(x)的极值是不存在的. 例7设f(x)=ax2+2bx+c为一元二次函数(a≠0), 求f(x)的极值. 解按上述记号, 矩阵A为 直接的计算表明, det(A0)=a≠0, rank(A0)=1, det(A)=ac-b2, 根据定理1,f(x)的极值存在且唯一.其极值点和极值分别为 并且a>0时f(x0)为极小值,a<0时f(x0)为极大值.这就从n元二次函数的极值问题的角度重新解释了一元二次函数的极值问题. 本文将n元二次函数求极值的公式化简为两个行列式的比值, 结果简洁且具有一般性(不受矩阵的秩的约束), 在实际应用中也非常方便. 致谢非常感谢本文审稿专家和编辑提出的宝贵的修改意见.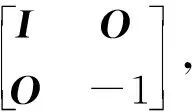

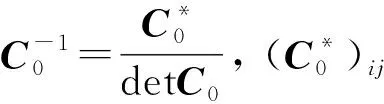

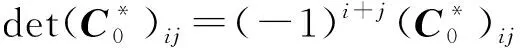
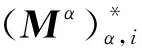
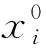
3 例 题
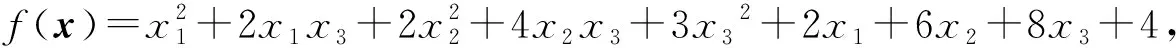
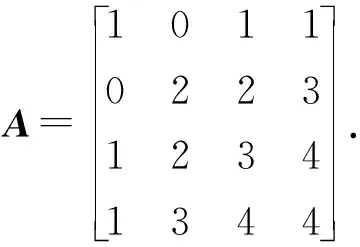
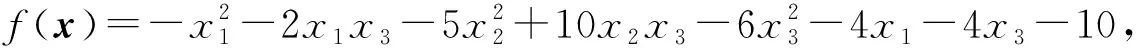
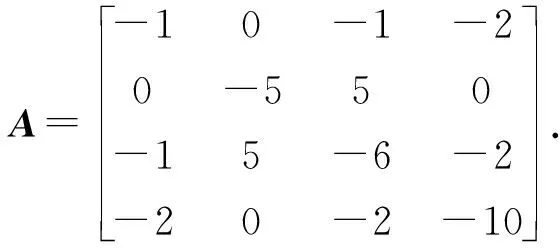

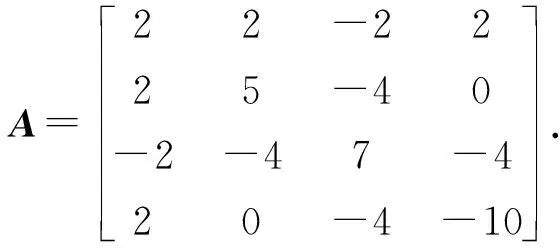
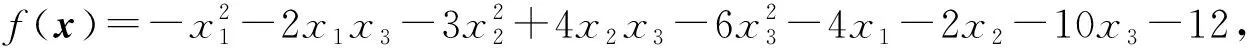
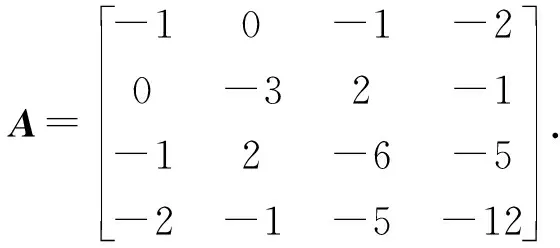
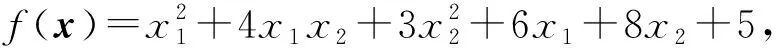

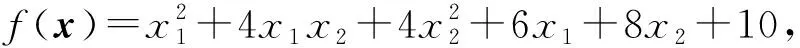
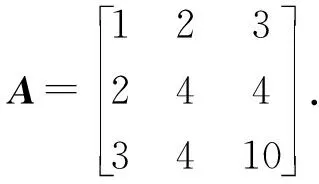
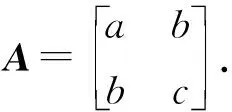
4 结 论

