协方差不等式的若干证明及其注记——兼论大学数学各学科教学的融合

欧阳顺湘

(哈尔滨工业大学(深圳)理学院， 广东深圳 518055)

1 引 言

数学是一个各方面高度融合的有机整体.如克莱因的名著《高观点下的初等数学》就体现了初等数学同高等数学的融合，数学各部分的融合，几何观念和算术观念的融合，感性与理性的融合等等[1].中国科学技术大学数学系曾开创“一条龙”教学法，把所有基础课综合为连续3年的一门课进行教学，并形成了分别以华罗庚、关肇直、吴文俊为“龙头”的教师团队：华龙、关龙和吴龙.这样做的目的就是为使学生对数学有一个整体的了解[2-3]. 但“一条龙”教学法对教师有很高的要求.传统上，大学数学各学科是分门别类各成系统讲授的，且各学科的教学又往往由不同的教师负责.在这样的客观条件下，需要任课教师关注各课程之间的联系，并在教学过程中主动融合其他学科.

作为教学融合的例子，笔者曾探讨将概率论方法应用于实分析中的问题[4]，将实分析中广泛使用的示性函数应用于初等概率论教学中[5]. 本文用十种不同但某些证明思想又相互关联的方法证明初等概率论中重要的协方差不等式，以进一步阐明概率论与分析、代数、几何以及数理统计等学科之间紧密的联系.笔者将另文考虑协方差不等式的多维推广，涉及格拉姆(Gram)矩阵、高维投影等内容，这也是对各学科教学相互融合的尝试.

记L2为概率空间(Ω，F，P)上所有二阶矩有限的随机变量组成的空间.对任意随机变量X，Y∈L2，用EX表示X的期望，用cov(X，Y)=E(X-EX)(Y-EY)表示X，Y的协方差，varX=cov(X，X)表示X的方差.如下协方差不等式是熟知的[6-10].

定理1设X，Y∈L2，则

(1)

且不等式(1)的等号成立当且仅当X，Y线性相关，即存在不全为零的常数a，b使得

P(aX+bY=c)=1，

其中c=aEX+bEY.

设随机变量X，Y的方差都不为0，则X，Y的相关系数ρ(X，Y)定义为

定理1表明|ρ(X，Y)|≤1，而该不等式中的等号成立意味着X，Y之间的相关系数为±1.

不等式(1)在概率论与数理统计中很重要，如可以用它证明Cramér-Rao不等式.形式上，不等式(1)与柯西-施瓦茨不等式、海森堡不确定性原理的方差描述非常类似.

柯西-施瓦茨不等式是经典不等式之一，在数学中有多种表现形式和各种应用[11].它的一般抽象形式如下：设(V，〈·，·〉)为内积空间，u，v∈V，则

(2)

且不等式(2)的等号成立当且仅当存在不全为零的常数a，b使得au+bv=0，即u，v线性相关.虽然L2上二元函数cov(·，·)具有正性、线性性和对称性，但它没有定性：cov(X，X)=0当且仅当X几乎处处等于常数，即P(X=EX)=1.因此cov(·，·)并不是L2上的内积，协方差不等式不是内积空间上柯西-施瓦茨不等式的直接推论.然而，cov(·，·)与内积的性质很类似.这暗示着协方差不等式与柯西-施瓦茨不等式有密切的联系.

本文将介绍十种证明定理1的方法(其中非直接应用柯西-施瓦茨不等式的证明都可用于证明柯西-施瓦茨不等式).有些证明不常见于初等概率论教材中.也介绍了构造二次函数、求极值等常见方法，目的是通过这些方法及其与其他方法的联系，说明这些常见方法的证明思想——这一点是不常见讨论的.

协方差不等式的各种证明用到了协方差的性质，应用了归一化、不相关化(类似于正交化)、构造二次型和二次函数、投影、恒等式、求极值等常见思想和方法，涉及商空间、内积空间及其几何的性质，展示了微积分、线性代数、几何、概率论与数理统计等学科之间的密切联系，由此可见数学的高度统一以及在大学数学教学中融合各学科的必要与方法.

2 预备知识

利用方差和协方差的性质，易得如下结论.该结论有利于更深入理解有线性关系的两个随机变量之间的关系.

引理1设X，Y∈L2且线性相关.如果varX≠0，则有如下结论：

(i) P(Y=αX+β)=1，其中

(ii) (1)中的等号成立；

定理1的证明可利用如下引理归结于部分情形的证明.

引理2设X，Y∈L2且varX≠0.为证定理1，只要证明

(3)

且不等式(3)的等号成立当且仅当

(4)

证在(3)中取Y为-Y可得

(5)

其中等号成立当且仅当在(4)中取Y为-Y仍成立：

(6)

综合(3)和(5)就得到

此即(1).注意到(3)和(5)的等号成立分别等价于

因此，(4)和(6)可统一表示为

即X，Y线性相关.

下面的结论也将用到.

引理3设X，Y∈L2，则存在常数t0∈，使得cov(X，Y-t0X)=0.

证若varX=0，则X几乎处处等于EX，因此对任何t∈，cov(X，Y-tX)=0.设varX≠0，取则

cov(X，Y-t0X)=cov(X，Y)-t0varX=0.

设varX≠0，varY≠0，将X，Y归一化为

3 协方差不等式的证明

下面将给出协方差不等式(即定理1)的十种证明方法.为简化叙述，将在多处用到如下事实.

可设varX≠0或varY≠0，否则不等式(1)两边同为0，因而自然成立，且此时X，Y显然线性相关.设varX≠0，如果X，Y线性相关，由引理1可知，不等式(1)中的等号显然成立.另一方面，根据引理2，为证明不等式(1)，实际上只要证明不等式(3)成立并存在常数α，β使得

P(Y=αX+β)=1.

上式又等价于var(Y-αX)=0.还可注意到存在常数a，b，c使得P(aX+bY=c)=1这一结论等价于存在常数a，b使得var(aX+bY)=0.

3.1 归一化方法

归一化方法是证明不等式的一种重要方法，它可以将求和转换为乘积.Hölder不等式的经典证明就是先利用Young不等式，再求和，然后用归一化方法[12].柯西-施瓦茨不等式是Hölder不等式的特例，自然也可以用归一化方法证明.受此启发，下面用归一化方法给出协方差不等式的证明.

证1由方差的非负性，有

var(X-Y)≥0.

(7)

因此

(8)

不妨设varX≠0且varY≠0.将(8)应用于

有

由此可得

(9)

注1 归一化方法很简洁，只需要灵活掌握方差的性质.该方法在分析中较为常见，如在[11]中就多次使用，但不常见有使用该方法证明协方差不等式的中文初等概率论教材.外文初等概率论(与数理统计)教材较多使用这个方法[8].

3.2 不相关化方法

人们利用格拉姆-施密特正交化程序将内积空间中的向量组正交化以得到标准正交基，进而用这个基来表示原来的向量.在L2中，也可以使用类似的想法，将随机变量“不相关化”.

显然varξ1=varξ2=1，ξ1和ξ2不相关，且有

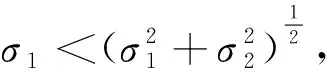
即(3)严格成立.

3.3 通过商空间直接应用内积形式柯西-施瓦茨不等式

经过问题转换，也可以直接应用柯西-施瓦茨不等式来证明定理1.

证3设

K={X∈L2∶存在常数c使得P(X=c)=1}.

则K为L2的子空间.对任意X，Y∈L2，如果X-Y∈K，则称X，Y等价.将与X等价的所有随机变量形成的类记为[X].由此可得商空间

L2/K∶={[X]∶X∈L2}.

在商空间上可以自然地定义加法、数乘和二元函数：对任意[X]，[Y]∈L2/K，a∈，

[X]+[Y]=[X+Y]，a[X]=[aX]， ([X]，[Y])〈[X]，[Y]〉K∶=cov(X，Y).

可以证明(L2/K，〈·，·〉K)为内积空间.从而由内积空间上的柯西-施瓦茨不等式(2)可得

等号成立当前仅当存在常数α∈使得[Y]=α[X].按商空间上内积的定义可得不等式(1)，而(1)的等号成立等价于Y-αX∈K，即存在常数β∈使得

P(Y=αX+β)=1.

3.4 应用柯西-施瓦茨不等式

将L2中任意两个几乎处处相等的随机变量看作同一个随机变量，或说将L2看作L2/K，其中N={X∈L2∶P(X=0)=1}.则L2上的二元函数(X，Y)EXY是L2上的内积. 类似于3.3中的程序，由(2)可得如下用期望表示的柯西-施瓦茨不等式:设X，Y∈L2，则

(EXY)2≤EX2EY2，

(10)

且不等式(10)的等号成立当且仅当存在不全为零常数a，b使得P(aX+bY=0)=1.利用这个结论，可以证明定理1.

证4将不等式(10)应用于X-EX，Y-EY，可得

[cov(X，Y)]2=[E(X-EX)(Y-EY)]2≤[E(X-EX)2][E(Y-EY)2]=varXvarY.

此即(1)，且上述不等式的等号成立当且仅当存在不全为零常数a，b使得

P(a(X-EX)+b(Y-EY)=0)=1.

即P(aX+bY=c)=1，且c=aEX+bEY.

注2 上述证明方法很自然，有些教材[6]即采用这种方法.

3.5 二次型方法

证5记X，Y的协方差矩阵为

对任何a，b∈，

可见Σ是非负定矩阵，从而Σ的行列式非负，detΣ≥0，即(1)成立.等号成立当且仅当存在不全为零的常数a，b使得(a，b)Σ(a，b)T=0，亦即var(aX+bY)=0.

3.6 二次函数方法

0≤var(aX+bY)=a2varX+2abcov(X，Y)+b2varY

=b2(t2varX-2tcov(X，Y)+varY)=b2var(Y-tX).

因此，设varX≠0，不妨考虑如下二次函数

tvar(Y-tX)=t2varX-2tcov(X，Y)+varY，t∈.

协方差不等式可由该函数的非负性经由判别式得到.这种构造二次函数的方法正是施瓦茨证明柯西-施瓦茨不等式的经典方法.

证6设varX≠0.考虑二次函数Q(t)∶=var(Y-tX)，t∈.有

Q(t)=t2varX-2tcov(X，Y)+varY.

因为对任意t∈，Q(t)≥0，所以Q(t)的判别式非正，

4(cov(X，Y))2-4varXvarY≤0.

这就证明了(1).该不等式的等号成立当且仅当存在某t0使得Q(t0)=var(Y-t0X)=0.

注3 也可以不用判别式而直接配方，

varXvarY-(cov(X，Y))2=Q(t0)varX.

(11)

因为Q(t0)≥0，可得(1).不等式等号成立当且仅当Q(t0)=0，即var(Y-t0X)=0.

注4 在微积分、线性代数中，该方法也常被用于证明离散形式、积分形式等各种不同形式的柯西-施瓦茨不等式.一些初等概率论教材[7，10]也使用该方法.教师应该注意到这个方法在教材中频繁出现的事实，提醒学生注意其普遍性.

3.7 投影法

类似于内积空间的几何思想，可以直观地如下理解：存在t0使得L2中三个随机变量X，Y-t0X，Y形成一个“直角三角形”(t0X为Y在X方向上的投影)，从而有“勾股定理”，

var(Y)=var((Y-t0X)+t0X)=var(Y-t0X)+var(t0X)，

并从中得到协方差不等式.这就引出如下方法.

证7设varX≠0，由引理3可知存在t0使得Y-t0X与X不相关.于是

(12)

因为var(Y-t0X)≥0，所以

由此可得(1)，且等号成立当且仅当var(Y-t0X)=0.

注5 由本方法可见证明6中的二次函数Q(t0)是“一条直角边”的长var(Y-t0X).

3.8 恒等式方法

设ai，bi∈，i=1，2，…，n，熟知有著名的格朗日恒等式

1773年，拉格朗日提出了n=3时的拉格朗日恒等式.古希腊亚历山大的丢番图曾写下n=2时的特例，而波斯数学家al-Khazin，意大利斐波那契，印度数学家婆罗摩笈多都曾得到n=2时的一般情形.从拉格朗日恒等式可以直接得到实数情形的柯西-施瓦茨不等式

且等号成立当且仅当对任意i，j=1，2，…，n，aibj-ajbi=0，即数组(a1，a2，…，an)与(b1，b2，…，bn)成比例.受此启发，有类似的方法证明协方差不等式.

证8设varX≠0，则(参(11)或(12))

从该等式可以直接得到协方差不等式及等号成立的条件.

3.9 极值法：最小方差

证9设varX≠0，因为

由此可得(1)，且(1)中等号成立当且仅当var(Y-t0X)=0.

3.10 极值法：最佳线性逼近

设ξ∈L2，s∈，则

E(ξ-s)2=varξ+(Eξ-s)2.

证10设varX≠0，θ(s，t)∶=E(Y-s-tX)2.对θ(s，t)分别关于s，t求偏导数并令偏导数为0，有

(13)

解方程可得

因此有

由此可得(1)，且等号成立当且仅当P(Y=s0+t0X)=1.

注6 该方法的思想是用线性函数s+tX逼近Y，使s+tX与Y的均方误差最小.因此，将s0+t0X称为Y的最小线性二乘逼近.这是统计学中最小二乘法、一元线性回归的思想.其思想也可理解为在单位元与X张成的线性空间span{1，X}中寻求Y的最佳逼近s+tX，系数s，t应该使得Y-s-tX与span{1，X}不相关(粗略地说，即几何意义下的“垂直”)，为此只要Y-(s+tX)分别与1和X不相关即可.它们分别为(13)中求偏导数所得的两个等式

E(Y-s-tX)·1=0， E(Y-s-tX)X=0.

的意义.

注7 该证明方法也常见于教材[9].这个思想可以推广到高维，即考虑多个随机变量向多个随机变量张成的空间的投影.它与多元线性回归密切相关.甚至可以进一步思考，如何用X的可测函数(不一定为线性函数)来逼近Y？高等概率论将给出答案，Y关于X的条件期望与Y的均方误最小.这就可以激发学生对高等概率论课程的兴趣.

4 结 论

通过展示协方差不等式的不同的证明，学生可以更好地掌握协方差的性质，联系到大学数学其他课程中的内容，掌握数学中常用数学思想和方法，认识到数学的统一性.怎样在分科教学的环境下促进教学的融合呢？徐利治曾回忆他在吉林大学数学系教了十七门不同的数学课程，增长了很多知识；他还提倡他的研究生多教不同课，扩大兴趣，提高水平.他认为这样可以教学相长[13].教师水平提高了，对教学融合自然有利.因此，大学教师可以考虑不要在较长时间内只担任一两门相同课程的教学.

致谢作者非常感谢相关文献，特别是[8]对本文的启发.由笔者完成的[8]的中译本即将由高等教育出版社出版.