序列(12+Q)(22+Q)…(n2+Q)中的完全平方数
张庆杰,牛传择
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
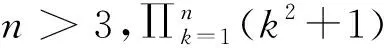
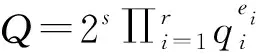
定理1存在某个与Q相关的正整数NQ,使得当n≥NQ时,Sn不是完全平方数。
显然,在得到NQ的值后,对n Sn的完全平方性与其素因子的次数相关,在本节中,我们从Sn的素因子入手,给出相关引理和命题。 引理1设Q<3n2,若有理素数p满足p2|Sn,则p<2n。 证由于p2|Sn,存在以下两种可能: (2) 若p|k2+Q且p|j2+Q,其中1 (1) (2) 易知,Sn>(n!)2,故有 (3) 引理3[14]若a为奇数且e∈*,则x2≡a(mod2e)有N个解,其中 (4) 证考虑同余方程 x2≡-Q(mod2j)。 (5) (1)Q为奇数。由引理3,当j=1时,(5)仅有一解;当j=2及-Q≡1(mod4)时,(5)恰有2解;当j≥3及-Q≡1(mod8),(5)恰有4解;其它情况下,(5)无解。故由(1)可得 t2≡-Q1(mod2j-s)。 (6) ≤B(n,Q)。 命题得证。 x2≡-qeQq(modqj)。 (7) 因此, 命题得证。 在本节中,我们利用上述引理和命题,给出定理1的证明。 由(3)可得 (8) 结合引理4,由(8)得 (9) 由(4)知当p>n时,αp≤2,所以根据引理5及(9),可得 (10) 又由(2)得 所以 (11) 因此,当n>1时,由(10)、(11)与引理6得 由命题1及命题2,当Q为奇数,即s=0时, (12) 当Q为偶数,即s>0时, (13) 当n→∞时,(12)、(13)右端的极限分别为 (14) (15) 在本节中,我们以Q=2,5为例,给出确定Sn完全平方性的方法。 接下来,讨论n<2818163的情况。显然,S1=3,S2=2×32,S8=24×39×112×17×19均不是完全平方数。 (1)a3=32+2=11,若ord11(Sn)≥2,则n≥11-3=8,易知Sn中第二次出现素因子11的项为a8,故当3≤n≤7时,Sn不是完全平方数。 (2)a9=92+2=83, 若ord83(Sn)≥2,则n≥83-9=74,易知a74第二次出现素因子83,故当9≤n≤73时,Sn不是完全平方数。 (3)a57=572+2=3251, 若ord3251(Sn)≥2,则n≥3251-57=3194,易知a3194第二次出现素因子3251,故当57≤n≤3193时,Sn不是完全平方数。 (4)a1683=16832+2=2832491, 若ord2832491(Sn)≥2,则n≥2832491-1683=2830808,易知a2830808第二次出现素因子2832491,故当1683≤n≤2830807时,Sn不是完全平方数。 综上,Sn均不是完全平方数。 接下来,讨论n<13553819的情况。显然,S4=22×34×72为完全平方数,而S1=2×3,S2=2×33,S3=22×33×7,S5=23×35×5×72不是完全平方数。 (1)a6=62+5=41,若ord41(Sn)≥2,则n≥41-6=35,易知a35第二次出现素因子41,故当6≤n≤34时,Sn不是完全平方数。 (2)a12=122+5=149, 若ord149(Sn)≥2,则n≥149-12=137,易知a137第二次出现素因子149,故当12≤n≤136时,Sn不是完全平方数。 (3)a126=1262+5=15881, 若ord15881(Sn)≥2,则n≥15881-126=15755,易知a15755第二次出现素因子15881,故当126≤n≤15754时,Sn不是完全平方数。 (4)a3744=37442+5=14017541, 若ord14017541(Sn)≥2,则n≥14017541-3744=14013797,易知a14013797第二次出现素因子14017541,故当3744≤n≤14013796时,Sn不是完全平方数。 综上,Sn为完全平方数当且仅当n=4。 类似地,对于任意给定的正整数Q,均可确定Sn的完全平方性。利用以上方法,确定1≤Q≤100时Sn的完全平方性如下:若Q∈{1,11,23},则Sn为完全平方数当且仅当n=3;若Q∈{3,8,15,24,35,48,63,80,99},则Sn为完全平方数当且仅当n=1;若Q=5,则Sn为完全平方数当且仅当n=4;若Q∈{x|1≤x≤100且x∈}{1,3,5,8,11,15,23,24,35,48,63,80,99},则Sn均不是完全平方数。 我们猜想:当Q≥24时,Sn是完全平方数的充要条件为Q+1为平方数且n=1。 本文就Sn是否为完全平方数进行了研究,将Cilleruelo[2]讨论的Q=1和陈红[6]讨论的Q=23推广至一般的正整数Q。首先利用反证法证明了定理1这个一般性结论,接下来以Q=2,5为例给出了确定Sn完全平方性的方法,利用此方法,对于任意给定的正整数Q,Sn的完全平方性均可确定。
1 主要引理和命题
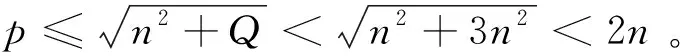
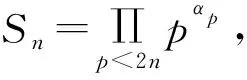
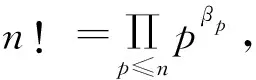
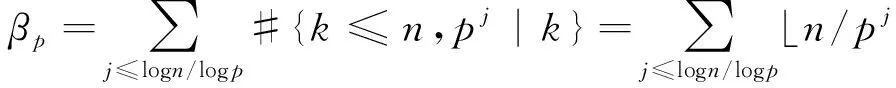
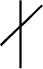
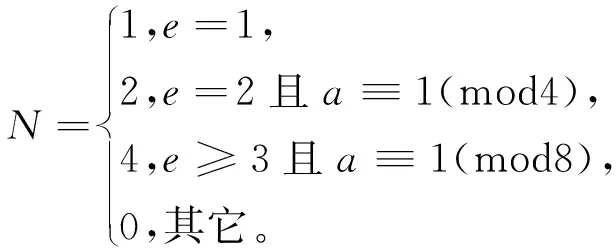
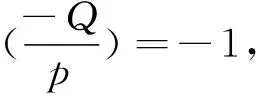
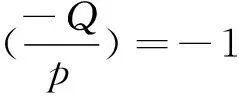
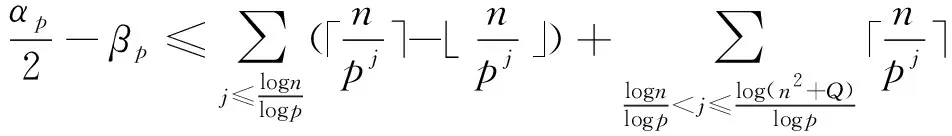
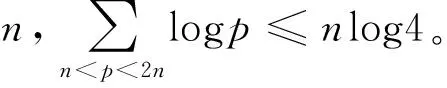
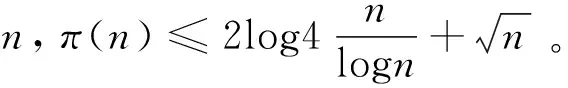
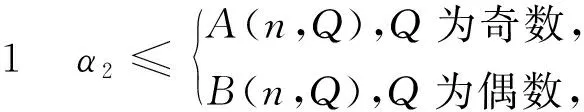


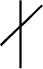
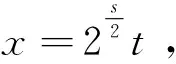
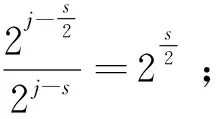

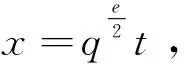
2 定理的证明
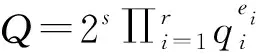
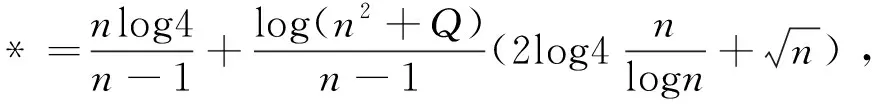
3 Sn的完全平方性
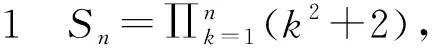
4 结论

