基于C1型Bell三角形单元的挠曲电效应分析
庄晓莹,李 彬
(同济大学土木工程学院,上海 200092)
力电耦合效应广泛存在与各种材料之中,包括人工和天然材料。自然界的很多生物功能都是力电耦合的,如听觉感知、与动作有关的神经元突起等。这些现象激发了对此相关机理的研究,并开发可以模仿它们的新材料。在所有力电耦合效应中,研究最多的就是压电效应,它是应变和极化之间的力电耦合效应。

式中:pi是电极化;eijk为三阶压电系数;εjk为应变。压电效应是由晶体内原子的相对位移引起的,只存在于非中心对称晶体中。
不同于压电效应的应变与极化的耦合,挠曲电效应是应变梯度与极化或者应变与极化梯度的耦合。

式中:fijkl为四阶挠曲电系数;ηjkl为高阶应变。挠曲电效应产生的原因是晶体材料局部对称性的变化。传统宏观尺度上应变梯度较小,挠曲电效应可以忽略不计,但在微纳尺度上结构可以产生很大的应变梯度,使得挠曲电效应在纳米尺度上和压电效应相当。挠曲电效应存在于所有晶体类型中,并在超过居里温度时仍然出现。相比压电效应,挠曲电效应更为普遍,而且它还能产生压电不具备的其他力电功能,关于挠曲电效应理论及相关应用可见以下文献综述[1-7]。
固体材料结构随着特征尺度的减小表现出明显的尺度效应,但经典连续介质力学本构关系中不包含任何尺度参量,无法描述微构件力学性能的尺寸效应,因此需要引入长度标度,如梯度弹性理论。Mindlin在1965年提出了一个梯度弹性理论[8],该理论中,应变能密度被认为是应变和一阶、二阶应变梯度的函数,从而应力σ、应变ε的本构关系可以写成[9]:
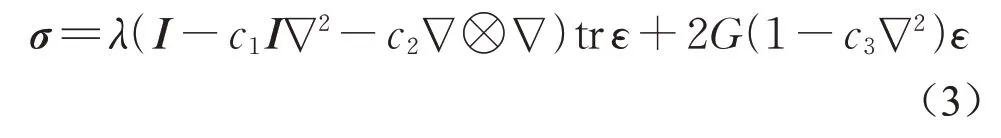
式中:c1、c2、c3是三个具有长度平方量纲的独立梯度参数;λ和G为Lamé常数;I为单位张量;∇为微分算子;∇2为拉普拉斯算子;tr为迹运算;⊗为张量积运算。当c2=0,c1=c3=l2时,式(3)就是在挠曲电效应分析中常见的拉普拉斯型梯度弹性本构方程:
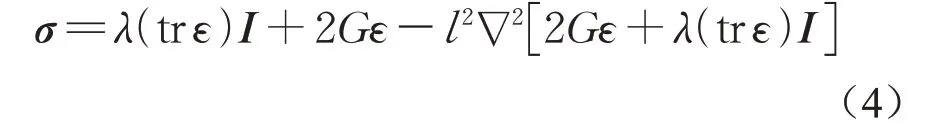
式中:l即为材料单参数的内禀尺度。由于挠曲电效应中涉及应变梯度,要求插值函数至少C1连续,传统的有限元方法采用拉格朗日插值往往仅具备C0连续。常见的应用于挠曲电效应分析的方法有混合有限元方法[10-11]、无网格方法[12-13]、等几何方法[14-15]。混合有限元方法中,位移和位移导数是相互独立的变量,它们的运动学关系需要额外的自由度施加约束,从而使得格式较为复杂。对于无网格方法和等几何方法,它们不是插值类型的单元,因此不容易处理复杂的边界条件,在商用软件中也不容易扩展。C1型有限单元开始用于平板的受弯分析,相关学者开发了一系列的C1型有限单元[16],其中Argyris三角形单元也用于挠曲电效应的分析[17],但对于C1型有限单元在挠曲电效应分析的研究还很少。
本文主要研究Bell三角形单元,它是由Argyris单元简化而来,其节点自由度包含位移及全部的一阶和二阶导数,Bell单元已经被用于许多梯度弹性问题的求解[18-20]。基于梯度弹性理论,给出了Bell单元分析挠曲电效应的一般格式,并通过数值算例验证了Bell单元的准确性和收敛性,分析了内禀尺度对结构变形的影响。此外,利用挠曲电结构的非对称性设计压电结构,阐述了相关原理,并说明了挠曲电的尺寸效应。
1 挠曲电效应
不考虑压电效应,对于各向同性挠曲电材料,电焓密度H[10]可以表示为
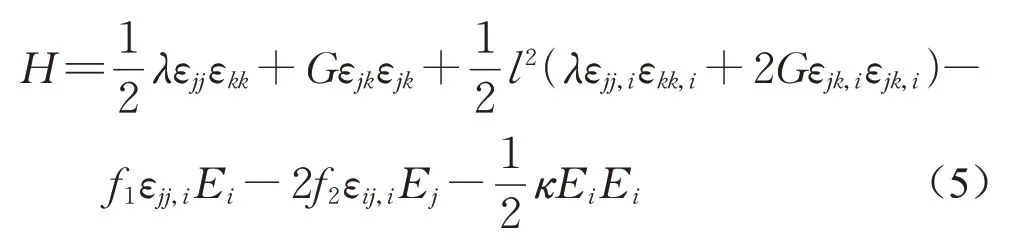
式中:εij为应变,定义为其中u为位移;Ei为电场强度,定义为Ei=-ϕ,i,其中ϕ为电势;f1和f2为挠曲电材料两个相互独立的系数;κ为介电系数;l为材料内禀长度,它在梯度弹性理论(式(4))中引入。
本构方程可表示为
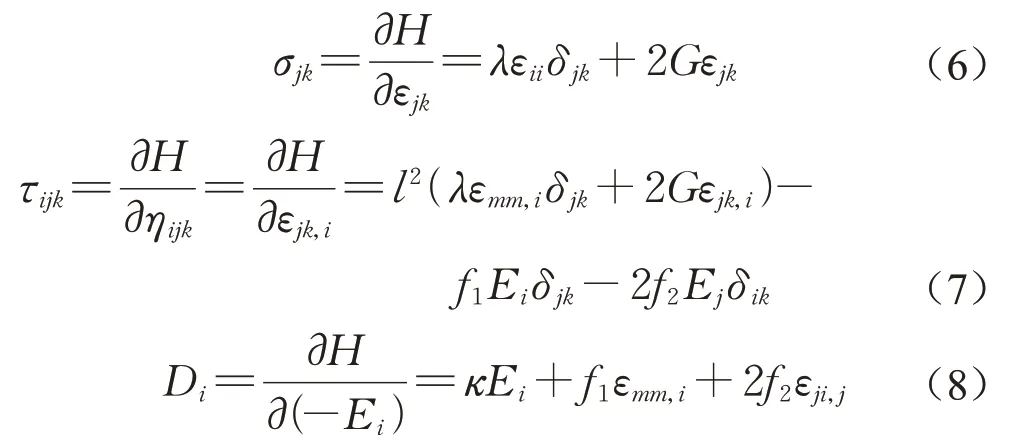
式中:σjk为应力;τijk为高阶应力;Di为电位移;ηijk为高阶应变,定义为ηijk=εjk,i。
平衡方程可推得:
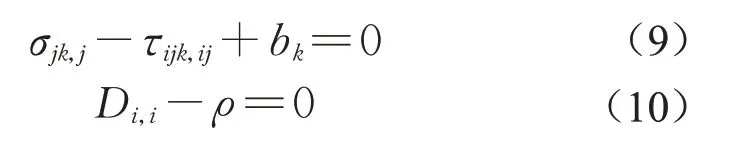
式中:bk为体积力;ρ为体自由电荷。
2 C1型三角形单元
Argyris三角形单元(图1)和Bell三角形单元(图2)是两种重要的C1型三角形单元。对于Argyris单元,单元自由度包括节点位移w及其一阶、二阶导数,以及三边中点法向导数。位移插值为五次函数,边界上的法向导数插值为四次函数。然而,边中节点法向导数自由度会显著增大单元刚度矩阵的带宽,这三个自由度可通过角节点的位移导数消去,即为Bell单元。对于Bell单元,位移的插值依然是五次函数,而边界上的法向导数插值变为三次函数。挠曲电效应是四阶偏微分方程问题,故Argyris和Bell单元均满足完备性和协调性要求,当划分单元足够小,有限元解趋近于精确解。
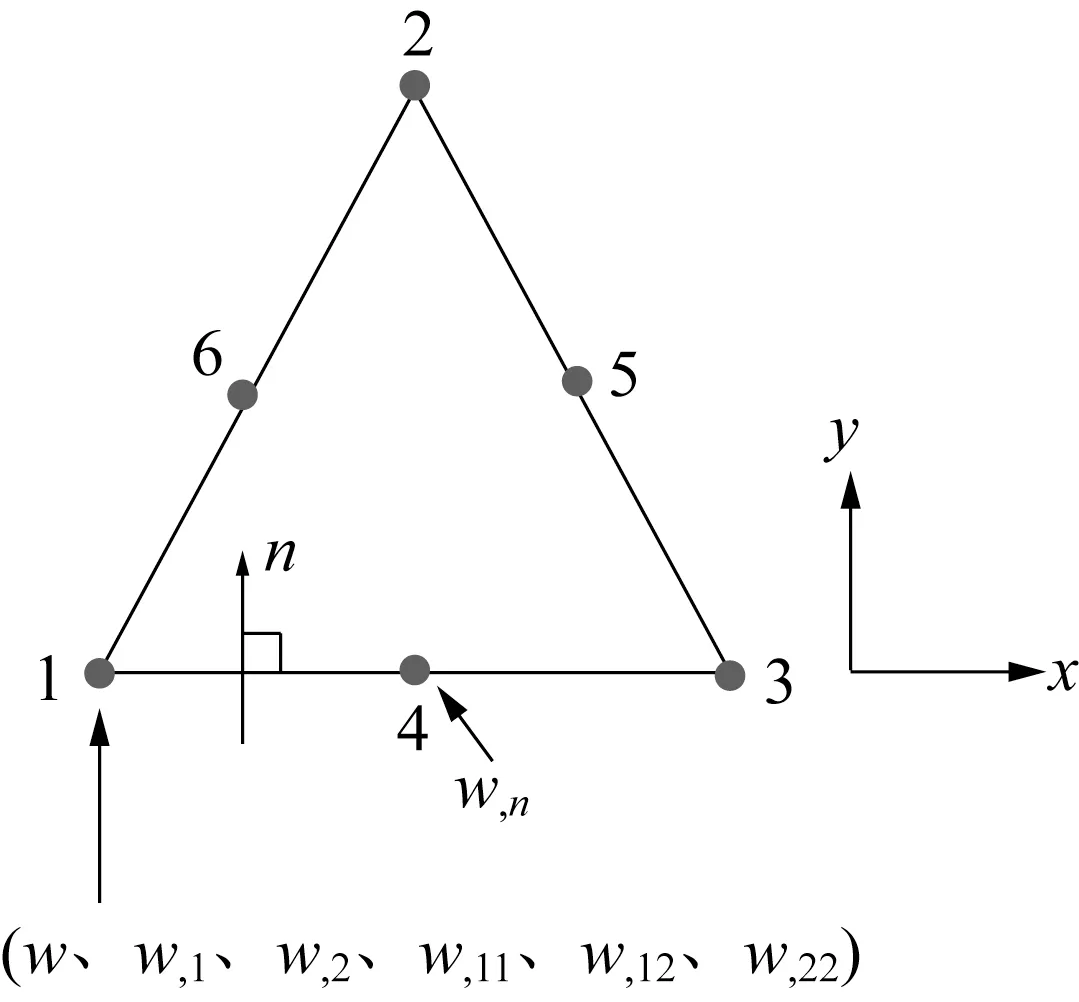
图1 Argyris三角形单元Fig.1 Argyris triangle element

图2 Bell三角形单元Fig.2 Bell triangle element
Bell三角形单元是基于插值函数的协调单元,便于建模和施加复杂的边界条件,也很容易在商用软件中扩展。对于挠曲电效应分析,Bell单元每个节点有18个自由度,分别是位移、电势以及它们的一阶、二阶导数。
挠曲电效应弱形式可表达为

式中:b、t、ρ和ω分别为体积力、面积力、体自由电荷和表面电荷密度。
离散后,单元内部的位移场和电势场可表示为

式(12)中:ve和φe分别为单元节点位移和电势;Nu和Nϕ分别为单元位移和电势形函数,定义为
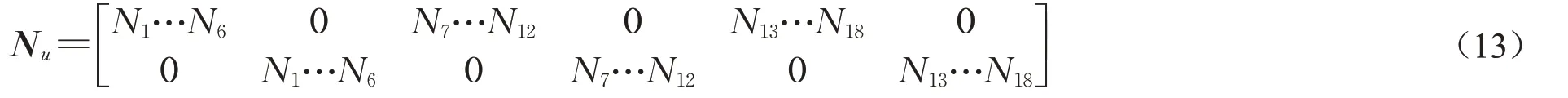
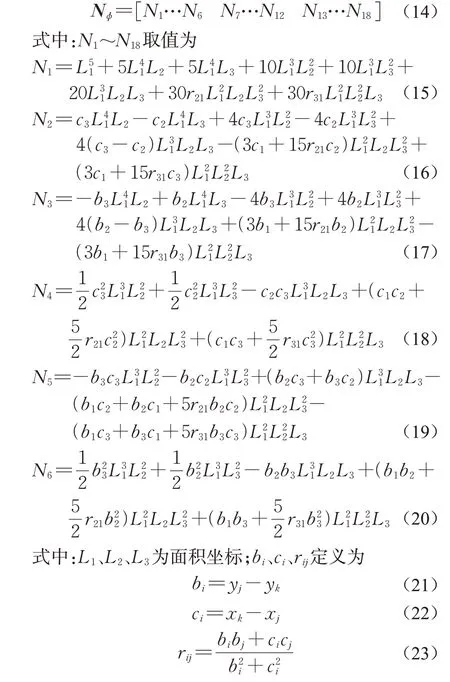
式中:xj和yj为坐标值;i、j、k的取值采用指标轮换,即1→2,2→3,3→1。N7~N18的取值也采用同样的指标轮换。
应变ε、高阶应变η及电场E的取值为ε=(ε11ε222ε12)T,η=(η111η1222η112η211η2222η212)T,E=(E1E2)T,可计算为

式中:Bu、Hu和Bϕ分别为位移形函数的梯度矩阵、海森矩阵和电势形函数的梯度矩阵。
将式(12)和(24)代入弱形式方程(11),可得如下单元节点平衡方程:
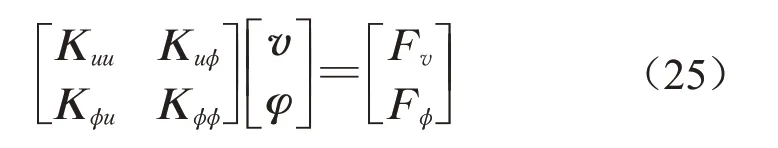
式中:v和φ分别为结构整体位移和电势;结构整体耦合刚度矩阵和节点载荷矩阵表达为
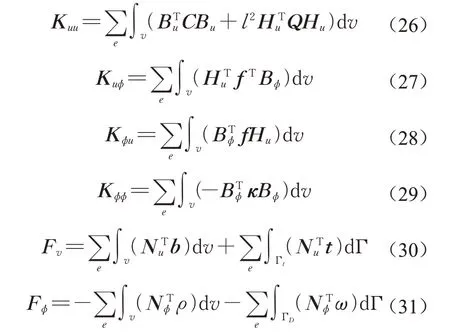
式中:材料参数C、Q、f、κ所对应的矩阵为

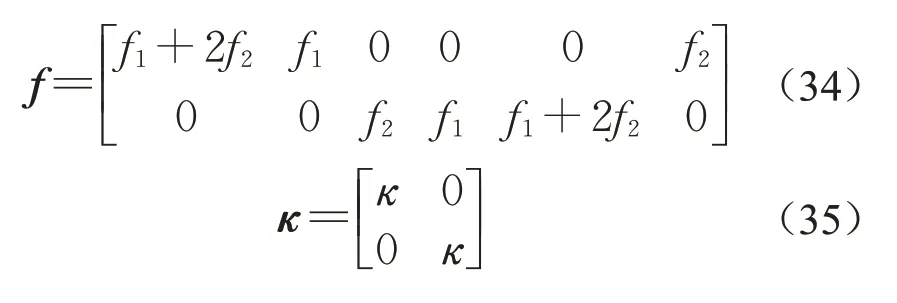
3 算例
Bell三角形单元通过Abaqus用户单元子程序UEL实现,采用TECPLOT进行结果的后处理。本文首先通过厚壁筒内外表面受压下变形的数值解与理论值的对比,验证Bell单元的准确性,讨论内禀尺度对结果的影响。然后,利用挠曲电结构的非对称性设计产生压电效应,并研究挠曲电的尺寸效应。
3.1 厚壁筒平面应变问题
图3为一厚壁筒,它的内径r0为10 μm,外径r1为20 μm,其受到内外表面电势差1.0 V作用。此外,内外径施加指定的位移载荷,内径位移ur0为0.045 μm,外径位移ur1为0.05 μm,挠曲电材料参数取值参照文献[10],见表1。

图3 厚壁筒模型Fig.3 Model of cylinder
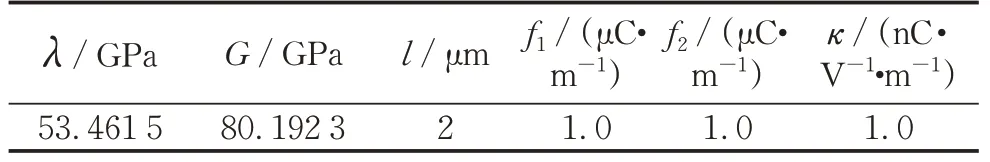
表1 挠曲电材料参数Tab.1 Material properties of flexoelectricity
不考虑体自由电荷,将本构方程(6)—(8)代入平衡方程(9)、(10),可得:
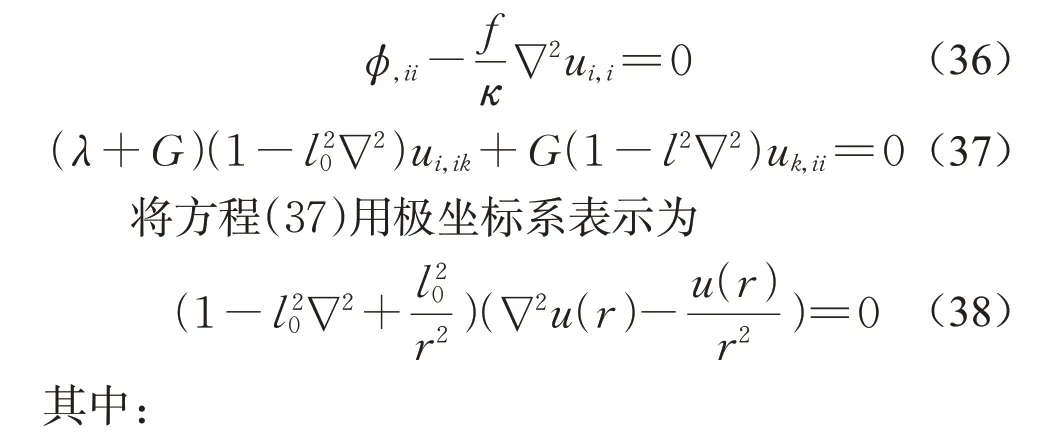

由于厚壁筒结构的对称性,位移和电势只与半径有关,方程(38)的解可表示为[10-11]
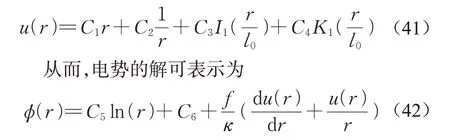
其中:I1和K1为一阶修正的第一类和第二类贝塞尔(Bessel)函数,方程(41)和(42)有C1~C6共6个未知数,可以通过如下6个边界条件求得:
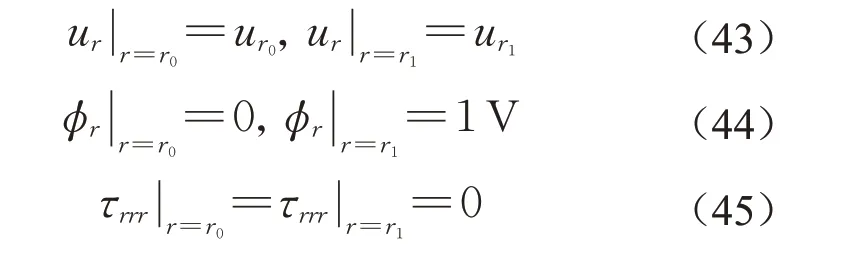
厚壁筒的切向位移和电势均为零,沿筒壁厚度方向径向位移的理论解以及不同网格密度的数值解见图4。对于比较稀疏的网格(环向48个单元,径向5个单元),数值解也与理论解吻合得很好。呈环状的位移云图也反映了位移仅与半径有关。图5为不同网格密度下,径向位移数值解与理论解误差绝对值的对数坐标图(两端点由于施加位移约束,误差过小,因此略去)。总体来讲,随着网格密度的增加,数值解与理论解的误差减少。当网格比较稀疏,误差在对数坐标下的曲线呈现比较明显的振荡。径向网格数量为20和40的误差曲线大致重合。图6为筒壁厚度方向电势的理论解和数值解对比,稀疏网格会造成数值解与理论值略有偏差,当径向网格数量为20时,数值解与理论值位移曲线几乎重合。图7为不同网格密度下,径向电势数值解与理论解误差绝对值的对数坐标图(端点值略去)。随着网格的加密,误差同样减少,当径向网格数量加密到20时,误差曲线已较为光滑,数值解收敛。从图5和图7中可以看出,此时径向位移和电势数值解与理论解的误差绝对值分别小于10-5μm和10-2V。位移和电势的数值解与理论值对比说明了Bell三角形单元的准确性与解的收敛性。

图4 位移ur的理论解和不同网格密度的数值解Fig.4 Theory solution and numerical solutions of different mesh grids of ur

图5 位移ur的理论解和不同网格密度的数值解误差绝对值Fig.5 Absolute value of ur error between theory solution and numerical solutions of different mesh grids
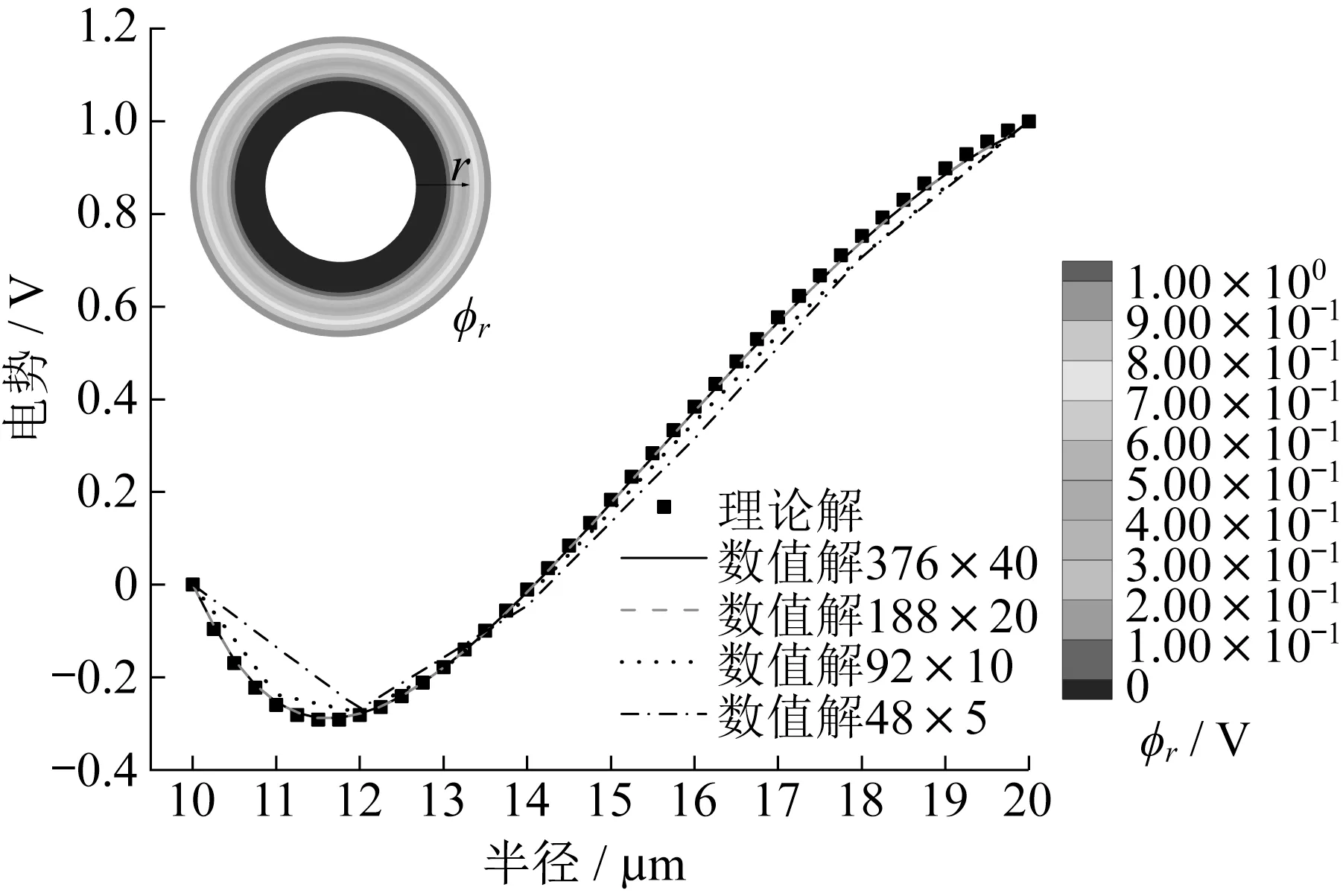
图6 电势ϕr的理论解和不同网格密度的数值解Fig.6 Theory solution and numerical solutions of different mesh grids of ϕr

图7 电势ϕr的理论解和不同网格密度的数值解误差绝对值Fig.7 Absolute value of ϕr error between theory solution and numerical solutions of different mesh grids
材料的内禀尺度l对径向位移的影响见图8,网格密度设为188×20,即环向188个单元,径向20个单元。从图中可以看出,数值解同样与理论解完全重合。此外,内禀尺度l越小,径向位移曲线弯曲程度越大,即径向应变(∂ur/∂r)的梯度越大,这也可以从图9中更直观地看出。材料系数Q反映了高阶应力与高阶应变的关系,其表达式中含有内禀尺度的平方项,因此较大的内禀尺度会减小结构的应变梯度。在挠曲电材料计算中,内禀尺度大都直接设定,其取值方法需要进一步研究。
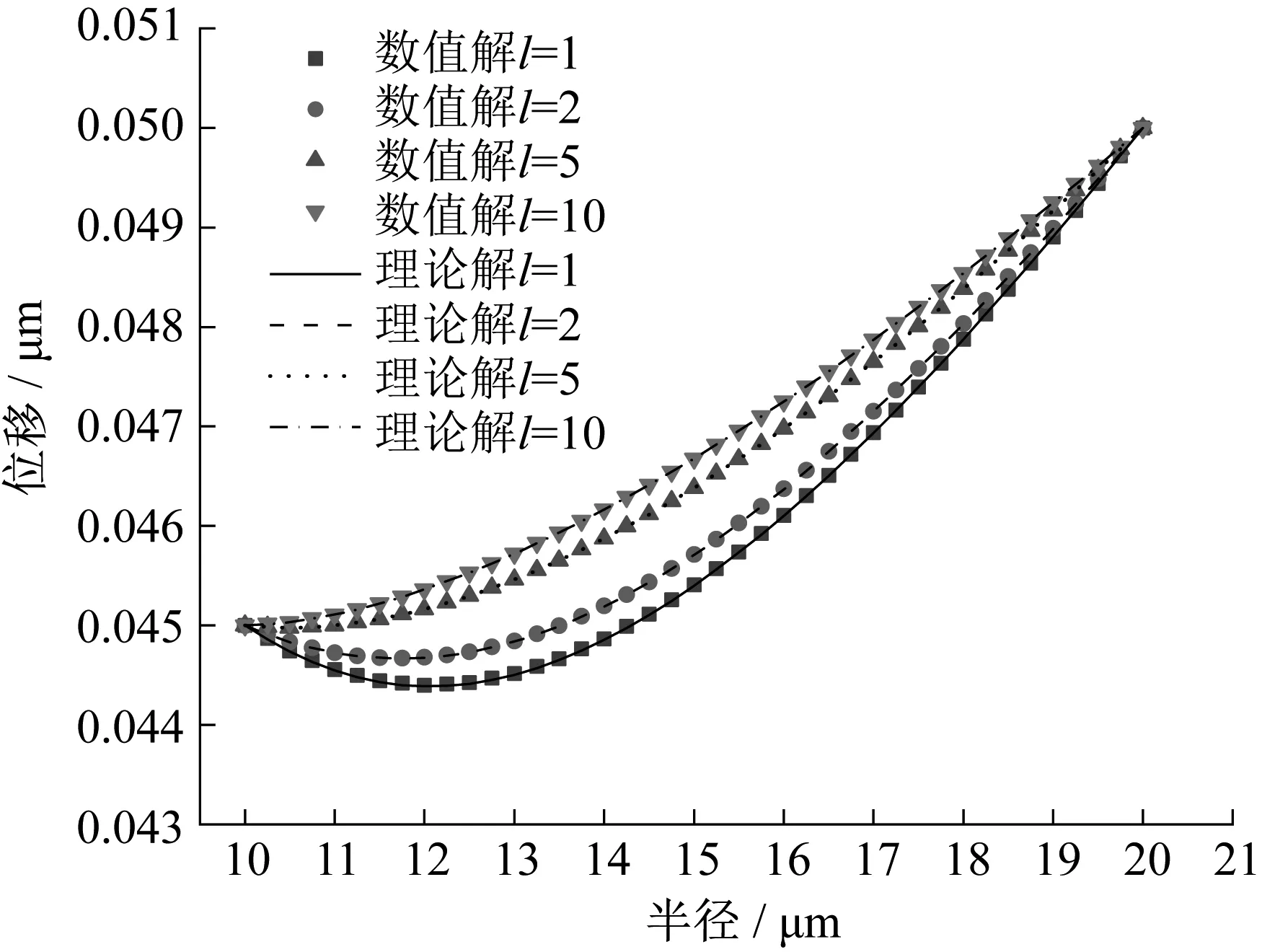
图8 不同内禀尺度下的位移ur的解Fig.8 Solutions of ur for different intrinsic lengths
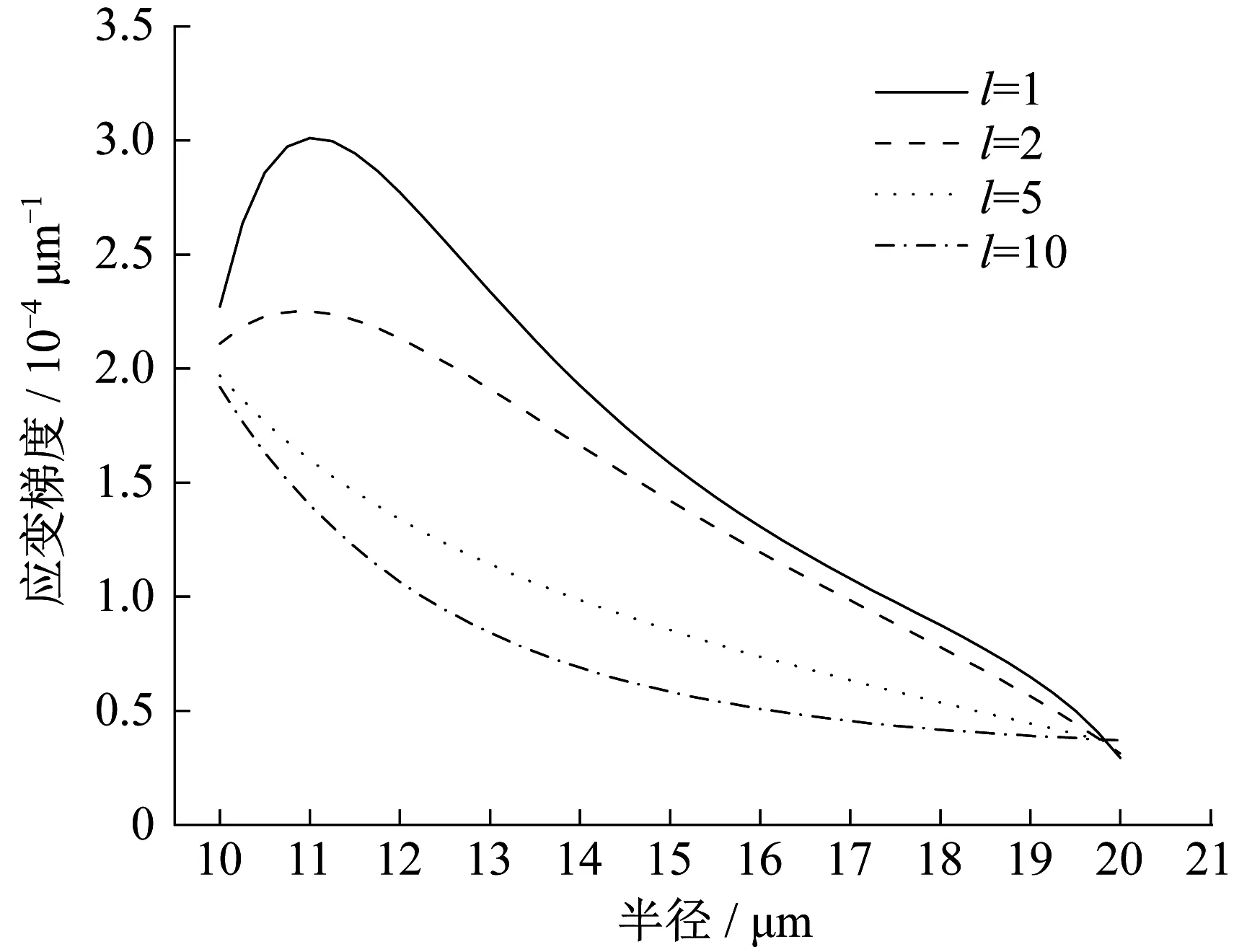
图9 不同内禀尺度下的应变梯度ur''Fig.9 Strain gradient ur''for different intrinsic lengths
3.2 利用挠曲电材料结构的非对称性产生压电效应
相比压电材料,挠曲电效应存在于所有电介质中,而且不受居里温度的限制。挠曲电效应的一个重要应用就是利用挠曲电材料(非压电材料)设计结构产生压电效应[21-22]。在正方形中心开孔,当受到均匀拉力时,结构内部由于应力分布不均匀就会产生应变梯度。但如果开孔是上下左右均对称,如圆形等,结构的平均电极化仍为零。因此,产生非零电极化需要利用开孔的不对称性,如图10所示的三角形结构。结构边长S为1 μm,开孔三角形的内接圆半径r为0.4 μm,左边位移和电势均为零,右边施加1.02×10-4N·μm-1的线荷载F,此问题设为平面应变问题。
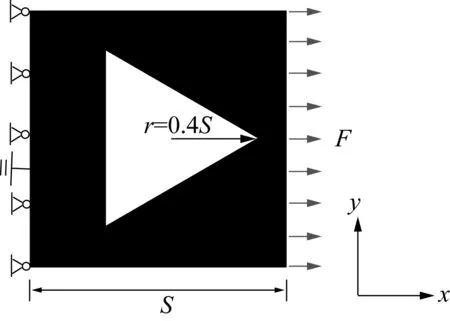
图10 三角形开孔的正方形结构Fig.10 Square structure with a triangular hole
不同内禀尺度下,结构右边电位移D1(水平方向)如图11所示。由于结构的对称性,电位移曲线沿y=0.5 μm轴对称。当内禀尺度较大时,电位移很小,而当内禀尺度较小时,电位移则比较显著,这是由于较大的内禀尺度减弱了结构的应变梯度。右侧电位移D2(竖直方向)如图12所示,此时电位移曲线沿中轴反对称,电位移D2沿边线的积分为零。由于结构是上下对称、左右非对称的,电位移才会出现上述的对称和反对称性,这也说明了开孔需是非对称的才可以产生压电效应。与图11类似,当内禀尺度较小时,结构中会产生更大的应变梯度,电位移D2会更为显著。挠曲电材料一个重要特点是尺寸效应,即挠曲电效应在小的尺度下尤为显著。对于许多材料,挠曲电系数很小,但在纳米尺度下,挠曲电效应非常强,而不能忽略。当逐渐缩小结构边长S,由微米尺度到纳米尺度(内禀尺度和荷载以相同比例缩小),结构的电位移D1如图13所示。随着结构尺寸的减小,结构电位移随之增大。结构尺寸每减小10倍,电位移相应增大10倍左右。这一特点有利于微纳尺度下挠曲电材料结构设计。
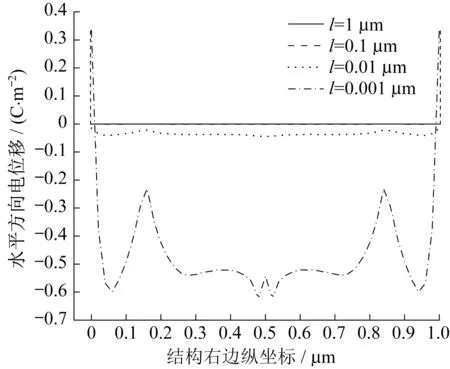
图11 不同内禀尺度下的电位移D1Fig.11 Electric displacement D1 for different intrinsic lengths

图12 不同内禀尺度下的电位移D2Fig.12 Electric displacement D2 for different intrinsic lengths

图13 不同结构大小的电位移D1Fig.13 Electric displacement D1 for different structure sizes
4 结语
本文基于Bell三角形单元进行了挠曲电效应的分析。Bell三角形单元是C1型协调单元,便于处理复杂边界条件,也很容易在商用软件中扩展。给出了在挠曲电分析中Bell单元的一般格式,并在数值算例中验证了它的准确性和收敛性。梯度弹性理论中引入的内禀尺度,可以用来预测微小尺度材料和结构中的尺度效应。较大的内禀尺度会减小结构的应变梯度,减弱正向挠曲电效应产生的电位移。此外,本文还利用结构的非对称性产生压电效应,通过电位移的分布阐述了相应的原理。挠曲电效应会随着结构尺度的减小显著增大,这有利于其在微纳尺度中的应用。
Bell三角形单元的一个劣势是其节点自由度较多,另外它扩展到三维单元还存在一定难度。本文采用了单参数的内禀尺度,其取值大都直接给出,此外还有学者采用多个内禀尺度参数进行挠曲电效应的分析[23]。Bell单元的计算效率、扩展问题,以及内禀尺度的选取,都需要进一步研究。
作者贡献声明:
庄晓莹:学术指导,研究方法,撰写论文,论文修改。李彬:理论推导,数值计算,撰写论文。

