基于粒子群算法的SWMM参数多目标率定研究

张 建，杜 尧，周正模，许树洪

(1.江苏省镇江市京口区水利局，江苏 镇江 212000；2.河海大学水文水资源学院，江苏 南京 210024)

1 概述

快速的城市化和极端气候变化导致城市流域内涝频发，严重威胁了人民生命财产安全和社会经济的可持续发展[1]。数值模拟是研究城市内涝过程，解决城市内涝问题的重要手段之一，其中SWMM模型因其出色的水文、水动力计算性能应用最为广泛[2- 3]。为保障SWMM模型对洪涝过程的模拟精度，准确地率定模型参数至关重要。传统的模型参数率定由建模人员凭借自身经验人为决定，但这种方法耗时耗力。为了提高效率和准确性，智能搜索算法开始被应用于模型参数率定工作中。粒子群算法凭借其算法规则简单，收敛速度快的特点，成为模型参数率定中最为广泛应用的算法之一[4- 5]。然而，参数率定结果的准确性，不仅取决于采用的搜索算法，还受率定目标函数的影响[6]。因此，本文将粒子群算法分别与2个单目标函数和1个多目标函数组合，用于率定SWMM模型参数，并构建了1个理想模型和1个实际模型以比较分析不同目标函数对参数率定结果的影响，以期为SWMM模型参数率定提供可行的方法。

2 数据来源与研究方法

2.1 研究区概况

焦东片区位于国家海绵城市建设试点城市——镇江市主城区东北部，面积为6.51km2。片区内水系较为发达，主要河道分为两“横”四“纵”，两“横”由南至北分别为一夜河和二夜河，四“纵”分别为友谊港、胜利港、大寨港河前进港(如图1所示)。片区部分管网设计标准偏低，排水能力小于1年一遇的管道占比48.07%[7]。焦东片区多年平均降雨量1063.1mm，雨季主要集中在7、8、9三个月，频发的暴雨导致主城区内涝积水严重，给居民生产生活带来很大不便。

2.2 数据概况

本文收集了研究区2019—2021年5min间隔的降雨和流量数据，数据监测点见图1。基于收集到的数据，依据皋云等[8]确定的适用于镇江的降雨场次划分方式，划分了40场包括不同雨型、雨强和历时的降雨事件。为构建SWMM模型，从镇江市住建局和镇江市京口区水利局获得了分辨率为5m的DEM数据、土地利用数据、管网、河道等数据。

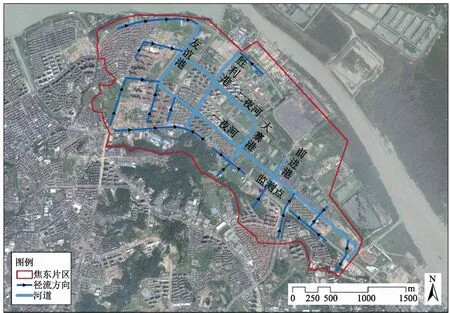
图1 焦东流域水系及径流方向图

2.3 率定方法

2.3.1粒子群算法

粒子群算法由Kennedy和Eberhart于1995年提出的一种进化计算技术[9]，源于对鸟群捕食的行为研究。在粒子群算法中，每一个优化问题的解都是搜索空间中的一个微粒，所有的微粒都有一个被优化的函数决定的适应值，每个微粒还有一个速度决定它们移动的方向和距离，然后微粒群就追随着当前最优微粒在解空间中搜索。粒子群算法的核心公式见公式(1)和(2)，伪代码见表1，详细的计算原理可参考文献[10- 11]。

(1)

(2)

2.3.2率定目标函数

考虑到城市防洪减灾重点关注洪涝过程中的流量峰值和总流量，本文建立了2个单目标函数，即最小化流量峰值模拟误差(F1(x))，最小化总流量误差(F2(x))，和一个多目标函数，即同时最小化流量峰值误差和总流量误差，用于率定SWMM参数。公式为:

(3)

(4)

式中，Qobs(i)—观测的流量峰值，m3/s；Vobs(i)—观测的总流量，m3；Qsim(i)—模拟的流量峰值，m3/s；Vsim(i)—模拟的总流量，m3；n—用于率定SWMM参数的降雨场次数。

2.4 模型构建

为了验证粒子群算法能否在理论上找到SWMM参数最优解，本文先构建了一个理想模型以避免模型输入(即降雨观测误差)、模型结构不确定性等方面带来的误差。在理想模型结果的基础上，再利用一个真实的流域案例来检验粒子群算法应用于实际情况的效果。

2.4.1理想模型

如图2所示，理想模型共有7个子汇水区，8个节点(包括一个出口节点)，和7条管道(其中2条代表河道)。在SWMM模型中使用Horton法模拟下渗过程，使用动力波方法演算汇流过程。基于已有的关于SMMM参数敏感性的研究成果[12- 14]，选取了7个主要参数作为率定目标(见表2)。表2给出了参数的“真实值”及推荐的取值范围，理想模型使用“真实值”和观测的降雨事件作为模型输入以得到出口节点的“观测”径流过程。在理想模型中，粒子群算法分别与2.3.2节中的不同目标函数组合以率定理想模型的参数，每种组合重复运行50次以避免随机性。

图2 理想模型示意图

表2 需率定的参数及其意义、“真实值”和取值范围

2.4.2实际模型

基于焦东片区构建了实际模型，如图3所示，实际模型包括295个子汇水区，201条管道，90条河道，和290个节点(包括2个出口节点)。与理想模型相同，下渗过程采用Horton法，汇流演算采用动力波。观测到的40场降雨事件被作为SWMM模型的输入，在监测点获得的相应流量数据作为率定目标。在这些事件中，前35场事件被用于模型率定，后5场事件被用于模型验证。根据不同目标函数在理想模型中的表现，选择最合适的目标函数应用于实际模型的参数率定。

图3 焦东片区概化示意图

2.5 精度评价

SWMM模型的模拟精度由以下指标评价：

(1)纳什系数：

(5)

(2)流量峰值相对误差：

(6)

式中，Pobs—观测的流量峰值，m3/s，Psim—模拟的流量峰值，m3/s。

(3)总流量相对误差：

(7)

式中，Vobs—观测的总流量，m3，Vsim—模拟的总流量，m3。

(4)峰现时间误差：

(8)

3 结果与分析

3.1 理想模型

表3给出了经粒子群算法与不同目标函数率定后的SWMM模型表现的评价指标。接近于1的CORR和NSE值表明不同目标函数率定的SWMM模型的模拟径流过程与实际径流过程基本吻合。然而在总流量和流量峰值方面，不同目标函数率定的SWMM模型表现出差异性。以流量峰值为目标率定的SWMM模型模拟的REp和EPt较小，而REv较大。与之相反，以总流量为目标率定的SWMM模型模拟的REv较小，而REp和EPt较大。这一结果表明基于单目标函数的参数率定容易只侧重于总流量与流量峰值中的一个方面而忽略了另一个方面。与单目标函数的率定结果相比，多目标函数率定的SWMM模型的REv、REp和EPt均较小，兼顾了峰值和总流量的模拟精度。图4给出了不同目标函数的50次率定后的参数分布范围(参数经过归一化处理)。如图4所示，虽然不同目标函数都无法找到部分参数的“真实值”，但多目标函数率定得到的参数更接近“真实值”，散布范围更小。

表3 不同目标函数率定的SWMM模型径流模拟结果

因此多目标函数更适用于SWMM模型的参数率定。后续可在采用多目标函数的基础上，改进粒子群算法以进一步提高参数率定精度。

3.2 实际模型

理想模型的结果表明粒子群算法与多目标函数率定得到的SWMM模型模拟结果优于单目标函数率定的结果，因此实际模型采用多目标函数。从35场率定降雨事件和5场验证降雨事件中分别选取2场降雨事件作为代表，率定结果见表4，模拟的径流过程线如图5—8所示。多目标率定的SWMM模型在4场暴雨条件下的模拟效果均较好，率定结果可以接受。与理想模型相比，实际模型率定结果误差更大，这可能是源于降雨-径流观测误差，模型概化误差等方面。

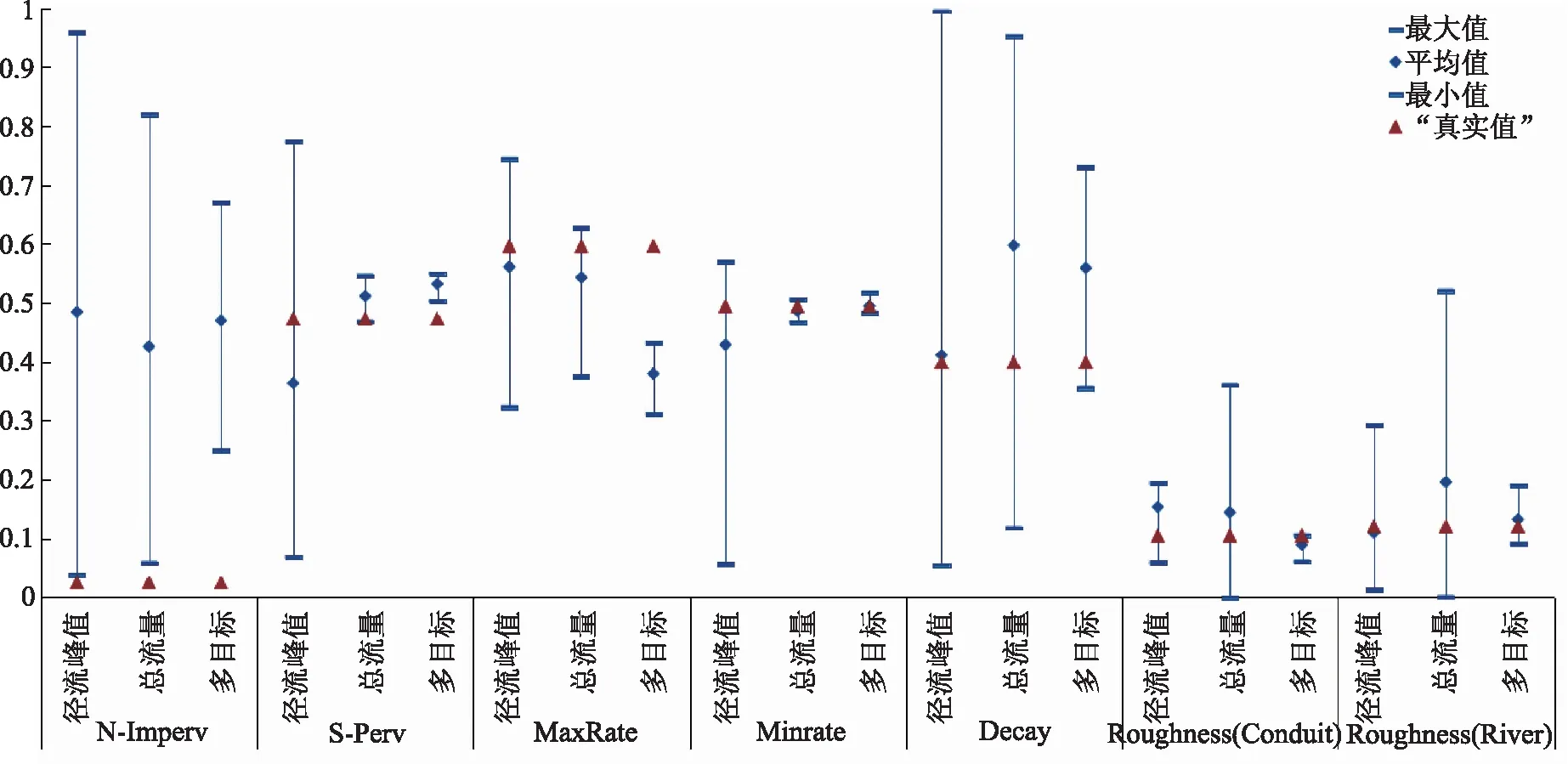
图4 不同目标函数率定得到的参数分布范围

表4 多目标函数率定的实际模型的模拟结果

图5 20190706#场次降雨径流模拟过程线

图6 20190810#场次降雨径流模拟过程线

图7 20200717#场次降雨径流模拟过程线

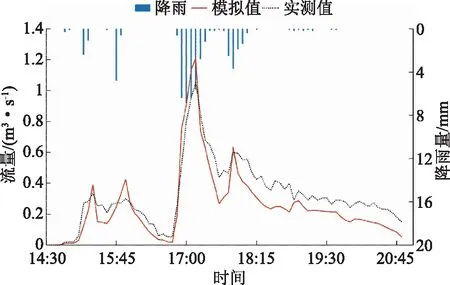
图8 20200826#场次降雨径流模拟过程线

4 结论

本文利用1个理想模型与1个实际模型比较了粒子群算法与不同目标函数的组合率定SWMM模型参数的效果。在理想模型中，多目标函数的率定结果优于单目标函数，可同时保证总流量和流量峰值的模拟精度。在实际模型中，多目标函数率定的SWMM模型仍能得到可接受的模拟精度。与单目标函数相比，粒子群算法与多目标函数的组合更适合SWMM模型的参数率定。后续可在采用多目标函数的基础上，进一步改进粒子群算法以提高参数率定精度。