探析内在逻辑 把握数学本质*——2022 年高考文科数学全国甲卷第19 题解法剖析与思考

云南师范大学数学学院;云南师范大学教育学部(650500) 华子艳

昆明市官渡区钟英中学(650200) 黄赛春

云南师范大学数学学院(650500) 刘冰楠

《普通高中数学课程标准(2017 年版2020 年修订)》(以下简称《标准》)提出: 立体几何研究现实世界中物体的形状、大小与位置关系[1]的要求.2022 年高考文科数学全国甲卷第19 题(以下简称“2022 年文科甲卷第19 题”)以封闭包装盒设计呈现试题,相较于历年立体几何题,增加了现实情境的创设,体现理论联系实际,落实新课程改革中综合实践活动在试题中的应用.此题解法多变,偏重基础知识的灵活运用,注重通性通法和空间思维能力的考查,彰显素质教育“四翼”的要求以及高考命题稳中求新的特点,利于学生思维品质和关键能力的培养.

1 试题再现

题目(2022 年文科甲卷第19题) 小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图1 所示: 底面ABCD是边长为8(单位: cm)的正方形,∆EAB,∆FBC,∆GCD,∆HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.

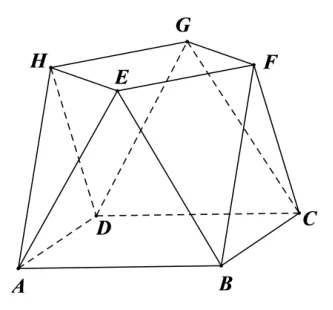
图1

(1)证明:EF//平面ABCD;

(2)求该包装盒的容积(不计包装盒材料的厚度),

2 解法探析

高考是国家选拔人才的重要途径,是实现立德树人的重要载体和素质教育的关键环节[2].相较于历年立体几何试题,2022 年文科甲卷第19 题在情境创设与图形直观呈现上有所创新,本质上考查的仍是线面位置关系、图形体积等数学核心主干知识,在解题过程中需对基础知识进行综合运用、融会贯通,利于数学抽象、逻辑推理、数学运算等核心素养的培养,体现高考命题对素质教育目标的考查.

第(1)问证明线面平行,属常规问题.基本思路是将线面平行转化为面面平行或线线平行.方法有平行四边形法、投影法、补形法、向量法等,利于提升学生空间思维感及解法综合应用能力.第(2)问求多面体的体积,需对分割与补形法灵活应用,对抽象能力有较高要求,能帮助学生建立整体与局部的联系,树立空间模型观念.

2.1 第(1)问解法探析

证法1(平行四边形法)因为∆EAB,∆FBC均为正三角形,且底面ABCD为正方形,易得两个三角形全等.如图2 所示,分别取AB,BC中点记为E1,F1,连接EE1,E1F1,FF1,得EE1⊥AB,FF1⊥BC,EE1=FF1.因为三角形所在的平面都与底面ABCD垂直,且平面EAB,平面FBC与底面ABCD的交线分别为AB,BC,故EE1//=FF1,所以四边形EE1F1F为平行四边形,即得EF//=E1F1.又因为平面ABCD,E1F1⊂平面ABCD,所以EF//平面ABCD.

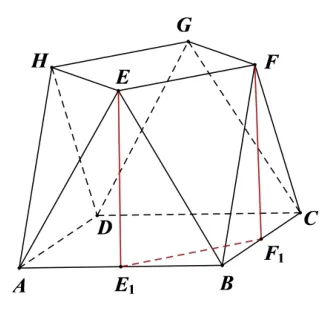
图2

证法2(投影法)由题意得∆EAB,∆FBC均为正三角形,且∆EAB,∆FBC均垂直于底面正方形ABCD.如图3所示,分别取AB,BC中点为E1,F1,连接EE1,E1F1,FF1,得EE1⊥正方形ABCD,FF1⊥正方形ABCD,即得E1F1为EF的投影.且E1,F1分别为AB,BC的中点.连接AC(如图3),因为四边形ABCD为正方形,所以E1F1//AC,即得EF//AC.又因为平面ABCD,AC ⊂平面ABCD,所以EF//平面ABCD.

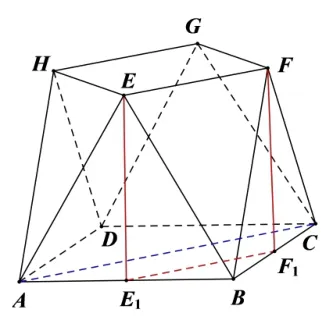
图3

证法3(面面平行法) 分别取AB,BC,CD,DA的中点为E1,F1,G1,H1,连接EG,HF,E1G1,H1F1(如图4),再连接HH1,EE1,GG1,FF1(如图5).根据解法1 可得EG//E1G1,HF//H1F1,因为EG,HF是平面EFGH内两条相交直线,E1G1,H1F1是平面ABCD内两条相交直线,故平面EFGH//平面ABCD,又因为EF ⊂平面EFGH,所以EF//平面ABCD.

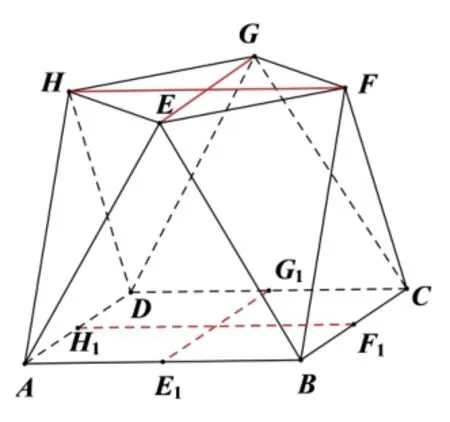
图4

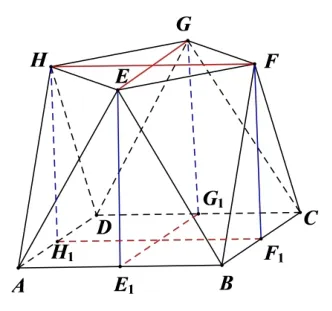
图5

证法4-1(补形法的综合运用)如图6 所示,过A,B,C,D分别作平面ABCD的垂线为A1A,B1B,C1C,D1D,再分别过E,F,G,H作AB,BC,CD,DA的平行线,交点为A1,B1,C1,D1,连接交点形成几何体ABCD −A1B1C1D1,依题意可知几何体ABCD −A1B1C1D1为长方体,且E,F,G,H分别为A1B1,B1C1,C1D1,A1D1的中点.连接A1C1,AC(如图7),由长方体的性质可得EF//A1C1,A1C1//AC.由平行的传递性得EF//AC.又因为平面ABCD,AC ⊂平面ABCD,所以EF//平面ABCD.

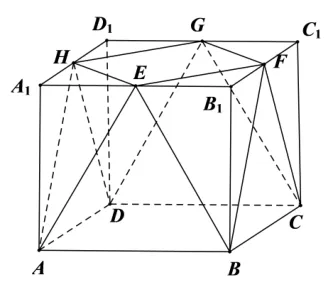
图6

图7

证法4-2(补形法的综合运用)通过补形,可得在长方体ABCD −A1B1C1D1中,EF所在的平面EFGH与平面ABCD平行,即得平面EFGH//平面ABCD,因为EF ⊂平面EFGH,所以EF//平面ABCD.

在当今世界政坛群星之中，拉加德绝对是极其独特的存在：她是国际货币基金组织历史上的第一位女总裁，上任前却饱受争议，但凭借多种因素成功连任；她曾被讥讽为“失言部长”，后来却成为法国近代以来任职时间最长的财政部长；她是地道的法国人，学业却在美国完成，更曾在美国工作了几十年，思维方式严重“美国化”。

证法5(向量法)如图8 所示,分别取AB,CD中点为O,G1.以O为原点,OB为x轴,OG1为y轴,OE为z轴建系.

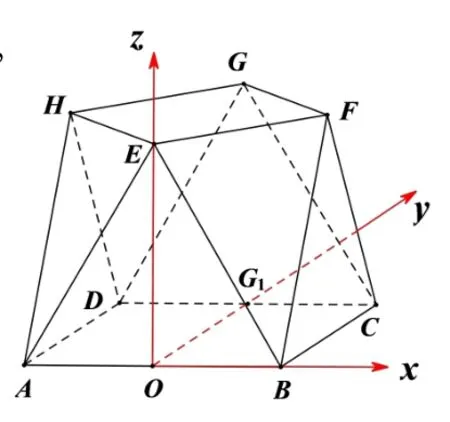
图8

依题意可得OB⊥OG1⊥OE,OE==(4,4,0),因为平面ABCD在坐标平面xoy内,故设平面ABCD的法向量n=(0,0,1),所以·n=0,所以EF//平面ABCD.

其他建系方法大同小异,不再赘叙.

评析以上解题思路呈现如图9 所示.线线平行、线面平行、面面平行是立体几何的三种基本位置关系,可相互推导.第(1)问需证线面平行,基本思路是将线面平行转化为面面平行或线线平行.多数学生最先能想到的是平行四边形法(解法1),该法为高中立体几何最常用的“通法”之一.其内在逻辑是寻找线线平行,证明线面平行,难点在于选择恰当位置进行平行四边形构造.投影法(解法2)也可辅助寻找线线平行,将直线投影至所证平面,转化空间问题为平面问题,有效降低解题难度,渗透降维思想.当线线平行证明出现困难时,可转换思路至寻找面面平行,利用面面平行(解法3)的性质构造相交辅助线简洁进行证明.以上三种解法注重空间想象能力与逻辑思维能力的考查,利于学生数学抽象、逻辑推理等核心素养的培养.

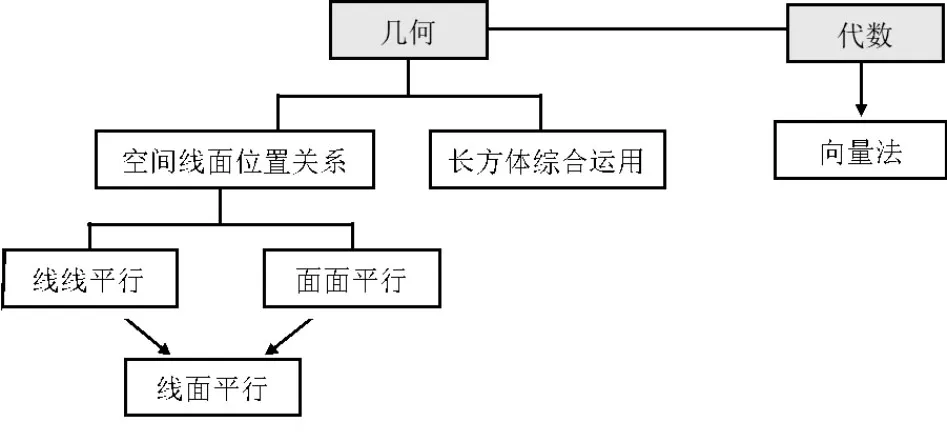
图9

鉴于本题几何体形状较为特殊,学生在选择解法1、2、3时,会受制于自身的空间感与想象力.《标准》提出: 借助长方体,直观认识空间点、直线、平面的位置关系[1]的指导.因此可将复杂图形补形为规则的长方体(解法4),利用长方体自身性质辅助证明,将复杂空间位置关系简单化,有助于提高学生图形思维意识,感悟转化与化归思想.

以上方法均属几何解法,事实上,将几何问题化为代数求解也是学生在解题中常用的方法,如向量法(解法5)通过建立直角坐标系,以代数形式表示线与面的关系,既降低空间想象难度,又有效考查逻辑思维与运算求解能力,利于渗透数形结合思想.

2.2 第(2)问解法探析

解法1 (补形: 长方体)同第一问解法4,如图6 所示,作辅助线得长方体ABCD −A1B1C1D1.由第(1)问解法5 得该长方体的高为AA1=,故

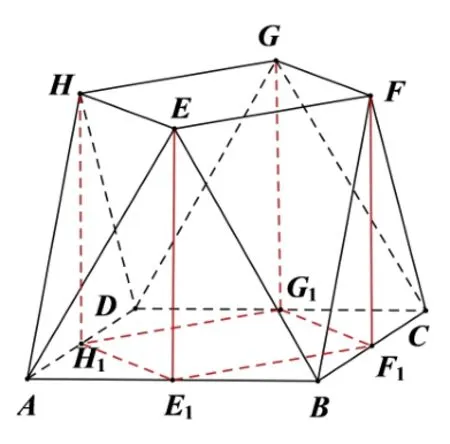
图10

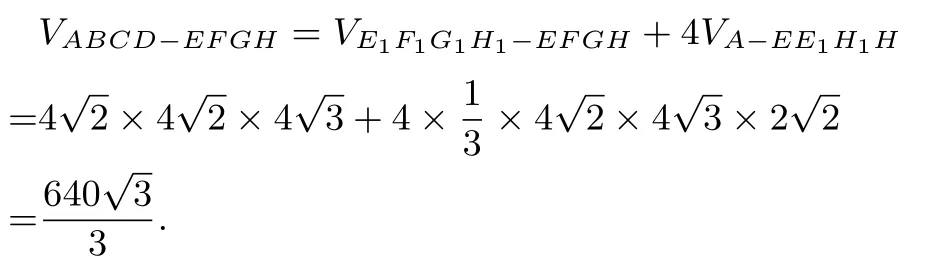
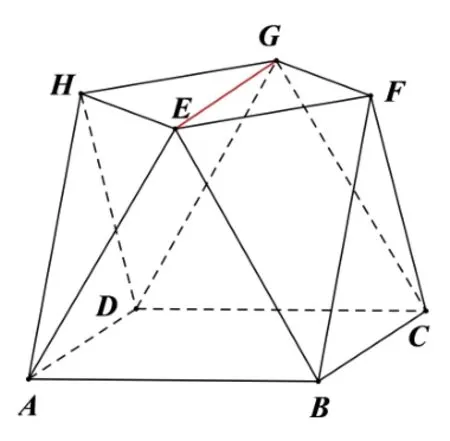
图11

解法4(分割: 三棱锥+四棱锥)如图12 所示,连接AC,BD交于点O,再连接OE,OF,OG,OH.则该几何体的体积由四棱锥O −EFGH的体积和4 倍三棱锥A −OEH的体积以及4 倍三棱锥E −OAB的体积组成.依题意易得OE=OF=OG=OH=8,取EH的中点P,AB的中点E1,连接AP,OP,EE1,则EH垂直平面APO.由图可知,三角形APO,四棱锥O −EFGH与三棱锥E −OAB的高均为EE1的长.故

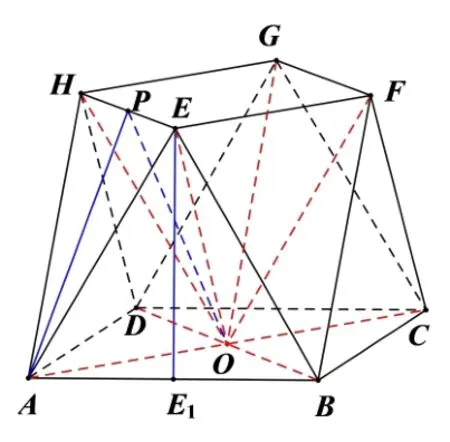
图12

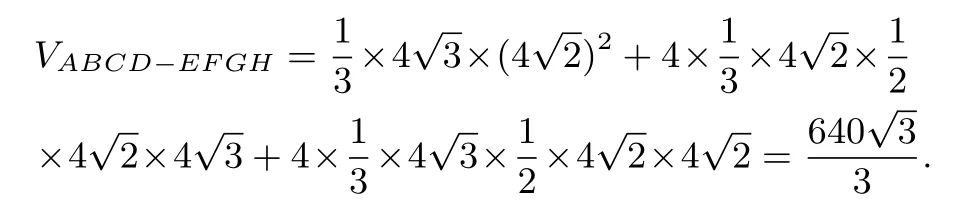
评析以上解法为我们提供立体几何的研究与求解思路: 可从空间几何体的整体观察入手,抽象出组成空间图形的基本元素——点、线、面,并结合长方体直观认识这些组成元素的位置关系[3].综观分割法与补形法,提炼出内在逻辑.即把不熟悉的几何体转化为熟悉的基本几何体,如长方体、三棱锥、三棱柱、四棱锥等,学生需要洞察隐藏在图形中与解决问题相关的子图形,按求解需求添加辅助线[4].因此分割与补形法的使用能加强学生有机联系整体和局部的意识,聚焦数学抽象、直观想象、逻辑推理等核心素养的培养,渗透数形结合、转化与化归等数学思想.

3 错因分析与变式训练

3.1 错因分析针对学生错因进行分析,有助于深化对问题本质的理解,发现解决问题的新视角与新思路.基于广泛调研,可将学生的错因归结为以下两点: 能力性失误与心态性失误.其中,第一类失误主要缘于学生对基础知识和基本技能掌握的不扎实,导致知识迁移能力较弱,无法灵活运用题干中的关键性条件.如无法由题干推知长方体补形条件、空间位置关系的转化不合理等.第二类失误偶然性较大,考场中受到环境以及心理等因素制约,学生易出现遗漏条件、计算失误、逻辑混乱等问题致使失分,如试题第(2)问体积计算中,存在考生辅助线绘制模糊,导致数据运算出错等.

3.2 变式训练在对题目进行错因分析后,设计试题变式,利于教师对学生易错点进行正确归因,进而明晰教学要点,提高教学质量.同时,通过多组变式训练,学生也能体会条件与问题间的联系,深刻把握知识的内在逻辑,加深对数学知识的本质理解.有助于学生分析问题和解决问题能力的提升,增强思维的灵活性、拓展性和发散性.因此,可在试题情境不变的情况下,对题目进行如下变式:

小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图1 所示:

变式1(针对思维灵活性)底面ABCD是边长为8(单位: cm)的正方形,∆EAB,∆FBC,∆GCD,∆HDA所在的平面都与平面ABCD垂直,且EF=GF=GH=HE.求直线EF与平面ABCD所成角的余弦值.

变式2(针对思维拓展性)底面ABCD是边长为8(单位: cm)的正方形,∆EAB,∆FBC,∆GCD,∆HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.求平面ABE、平面EFGH与平面EFB夹角的余弦值.

变式3(针对思维发散性)底面ABCD是边长为8(单位: cm)的正方形,∆EAB,∆FBC,∆GCD,∆HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.请利用至少四种以上的方法证明:EF//平面ABCD.

变式探析变式过程须把握不同内容间的核心关联,做到“万变不离其宗”,“宗”即指顺应并适合每个学生达到数学学习的目标[5].变式1 同时改变了题目条件与提问方式,但结果仍与原试题相同,能训练学生把握试题中“变”与“不变”的本质,考查学生思维的灵活性;变式2 将问题改编为求二面角余弦值,此类求解多出现于理科试题中,有助于增加立体几何知识考查的深度和广度,提升思维的拓展性;变式3将“一题多解”直接融入提问,在解题过程中精准而直接地发散学生思维,实现知识的融会贯通.三种变式分别针对学生思维的不同角度进行设计,层层递进,可有效对不同学生进行不同方向的提升,体现变式题中的差异化,也为教师课堂多样性提供途径.

4 教学建议

通过对2022 年文科甲卷第19 题的思路探索,探究其思想方法和转化策略,管窥高考命题的考查方向与核心功能,以期发挥高考的选拔与引导功能,为教师教学提供参考与借鉴.

4.1 探析内在逻辑,锤炼数学思维.立体几何题虽千变万化,总蕴含其内在逻辑.通过解法探析,能明确基础知识间存在的逻辑联系,如本题第(1)问中线线、线面、面面平行的转化与推导,由几何到代数、整体到局部的思路追溯,完成知识网络与解题框架的构建.因此在解题训练时,可引导学生多角度思考,拓宽解题思路,有效内化知识并将其灵活运用.教师在教学中巧用一题多解与变式训练,也能有效破除学生思维定势,锤炼其思维的灵活性与开放性,培养学生综合分析问题、解决问题的能力.

4.2 把握数学本质,增强教学成效.理解数学把握本质就是要深刻剖析概念内涵,准确理解数学思想[6].立体几何题型灵活多变,教师采用套路式教学会导致学生在考场上“动一发而溃全军”.因此解题训练需注重数学本质与通性通法,提升学生核心素养与关键能力.近年来高考命题趋于基础性、综合性与创新性,在教学实践过程中,教师可精选试题内容,而后进行深度剖析,再加以变式训练,学生由此能举一反三、触类旁通,充分发挥试题训练“减负增效”的功能之助.

4.3 理论联系实际,发挥育人价值.当前教育面临的最大困境恰是学校教育和现实世界的隔离,学生既不能充分运用生活中既有的经验,也不能将学校所学迁移到未来的问题解决中去[7].2022 年文科数学甲卷在立体几何21 题中创设现实问题情境,将数学真正用到实处,也使学生真正学到实处,落实立德树人根本任务,凸显命题的应用性.试题几何图形新颖,解题路径多样,利于渗透数学思想方法,提升核心素养考查的有效性.因此,教师在立体几何教学中可将现实情境引入,不但能激发学生学习兴趣,也能有效考查学生分析和解决问题的能力,增强其空间思维能力,培养学生在数学中观察、思考、表达现实世界的学习习惯.