定弦定角在解题中的运用

王 黎，马绍文

(云南师范大学数学学院，云南昆明，650500)

定弦定角问题：动点对某条长度恒定的线段张成的角固定不变，即动角的大小恒定不变，该线段称为“定弦”，定弦所对的角称为“定角”.

预备知识：

知识点1如图1，以AB为直径的⊙O上有一动点，则∠ACB恒为90°；反之当∠ACB=90°时，点C一定在以AB为直径的圆上.

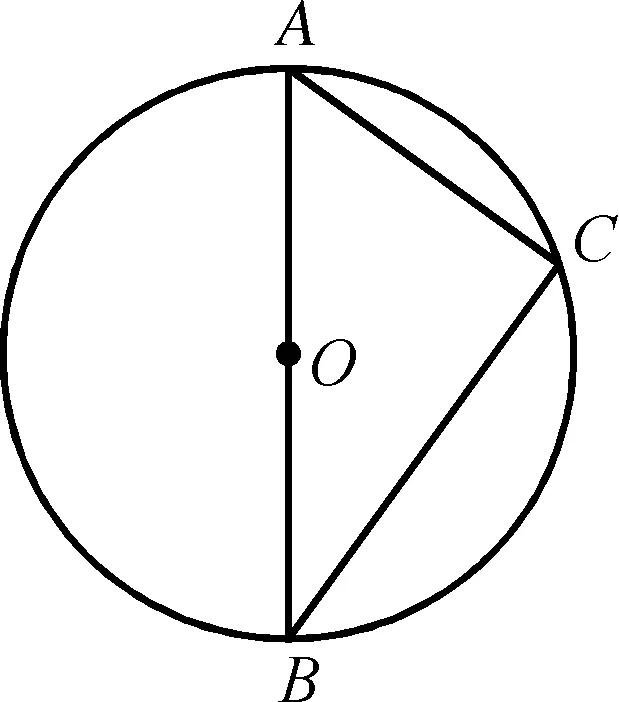
图1

知识点2如图2，在⊙O中，弦AB一定时，则该弦所对应的劣弧(或优弧)上的圆周角∠ACB就一定；反之当∠ACB为一定值时，点C一定在以AB为弦的圆上.

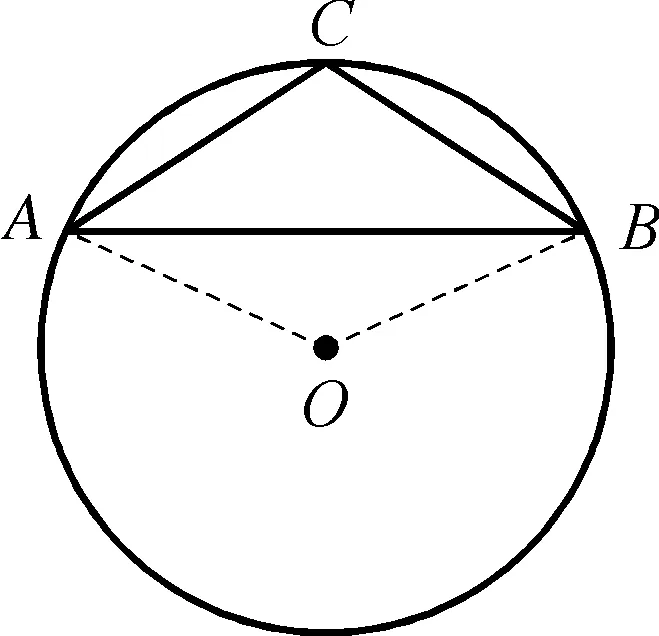
图2

1 求最值问题

例1(2021广东中考)在△ABC中，∠ABC=90°，AB=2，BC=3，点D为平面上的一个动点，∠ADB=45°，则线段CD的最小值为( )

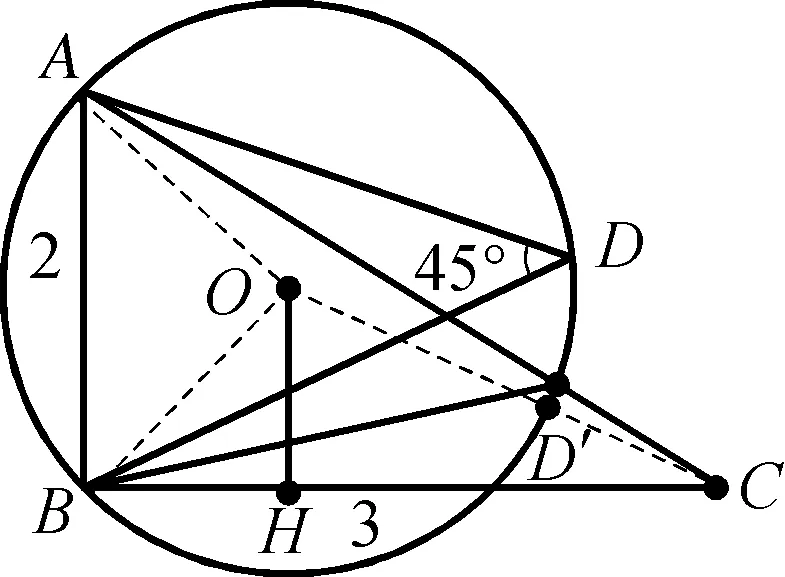
图1-2

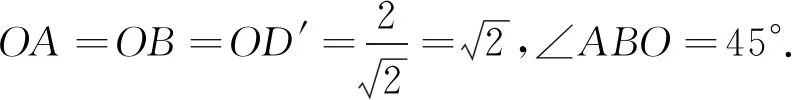
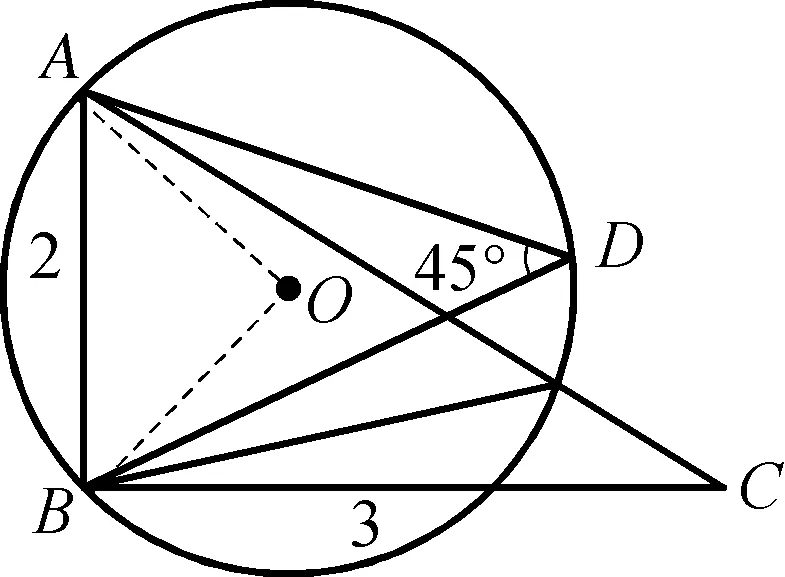
图1-1

例2如图2-1，已知正方形ABCD以BC为腰向正方形内部作等腰△BCE，其中BE=BC，过点E作EF⊥BC，点P是Rt△BEF的内心，连接AP，若正方形的边长为2，求AP的最小值.

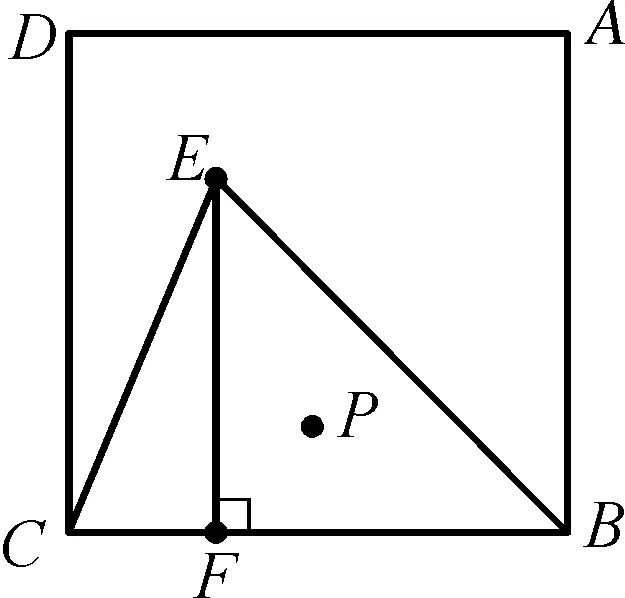
图2-1

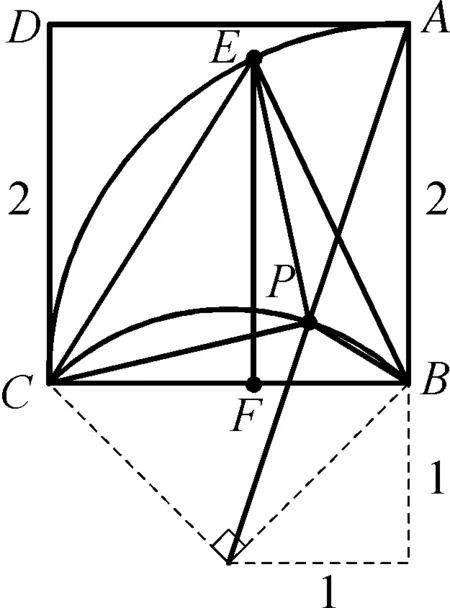
图2-3

点E是动点，Rt△BEF也随之改变，则内心P也随之改变，CB所对应的圆周角为135°，因此所对应圆心角为90°，作CB的垂线可以找到圆心，即可找到点P的运动轨迹.

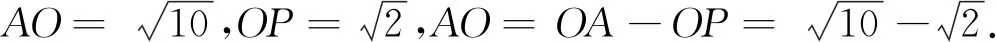
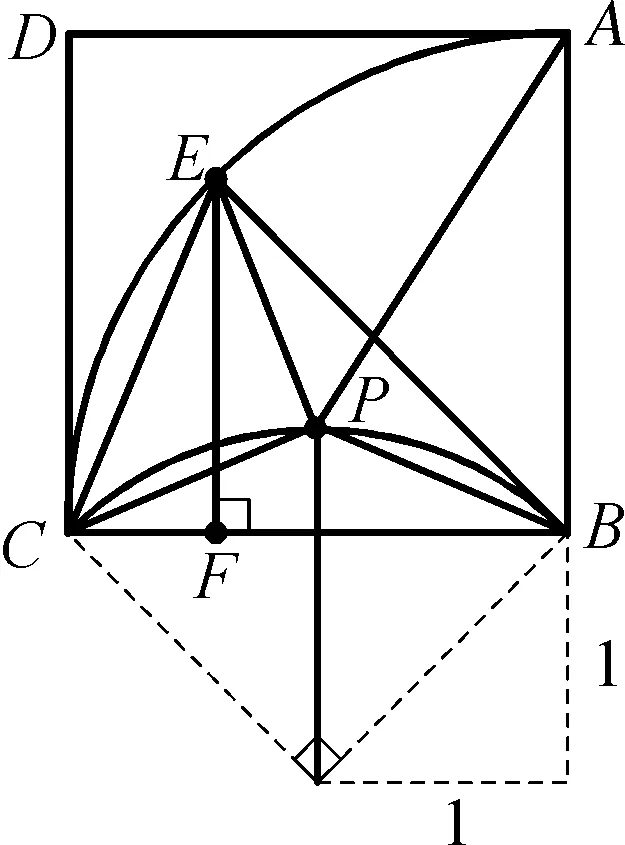
图2-2

2 路径长问题

例3如图3-1，在菱形ABCD中，∠ABC=60°，AB=4，E是AB边上的动点，过点B作直线CE的垂线，垂足为F，当点E从点A运动到点B时，点F的运动路径长为( ).

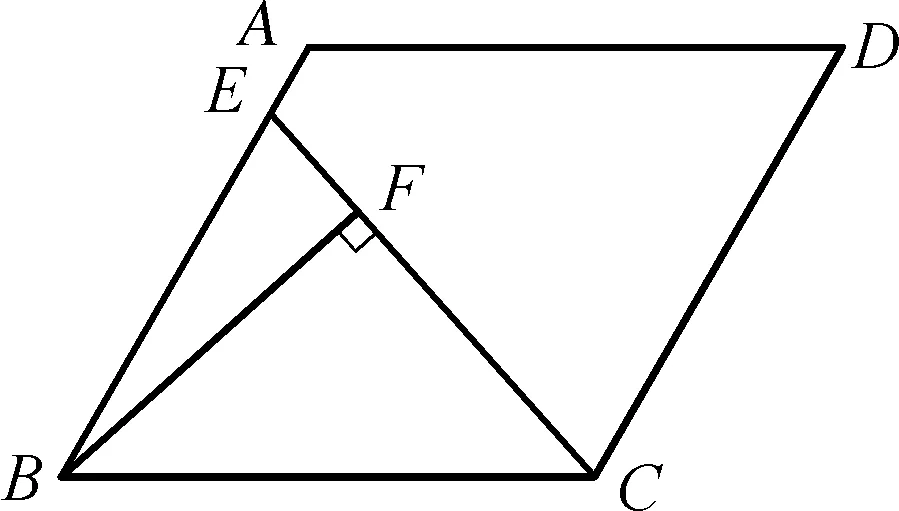
图3-1

解析：由题目可知，在点E的运动过程中，∠BFC=90°始终成立，即定弦BC的对角是定角，构成定弦定角模型.因此点F的运动轨迹是以BC为直径的圆弧.需要确定点F的起始位置和终点位置.如图3-2，起始位置是点A，E重合，此时点F是菱形ABCD对角线的交点O，终点位置是点B，E重合，此时点F是点B.所以点F的运动轨迹是以BC为直径的圆上的劣弧BO.

图3-2

∠CGO=∠ABC=60°.

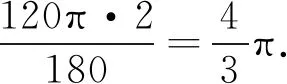
例4如图4-1，在等腰Rt△ABC中，AC=BC=2，点P在以斜边AB为直径的半圆上，M为PC中点，当P点沿半圆从点A运动到点B时，点M运动的路径长是( )

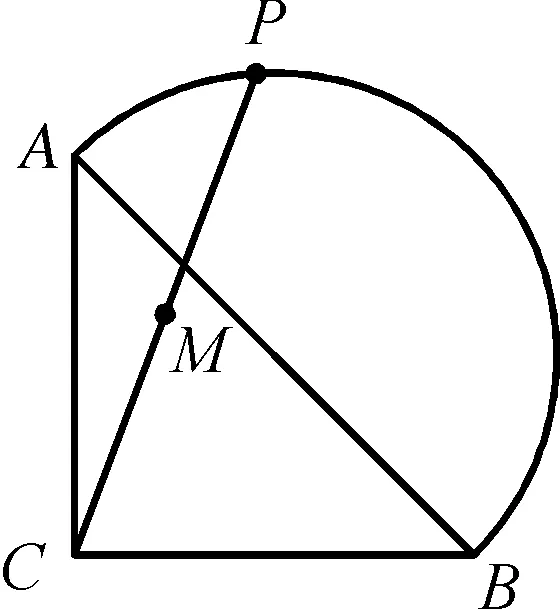
图4-1

解析：如图4-2所示，设O是AB的中点，分析可得OM垂直平分于弦PC，所以∠CMO=90°.

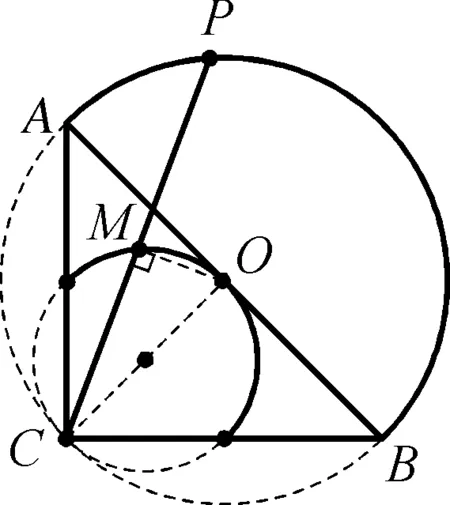
图4-2

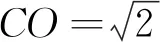
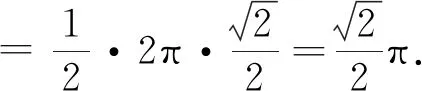
3 定弦定角求面积最值

例5如图5-1，已知四边形ABCD满足BC=CD，∠BCD=60°，∠BAD=90°，AC=6，则四边形ABCD面积的最小值是( )

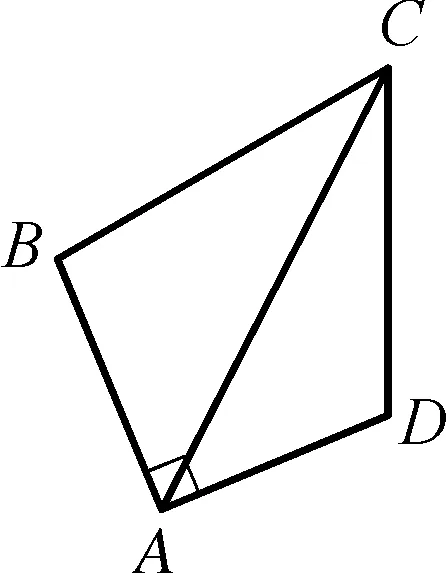
图5-1

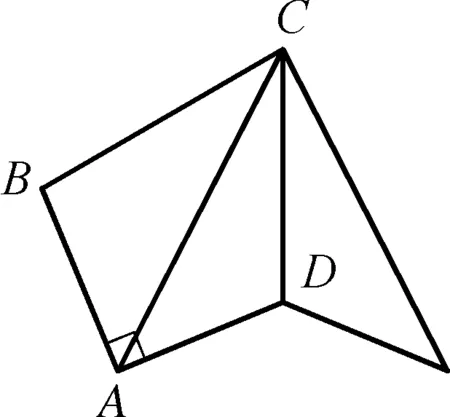
图5-2

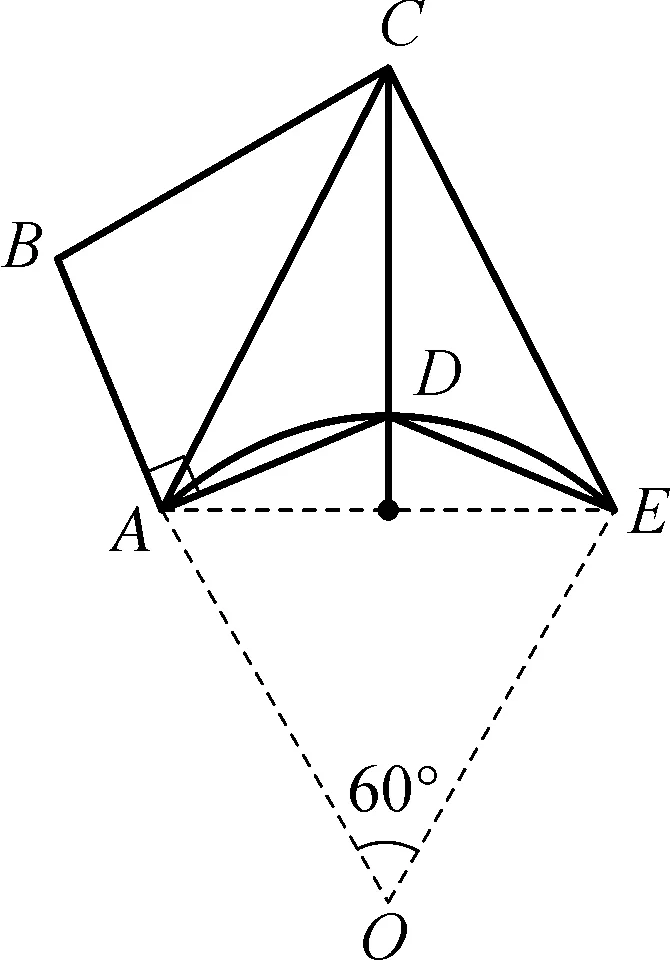
图5-3

解析：三点共线问题，首先把△CBA绕点C逆时针旋转，此时△CBA≅△CDE，求四边形ABCD面积最小转化为求四边形CADE面积最小.

∵△CBA≅△CDE⟹CA=CE，∠BCA=∠DCE，∠CAB=∠CED.

∴∠ACE=60°⟹△CAE是边长为6的等边三角形.

SACDE=SCAE-SADE，SCAE是已知的，当四边形CADE面积最小时即SADE最大.

∠ADE=∠ACD+∠DCE+∠CAD+∠CED=90°+60°=150°.

∠ADE是固定的，AE的长也是固定的，可转化为一个定弦定角问题.

弦AE对应圆周角是150°，所以对应圆心角是60°.

点D的运动轨迹是一段以O为圆心以AO(OE)为半径的圆弧.

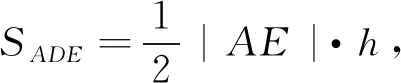
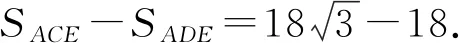
4 “手拉手”模型与定弦定角

“手拉手”定义：两个顶角相等且共顶点的等腰三角形形成的图形.因为共顶点相连的四条边，可以形象地看作两双手，左手拉左手，右手拉右手，所以被称为“手拉手”模型.

“手拉手”全等(图6-1)：AB=AC，AD=AE，且∠BAC=∠DAE.

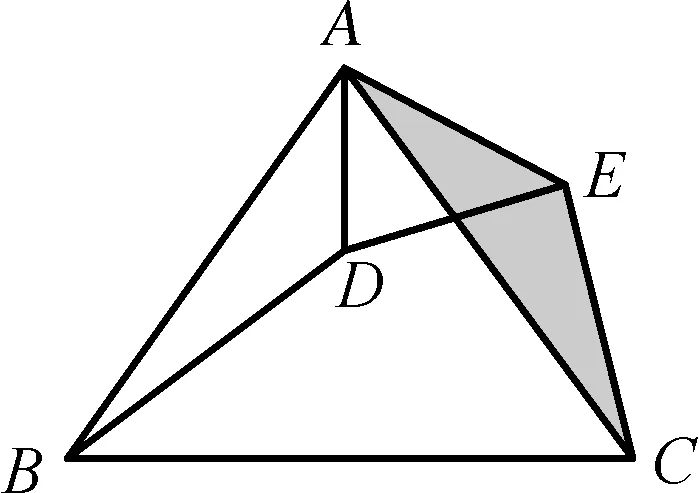
图6-1

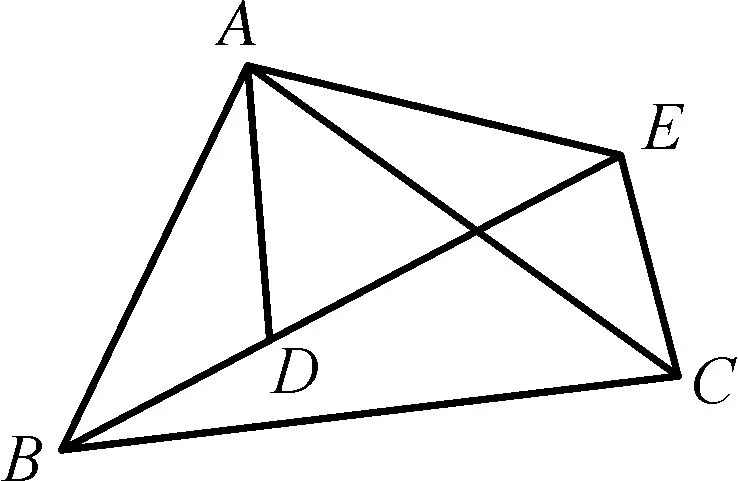
图6-2

例6如图6-3，在Rt△ABC，∠ACB=90°，AB=4，AC为边作正△ACD，连接BD，求BD的最大值.

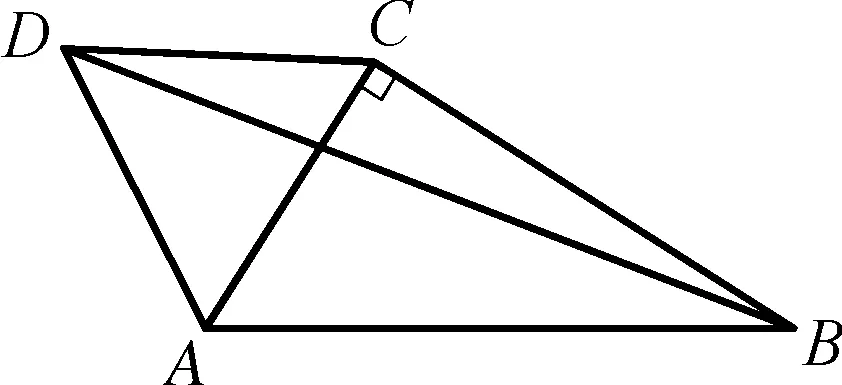
图6-3

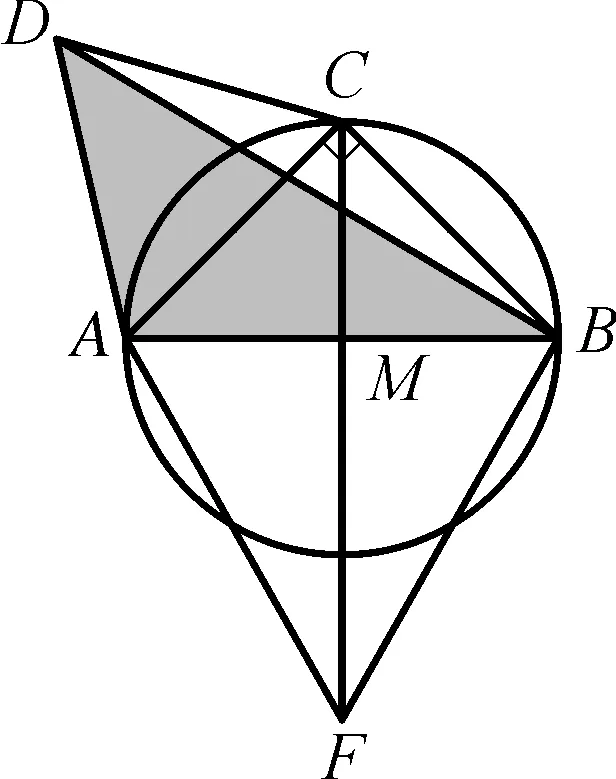
图6-4

解析：由∠ACB=90°，AB=4可知(弦AB的对角是定角，构成一个定弦定角)，点C在以AB为直径的圆上，弦AB是不变的就以AB为边作正△ABF，易得∠DAB=∠CAF，构成一个手拉手模型.

容易证明出：△DAB≅△CAF，∴BD=CF.

当CF过圆心M时最大.

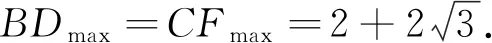
5 求边长数量关系问题

例7(2018广州中考)如图7-1，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC.连接BD，探究AD，BD，CD之间的数量关系.

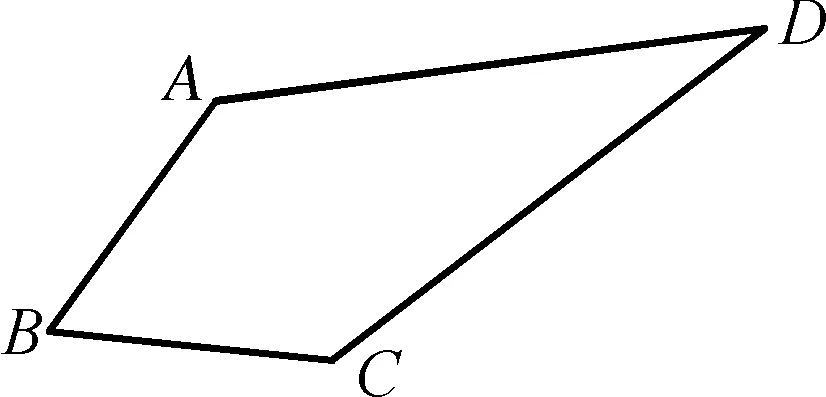
图7-1

解析：连接AC，由∠B=60°，AB=BC，易得出△ABC为等边三角形.由∠D=30°，AC是确定的，可以得到这是一个定弦定角问题.作点B关于线段AC的对称点B′，然后再以点B′为圆心，AB′为半径作圆弧，则点D可以是圆弧上的任意一点.

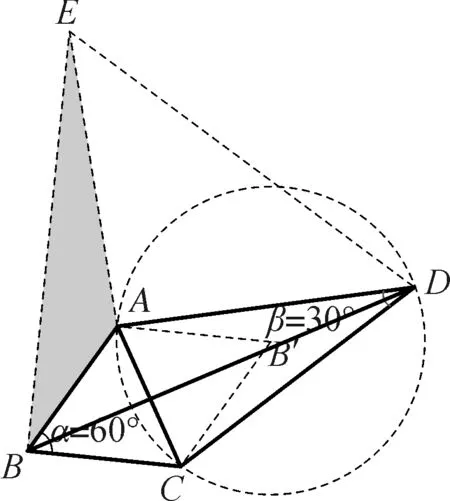
图7-2

如何探究这三条线段之间的数量关系，我们发现这三条线段是分散的，可以通过旋转作全等变换，把分散的线段集中起来.

将△BCD绕点B逆时针旋转60°得到△BAE，所以△BCD≅△BAE.

得出CD=AE，BD=BE，∠BCD=∠EAB.

∵BD=BE，∠EBD=60°.

∴△EBD是等边三角形.∴BD=ED.

∵∠EAD=360°-(∠EAB+∠BAD)

=360°-(∠BCD+∠BAD)=360°-270°=90°.

∴EA2+AD2=ED2.∴AD2+CD2=BD2.

总之，定弦定角问题都有一个固定的解题方法，其解题思路其实是一样的，需要学生在认真分析问题的基础上，通过定弦定角找到“隐圆”.也可进行反向思考，要想得出答案，就必须具备什么样的条件，在猜测的基础上一步步找出题目给出的隐含条件，帮助解决问题.希望以上定弦定角的应用方法和策略能够为初中数学教师和学生起到良好的理论指导作用，帮助学生更快速、更便捷地解决这部分的问题.