面向全局和工程优化问题的混合进化JAYA算法

刘景森，杨 杰，李 煜

1) 河南大学智能网络系统研究所，开封 475004 2) 河南大学软件学院，开封 475004 3) 河南大学管理科学与工程研究所，开封 475004

优化问题普遍存在于生产生活的诸多领域，近年来，全局优化问题越来越复杂，规模越来越庞大，具有高维、非线性、目标函数不可导等特点，传统的优化方法已经很难有效地进行求解，而基于群体搜索的元启发式智能优化算法却获得了较好效果，引起学者们的广泛青睐和研究.如：受鸟群捕食过程启发提出的粒子群算法[1–2]，受正余弦函数数学模型启发而提出的正弦余弦算法[3–4]，受座头鲸捕食行为启发提出的鲸鱼优化算法[5]，受量子力学原理和基于量子的原子模型启发提出的原子轨道搜索算法[6]等.这些智能优化算法的不断提出、改善和优胜劣汰，为求解大规模复杂全局优化问题提供了新思路.

函数极值优化问题是测试算法寻优性能的主要方法，而工程设计约束优化问题则是智能优化算法的重要应用领域.工程设计问题广泛存在又难以求解，其目标函数与约束条件的非线性以及决策变量搜索空间不可行域的出现，使得传统优化方法束手无策，而群智能优化算法的研究与应用则为解决这类问题提供了实用且有效的方法.如：Kar等[7]提出了一种基于引力搜索算法和粒子群算法的有效混合方法；刘三阳和靳安钊[8]提出了一种求解约束优化问题的协同进化教与学优化算法；Banaie-Dezfoul等[9]提出了一种狩猎策略的灰狼优化算法；肖子雅和刘升[10]提出了一种精英反向学习的黄金正弦鲸鱼算法；Nadimi-Shahraki等[11]提出一种基于维度学习狩猎搜索策略的改进灰狼优化算法；汪逸晖和高亮[12]提出一种引入动态感知概率、莱维飞行策略以及变异更新机制的改进乌鸦搜索算法.这些算法均被应用于求解工程约束优化问题，并取得了良好效果，但求解的多为几个经典老问题，种类较少且比较简单，解决工程设计优化问题仍需探索求解能力更强、寻优精度更高、稳定性和普适性更好的算法.

JAYA算法是2016年由Rao[13]提出的一种新型启发式智能优化算法，该算法控制参数少、易于实现，且具有趋优避差的导向性特征，很适于求解全局优化和工程设计优化问题，成为最近几年优化计算领域重要的研究和改进算法之一，已被成功应用于旅行商，文本聚类，特征选择，柔性车间调度，水电站水库优化调度等问题的求解之中.

虽然JAYA算法趋优避差的机制特点契合于复杂函数和工程设计中全局优化的思想和需求，但JAYA算法与其他基础性智能优化算法一样，其本身也存在着容易陷入局部极值、寻优精度有时不高和收敛速度较慢等问题.为此，许多学者针对JAYA算法的不足之处做了相应改进.Yu等[14]引入自适应惯性权重、基于经验的学习策略和混沌精英学习方法，提高了JAYA算法的寻优精度和稳定性.Kang等[15]将JAYA算法与支持向量机相结合，并成功应用于桥梁结构健康监测中的温度效应预测问题.Ingle等[16]引入莱维飞行和贪婪选择策略，丰富了JAYA算法种群的多样性，增强了算法的勘探能力，并成功应用于信道均衡问题.Iacca等[17]引入莱维飞行用于JAYA算法位置更新产生随机数，有效提高了算法跳出局部极值的能力.Zhao等[18]引入自适应学习策略，提高了JAYA算法的全局搜索能力，并成功应用于多目标混合零空闲置换流水车间调度问题.Kang等[19]构建了基于高斯过程代理模型的JAYA算法，并成功应用于混凝土坝动力参数反演分析，拓宽了JAYA算法的应用领域.Zhang等[20]引入局部开发和全局探索策略，有效增强了JAYA算法逃离局部最优的能力.Nayak等[21]引入变异策略，增强了JAYA算法全局收敛能力.Zhang 等[22–23]引入包含三种不同学习策略的综合学习机制来更新个体位置，提高了JAYA算法的全局搜索能力.

这些改进使JAYA算法在各自应用领域的优化性能得以提升，但JAYA算法求解全局优化和工程设计优化问题的能力仍有进一步改进的空间.本文提出一种面向复杂函数和工程设计优化问题的混合进化JAYA算法（Hybrid evolutionary JAYA algorithm, H-JAYA）.首先在计算当前最优和最差个体位置时引入反向学习机制，增强最优和最差个体跳离局部极值区域的可能性.然后在个体位置更新中引入并融合正弦余弦算子和差分扰动机制，不仅增加了种群的多样性，而且有效平衡和较好满足了算法在不同迭代时期对探索和挖掘能力的不同需求.最后采用奇偶不同的混合进化策略，有效利用不同演化机制的优势结果，进一步提高了算法的收敛性和精度.随后给出了算法流程伪代码，用理论分析证明了H-JAYA没有增加算法的时间复杂度.通过对基于多个不同寻优特征基准函数的CEC2017测试函数集套件进行多维度、多算法极值优化求解对比测试，结果表明，H-JAYA的收敛性能、寻优精度和求解稳定性均有明显提升，求解CEC2017复杂函数的效果相当优越，全局优化能力出色，非参数统计检验结果也显示了H-JAYA与其他对比算法的差异具有显著性.而对拉伸弹簧、波纹舱壁、管柱设计、钢筋混凝土梁、焊接梁和汽车侧面碰撞6个具有挑战性的工程设计约束优化问题的求解，也显示了HJAYA算法在处理不同类型工程优化设计问题时有着明显的优越性和适应性.

1 改进算法 H-JAYA

1.1 基本 JAYA 算法

Step1 设置算法初始参数：种群个体数量N、最大进化代数Max_iter、个体维度D，并在寻优范围内随机生成每个个体的初始位置xi(i=1,2,…,N).

Step2 根据目标函数计算种群个体的适应度值f(xi).

Step3 根据种群中个体的适应度值f(xi)，找出最好和最差适应度值fmin和fmax，并记录其位置xbest和xworst.

Step4 由式(1)对个体每一维的位置进行更新.

Step5 由目标函数f(x)求出新个体的适应度值，并对新旧解进行对比，若新解较优，则替换上代的个体位置，否则保留原来的个体位置.

Step6 判断当前迭代次数t是否达到最大迭代次数，若t≤Max_iter，返回 Step2；

Step7 确定最终的最优值并输出.

1.2 引入反向学习机制

JAYA算法中种群的当前最优和最差位置具有重要作用，用来引导种群个体向全局最优解进化，但若种群的当前最优和最差位置陷入局部极值区域，就容易导致群体出现搜索停滞的现象，无法获得更优的全局最优解.基于以上原因，将反向学习机制引入到JAYA算法的当前最优和最差位置中.

本文使用的反向学习机制是将基本反向学习与随机反向学习相融合，使JAYA算法种群中当前最优和最差个体位置随机进行基本反向学习或随机反向学习，从而增强最优和最差个体跳离局部极值区域的可能性，更好地引导JAYA算法种群寻找到全局最优解.而只对个体位置更新计算中起关键作用的当前最优和最差个体进行反向学习而不是对所有个体再逐一进行反向学习，既有利于避免JAYA算法陷于局部最优，又不至于影响算法的收敛速度.引入反向学习机制的数学模型如下：

其中：η为[0,1]之间均匀分布的随机数，rand为[0,1]之间均匀分布的随机数，Xmax和Xmin分别为种群中个体位置空间的上界和下界.xbest(t)和xworst(t)分别是当前个体最优和最差位置，xbest(t+1)和xworst(t+1)分别是更新后的下一代个体最优和最差位置.

1.3 引入正弦余弦算子和差分扰动机制

基本JAYA算法，采用了一个统一的位置更新公式，机制清晰简单、易于实现，且具有趋优避差的导向性特征，对一些问题有着较好的寻优效果.但对于一些复杂多极值优化问题，由于缺少不同迭代时期需要不同全局探索和局部挖掘能力与平衡的机制，导致算法前期的全局搜索有时不够充分，容易陷入局部极值，而后期则存在最优解附近局部精细挖掘能力不强的问题，造成算法有时寻优精度不高和收敛速度较慢的情况.为此，在JAYA算法的个体位置更新中引入并融合正弦余弦算子和差分扰动机制，正弦余弦算子通过迭代自适应因子和正弦余弦函数的变化改变JAYA算法中种群的个体状态，增加种群的多样性，并有效平衡和较好满足了算法在不同迭代时期对探索和挖掘能力的不同需求.差分扰动机制源于差分进化算法的变异思想，通过引入差分扰动，可以增强算法的局部搜索能力，提高收敛速度，而采用的双随机差分策略也较好保持了种群的活跃性，降低算法陷入局部极值的风险.将上述两种机制产生的位置更新公式通过转换概率m4，分别对应于算法的全局搜索和局部搜索阶段，有效提高了算法的寻优精度和收敛性能，数学模型如下：

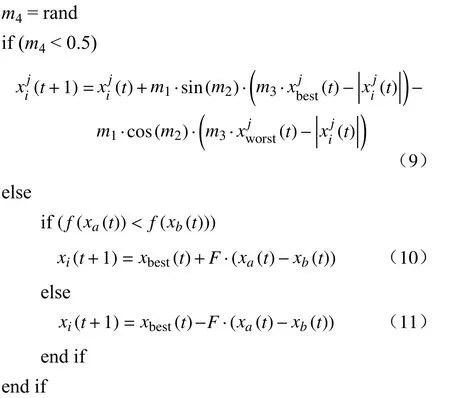
其中：m4为[0,1]之间均匀分布的随机数，是当前全局最优位置的第j维值，为当前全局最差位置的第j维值，xij(t)是当前代中第i个个体在第j维的位置值，xij(t+1)是更新后下一代中第i个个体在第j维的位置值，xa、xb是种群中两个随机个体，满足a∈[1,N]和b∈[1,N]，且a≠b≠i，缩放因子F为[0,1]之间的D维随机向量.在正弦余弦算子机制中，控制搜索距离的参数m2为[0,π]之间均匀分布的随机数，控制距离对解影响的参数m3为[0,1]之间均匀分布的随机数，而对于控制搜索步长的迭代自适应因子m1，采用了带有随机性的非线性递减策略，其计算公式为：

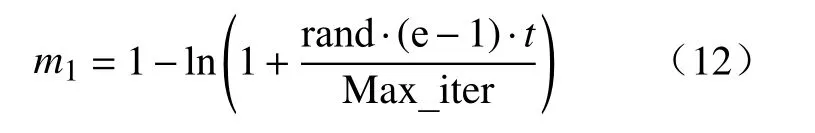
分析式(12)可知，m1起着平衡全局搜索和局部搜索能力的重要作用.在算法迭代前期，m1的值较大，全局搜索步幅较大，使算法具有较强的全局探索能力，而在算法迭代后期，m1的值较小，增加了算法在最优解附近区域深度挖掘的能力，提高了算法的收敛精度.而m1在保持从1到0整体非线性递减趋势的同时，也呈现出一定的随机性，这种随机性降低了算法如在中前期未能搜索到全局最优值附近，而在后期因控制因子的单调递减直接陷入局部极值无法跳出的风险.

1.4 奇偶不同的混合进化策略

为了更好发挥和融合改进前后两种不同JAYA机制的进化特点，采用奇偶不同的混合进化策略，具体描述为：当迭代次数为奇数时，使用融合正弦余弦算子和差分扰动的个体位置更新公式进行搜索；当迭代次数为偶数时，使用基本JAYA算法的个体位置更新公式进行搜索.同时，在这两种机制中都引入上面所述的反向学习机制，而且当更新后所产生个体的适应度值优于上一代个体的适应度值时，新的个体位置将被接受，否则按一定概率接受更新后的个体位置.接受概率p的计算公式为：

其中，缩放因子λ为[0,0.1]之间均匀分布的随机数，接受概率p利用e的负指数函数特性随迭代次数增加而非线性递减，在算法的迭代前期，接受概率p较大，可以接受较多的差解，有利于进化的多样性，随着迭代次数的增加，接受概率p不断减小，接受较差解越来越少，最后在接受概率p趋于0时，就不再接受任何较差解了，这在迭代后期有利于算法在最优值附近利用两种不同机制反复进行深度挖掘，提高了算法的收敛性和精度.

2 H-JAYA 算法流程与时间复杂度分析

2.1 H-JAYA 算法流程

根据新的适应度值比较并输出最优解位置

2.2 时间复杂度证明

时间复杂度是体现算法性能的关键因素，它反映了算法的运算效率.文献[24]和文献[25]分别对蝴蝶优化算法和萤火虫算法的时间复杂度进行了分析，本文采用同样的思想对H-JAYA算法的时间复杂度进行分析.

对于群智能优化算法而言，当算法的进化代数和种群大小取值在一个合理范围内时，再增加进化代数和种群大小的值，对提高算法的寻优能力和求解精度已基本没有作用，因此将迭代次数和种群规模设置为一个固定值是群智能优化算法求解问题时普遍采用的方法，而决定算法时间复杂度的基本要素就是代表问题规模的个体空间维度.

在基本JAYA算法中，若种群规模为N，个体位置的维度为n，设：设置初始参数的时间为t0，初始化JAYA算法个体位置中每一维的时间为t1，求给定目标函数适应度值的时间为f(n).则初始化种群阶段的时间复杂度为：

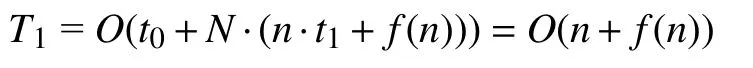
进入迭代后，总迭代次数为Max_iter.

在个体位置更新阶段，设：根据种群中个体的适应度值找出并记录最好和最差个体位置的时间为t2，产生均匀分布随机数r1、r2的时间分别为t3，由式(1)对个体位置每一维进行更新的时间为t4.则该阶段的时间复杂度为：

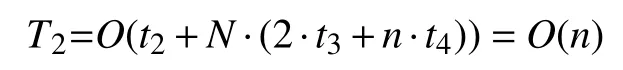
在边界处理和新旧解比较阶段，设：每个个体每一维边界处理的时间为t5，计算新个体适应度值的时间为 f(n)，新旧解适应度值的比较替换的时间为t6，则此阶段的时间复杂度为：

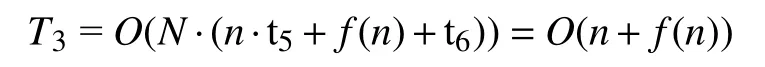
综上所述，基本JAYA算法总的时间复杂度为：

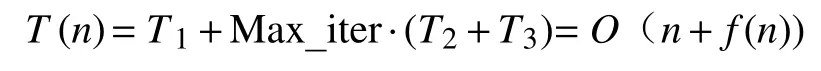
在H-JAYA改进算法中，算法的种群规模N、个体维度n、参数设置时间、初始化种群和求给定目标函数适应度值的时间均与基本JAYA算法一致，两者初始化过程一样，因此H-JAYA算法在初始化种群阶段的时间复杂度与基本JAYA算法相同，为：

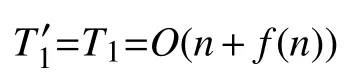
进入迭代后，总迭代次数仍为Max_iter.

根据种群中个体的适应度值找出并记录最好和最差个体位置的时间仍为t2，设：由式(2)求sign(η)的时间为 ε1，由式(3)、式(6)分别对最优解、最差解进行反向学习的时间均为ε2，分别对反向学习前后新旧最优解、最差解进行比较替换的时间均为ε3，用式 (13)产生接受概率p的时间为ε4，则这一阶段的时间复杂度为：

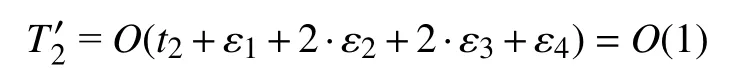
在迭代次数为奇数时的个体位置更新阶段，设：由式 (12)产生m1的时间为ε5，m2、m3和转换概率m4都是均匀分布的随机数，产生它们的时间分别为t3，设m4<0.5执行全局搜索的个体数k(0≤k≤N)，由式(9)对个体位置每一维进行更新的时间为ε6；而m4≥0.5执行局部搜索的个体数为N–k，此时，从种群中随机选取两个个体的时间为ε7，计算这两个随机选取个体适应度值的时间分别为f(n)，比较这两个个体适应度值的时间为t6，用式(10)或(11)对个体位置进行更新的时间为ε8，则这一阶段的时间复杂度为：

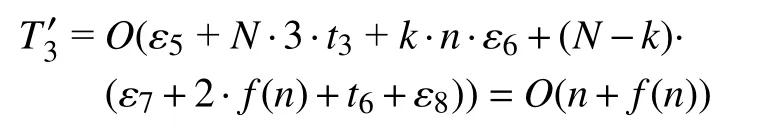
在迭代次数为奇数时的边界处理和新旧解比较阶段，每个个体每一维边界处理的时间、计算更新后个体适应度值的时间、新旧解适应度值的比较替换时间均与基本JAYA算法在边界处理和新旧解比较阶段的时间一致，故该阶段的时间复杂度为：

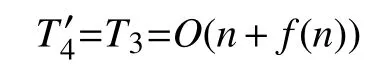
在迭代次数为偶数时的个体位置更新阶段，产生均匀分布随机数r1、r2的时间分别为t3、由式(1)进行每一维个体位置更新的时间仍为t4.故该阶段的时间复杂度为：

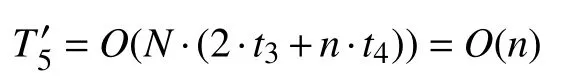
在迭代次数为偶数时的边界处理和新旧解比较阶段，每个个体每一维边界处理的时间、计算更新后个体适应度值的时间、新旧解适应度值的比较替换时间均与迭代次数为奇数时的边界处理和新旧解比较阶段相同.故该阶段的时间复杂度为：

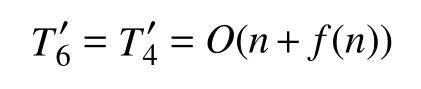
综上所述，H-JAYA算法总的时间复杂度为：

由此可知，改进算法H-JAYA和基本JAYA算法的时间复杂度相同，没有降低算法的运行效率.

3 仿真实验

为了全面检验改进算法H-JAYA的寻优能力，本文的仿真实验分为两部分进行.3.1节将算法在CEC2017测试函数集[26]上进行多维度函数极值优化测试，用以验证算法的寻优性能与收敛能力.3.2节研究了6个具有挑战性的工程设计约束优化问题，用以检验算法在不同类型工程优化设计问题上的求解能力和应用潜力.两部分实验都将本文算法H-JAYA与基本JAYA算法(2016)[13]、Improved JAYA Optimization Algorithm(IJAYA, 2017)[14]、Comprehensive Learning Jaya Algorithm（CLJAYA,2020）[22–23]、鲸鱼优化算法（WOA, 2016）[5]和 Hybrid Firefly and Particle Swarm Optimization Algorithm（HFPSO, 2018）[27]共 6 种性能优越的代表性算法进行了对比实验.

为了保证实验的公平性与客观性，6种对比算法采用相同的软、硬件平台在相同条件下独立运行50次，运行环境为Windows10、编程语言为MATLAB R2019a，种群大小均为30，最大进化代数Max_iter=1000.算法参数设置方面，4种JAYA类算法无需另设参数，而WOA算法只需设置用于定义对数螺旋的常数b=1，HFPSO算法中学习因子c1与c2均为1.49445，这些参数的取值都与各自算法的原文献和源代码取值相同.

3.1 函数极值优化仿真实验

3.1.1 寻优精度分析

本文对CEC2017测试集中30个函数都进行了测试和分析，因篇幅限制下面只讨论按序给出的混合测试函数f11(x)、f12(x)、f19(x)和f20(x)，组合测试函数f21(x)、f22(x)、f25(x)、f26(x)、f29(x)和f30(x)，其他函数的测试结果与之类似，不再一一赘述.

表1统计了6种算法分别在10维、50维和100维时，对于不同测试函数各自独立运行50次，得到的最佳值、平均值和方差.

由表1的数据可以看出，除个别函数外，改进算法H-JAYA在各函数不同维度下的求解精度和稳定性均明显优于其他5种对比算法，显示出HJAYA算法对于JAYA机制改进的显著性和有效性.

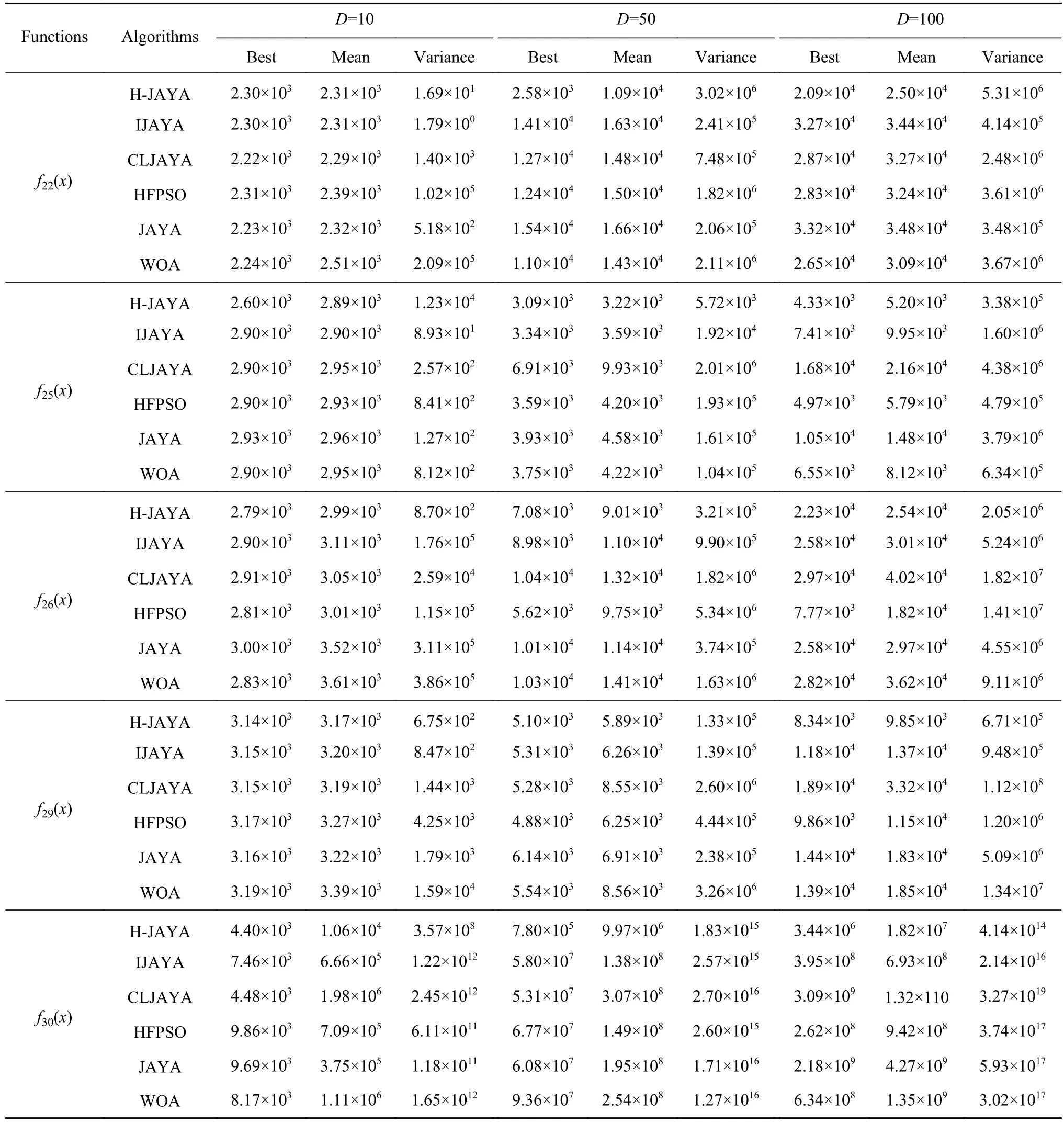
表1 (续)Table 1 (Continued)

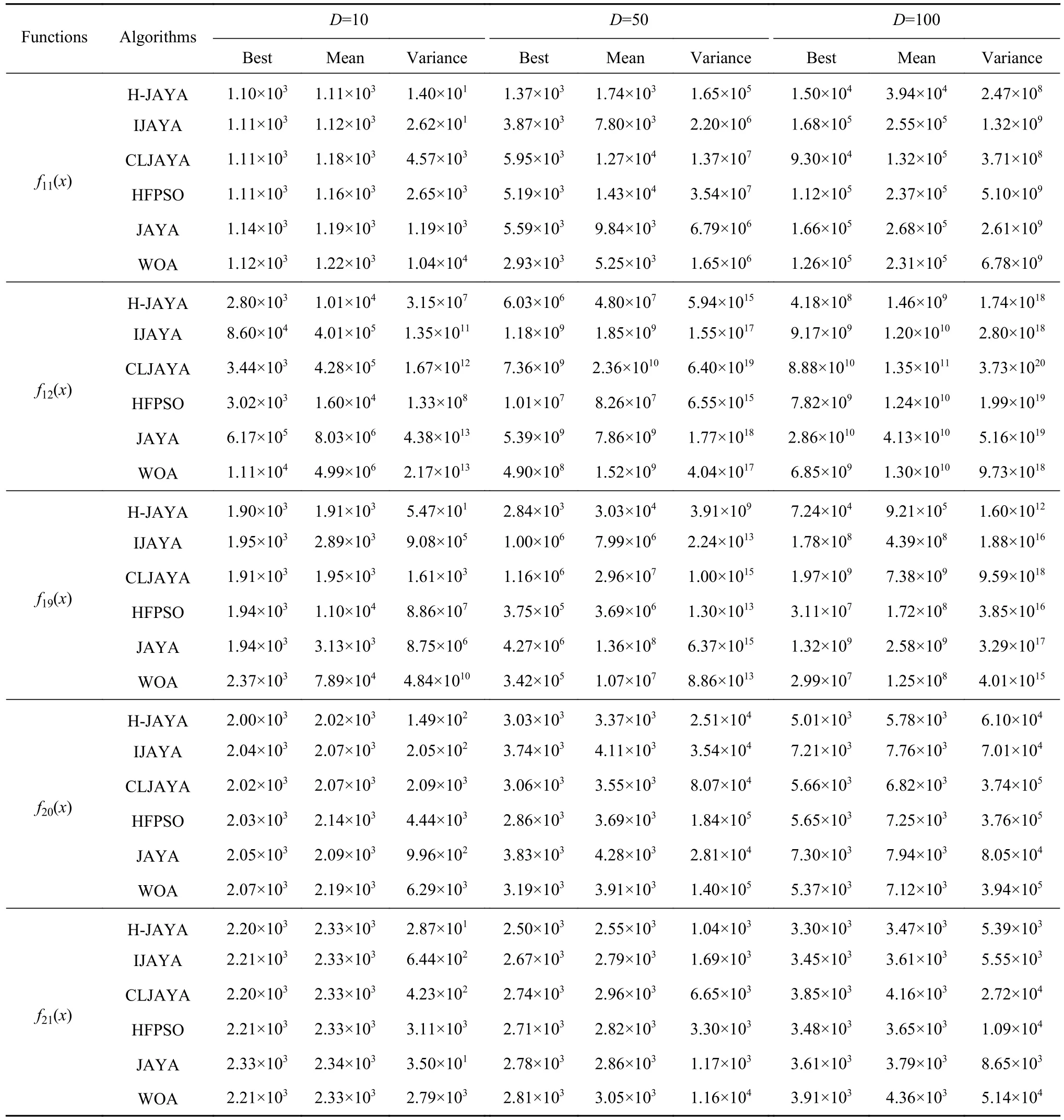
表1 6 种算法在固定迭代次数下的寻优结果比较Table 1 Comparison of the optimization results of six representative algorithms under fixed iteration times

在10维条件下，对于函数f11(x)、f19(x)和f20(x)，H-JAYA在这3个函数上的寻优结果最佳值均为理论最优值，求解效果十分出色；CLJAYA、IJAYA、JAYA、HFPSO和WOA算法的最佳值、平均值和方差都差于H-JAYA算法.对于函数f11(x)、f26(x)、f29(x)和f30(x)，H-JAYA在这4个函数上的最佳值、平均值和方差虽未达到理论最优值，但全部优于其他5种算法，求解能力明显突出和优越.对于函数f21(x)，H-JAYA的最佳值与CLJAYA算法相同，优于其他4种算法，平均值与CLJAYA、IJAYA、HFPSO和WOA算法相同，优于基本JAYA算法，而且方差是6种算法中最小的.对于函数f22(x)，H-JAYA的最佳值与IJAYA算法相同，略逊于WOA、JAYA和CLJAYA算法，优于HFPSO算法，平均值与IJAYA算法相同，略逊于CLJAYA算法，优于其他3种算法，方差略逊于IJAYA算法，优于其他4种算法.对于函数f25(x)，H-JAYA的最佳值和平均值均优于其他5种算法，方差略逊于其他5种算法.

在50维和100维的高维条件下，6种算法的求解精度都会随着维度的增加有所降低，但相较于其他5种算法，H-JAYA算法仍表现出良好的寻优精度和稳定性.在50维条件下，对于函数f11(x)、f12(x)、f19(x)、f21(x)、f25(x)和f30(x)， H-JAYA 在 这6个函数上的最佳值、平均值和方差都优于其他5种算法.对于函数f22(x)，H-JAYA的最佳值和平均值都优于其他5种算法，方差略逊于其他5种算法.对于函数f20(x)、f26(x)和f29(x)，H-JAYA 在这3个函数上的最佳值略逊于HFPSO算法，优于其他4种算法，平均值和方差优于5种对比算法.在100 维条件下，对于函数f11(x)、f12(x)、f19(x)、f20(x)、f21(x)、f25(x)、f29(x)和f30(x),H-JAYA在这 8个函数上的最佳值、平均值和方差均优于其他5种算法，表现出优越的高维求解能力.对于函数f22(x)，HJAYA的最佳值和平均值都优于其他5种算法，方差略逊于其他5种算法.对于函数f26(x)，H-JAYA的最佳值和平均值略逊于HFPSO算法，但方差优于该算法，而且H-JAYA的最佳值、平均值和方差均优于其他4种算法.

以上求解结果和分析表明，相比于5种寻优性能较为优秀的代表性对比算法，H-JAYA算法整体呈现出更为优越的求解性能，较好解决了JAYA算法在求解复杂函数全局优化时易陷入局部极值、寻优性能不稳定，寻优精度不高的问题.

3.1.2 收敛曲线分析

一个算法性能的优劣，可以直观地通过收敛曲线展现出来，收敛曲线显示了算法在寻优过程中陷入局部最优的次数和收敛速度.下面给出对于 3.1.1节f21(x)、f22(x)、f25(x)、f26(x)、f29(x)和f30(x)共6个求解难度较大的组合函数的收敛曲线图，其他函数的收敛曲线对比结果与之相似，不再一一赘述.图1是6种算法在维度D=100时对于这6个函数的收敛曲线对比图.

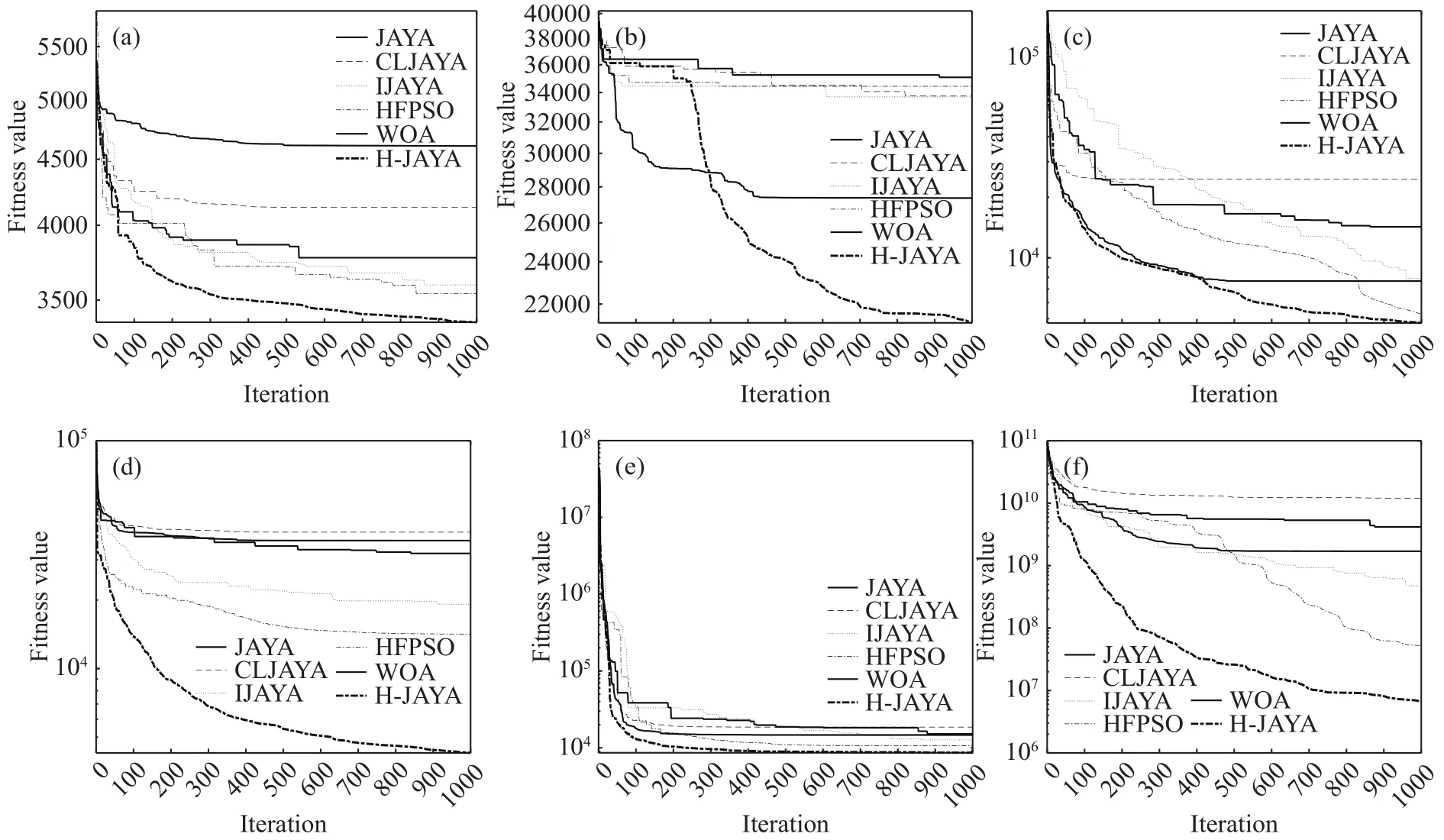
图1 收敛曲线.(a) f21(x); (b) f22(x); (c) f25(x); (d) f26(x); (e) f29(x); (f) f30(x)Fig.1 Convergence curves: (a) f21(x); (b) f22(x); (c) f25(x); (d) f26(x); (e) f29(x); (f) f30(x)

以上图1清晰地展现了H-JAYA、JAYA、CLJAYA、IJAYA、WOA和HFPSO算法在进化过程中适应度值的变化趋势.从这些图中可以看出HJAYA收敛速度快于其他5种算法，且收敛曲线也总体比较光滑，陷入局部极值的次数较少，寻优能力较强.

在图1(a)中，CLJAYA和WOA算法收敛速度一直慢于JAYA，更明显慢于H-JAYA；IJAYA在迭代前期收敛速度略慢于JAYA，160代以后则快于JAYA，但一直明显慢于H-JAYA；HFPSO收敛速度在迭代前期与JAYA互有快慢，260代以后则快于JAYA，且在迭代早期快于H-JAYA，但在60代以后明显慢于H-JAYA.在图1(b)中，CLJAYA收敛速度在迭代前期与JAYA十分相近，在480代以后快于JAYA，但始终明显慢于H-JAYA；IJAYA收敛速度一直快于JAYA，且在迭代前期略快于H-JAYA，但在280代以后明显慢于H-JAYA；WOA收敛速度一直明显快于JAYA，且在迭代前期快于H-JAYA，但在300代以后，随着H-JAYA收敛速度加快，WOA已明显慢于H-JAYA；HFPSO收敛速度一直快于JAYA，且在迭代前期快于H-JAYA，但在290代以后则明显慢于H-JAYA.在图1(c)中，CLJAYA收敛速度前期快于JAYA，但在170代以后慢于JAYA，更是一直明显慢于H-JAYA；IJAYA收敛速度在迭代前期慢于JAYA，570代以后快于JAYA，但一直明显慢于H-JAYA；WOA收敛速度一直明显快于JAYA，且在迭代早期与H-JAYA相近，但在50代以后随着H-JAYA收敛速度加快，WOA慢于H-JAYA；HFPSO收敛速度在迭代前期与JAYA相近，在200代以后明显快于JAYA，但始终慢于H-JAYA.在图1(d)中，CLJAYA和WOA算法收敛速度慢于JAYA，更明显慢于H-JAYA；IJAYA和HFPSO算法收敛速度快于JAYA，但明显慢于HJAYA.在图1(e)中，CLJAYA收敛速度在迭代前期快于JAYA，460代以后却相近并最终慢于JAYA，更是始终慢于H-JAYA；IJAYA收敛速度在迭代前期与JAYA快慢交替基本相近，530代以后则快于JAYA，但一直慢于H-JAYA；WOA收敛速度从迭代开始到880代一直快于JAYA，880代以后与H-JAYA相近，但始终慢于H-JAYA；HFPSO收敛速度在迭代前期慢于JAYA，100代以后则快于JAYA，但一直慢于H-JAYA.在图1(f)中，CLJAYA收敛速度慢于JAYA，更明显慢于H-JAYA；IJAYA、WOA和HFPSO算法收敛速度一直快于JAYA，但都慢于H-JAYA.

综上所述，本文提出的H-JAYA算法在低、中、高三种维度下对于具有较高求解难度的CEC-2017测试函数集都有较好的寻优性能，其求解精度、收敛速度和寻优稳定性均优于JAYA、CLJAYA、IJAYA、WOA和HFPSO等5种代表性对比算法，表现出较为显著的求解优越性.

3.1.3 实验结果的秩和检验统计分析

为了验证改进算法H-JAYA与其他对比算法在实验结果上的差异具有显著性，进一步评价算法的寻优性能，采用非参数统计检验方法–Wilcoxon秩和检验，进行统计分析.表2给出了对于CEC2017测试函数集套件，H-JAYA分别与其他对比算法在D=100时求解3.1.1节具有代表性的10个函数的统计检验结果.其中，用符号“+”、“–”和“=”分别表示H-JAYA的寻优结果优于、劣于和相当于其他对比算法.由文献[28]可知，那些p<0.05的结果就可被认为是拒绝零假设具有显著性的有力验证.

从表2的统计检验结果来看，改进算法H-JAYA与JAYA、IJAYA、CLJAYA、WOA和HFPSO算法相比，在全部10个函数上的检验p值都小于0.05且符号为“+”，拒绝零假设.由此可见，H-JAYA与其他5种对比算法的计算结果之间具有显著差异，且H-JAYA显著更优.

表2 各算法求解 CEC2017 测试集套件 Wilcoxon 秩和检验的 p 值Table 2 p-value for Wilcoxon’s rank-sum test on each algorithm used to solve the CEC2017 test suite

3.2 H-JAYA 求解工程设计约束优化问题

为了检验改进算法H-JAYA求解工程约束优化问题的能力，将H-JAYA算法和上述5种代表性对比算法应用于拉伸弹簧、波纹舱壁、管柱设计、钢筋混凝土梁、焊接梁和汽车侧面碰撞6个工程优化设计问题.这6个工程问题具有各自不同的约束条件和求解难度，能够很好地测试出各算法求解工程设计优化问题的能力和适用性.在求解这些工程优化问题时，将每种算法独立运行50次，得到设计结果的最佳值、平均值和方差作为评价各算法求解能力的指标.

3.2.1 求解拉伸弹簧设计问题

拉伸弹簧设计是一个最小化约束问题，其目的是设计一种重量最轻且满足挠度、剪切应力、波动频率、外径4个约束条件的拉伸弹簧.该问题包含3个设计变量，分别是线径x1(0.05≤x1≤2.00)、平均线圈直径x2(0.25≤x2≤1.30)、活性线圈数量x3(2.00≤x3≤15.0).该设计问题的数学模型如下：

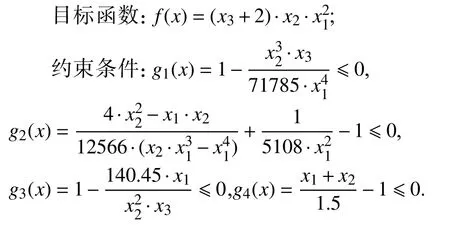
表3是改进算法H-JAYA和其他5种对比算法各自独立运行50次求解拉伸弹簧设计问题得到的最佳值、平均值和方差.从表中数据可以看出，H-JAYA算法的最佳值、平均值和方差都优于其他5种算法，表现出较优的求解能力和稳定性.

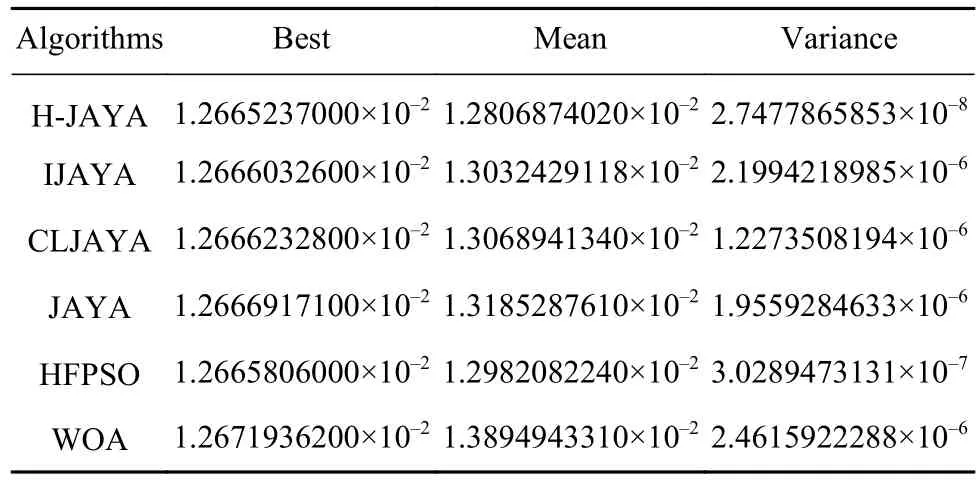
表3 6种算法求解拉伸弹簧设计问题的寻优结果比较Table 3 Comparison of the optimization results of six representative algorithms used to solve the tension/compression spring design problem

3.2.2 求解波纹舱壁设计问题

波纹舱壁设计问题的目标是最小化波纹舱壁的重量，该问题包含6个约束条件和4个设计变量，设计变量分别是波纹舱壁的宽度x1(0≤x1≤100)、波纹舱壁的高度x2(0≤x2≤100)、波纹舱壁的长度x3(0≤x3≤100)、波纹舱壁的厚度x4(0≤x4≤5)，其数学模型如下：

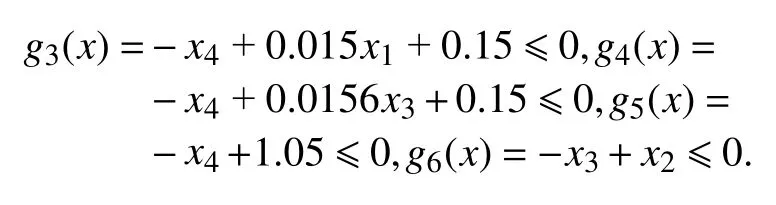
表4是6种算法50次求解波纹舱壁设计问题得到的最佳值、平均值和方差.由表中数据可知，H-JAYA算法的最佳值与IJAYA、CLJAYA算法相同，且优于其余3种算法，而平均值和方差则优于所有5种对比算法，表现出更好的寻优精度和稳定性.

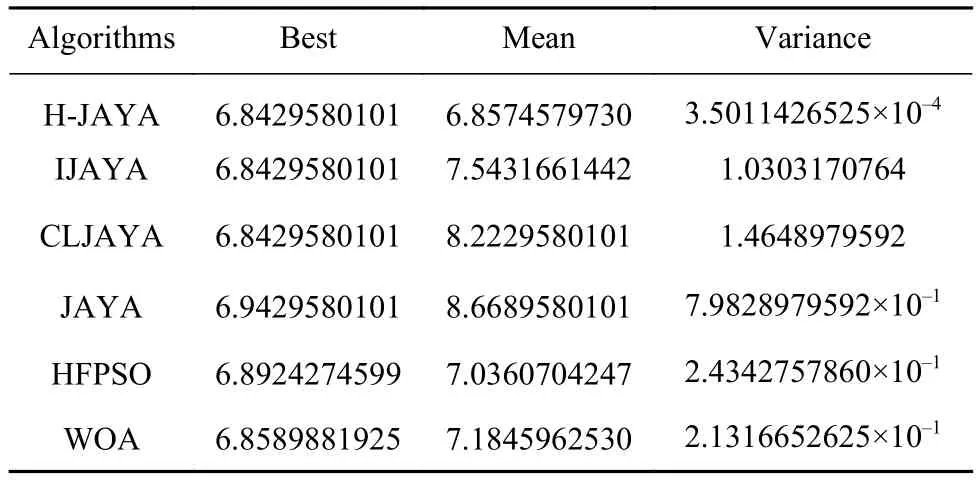
表4 6种算法求解波纹舱壁设计问题的寻优结果比较Table 4 Comparison of the optimization results of six representative algorithms used to solve the corrugated bulkhead design problem

3.2.3 求解管柱设计问题

管柱设计问题的目标是以最低成本设计一个均匀的管状截面柱来承载压缩载荷，该设计问题包含6个约束条件和2个设计变量，设计变量分别为管柱的平均直径x1(2≤x1≤14)，管壁的厚度x2(0.2≤x2≤0.8)，其数学模型如下：

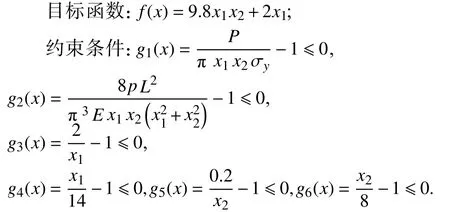
其中：管柱弹性模量E=0.85×106，屈服强度 σy=500.

表5是6种算法求解管柱设计问题时得到的最佳值、平均值和方差.由表中数据可以清楚地看出，H-JAYA算法的最佳值与CLJAYA相同，且优于其余4种算法，而平均值和方差则优于其他全部5种算法，展现出更为优越的寻优能力和求解稳定性.

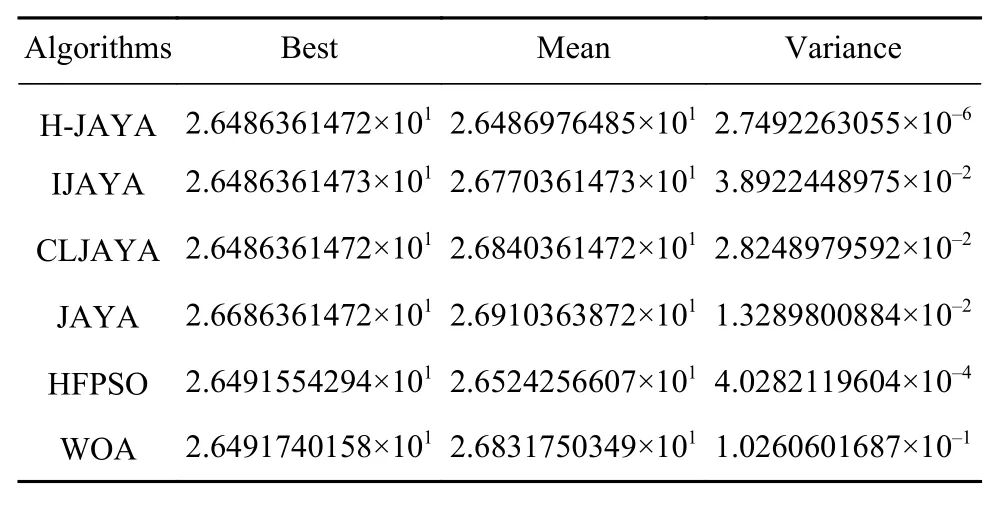
表5 6种算法求解管柱设计问题的寻优结果比较Table 5 Comparison of the optimization results of six representative algorithms used to solve the tubular column design problem

3.2.4 求解钢筋混凝土梁设计问题

钢筋混凝土梁是用钢筋混凝土材料制成的梁，其形式多种多样，是房屋建筑、桥梁建筑等工程结构中最基本的承重构件，应用范围极广.该问题的目标是以最低成本设计一个有最大承载力的钢筋混凝土梁，问题中包含2个约束条件和3个变量，这些变量分别是钢筋的面积梁的长度其数学模型如下：

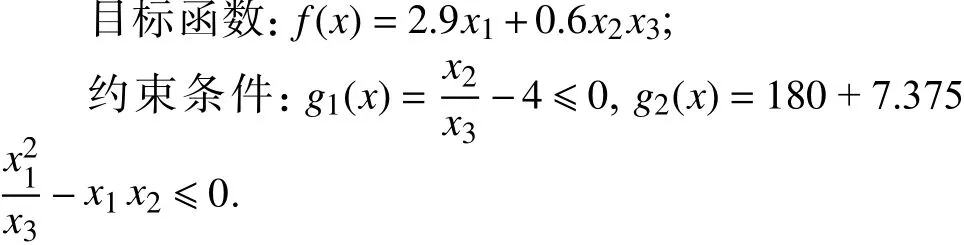
表6统计了6种算法运行50次求解钢筋混凝土梁设计问题得到的最佳值、平均值和方差.由表中数据可知，H-JAYA算法求得的最佳值、平均值和方差都是6种算法中最好的，求解性能更加出色.

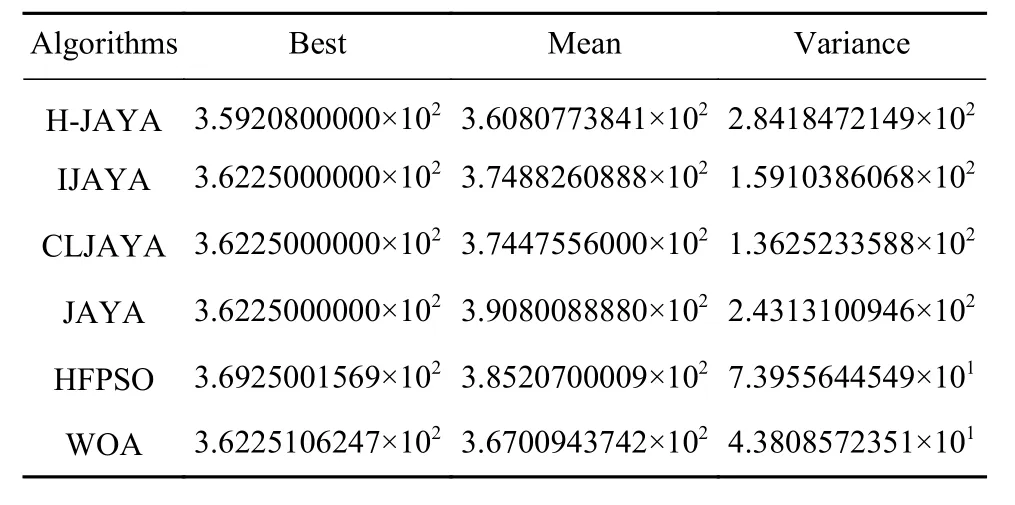
表6 6种算法求解钢筋混凝土梁问题的寻优结果比较Table 6 Comparison of the optimization results of six representative algorithms used to solve the reinforced concrete beam design problem

3.2.5 求解焊接梁设计问题

焊接梁设计的目标是在剪切应力、弯曲应力、屈曲载荷、端部挠度和侧面约束下找到最低制造成本.该问题有7个约束条件和4个设计变量，设计变量分别是焊缝厚度x1(0.125≤x1≤2)、焊缝长度x2(0.1≤x2≤10)、梁宽度x3(0.1≤x3≤10)、梁厚度x4(0.1≤x4≤2)，剪切应力τ，横梁弯曲应力σ，屈曲载荷Pc，横梁挠度δ以及各设计变量之间的尺寸约束，具体数学模型如下：

表7统计了6种算法求解焊接梁设计问题得到的最佳值、平均值和方差.观察表中数据可以看出，改进算法H-JAYA的最佳值、平均值和方差都是6种算法最好的，而且H-JAYA算法50次寻优结果的最佳值与文献[29]中给出的最优值相同，达到理论最优，求解效果相当出色.

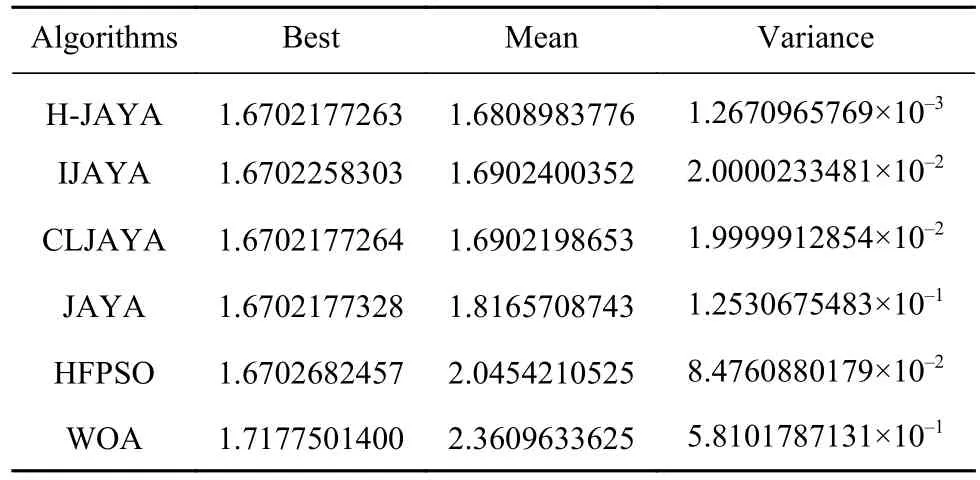
表7 6种算法求解焊接梁设计问题的寻优结果比较Table 7 Comparison of the optimization results of six representative algorithms used to solve the welded beam design problem

3.2.6 求解汽车侧面碰撞设计问题

汽车侧面碰撞设计问题的目标是研究车门部件对汽车侧面碰撞安全性的影响，通过改进汽车的结构，以最大限度地提高汽车的碰撞安全性，从而降低交通事故的伤害.该问题包括11个设计变量和10个约束条件，设计变量分别是B柱的内板厚度x1(0.5≤x1≤1.5)、B柱的加强板厚度x2(0.5≤x2≤1.5)、车顶横梁长度x3(0.5≤x3≤1.5)、B柱的外板材料屈服强度x4(0.5≤x4≤1.5)、门槛梁长度x5(0.5≤x5≤1.5)、抗侧撞梁长度x6(0.5≤x6≤1.5)、车顶边梁长度x7(0.5≤x7≤1.5)、B柱的内板材料屈服强度x8(x8∈{0.192,0.345})、车底部横梁长度x9(x9∈{0.192,0.345})、碰撞位置最小角度x10(x10≥−30)、碰撞位置最大角度x11(x11≤30)，具体数学模型如下：

表8统计了6种算法50次求解汽车侧面碰撞设计问题得到的寻优结果最佳值、平均值和方差.从表中数据可以看出，H-JAYA算法的最佳值、平均值和方差都是6种算法最好的，表现出优越的求解能力和稳定性.

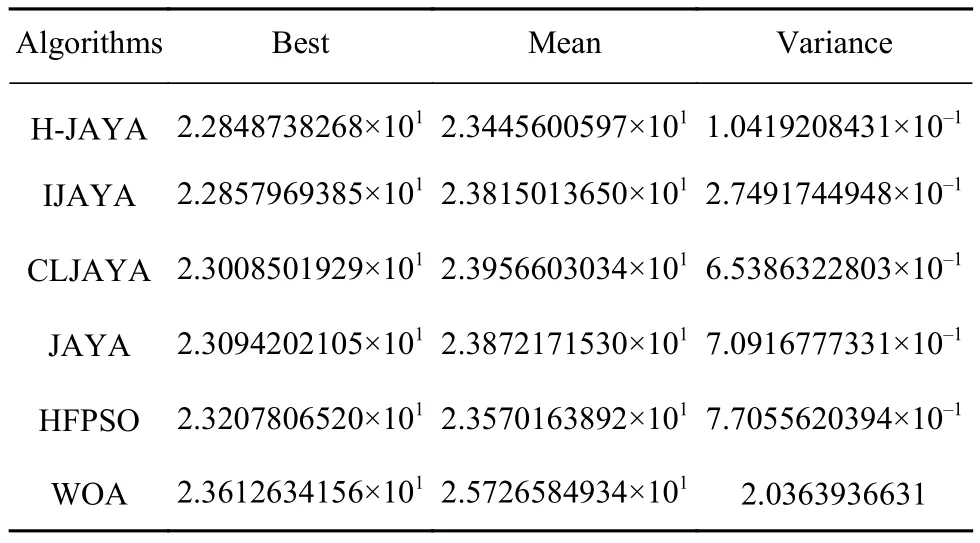
表8 6种算法求解汽车侧面碰撞问题的寻优结果比较Table 8 Comparison of the optimization results of six representative algorithms used to solve the car side impact design problem

以上求解结果分析以及相关文献[30–32]的求解结果都表明，智能优化算法对于求解工程设计约束优化问题是有效的，而本文所使用的代表性对比算法在求解工程问题时都具有良好的求解性能，其中改进算法H-JAYA在面对不同类型和复杂程度的工程优化设计问题时，更是展现出十分优越的求解精度和稳定性，对于求解工程设计约束优化问题有着明显可见的优越性和适用性.

4 结论

本文提出一种面向全局优化的混合进化JAYA算法H-JAYA，在最优和最差个体位置中引入反向学习机制，增强了算法跳离局部极值区域的能力；引入正弦余弦算子和差分扰动机制对个体位置进行更新，不仅增加了种群的多样性，而且较好平衡了算法的全局探索和局部挖掘能力；在算法结构上采用奇偶不同的混合进化策略，使算法的收敛性和精度得到了进一步提高.理论分析证明该算法的时间复杂度与基本JAYA算法相同，没有降低执行效率.将H-JAYA算法应用于CEC 2017复杂函数的全局优化求解中，其50次运行得到的寻优结果最佳值、平均值和方差明显优于其他5种性能优越的代表性对比算法；而Wilcoxon 秩和检验则验证了H-JAYA算法与各对比算法之间的优势差异具有显著性.最后，将该算法成功运用于6个工程设计优化问题，取得了很好的优化效果.上述研究表明，H-JAYA算法可以获得更好的全局搜索和局部搜索能力，算法的寻优能力具有明显的优越性，求解全局复杂函数和工程设计约束优化问题有着显著的可行性和有效性.在后续的研究中，考虑将改进的JAYA算法应用到更多实际问题求解中，以进一步验证算法性能，完善算法的改进机制，拓宽和提高算法的应用领域与能力.