软体机械臂的建模与神经网络控制

杨 妍，刘运鹏，韩江涛，刘志杰1,✉，韩志冀

1) 北京科技大学智能科学与技术学院，北京 100083 2) 北京航天自动控制研究所，北京 100070 3) 北京科技大学自动化学院，北京 100083

机械臂在家庭机器人、工厂流水作业、航天工程等生产生活领域有着重要的应用，它能帮助人们完成重复、危险的任务，减少了生产周期和人力成本.随着机械臂工作环境的非结构化发展，人们对机械臂的环境适应性以及灵活性提出了更高的要求.然而普通刚性机械臂因其结构刚度大、灵活性差、安全性能差、功率高等特点，难于满足非结构环境下的任务需求.为了解决这一问题，研究者们提出了超冗余机械臂的概念[1]，通过增加机械臂的关节以及连杆的数目来使刚体机械臂能够适应非结构化的环境以及处理特殊的任务.但是这类机械臂仅仅增加了运动的自由度，机械结构仍是刚性的.而且自由度越高，制造工艺和逆动力学的求解更加复杂，这一特点限制了它们的应用.受到自然界一些软体动物以及柔性组织的启发，研究者们提出了软体机械臂这一概念.这类机械臂不再具有离散的关节和连杆，而是通过模仿蛇、章鱼等生物的运动，通过柔软材料制造的连续体装置来实现更加灵活的运动[2].比刚性机械臂、多冗余机械臂更加柔软、灵活，在医疗服务[3]、灾难救援[4]、以及工业生产[5]等方面有着非常广阔的应用前景.

软体机械臂有着近乎连续的机械特点以及独特的驱动方式，因而软体机械臂的建模一直是软体机械臂研究中的一个难点.目前主流的软体机械臂建模方法主要有三种：有限元方法建模[6–8]，Cosserat梁建模[9–11]，分段恒曲率方法建模[12]（Piecewise constant curvature，PCC）.基于有限元方法对软体机械臂建立的模型复杂且难以进行控制器设计.基于Cosserat梁方法建立出的模型是一类偏微分方程，这种模型精度非常高，能够适应于许多不同结构的软体机械臂.但是其最后得到的偏微分方程同样难以被用于控制目的.分段恒曲率建模方法相比于其他方法推导简单且仿真容易实现，但是该模型在软体机械臂有较大外部载荷的情况下，恒曲率的假设就难以成立，模型会造成较大误差.

目前分段恒曲率（PCC）方法是当下最流行的软体机械臂建模方法，PCC将梁进行一系列的参数化，从而对梁进行描述.文献[13]和[14]针对分段恒曲率方法进行了一定的拓展与改进.文献[15]在PCC模型的基础上引入的扭转分量，有效的提升了模型在有较大外部载荷时的精确度.这种参数化的思想也被拓展到Cosserat梁里面.文献[16]首次提出了分段恒应变的建模方法（Piecewise constant strain，PCS），这种方法建立出的模型考虑了软体机械臂的剪切力与扭力，因而在软体机械臂有较大外部载荷时有更好的表现.

本文在分段恒应变模型的基础上，做出了一定的改进，不再假定软体机械臂每个横截面有相同的应变，而是根据一定的模式沿着软体机械臂逐渐减小，提高了模型的整体精度.但因为不再假定软体机械臂横截面的应变恒定，对模型的建立造成一定的困难.

目前关于软体机械臂的控制往往采用开环控制或者简单的反馈控制.文献[17]针对软体机械臂提出了基于PCC逆运动学的形状反馈控制算法，控制精度不高.文献[18]利用相机标定技术和目标识别技术，利用PCC逆动力学模型和图像雅可比矩阵反推驱动空间的驱动力配置，实现了软体机械臂的视觉伺服控制.文献[19]介绍了基于拉格朗日动力学建模的方法和非线性的控制策略，提出了逆动力学控制和滑模控制,达到了一个比较理想的状态.但是由于软体机械臂的无穷维自由度，上述模型并不能精确的给出其动力学模型导致了控制不精确.而且软体机械臂模型往往存在一些未知的动态信息，有必要对不确定项进行估计，而神经网络[20–22]可以逼近任意的非线性函数，使得它成为了自适应未建模动态的有效方法.文献[23]提出了新型自适应控制处理了系统参数的不确定性.此外神经网络还可以与Back-Stepping方法相结合应用于各种高阶复杂系统的控制问题[24].

本文研究了一类线驱动软体机械臂的建模和控制.首先把软体机械臂当作一个Cosserat梁建立一个偏微分方程，然后结合Ritz方法[25]对软体机械臂应变场进行离散化，就得到常规常微分形式的动力学模型.进一步采用反向传播(Back propagation，BP)神经网络得到形状空间与驱动空间驱动力的映射关系.然后，利用径向基函数（Radial basis function，RBF）神经网络估计了模型中存在的未知动态，将自适应神经网络控制器应用到建立的模型.最后通过仿真实验验证了模型和控制器的有效性.

1 动力学建模

1.1 模型示意图

线驱动的软体机械臂制作简单，它的结构简图如图1所示.线驱动软体机械臂的主体材料一般使用硅胶制成，再在其中插入若干根驱动线，通过控制驱动线的长度来控制机械臂做出各种动作.

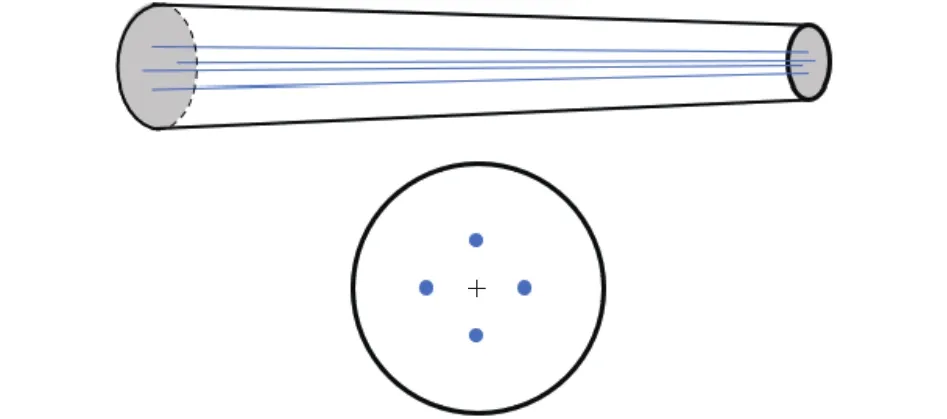
图1 软体机械臂结构简图Fig.1 Structure diagram of a soft manipulator

1.2 连续软体臂模型

软体机械臂的主体可以视为一个弹性杆，工程上一般利用Cosserat梁来描述该弹性杆的运动，Cosserat梁的原理是将弹性杆分成很多段，每一段可以视为梁的一个横截面，梁的剪切变形使横截面与中心线不再正交，此时的挠性线曲率不仅因截面打孔，而且因梁的剪切变形而改变如图2所示.软体机械臂的每一个横截面可以用X∈[0,1]来进行表示，X为杆的长度，最远端为1，最近端为0.

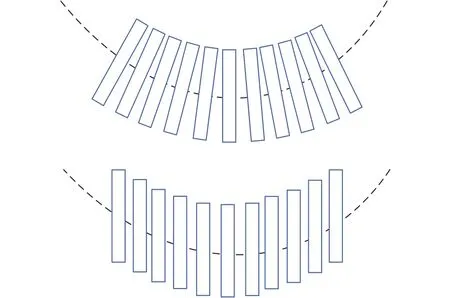
图2 弹性梁横截面转动变形（上）与剪切变形（下）以及 2 种变形的挠性线Fig.2 Elastic rotation deformation (up) and shear deformation (down)and related flexible lines

在三维空间中，软体臂不仅可以做平移运动还可以做旋转运动，软体臂的姿态需要用一个六维的向量来描述.该空间向量由三维的欧式空间位置向量和三维的欧拉角向量组成.在本文中使用六维的欧几里得群表示每一个横截面在空间中的姿态：

其中，R∈SO(3)代表横截面在空间中的旋转姿态，r∈R3代表横截面在欧式空间中的位置.这样整个梁的姿态空间可以被定义为：

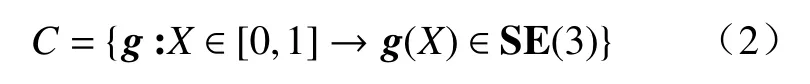
其中，SE(3)是欧式变换矩阵.由于软体机械臂会随着时间的变化而不断变化，因此这里的g也依赖于时间t[26].在本文中，使用“点”和“撇”代表对于时间t的偏导数和对X的偏导数.场g的时间和空间的变化可以使用两个向量η和ξ进行表示：

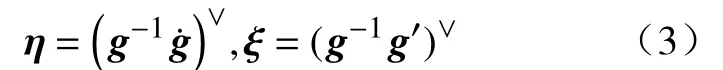
同时，由式（3）通过简单的变形可以得到：

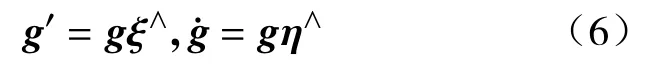
机械臂横截面的惯性张量M和胡克张量H定义如下:

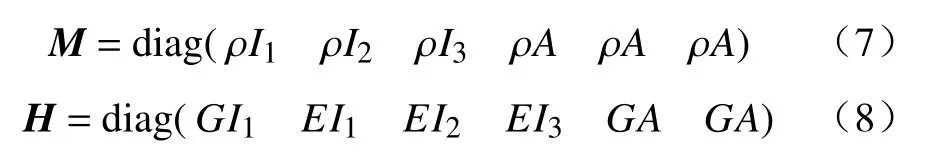
其中，ρ代表软体机械臂主体材料的密度，A代表软体机械臂的横截面的面积，I代表横截面转动惯量，E代表弹性模量，G代表剪切模量.GI，EI，EA，GA是材料的抗扭刚度、剪切刚度、抗拉压刚度和弯曲刚度.

软体机械臂的横截面的动量 Σ和应力 Λ可以分别表示为：

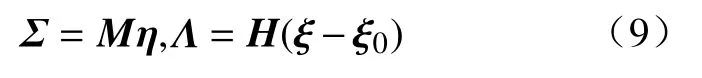
其中， ξ0代表软体机械臂的内部能量为零时软体臂的应变.利用哈密顿原理基于系统的动能 Πk(t)，势能 Πp(t)，和功 Πw(t)来导出机械系统的运动方程：

其中，δ是变分算子，t1和t2是两个时间常数.对于软体臂系统，动能来源于材料粒子和刚体的平移运动.保守力场（如重力）中的材料应变和运动产生势能.控制力，干扰力和力矩构成了功，进而用变分法和分步积分得到软体机械臂的偏微分方程：

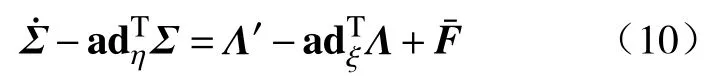
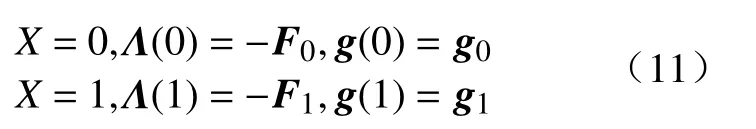
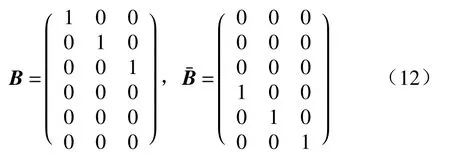
可以将 ξ变成如下的形式：

其中，

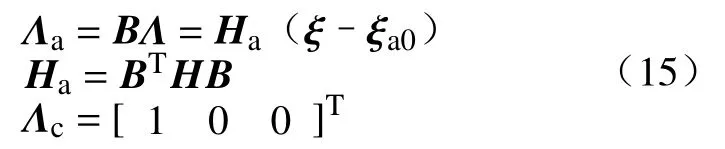
根据式（15），已经得到了软体机械臂内部的应力与其弹性形变的关系.在实际情况下，没有外部驱动力时，软体机械臂的应力还与软体机械臂材料的黏度有关.在考虑材料黏度的情况下，软体机械臂应力的可变部分可以表示为：

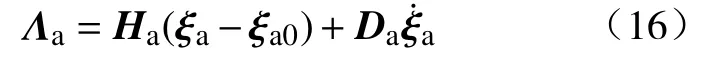
其中， ξa0是 ξa的 初始值，Da=BTDB,D是软体机械臂材料的黏度矩阵.一般情况下，可以使用下面的式对Da进行近似计算:

这里的 µ是一个系数，可以取 µ =10−3.

现在可以得到在没有施加外界驱动力的情况下，软体机械臂内的应力与其形状之间的关系.接下来需要考虑在有外界驱动力的情况下，软体机械臂内部应力的变化.对于线驱动的软体机械臂，可以通过控制穿过整个软体机械臂内部的驱动线的长度来控制机械臂的形状.设由于软体机械臂驱动线长度的变化而造成的机械臂内部应力的变化为 Λad，此时机械臂的内部应力可写为：

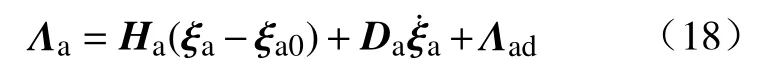
在不考虑摩擦力的情况下，可以认为，机械臂驱动线的所做功等于应力 Λad做的功：

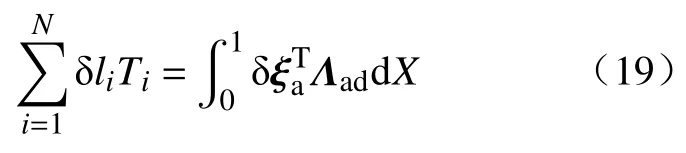
其中，N是软体机械臂驱动线的数目，li为第i根驱动线的长度，δli为第i根 驱动线的变化量，Ti为第i根驱动线上的张力， δ ξ为机械臂应变的变分δξ=(δKT，δΓT)T， δ ξa= δK.接下来需要计算出驱动线长度的变化量.机械臂的驱动线与机械臂横截面的交点为P(X)=(0,PY(X),PZ(X))T，这里的P(X)是根据软体机械臂驱动线的布线方式来决定的，表一给出了一些常用的布线方式所对应的P(X).表中Rb代表了机械臂的直径.

表1 驱动线布线方式与 P (X)关系表Table 1 Relationship between the driving wire and P(X)

由此可以得到驱动线与横截面的交点在参考坐标系下的坐标为：

将 φi对 位 置X的 导 数 φi′表示为同一根驱动线与相邻横截面交点的变化量：

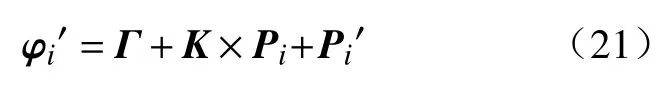
由此驱动线的长度和长度的变化量可以表示为：

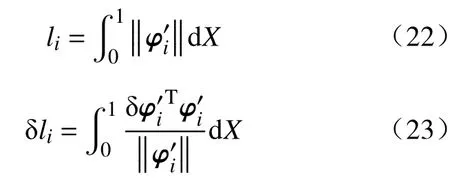
将式（21）带入式（23）可得：

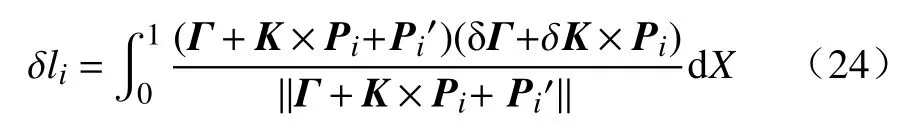
将上式带入式（19）经过化简可得到机械臂由于驱动线变化而造成的内部应力变化的表达式：

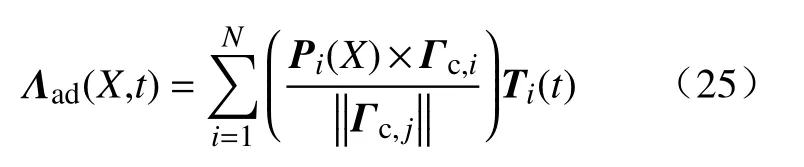
以上建立了机械臂内部应力与形状和驱动力之间的关系的模型，下面根据机械臂的应变还原机械臂的形状.式（6）第一项g′=gξ∧中的g′可以表示相邻两个横截面之间位置的变化，由此可见只要知道机械臂的初始位置g0以及整个机械臂的各个横截面的应变 ξ，便可还原整个机械臂的形状.为了方便计算，可以使用四元数Q∈R4来替换g=(R,r)中的旋转矩阵R，此时g′=gξ∧将转换为如下的形式：

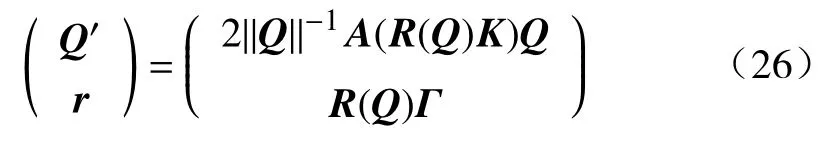
其中，A(K)是一个运算符，其代表的运算如下：

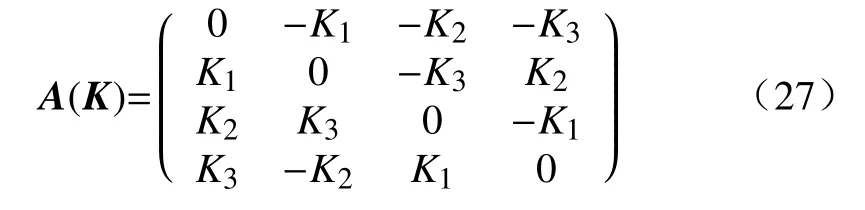
1.3 离散软体臂模型

这里因为不假定机械臂的每个横截面的应变是不变的，因此在机械臂移动的时候，机械臂的应变不仅与时间t有关，还与在机械臂上所处的位置X关，为了解决原始的偏微分模型难于设计控制的问题，可以使用Ritz方法对应变进行离散化，Ritz方法的基本思想是利用一组已知的多项式的组合来对函数进行近似：

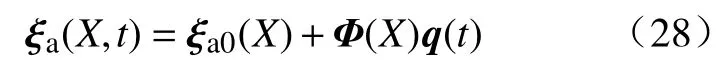
式中的 Φ (X)为被选择的一组多项式，在机械臂中也可以被称为形状方程，这表明可以用关于时间的应变广义坐标函数q(t)来表示某个时刻软体机械臂的整体形状.

本文中选择：

使用q可以还原整个机械臂各个横截面的应变，但是这也造成了模型高度的非线性.q的每一维在几何上的所代表的意义都无法说明，这就对进一步求解模型的各个参数造成了困难.为了解决这样的困难，可以采用数值的方法求解模型的各个参数.使用牛顿–欧拉逆动力学算法，通过给算法特定的输入，即可在每一个时间循环中求解出模型所需要的参数（见附录）.在软体机械臂中，由于不存在关节，所以实际上求出的是机械臂横截面上的应力.

首先求出软体机械臂上的各个关节的速度和加速度.根据式（3）应用混合偏导数式，=可以得到软体机械臂横截面的应变与速度之间的关系：

求导得：

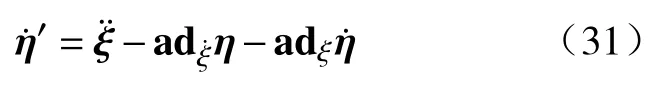
应用式（29）和（30）就可以在知道机械臂某一端速度的情况下求出整个机械臂所有横截面的速度和加速度.

接下来需要根据已知的机械臂的横截面速度和加速度求解出横截面上的应力.将式（9）的第一项带入式（10）即可得到机械臂内部应力与速度之间的关系：

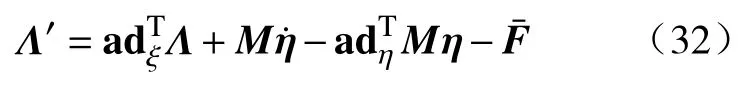
由于用Ritz方法对应变进行了离散化，在形状空间中的广义力与应力的关系如下：

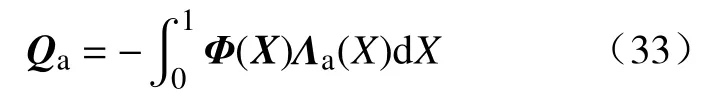
在本文中，研究的机械臂为一端固定的软体机械臂，可以设 η ==0，通过逆动力学算法可以得到其拉格朗日形式的动力学模型：

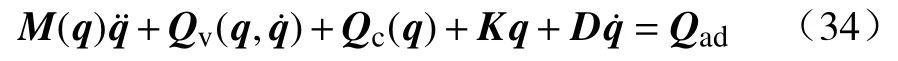
其中，M(q)是软体臂的惯性矩阵，¨为广义加速度，Qv(q,˙)包含全部的速度依赖力，其中包括科里奥利力和离心力，Qc(q)包含配置依赖的外力，比如重力，Kq是形状空间里的广义的恢复力，˙是在形状空间里面的广义阻尼力.上述三个矩阵可由牛顿–欧拉逆动力学得出数值解，数值解的具体步骤可参考[27].Qad是形状空间中由驱动线的运动所造成的广义力，可以由式（25）通过一定的转换得到：

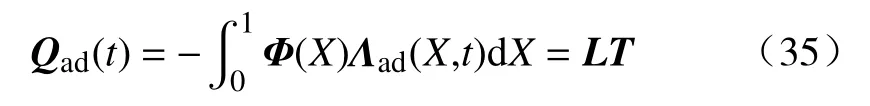
这里L是一个n×N的控制矩阵，T∈iN是由所有驱动线上的张力组成的向量,其中，

至此，得到了最终的软体机械臂的动力学模型.

2 基于 RBF 神经网络的控制器设计

2.1 问题描述

本次设计考虑的是一端固定的软体机械臂，同时考虑了模型的不确定项，为了方便设计，写出其状态空间表达式：

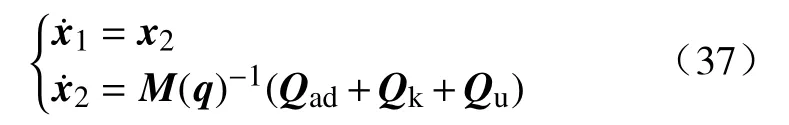
其 中 ，x1=q，x2=˙，Qk=−(Qv+Qc+Kq+˙)表示模型中已知的部分.系统的输出为：

假设1.所有的变量都是有界的，即|Qu|≤Qumax，∀x1∈Rn.

假设2.Qu为光滑函数.

2.2 RBF 神经网络

RBF神经网络可以以任意精度逼近任意的非线性函数，由于其具有良好的近似功能，所以这里用其来近似模型中的不确定项Qu.

假设有一连续函数f(x)，可用RBF神经网络近似表述为：

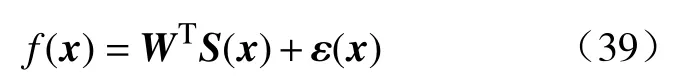
其中，x∈Rn为输入向量，W∈Rm×n为权重矩阵，ε(x)是径向基神经网络的逼近误差，S(x)=[s1(x),s2(x),···,sn(x)]T，si(x)是径向基函数，采用如下的高斯径向基函数

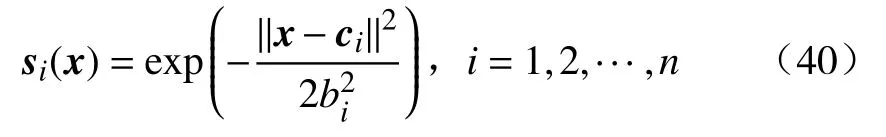
其中，ci,bi分别是第i个神经元的中心位置和宽度.

为了保证RBF神经网络逼近的有效性和准确性，进行如下假设：

假设3.存在一个最优权重矩阵W*，对任意给出的小的正数 γ，系统的逼近误差 ς均满足：

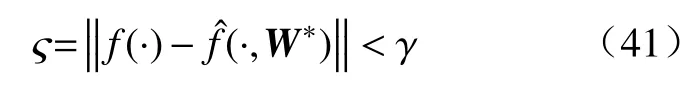
2.3 神经网络控制器的设计

记参考输入为yd，定义跟踪误差为：

其中，yd连续且可导.

则e1的导数可以表示为：

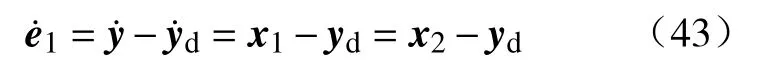
选取如下形式的李雅普诺夫函数：

对V1两边求导可得：

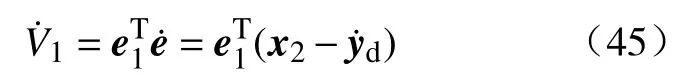
定义：

则有x2=e2+α，其中 α 代表虚拟控制器.

把式（46）代入式（45）可以得到：

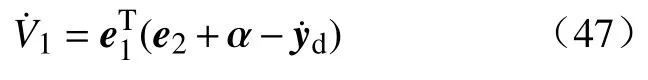
虚拟控制器 α 可设计为：

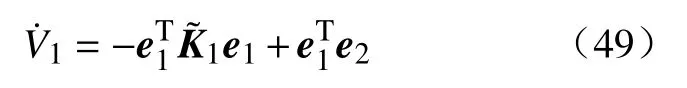
可以看到如果e2=0，则≤0.

选取如下李雅普诺夫函数：

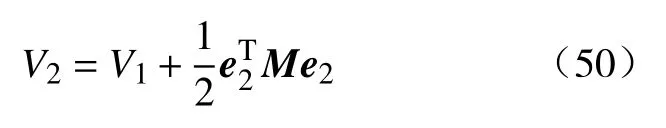
其中，M为正对角阵，将（46）和（49）代入（50）可得：

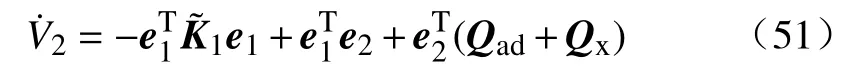
其中，Qx=Qk+Qu−M

接下来用RBF神经网络逼近含有未知项的参数：

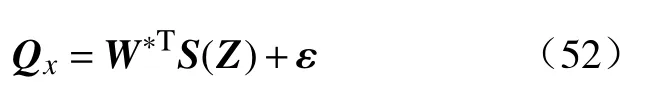
其中，Z=，W∗为未知的神经网络的理想权重矩阵，用来估计W∗，ε代表神经网络的近似误差，满足如下条件：

这里提出软体机械臂的控制律和神经网络权值矩阵更新法则：

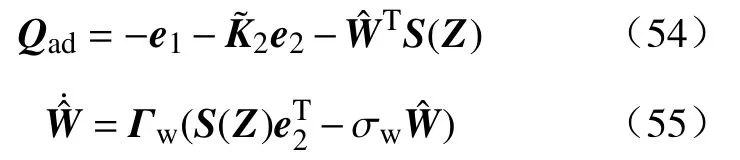
定理：考虑软体机械臂系统(37)，控制输入(54)、虚拟控制(48)和RBF权重矩阵更新律(55)，有如下结论:

如果满足假设1～3，那么系统中所有参量(,e1,e2,S(Z))都是有界的，并且状态量 (e1,e2)会收敛到0的一个小邻域内.

证明：选取如下的李雅普诺夫函数：

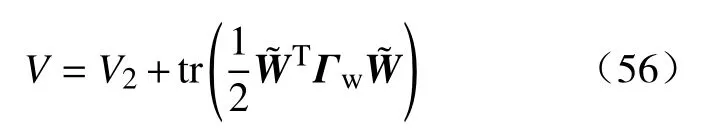
对式（56）求导并带入控制(54)和权重矩阵更新律(55)可得：

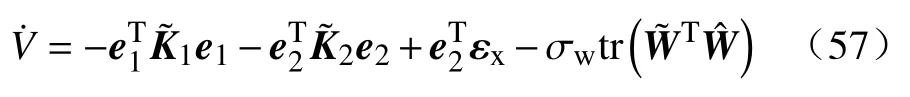
可以得到：

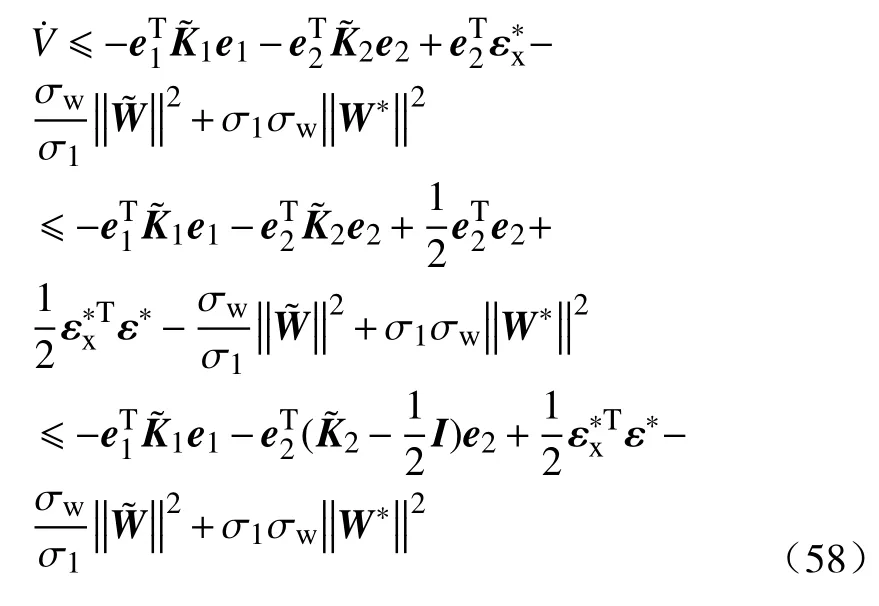
可以进一步将式（58）化简为：

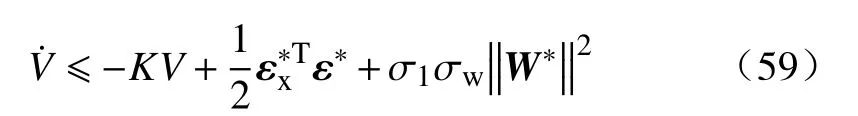
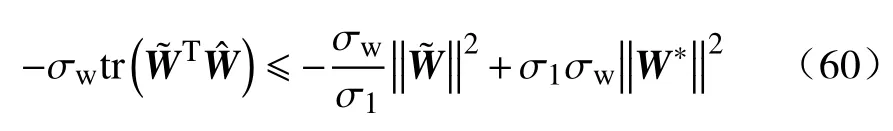
通过对（59）变换可得：

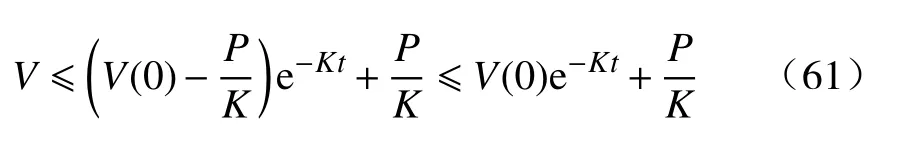
这里，式（59）～（61）表示计算过程中的额外项加和，记为P，根据式（44）和（50）可以得到：

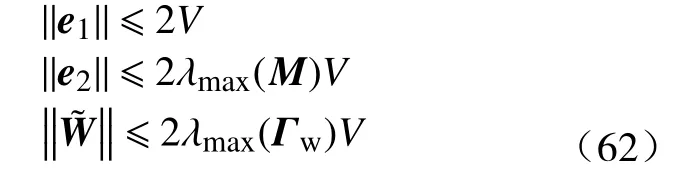
从上式可知，闭环系统为半全局一致有界.从式（61）、（62）可以知道V是有界的，从而e1，e2是有界的，对于所有的Z,S(Z)也是有界的因此控制输入Qad也是有界的，所(以闭环系)统的所有信号都是有界的.通过调节,σw增大K使V减小，进而即跟踪误差e1在tend时刻后，收敛到0的小邻域内.

2.4 基于 BP 神经网络的驱动力转换

上一节得到了控制输入Qad，还需要将形状空间的广义驱动力Qad转换到驱动器空间的驱动力T，可以根据式（35）对驱动矩阵L求逆得到，但是由于驱动矩阵L是一个奇异矩阵，无法通过简单的矩阵求逆得到驱动线上张力的大小.由于神经网络对 任意非线性函数有比较好的逼近效果，所以 选择BP神经网络解决这个问题.

通过给软体机械臂的驱动线不同的张力，根据模型（34）可以在给驱动线施加以不同规律变化的张力T，记录下所能产生的广义驱动力Q.在获取5000组数据之后，以广义驱动力Q作为输入，驱动线的张力作为输出搭建BP神经网络，应用梯度下降算法训练，可以使用该网络根据形状空间的驱动力Qad获取当前驱动线上施加的张力T.

3 数值仿真验证

数值仿真验证分为两部分，一部分来验证基于Ritz方法推导的模型的有效性，其中建模方法的合理性可见[28]，第二部分来验证设计的控制策略的合理性，两者都基于MATLAB仿真平台.

3.1 模型验证

表2列出了软体机械臂的物理参数.

表2 软体机械臂的物理参数Table 2 Physical parameters of the soft manipulator

在使用Ritz方法对机械臂应变进行离散化时，即（29）式中n为5，机械臂的初始速度、加速度和初始应变均为0.机械臂的固定段的位置：

假设软体机械臂末端不受外界的力F1=[00 0000]T，机械臂整体不会在运动过程中受到来自外界环境的力即¯=0.

首先，需要验证模型的有效性，通过给机械臂的驱动线施加不同的张力，来验证机械臂是否可以按照预期中弯曲.在实验中采用的布线方式为平行布线，设定T=[1 0 2 0]T（单位：N）,软体机械臂稳定状态下的形状示意图如图3所示.

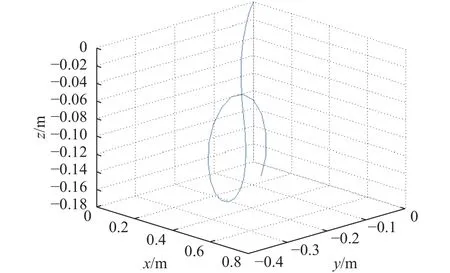
图3 在外力 T 下软体机械臂的稳定状态Fig.3 Steady state of the soft manipulator under the external force T

从图4中可以看出，前文中所建立的模型在给定绳子的张力之后可以仿真得到合理的机械臂形状.

下面验证驱动线不同的布线方式对运动方式的影响.给定每条驱动线输入的张力T=[T10 0 0 ]T，仿真时间为5 s，其中T1随时间的变化关系为：

从图4～6中可以看出，模型针对各种布线方式都能够达到理想的仿真效果.通过比较各个模型的仿真结果，可以看出，在给驱动线施加相同的力的情况下，平行布线的机械臂的弯曲程度最高，收束布线的软体机械臂的弯曲程度略低，交叉布线的机械臂形状随着驱动线张力的增加逐渐变成“S”形.在实际的应用中可以根据不同的需求选择合适的软体机械臂布线方式.

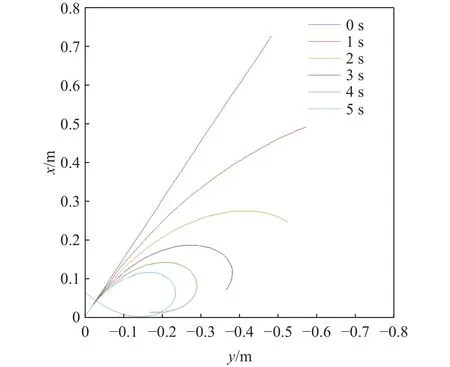
图4 平行布线下软体机械臂形状变化图Fig.4 Shape change of the soft manipulator under parallel wiring

3.2 BP 神经网络仿真

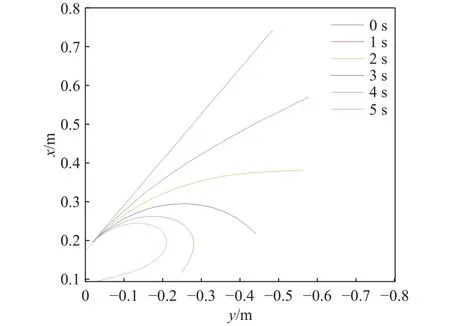
图5 收束布线下软体机械臂形状变化图Fig.5 Shape change of the soft manipulator under converging wiring

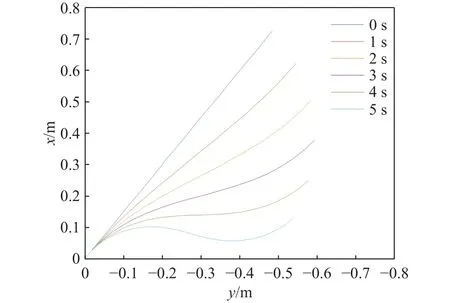
图6 交叉布线下软体机械臂形状变化图Fig.6 Shape change of the soft manipulator under cross wiring

这里选择3层结构的BP神经网络，其中隐藏层的神经元数量为8个.搭建神经网络和训练均使用Matlab自带的神经网络工具箱进行操作.神经网络误差设定为平方误差，初始学习率10−3，训练目标为误差小于10−8.图7给出了神经网络误差的变化情况:

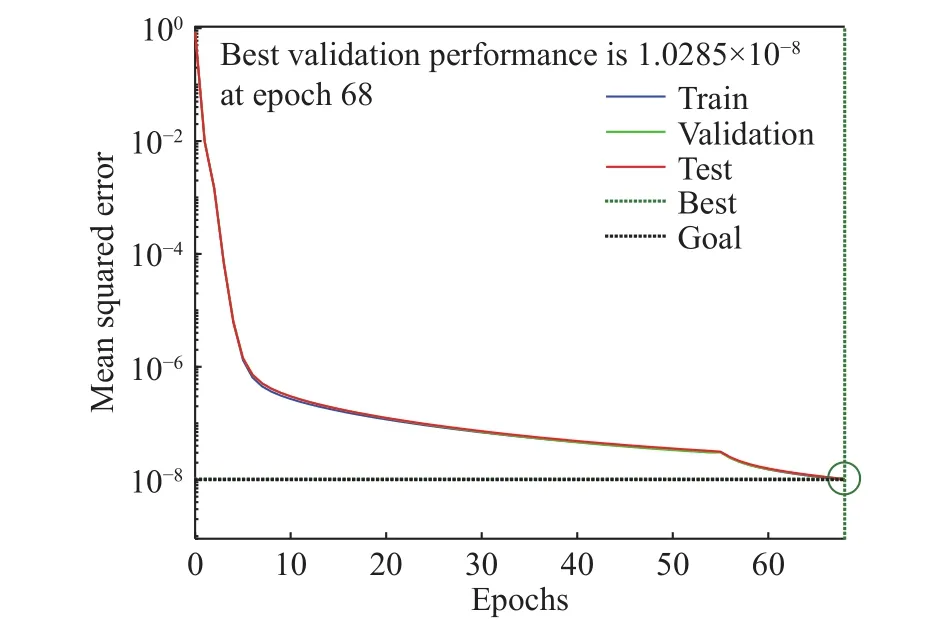
图7 BP 神经网络训练近似误差图Fig.7 BP neural network training approximate error

可以看出，经过一段时间的训练，BP神经网络就可以在较小的误差内将形状空间的广义驱动力转化为驱动空间绳子的驱动力.

3.3 跟踪效果仿真

先要确定软体机械臂整个运动过程中的动作，由于软体机械臂的高自由度，要对机械臂的运动过程进行轨迹规划.确定好机械臂运动过程中的一些姿态，应用五次多项式插值的方法，确定整个运动过程机械臂的运动轨迹，确保软体机械臂能够在运动过程中保持平稳.在本文建立的软体机械臂模型中，Ritz法离散化后的广义应变坐标共有十五维，需要对机械臂广义应变坐标的每一维进行多项式插值操作，之后，设定的控制目标如下：

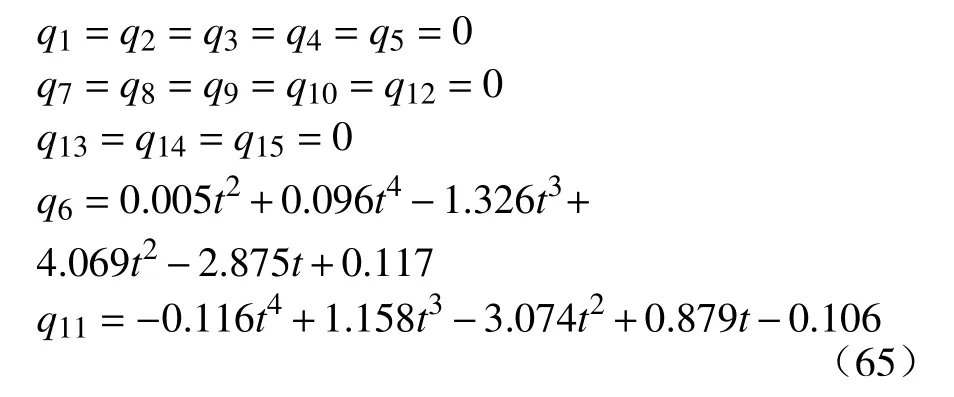
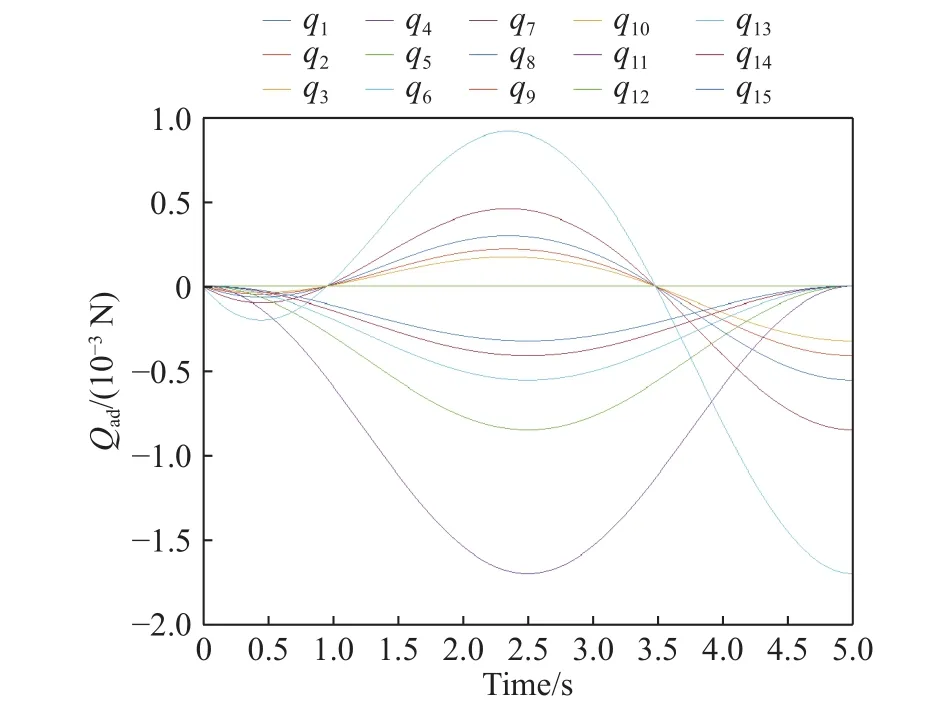
图8 广义驱动力随时间变化图Fig.8 General force variation diagram

利用之前训练好的神经网络，将广义驱动力作为输入，可以得到软体机械臂驱动线张力的变化图(图9).从图10中可以看出系统的跟踪误差在最初的一秒内迅速减少，在之后能够使误差保持在一个相对较小的范围内，如图11所示表明软体机械臂能较好得沿着期望的轨迹进行运动.

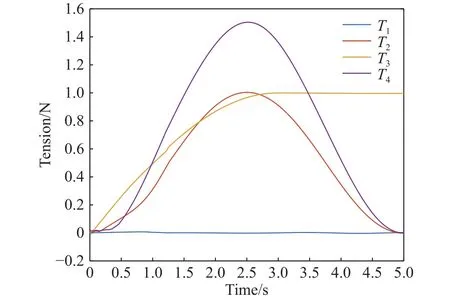
图9 驱动线张力随时间变化图Fig.9 Line force variation diagram

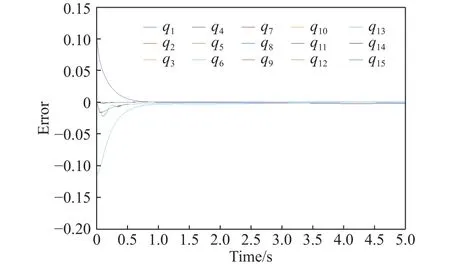
图10 跟踪误差变化图Fig.10 Tracking error graph

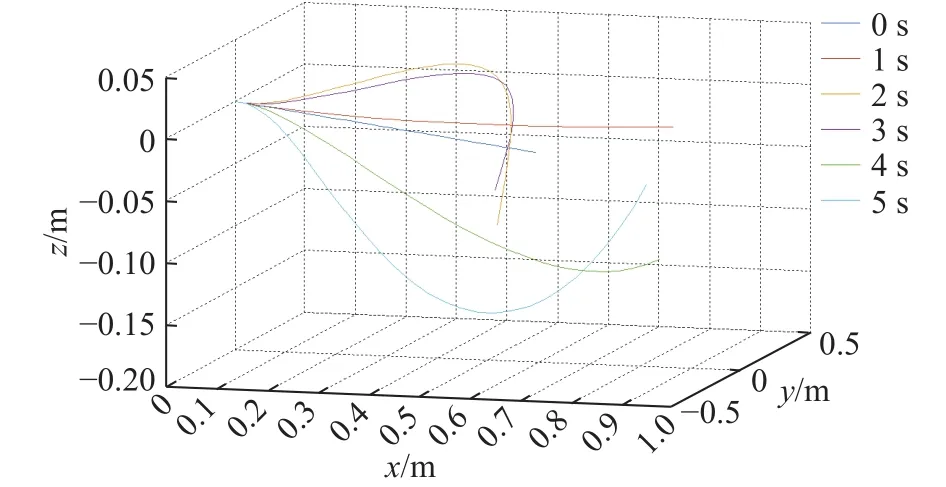
图11 软体机械臂空间运动图Fig.11 Soft manipulator spatial motion map

4 结论

本文主要介绍了一种新型的软体机械臂建模方法.该建模方法利用成熟的Cosserat梁理论，将其与软体机械臂结合起来，其次使用Ritz方法，使用一组已知的多项式的组合表示机械臂每一段的应变.这一组多项式可以被称之为“形状方程”，多项式的系数为机械臂的软体机械臂广义应变坐标.这种建模方法相比于分段恒应变的建模方法理论上可以达到更高的精度.之后针对软体臂模型中存在的未知动态，利用RBF函数设计了自适应神经网络控制器，实现了对系统未知动态的补偿，并利用李雅普诺夫稳定性分析分析了闭环系统的一致有界性，得到了系统输出可以以较小的误差跟踪给定信号的结论.接着利用BP神经网络，得到了形状空间和驱动空间的驱动力转换.仿真验证了自适应神经网络控制的有效性和系统的稳定性.

附录

为得到动力学模型中的时变系数矩阵，设计思路如下：基于Cosserat理论下，假设本文研究对象由N层堆叠而成，通过前向牛顿–欧拉运动学求解出软体臂末端速度，再借助逆运动学的形式来等效出所受应力大小，最后等效出所求动力学模型中系数矩阵的大小.具体地说，我们为求得系统中输入输出的具体映射关系：Λ=fIDM，将fIDM分成（前向运动学）A、（逆运动学）B两个流程：

流程A：前向运动学 (X(0)→X(L))，输入为

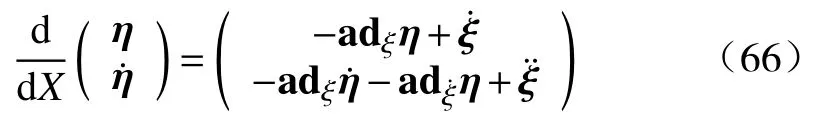
流程B：反向运动学 (X(L)→X(0))：输入为η(L),η˙(L).

为了求解等效应力大小，引入有关Cosserat杆的PDE方程模型：

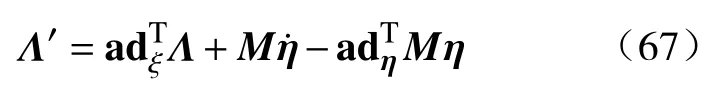
接下来，简要介绍方程（67）中各符号的物理含义与表达形式.截面惯性矩阵M=diag{ρI1,ρI2,ρI3,ρA1,ρA2,ρA3}，Mη表示沿软体臂横截面的动量.这里，ρ表示软体臂密度，I1代表扭转惯量，I2，I3代表弯曲惯量，A为横截面积.

应变场的初始状态，记为：ξ0=[ 0 0 0 1 0 0 ]T，在小应变的前提下，应力 Λ的大小与应变场 ξ之间的关系可表示为： Λ =Ht∆ξ，其中，胡克张量Ht={GI1,EI2，EI3,EA,GA,GA}，剪切模量G、 泊松比 υpoi以及杨氏模量E之间的关系为：

可将逆运动学方程组写为：

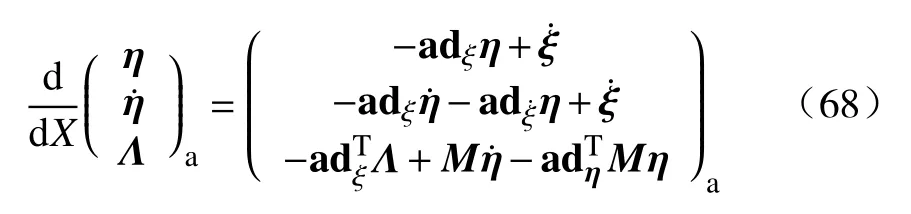
其中，（）a表示系统仅在角应变场影响下的应力变化情况，这种简化处理会极大降低计算机的仿真时间.接下来，对式（68）进行欧拉积分运算，结合拉格朗日方程（不包括非线性项），实现对驱动力的等效求解.

将上述等效过程描述为：

当映射关系fIDM()中输入仅为q，而时，从前向运动学到逆运动学后的输出，可将Qc项的大小等效出来，即：

当fIDM()输入为，时，流程B的输出为：

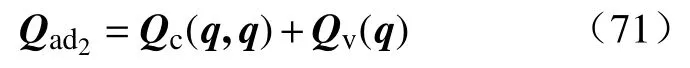
此时，可以得到有（71）式中的矩阵Qc(q,q)，Qv(q)得数值大小.为得到惯性矩阵M（q）的实际大小，需选取考虑fIDM()的输入为，其中，矩阵的值由1和0共同组成.接下来，我们将采取3次循环迭代，分别求解惯性矩阵每一列的大小值.

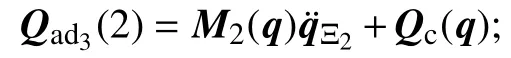
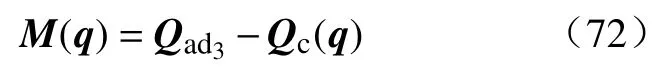
至此，可得到有关拉格朗日动力学模型（34）中所有系数矩阵的值.