Numerical Solutions of Fractional Variable Order Differential Equations via Using Shifted Legendre Polynomials

Kamal Shah,Hafsa Naz,Thabet Abdeljawad,Aziz Khan and Manar A.Alqudah

1Department of Mathematics and Sciences,Prince Sultan University,Riyadh,11586,Saudi Arabia

2Department of Mathematics,University of Malakand,Chakdara Dir(L),Khyber Pakhtunkhwa,18000,Pakistan

3Department of Medical Research,China Medical University,Taichung,40402,Taiwan

4Department of Mathematical Sciences,Faculty of Sciences,Princess Nourah bint Abdurahman University,Riyadh,11671,Saudi Arabia

ABSTRACT In this manuscript,an algorithm for the computation of numerical solutions to some variable order fractional differential equations(FDEs)subject to the boundary and initial conditions is developed.We use shifted Legendre polynomials for the required numerical algorithm to develop some operational matrices.Further,operational matrices are constructed using variable order differentiation and integration.We are finding the operational matrices of variable order differentiation and integration by omitting the discretization of data.With the help of aforesaid matrices,considered FDEs are converted to algebraic equations of Sylvester type.Finally,the algebraic equations we get are solved with the help of mathematical software like Matlab or Mathematica to compute numerical solutions.Some examples are given to check the proposed method’s accuracy and graphical representations.Exact and numerical solutions are also compared in the paper for some examples.The efficiency of the method can be enhanced further by increasing the scale level.

KEYWORDS Operational matrices;shifted legendre polynomials;FDEs;variable order

1 Introduction

Fractional calculus has been given much recognition during the last few decades.It has been got importance because of its variety of applications in mathematical modeling of real-world problems like biological and physical phenomenons [1].With the help of the aforesaid calculus,we can comprehensively explain the dynamics of various processes and phenomena in more detailed ways.Keeping these in mind,several researchers have been given attention to investigate FDEs for various results and analysis.Researchers have given much attention to studying the said area from various aspects including theoretical and numerical analysis[2].For such goals,they have developed various methods and procedures for numerical,analytical and theoretical results.These methods have been widely applied to study different problems for various results including existence,approximation and stability theory[3].

Since it is a tedious job to solve various problems of FDEs for exact or analytical solutions,therefore like classical differential equations,various tools and methods have been developed in the previous few decades to handle the said area for approximate or analytical results.In this regard,different tools and methods have been established for analytical or semi-analytical solutions like decomposition technique[4],transform method[5],perturbation method[6],etc.On the other hand several numerical procedures have been established for finding the approximate solution to various problems of FDEs.Therefore,in last two decades number of terminologies have been developed for numerical solutions to the aforesaid area.Some of the commonly used methods include Tau method[7,8],collocation method[9]and spectral method[10].The said methods have been derived by using various orthogonal and non-orthogonal polynomials like Legendre,Jacobi,Chebshev and Bernstein polynomials,etc.Spectral methods based on mentioned polynomials have been introduced for the computation of numerical solutions to various kinds of FDEs.In these methods,researchers have constructed some operational matrices of differentiation and integrations with non-integer order.To form such matrices,we need to utilize some polynomials.For instance shifted Legendre,shifted Jacobi and Bernstein polynomial have been used to construct operational matrices for the numerical solutions of various FDEs in literature(for some detail,see[11–15]).

Here,we state that in aforesaid work,authors have used collocation techniques together with spectral methods to perform numerical analysis of FDEs.Since collocation techniques need discretization of time domain of the function which is time consuming and expensive for memory.To over come this disadvantage,some authors have established operational matrices for fractional differentiation and integration by using shifted Legendre polynomial for the numerical solution of FDEs[16]by omitting the discretization and collocation.

Recently variable order FDEs have gotten some attention from researchers.Because variable order differential and integral operators have various applications in modeling different complex real-world problems.It is less well known part of calculus but has a lot of flexibility in simulating multidisciplinary processes [17].Recognizing wide applications of the said area,scientists and researchers are increasingly investigating applications of the said area to model systems of engineering and physics.Here,we remark that the first definition has been presented by Samko and Ross in 1993 (see [18]).After that,many researchers have been worked in fractional calculus by discussing the possibility of variable orders derivatives and integrations.Many research articles have been published in recent years about variable order FDEs(see[19]).

Therefore in last few years,variable order problems of integral and differential equations have gotten significant attention.This is due to the fact that these kind problems more properly describe real world phenomenon,(we refer[20]).Applications of variable order problems can also be traced in[21].Also some results about existence and existence as well as stability analysis have been published recently.Also some authors have established various scheme for numerical solutions.For more information and detail,we refer[22,23].But to the best of our information,spectral methods in this regard are very rarely used for the variable order problems.

Here we demonstrate that using spectral methods for linear problems are stable always under some specific conditions.For instance,the spectral method based on Lagendre polynomials has been proved stable for linear problem of differential equations(see[24]).Further a numerical scheme is said to be stable if it keeps the control over the numerical solution in such a way that it only depends on the degree of polynomials.For linear problems,the proposed method has been proved stable and convergent [25].Since spectral methods are converging exponentially,which demonstrate their significant accuracy than other local methods.Also spectral methods offer a suitable framework to approximate the solution of many problems.Also aforesaid methods and finite difference numerical schemes have close relation because both use same idea.The significant difference between these methods is that spectral methods utilize basis functions which are nonzero over the entire domain,while difference methods using basis functions that are nonzero only on very small sub-domains.Here we remark that as compared to finite difference methods,spectral methods are global techniques.Also numerical spectral methods use the idea of global representations to find greater order approximation.Hence these features make spectral methods more popular in recent times among the researchers(see[26]).The spectral properties of Legendre polynomials have been studied very well in literature.Here we remark some related work on properties of the said method as[27–30].

Motivated from the above discussion and work,we extend our scheme based on shifted Legendre polynomials for some variable order problems under initial and boundary conditions.We investigate two classes of variable order initial and boundary value problem as

and

wheregis linear continuous function from [0,1])→Rand 1＜ α1(t)≤ 2,0＜ α2(t)≤ 1.We establish operational matrices on the basis of shifted Legendre polynomials for our considered problems.Keeping in mind that we avoid descritization and collocation to form some operational matrices of variable order integration and differentiation.Based on these matrices,proposed problems are converted to some algebraic type matrix equations of Sylvester type.Then upon using Matlab,we solve the Sylvester equation to get the required numerical solution.The advantage of our proposed method is that it saves time and extra memory.Further,we testify several examples and present their solutions of variable order at different points graphically.

Our paper is structured as:Section 1 is devoted to introduction.Section 2 is related to basic results and derivation of operational matrices.Section 3 is related to general algorithm.Section 4 is related to numerical examples.Last section is devoted to brief conclusion and discussion.

2 Preliminaries

In this section,we recall definitions of variable order integration and differentiation which can be read in[19,23,31,32].

Definition 2.1.The variable order integration of a functionh∈L[0,1]withα(t)＞0 is defined as

whereα(t)is a continuous and bounded function.

Definition 2.2.Letα(t)＞0 is a continuous and bounded function andh∈C[0,1],then the Caputo differential operator for variable order is defined as

For more properties of variable order differentiations and integrations,we refer[21,22].

Definition 2.3.[11]The recursive relation for shifted Legendre polynomials over the interval[-1,1]is defined as

First two polynomials are given asL0=1,L1(t)=t.

Next we recall orthogonality condition from[11,16]which are needed in our approximation.

Definition 2.4.The orthogonality condition is defined as

Using the orthogonality condition given in Eq.(6),any functionhcan be approximated in terms of aforementioned polynomial as

The above Eq.(7)can also be written in vector form as

Lemma 2.1.Convergence analysis:Ifh∈CN+1[0,1],then the best approximation ofhgiven in Eq.(8)over[0,1]is defined by

In same line ifh∈S,such thatSdenotes the spanning set of firstNLegendre polynomials.Then,we takeh(t)≈and

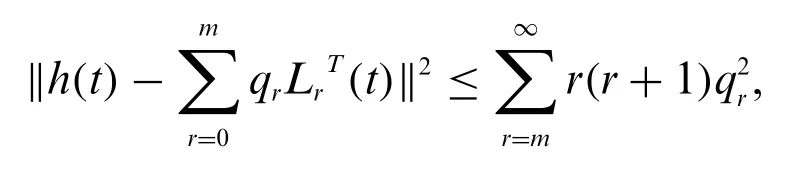
whereqr=(2r+1)(t)dt.

Proof.The proof is same as given in[33].

Operational matrices corresponding to variable order integration and differentiation are established by following the procedure given in[11,16].

Lemma 2.2.Ifbe the vector function of Legendre polynomials,then the variable order integration is defined as

where

whereb=0,1,2,....

Corollary 1.With the help of operational matrix given in Eq.(10),the error

is bounded.The concerned error bound is computed as

where the constantsdkare denoting the spectral coefficients of

Lemma 2.3.Let(t)be the vector function,then fractional variable order differentiation of(t)is given bywhereis operational matrix of variable orderα(t)differentiation given by

where

withb=0,1,2,....

Corollary 2.The error in computation of variable order differentiation of a functionUis given by

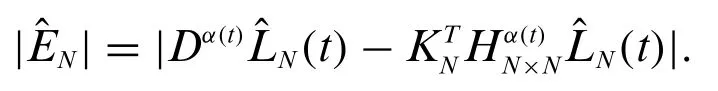
Further the said error is bounded by

Lemma 2.4.LetΘ(t)be defined over the interval[0,1]andV(t)=then

where

Proof.The proof is same as done in[16].

3 General Algorithms for Variable Orders Problems

Here,we establish the required scheme for initial and boundary value problems of variable order FDEs in two sub-sections.

3.1 Construction of Algorithm for Variable Initial Value Problem

Consider the following case,whenα(t)∈(0,1]as

Consider

By the application of fractional variable integration with orderα(t),Eq.(14)implies that

By using initial condition,one hasa0=Insert value ofa0in Eq.(15)yields

We write the approximation asandg(t)=After simplification,Eq.(13)gives

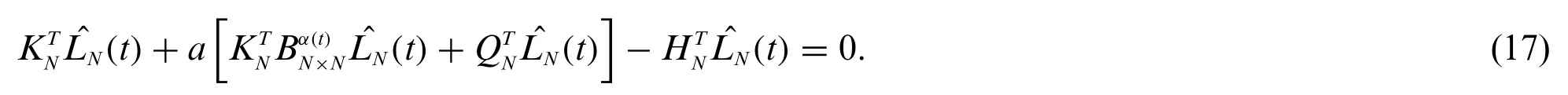
Further simplification implies that

This is a simple Sylvester type algebraic equation.Upon using Matlab,we solve it to compute the coefficient matrixto receive the required numerical solution of(13).

3.2 Algorithm for Variable Order Boundary Value Problem

Here,we construct the general scheme for variable order problems,when 1＜α2(t)≤2,0＜α1(t)≤1 as

Assume that

By applying the fractional order integration of orderα2(t),Eq.(21)implies that

Eq.(22)can be written as

By using the initial and boundary conditions,we can easily getc1=and forc2useU(1)=in Eq.(23)to get

By inserting the values of constantsc1,c2in Eq.(23),we have

On using Lemma 2.4 and after simplification Eq.(25),one has

where

Now by the use of Lemma 2.4,one has

Insert Eqs.(21),(25)and(27)in(20),one has

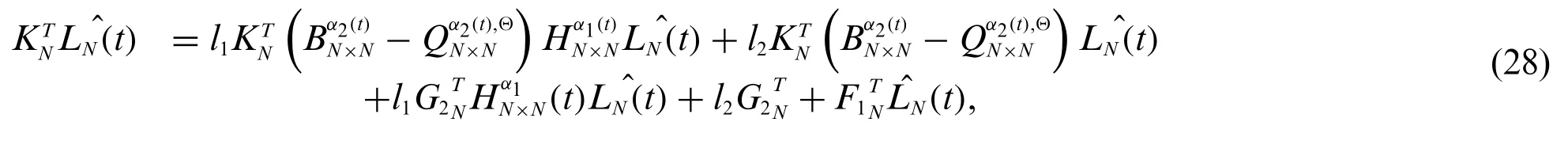
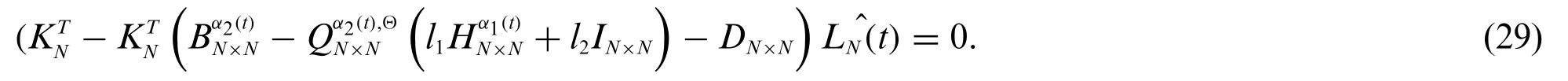
After simplification,we get

Eq.(30) is simple algebraic equation of Sylvester type and can be solved through the Matlab software for required numerical solution.

4 Illustrative Examples

Here we give examples for both kinds of problems in two sub-sections.

4.1 Numerical Examples for Variable Initial Value Problems

Consider the following example as

Example 1.

Forα(t)=e-t,the exact solution is given by

where

Here,we give graphical presentation of approximate solution for different values of variable order attand the corresponding absolute error using scale level equal to 5 in Figs.1 and 2,respectively.

Figure 1:Graphical presentation of approximate solutions and absolute error of Example 1

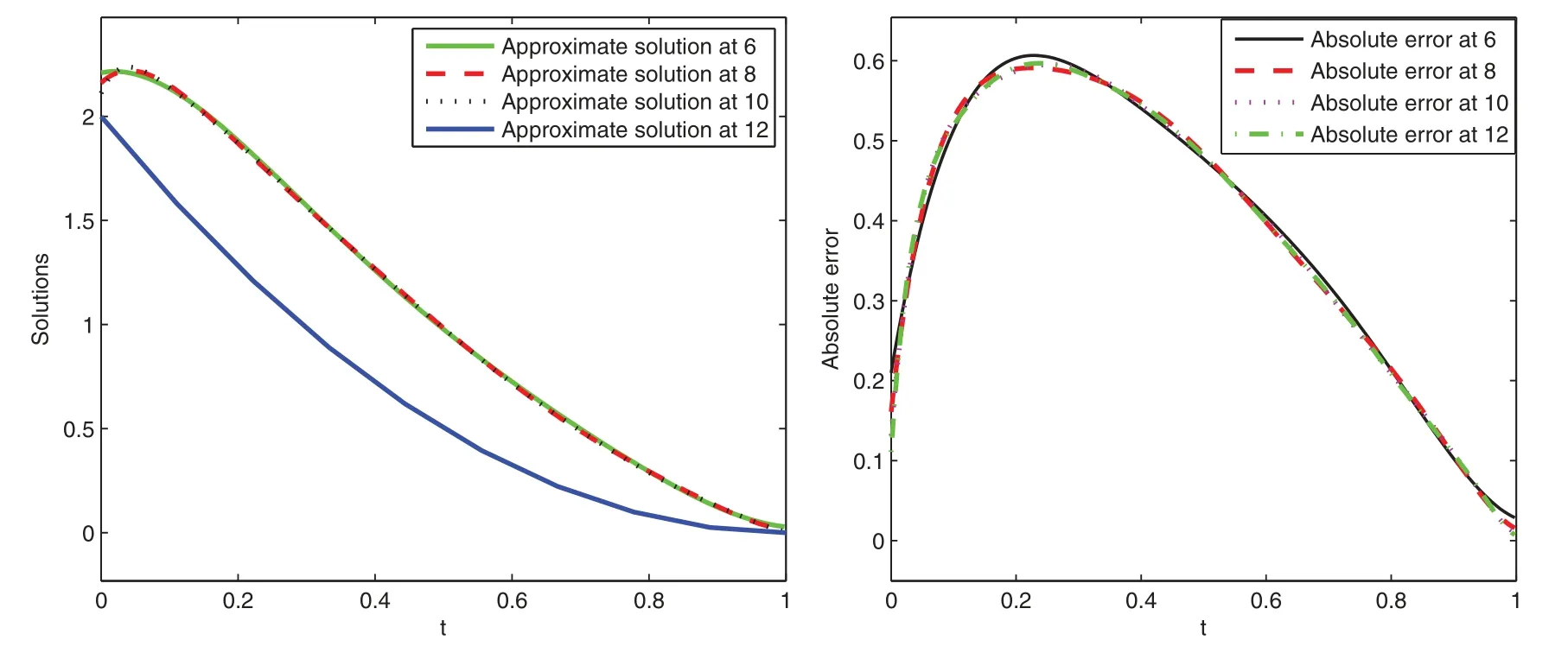
Figure 2:Graphical presentation of approximate solutions and absolute error of Example 1 at various scale level and at t =0.75

Example 2.Consider another problem as

U(t)=t2+t+1,

where the source functiongis given as

Here,we give graphical presentation of approximate solution for various values of variable order attand the corresponding absolute error using scale level equal to 6 in Figs.3 and 4,respectively.

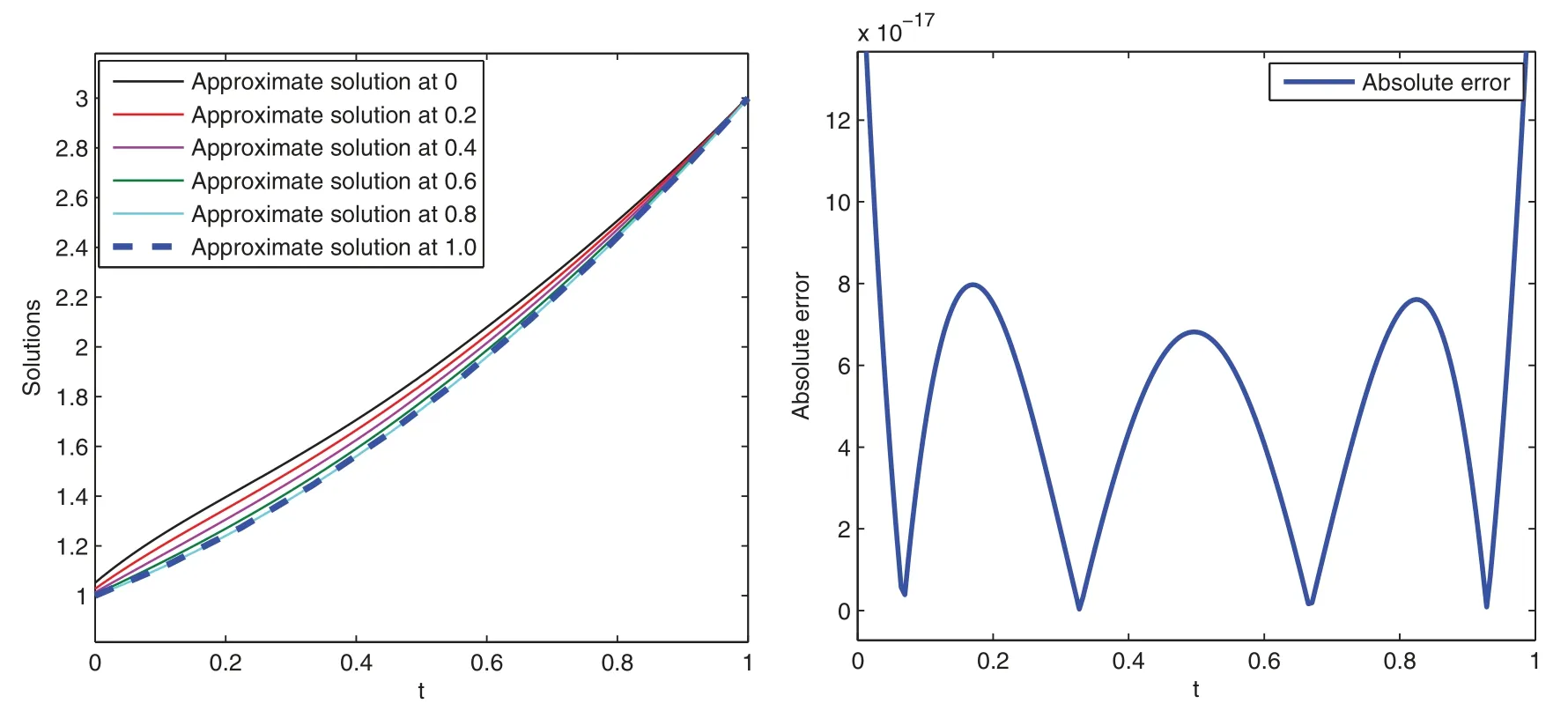
Figure 3:Graphical presentation of approximate solutions and absolute error of Example 2

Figure 4:Graphical presentation of approximate solutions and absolute error of Example 2 at various scale level and at t =0.75

4.2 Numerical Examples for Variable Order Boundary Value Problems

To demonstrate the second scheme for boundary value problems,we give some examples here.

Example 3.Consider the problem

Forα(t)=sin(t)+1,the exact solution is given byU(t)=t4.Further,the source function is given as

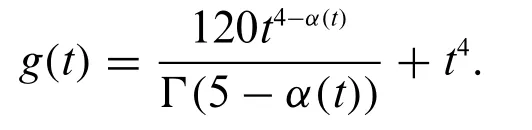
Here,we give graphical presentation of approximate solution for various values of variable order attand the corresponding absolute error using scale level equal to 6 in Figs.5 and 6,respectively.

Figure 5:Graphical presentation of approximate solutions and absolute error of Example 3 at various values of t and scale level 6

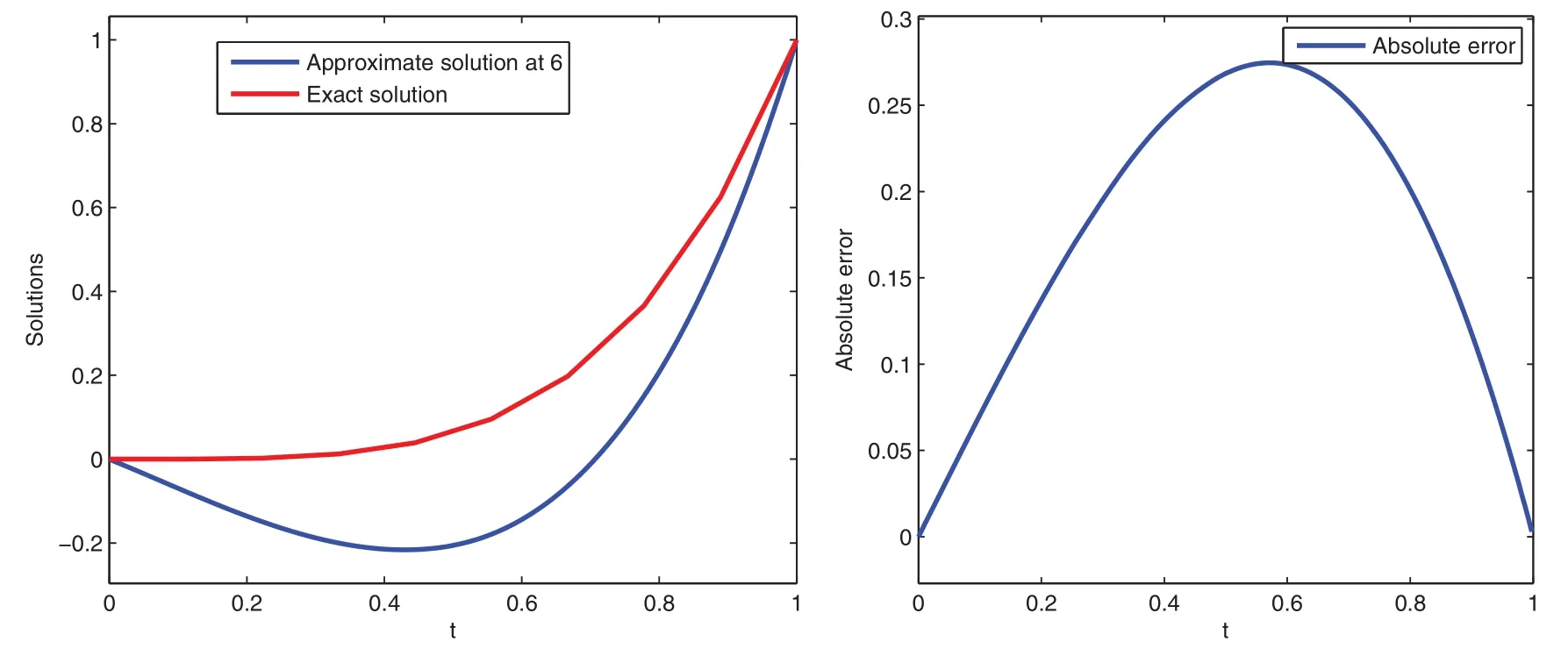
Figure 6:Graphical presentation of approximate solutions and absolute error of Example 3

Example 4.Consider the problem as

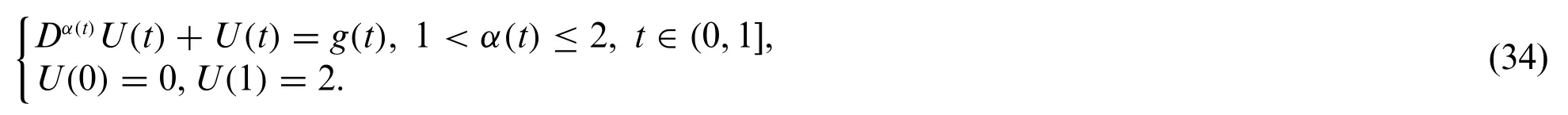
Here,we give graphical presentation of approximate solution for various values of variable order attand the corresponding absolute error using scale level equal to 6 in Figs.7 and 8,respectively.

Figure 7:Graphical presentation of approximate solutions and absolute error of Example 4 at various values of t and scale level 6

Figure 8:Graphical presentation of approximate solutions and absolute error of Example 4

5 Conclusion and Discussion

In this research paper,various classes of variable order FDEs have been studied under boundary and initial conditions for numerical solutions.Properties of shifted Legendre polynomials have been used to develop operational matrices for fractional variable order derivative and integration.Based on these operational matrices,considered problems with initial/boundary conditions have been reduced to algebraic equations of the Sylvester type.By using mathematical softwares like Matlab,we have solved the obtained algebraic equation for the required numerical solution.In this regard,various examples have been solved based on the proposed method.We have omitted the collocations and sub-division of the time domain in small intervals.Also,the proposed spectral method has been proved stable.Moreover,some error analysis has been recorded which shows that the greater the scale level higher be the accuracy and vice versa.From our numerical experiments,we have observed that the accuracy of the proposed method is excellent and can be improved further by enlarging the scale level.Because of using a higher scale level,the efficiency of the proposed method can be improved very well.An absolute error has also been computed at different scale levels.We have also examined various problems using different fractional variable order to check the results.Hence,from numerical examples,we have concluded that the operational matrices method based on shifted Legendre polynomials can also be used as a powerful tool to handle different classes of variable order FDEs as well as integral equations for their numerical solutions.

Data Availability:The data used has been included within the paper.

Acknowledgement:This paper has been read and approved by all authors.Also authors Kamal Shah,Aziz Khan and Thabet Abdeljawad would like to thank Prince Sultan University for support through research lab TAS.

Funding Statement:Princess Nourah bint Abdurahman University Researchers Supporting Project No.(PNURSP2022R14),Princess Nourah bint Abdurahman University,Riyadh,Saudi Arabia.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.