Stability Scrutinization of Agrawal Axisymmetric Flow of Nanofluid through a Permeable Moving Disk Due to Renewable Solar Radiation with Smoluchowski Temperature and Maxwell Velocity Slip Boundary Conditions

Umair Khan,Aurang Zaib,Anuar Ishak,Iskandar Waini,El-Sayed M.Sherif and Dumitru Baleanu

1Department of Mathematical Sciences,Faculty of Science and Technology,Universiti Kebangsaan Malaysia,Bangi,43600,Malaysia

2Department of Mathematics and Social Sciences,Sukkur IBA University,Sukkur,65200,Pakistan

3Department of Mathematical Sciences,Federal Urdu University of Arts,Science&Technology,Karachi,75300,Pakistan

4Fakulti Teknologi Kejuruteraan Mekanikal dan Pembuatan,Universiti Teknikal Malaysia Melaka,Melaka,76100,Malaysia

5Mechanical Engineering Department,College of Engineering,King Saud University,Riyadh,11423,Saudi Arabia

6Department of Mathematics,Cankaya University,Ankara,06790,Turkey

7Institute of Space Sciences,Magurele,077125,Romania

8Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,40447,Taiwan

ABSTRACT The utilization of solar energy is essential to all living things since the beginning of time.In addition to being a constant source of energy,solar energy(SE)can also be used to generate heat and electricity.Recent technology enables to convert the solar energy into electricity by using thermal solar heat.Solar energy is perhaps the most easily accessible and plentiful source of sustainable energy.Copper-based nanofluid has been considered as a method to improve solar collector performance by absorbing incoming solar energy directly.The goal of this research is to explore theoretically the Agrawal axisymmetric flow induced by Cu-water nanofluid over a moving permeable disk caused by solar energy.Moreover,the impacts of Maxwell velocity and Smoluchowski temperature slip are incorporated to discuss the fine points of nanofluid flow and characteristics of heat transfer.The primary partial differential equations are transformed to similarity equations by employing similarity variables and then utilizing bvp4c to resolve the set of equations numerically.The current numerical approach can produce double solutions by providing suitable initial guesses.In addition,the results revealed that the impact of solar collector efficiency enhances significantly due to nanoparticle volume fraction.The suction parameter delays the boundary layer separation.Moreover,stability analysis is performed and is found that the upper solution is stable and physically trustworthy while the lower one is unstable.

KEYWORDS Agrawal axisymmetric flow;solar energy;nanofluid;heat transfer;slip conditions

1 Introduction

Energy is critical to the advancement of human civilization or society(HS).Though,over the last century,the rapid advancement of HS has led to worldwide energy crises and severe environmental pollution.To find a way to sustainable development,all countries need to take advantage of new energy sources and develop new energy technologies.The sun is perhaps most likely the greatest clean source of heat in the form of energy accessible these days.Renewable sources of energy involve solar energy(which comes from the sun and can be converted into heat and electricity),hydropower from water,biomass from plants,geothermal energy (from within the earth),and wind energy.Solar energy,a renewable and environmentally approachable energy source,has been producing energy for thousands of years.Nanomaterials are new energy materials because their particle size is equal to or less than the wavelength of the coherent wave and the de Broglie wave.As a result,nanoparticles dissipate incident radiation both strongly and independently.The use of nanofluids in solar thermal systems has emerged as a new research focus predicated on the properties of radiative motion of nanoparticles.According to Angstrom[1]and Keshavarz et al.[2],SE is one of the best sources of renewable energy with the least amount of environmental impact.In the 1970s,Hunt [3] gave a basic idea of utilizing particles to capture solar energy.The situation has been demonstrated that merging nanomaterials in a liquid(nanofluid)has a significant impact on the liquid’s thermophysical characteristics,like thermal conductivity.Lu et al.[4] utilized nanofluids in solar collectors through vacated tubes.Kandasamy et al.[5]utilized the Hiemenz time-dependent flow of Cu-water nanoparticles over a permeable wedge due to SE with thermal stratification and applied Lie group analysis to find the numerical solution.Anbuchezhian et al.[6] scrutinized the magneto liquid flow with heat transfer via a nanoparticle over a vertical porous stretchable sheet owing to solar radiation.They detected that the profiles of temperature enrich due to radiation impact.The time-dependent (TD) magneto flow conveying by nanofluid past a permeable wedge in a non-Darcy porous medium was inspected by Kandasamy et al.[7].They observed that the copper nanoparticles played an important role and absorb solar radiation incidents.Makinde et al.[8] discussed the impacts of Joule heating and chemical reaction on the magneto flow in a nanofluid through a heated stretchable sheet induced in a porous medium with solar radiation.The surface concentration and temperature gradients are found to be increasing functions of the non-Darcy parameter.Talebi et al.[9]experimentally inspected the forced convection flow and heat transfer induced by hybrid nanofluids with the fixed condition of heat flux in the laminar regime.Acharya[10]quantified the pattern of the flow and the behavior of heat transfer containing hybrid nanofluid induced by erratic solar radiation for different thermal apparatus of solar.Asadikia et al.[11,12] prepared high-performance nanofluids using the electrical and thermal conductivities of carbon nanotubes and copper oxide nanoparticles to improve the properties of heat transfer.According to the experimental data,the thermal conductivity increases proportionally to the number of nanoparticles but decreases in alkaline environments.Sarkar et al.[13]evaluated the features of fluid flow of time-dependent nanoliquid towards a stagnation point through a spinning sphere owing to Hall current and solar radiation.Asadikia et al.[14]experimentally scrutinized the water and ethylene glycol-based Fe2O3/SWCNT hybrid nanofluid by using genetic algorithms and neural networks.The entropy analysis of fluid flow within a slant permeable cavity induced by hybrid nanofluid with heat generation was examined by Chamkha et al.[15].They observed that the dispersion of nanoparticles reduces thermal performance for several Rayleigh numbers.Recently,Shoeibi et al.[16]evaluated the performance of a solar still by employing hybrid nanofluids cooling of the glass.The temperature difference between condensation and evaporation areas is increased by hybrid nanofluid protection cooling.

The slip boundary condition is defined as the module of tangential speed at the body surface that is proportional to the wall gradients (shear stress).After establishing a link between slip rate and shear stress,Navier [17] coined the term slip boundary condition.Maxwell [18] gave the most basic enlightenment for the momentum slip,which is based on a momentum gradient accommodation exerting normal to the surface as well as the creep term.Later,Smoluchowski[19]goes on to illuminate the concept of slip temperature.Ramya et al.[20] inspected the impacts of momentum and thermal slips on the dynamics of fluid flow scattered in nanomaterials.The rates of heat and mass transfer are reduced as the thermal slip parameter is increased.Khashi et al.[21]elaborated the impressions of slip and CBCs on a 3D flow comprising two dissimilar kinds of nanomaterials over a stretching/shrinking surface.The stability analysis has been performed to validate the stable solution.Jünemann et al.[22]utilized the Smoluchowski temperature boundary as well as Maxwell slip condition to stimulate the behavior of operation of screw machines.Recently,Sajid et al.[23]developed a 3D model subject to Sutterby rotating fluid flow in an expandable slippery surface with Smoluchowski temperature and Maxwell slip conditions.They discovered that in the case of a constant reaction rate,the thermal radiation parameter improves the heat transfer by 17.2 percent and the mass transfer by 62.1 percent.

A rigid or stiff body moving via a fluid(i.e.,automobile,sports ball,missile,space travel vehicle),or in the recovery of oil in the industry (the extraction of crude oil from a lubricant ground is accomplished through gas equivalently or injection),a stagnation point signifies as an exterior flow encroaches in a stationary-point on the exterior of a submerged body within a flow,where the speed of the object is zero at the surface of the submerged object.Hiemenz[24]was the first to precisely analyze the classic problem of 2D stagnation-point flows(SPFs).As a result,the flow guided perpendicular to a flat infinite plate has an exact solution.The axisymmetric flow(AF)near a stagnation point(SP)from a plate was investigated by Homann[25].Ramya et al.[20]and Howarth[26]extended the 2D flow and axisymmetric flow to the 3D flow case using the approximation of the boundary layer in the path normal to the plane surface.In addition,Davey[27]developed an innovative axisymmetric SPF and presented an analytic solution to the Navier–Stokes equations by using spherical coordinates.On the contrary to the Agrawal [28] outer irrotational flow,this flow is rotational in the far-field.Weidman[29]has prolonged Agrawal’s work toward the situation of SP rotational flow impingement on a stretchable radially surface.Weidman [30,31] analyzed the AGAF near a SP from a respective stretched and flat sheet.Recently,Ro¸sca et al.[32] investigated the viscous fluid flow impinging towards a stretching/shrinking sheet in a nanofluid and presented double solutions.

The axisymmetric flow past a permeable moving continuous disk in the existence of Maxwell and Smoluchowski slip conditions after being inspired by the literature mentioned aboveis simulated in this paper.In the existence of radiative solar energy,the thermal impartiality of the entire model is developed.The copper nanoparticles are used to simulate a flow with water as the base medium.There are very few publications dealing with axisymmetric flow induced by nanofluid flow past a stretching/shrinking sheet influenced by solar radiation.As a result,our novel exploration into the influence of radiative solar energy as well as slips interactions will help engineers implement nanofluids positively and effectively.The multiple solutions of the considered model are also one of the main interests of this work for the phenomena of shrinking and stretching disk.Therefore,stability analysis is also implemented to check which result is physically realizable.

2 Mathematical Modeling of the Problem

Consider the characteristics of heat transfer analysis and steady Agrawal axisymmetric SPF of a copper water-based nanofluid through a porous moving disk in the presence of solar energy radiation as shown schematically in Fig.1.The flow configuration of the model is articulated in the form of cylindrical coordinates(ra,θa,za)measured in the radial,azimuthal and axial directions respectively,along with accompanying velocity modules(ua,va,wa).The AGF is exclusively symmetric to theraθa-plane and likewise axisymmetric to the coordinateza-axis,i.e.,the change with respect to the coordinateθais completely ignored.The surface is positioned atza= 0,and the upper half-plane is the essential domain of the fluid flow.Further presume that the variable far field or ambient velocity is emphasized viaue(ra,za)=2brazaandwe(ra,za)=-2,wherebcorresponds the arbitrary factor evaluating the magnitude of the AGF having dimensions(LT)-1,see Weidman[31].In addition,the wall variable velocity is highlighted viauw=b2/3υ1/3f raalong with the requisite posited Maxwell slip velocity[12]having slip lengthhave been employed to examine the momentum slip effect while the transparent constant mass flux is equal towA,wherewA ＜0 is for the case of suction andwA ＞0 is for the case of blowing.The Smoluchowski temperature slip [19] and the wall constant temperature is designated viaandT,respectively,while the free-streamwconstant temperature is denoted viaT∞by means of the phenomenonTw ＞T∞.The surroundings and the Newtonian absorber are both kept at a constant temperatureT∞,far away from the moving disk surface.Furthermore,an incoming radiation flux of intensityqris received by the non-reflective,absorbent,preferably transparent movable disk.Rendering to Fathalah et al.[33],thisqrpenetrates the moving disk surface and is absorbed in a neighboring fluid with an absorption coefficient.Heat is transported from the disk surface to the surroundings as the absorbing nanoliquid and the moving disk surface are heated by SE.Also,solar radiation is a collimated beam that is perpendicular to the surface of the disk.As stated before,the regular(viscous)fluid is supposed to have heat absorption properties.However,the thermophysical properties of the working fluid and the nanoparticle are taken to be constant.Due to the significant impression of the aforesaid assumptions of the problem,the leading constitutive equations in terms of PDEs can be simply and written as Eqs.(1)–(4)(see Weidman[31]):

along with subject to the boundary conditions in Eq.(5)

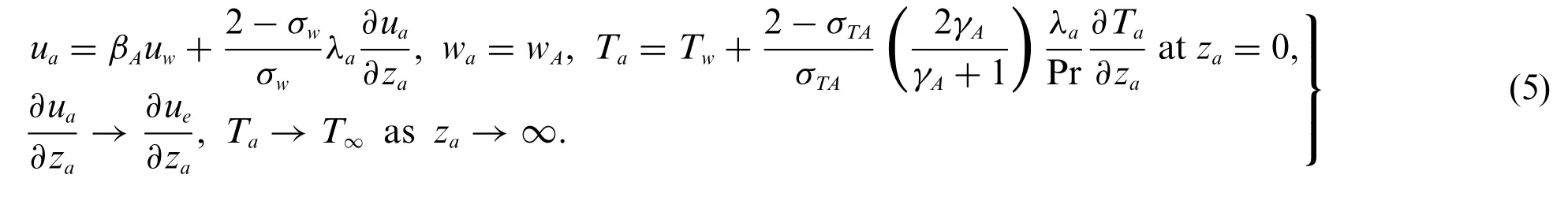
Here,waanduaare the velocity components alongzaandraaxes,σwcorresponds the coefficient of tangential momentum accommodation,Pais the pressure,σTAcorresponds the coefficient of thermal accommodation,λacorresponds the main free path coefficient,Tacorresponds the temperature,γAcorresponds the specific heat ratio coefficient andβAcorresponds the dimensionless shrinking/stretching constraint withβA ＜0 for shrinking,βA ＞0 for stretching,andβA=0 for the motionless disk.

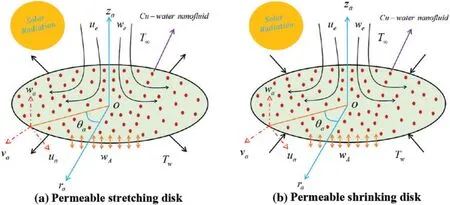
Figure 1:Physical model of the Agrawal flow problem

In addition,the thermo-physical expressions of the copper-water based nanofluid are set by[34]in Eq.(6):

whereφnamely resembles to the nanoparticles volume fraction which is equal to the mixtures of copper nanoparticle(Cu)and the regular(viscous)fluid(H2O).Additionally,kf,ρf,μfandindicate the thermal conductivity,density,dynamic viscosity,and the specific heat capacity at a constant pressure of the regular (viscous) fluid,respectively,whileks,ρsandare the respective quantities of the solid nanoparticles.Moreover,the subscriptssandfare classified as the solid nanoparticles and the base fluid,respectively.The experimental thermophysical characteristics of the regular pure liquid(water)and copper(Cu)nanoparticles are depicted in Table 1.

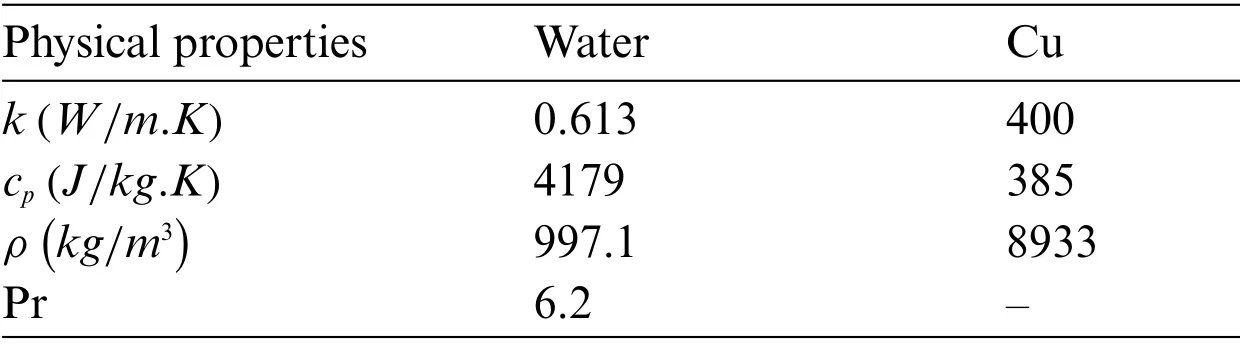
Table 1: The thermophysical properties of Cu/water nanoparticles

Furthermore,the last term on the right-hand side of Eq.(4)is incorporated specially to demarcate the radiative heat fluxqr.Also,given an optically thick fluid (nanofluid) layer,one can express the simplified version of theqrusing the Rosseland approximation can be as Eq.(7)(see Hayat et al.[35]):

whereσaandkasignify the Stefan Boltzmann and the mean absorption constants.Using Taylor series approximation centered around the pointT∞,the termcan be simplified asby neglecting the second and higher order power terms.

For making the system of equations dimensionless,the following similarity variables are employed in Eq.(8)(see Weidman[31]):

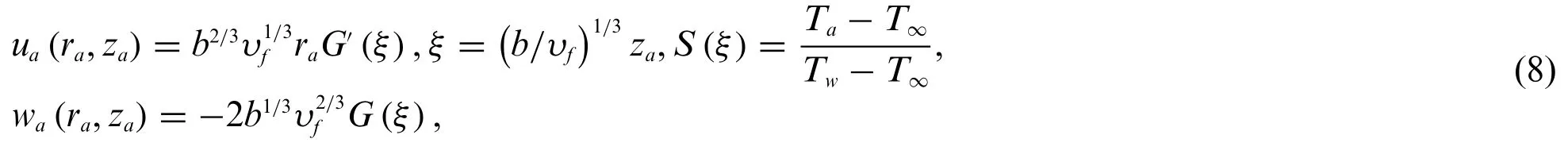
where primes denote the differentiation w.r.tξand the last term of Eq.(8)leads to yield:

Here,fw=G(0)divulges the transparent mass flux dimensionless constraint withfw ＞0 andfw ＜0 resemble to blowing and suction,respectively,whilefw= 0 indicates the surface of the impermeable disk.

Now the similarity transformations are plugged into Eqs.(2) to (4),where Eq.(1) is identically satisfied and the rest of the equations are transformed to the following similarity ODEs:

with boundary conditions:

The dimensionless parameters in the aforesaid equations include the velocity slip parameterδA=the Prandtl number Pr =υf/αf,the thermal slip factorδB=and the radiation parameterNr=

The quantities of engineering practical importance are the friction factorCf rain the radial direction and the Nusselt numberNura,which are given as:

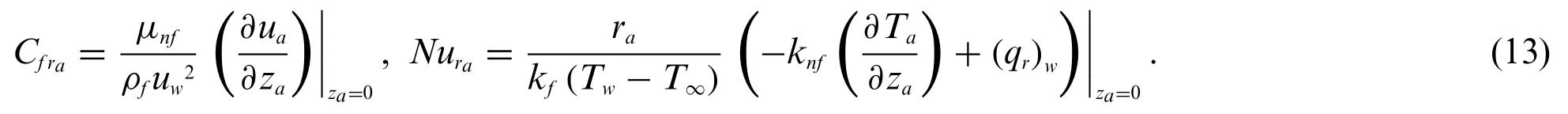
Using similarity transformations in the above Eq.(13),we get Eq.(14):

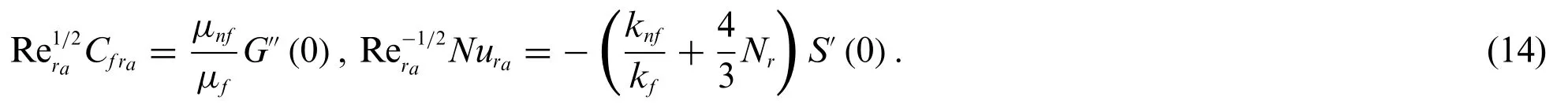
where Rera=corresponds to the local Reynolds number.

3 Temporal Stability Analysis

In this segment,we study the stability of the multiple(upper and lower)solutions as time evolves.Merkin[36]was the first researcher to introduce the analysis of this technique,later;it was followed by Weidman et al.[37].For the measured working procedure,initially,we start from the new variables as follows:

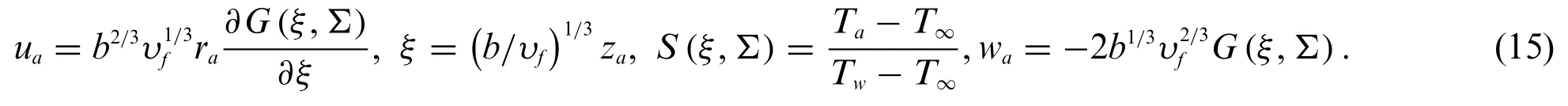
whereΣ=symbolizes the new dimensionless time.Further,executing the above Eq.(15)into the time-dependent or unsteady form of the requisite governing Eqs.(2)to(4),which can take place the form as:

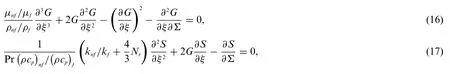
subject to the appropriate BCs:

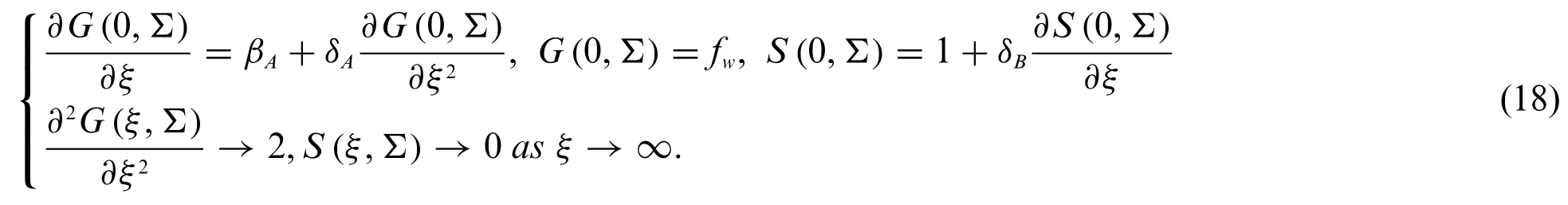
According to Weidman et al.[37],the time-independent outcomeG=G0andS=S0of the similarity Eqs.(10)to(12)are perturbed as follows:

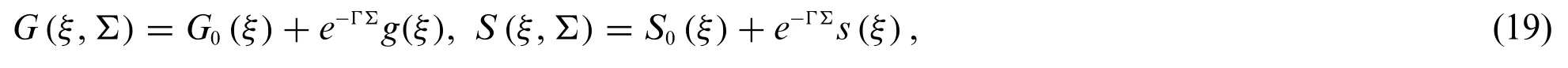
where the functionsg(ξ)ands(ξ)in Eq.(19)are relatively small compared toG0(ξ)andS0(ξ).The stability of the outcomes is determined by the sign(positive or negative)of the eigenvalueΓ.Therefore,exercising Eq.(19)into the above Eqs.(16)and(17)which can take place the form as:

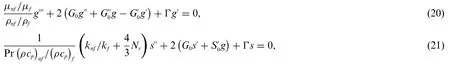
along with BCs:

The corresponding positive or negative values ofΓin the above Eqs.(20)and(21)are found by setting the value ofg′(0)ors′(0).Without loss of generality,we setg′(0)= 2 and solve the set of coupled Eqs.(20)to(22)to find the eigenvaluesΓ.

4 Numerical Technique

The set of similarity Eqs.(10)and(11)with appropriate BCs(12)were cracked computationally by employing the bvp4c package available in MATLAB.The working procedure of the considered bvp4c scheme is described in detail by Shampine et al.[38]as well as Khan et al.[39].The recognized bvp4c approach was also built on a well-known finite difference approach that used the Lobatto IIIA collocation formula to construct a C1-continuous result.The syntax of the bvp4c solver is demarcated by “Sol = bvp4c (@OdeBVP,@OdeBC,Solinit,Options)”.Moreover,to start working on the employed technique,the system of second and third order equations is changed to the required first order by introducing the latest notations and rewriting them as follows:

Now to utilize the aforementioned Eq.(23)in the dimensionless set of Eqs.(10)–(12)to derive the set of first-order ODEs,which has the form:

To treat the above set of differential equations as an initial boundary value problem,the following unknown and known initial conditions are considered:

Moreover,the above-mentioned constantsB1andB2are guessed during the bvp4c numerical execution by utilizing an operational shooting algorithm as explained practically by Khan et al.[39],in such a way that the executed iterative process is repeated multiply until satisfying all the following boundary conditions at once:

Two alternative initial guesses for the values of the skin friction coefficient and the heat transfer rate are used to investigate the double (upper and lower) solutions.To get the preferred outcomes,the suitable starting estimate and thickness of the boundary layerξ∞must be selected based on the parameters implemented.To authenticate the considered numerical scheme,the values ofG′(0)are compared with the case that has been reported in Weidman [30] for regular (viscous) fluid (φ= 0)with several values ofβAwhenfw=0 andδA=0 as presented in Table 2,which displays a satisfactory agreement.From this comparison,it can be noticed that the existing results for upper and lower branch solutions are usable and consistent.Therefore,we can conclude that the generated algorithm for the numerically investigating Agrawal(Cu-water)nanofluid flow can be used with great confident.

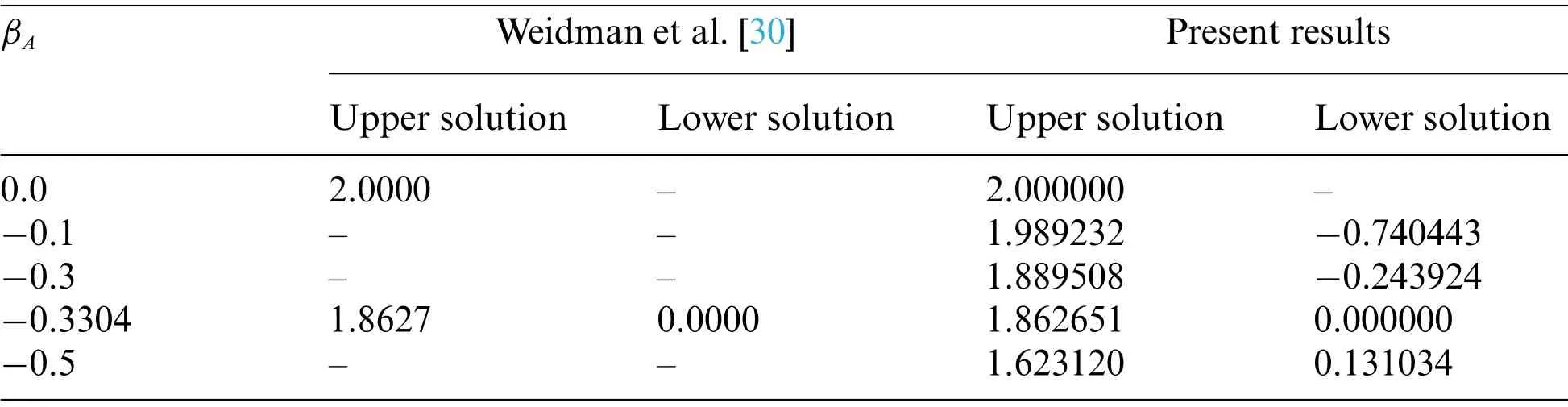
Table 2:A comparison of the G′(0)with Weidman et al.[30]for different values of βA when φ =fw =0 and δA =0

Table 2 (continued)

5 Analysis of Results and Discussion

The present work aims to investigate the influence of the distinguished parameters such as the moving disk parameterβA,the velocity slip parameterδA,the thermal slip parameterδB,the radiation parameterNr,the mass suction parameterfw,and the nanoparticles volume fractionφon the reduced heat transfer,temperature profile and reduced shear stress of the(Cu-water)nanofluid for the double results as revealed in Figs.2 to 9.Moreover,the computational values of the reduced shear stress and heat transfer of the(Cu-water)nanofluid for the upper branch solution(UBS)and lower branch solution (LBS) with the influence of the several influential parameters whenλ= -1.5 (shrinking sheet)and Pr=6.2 are elucidated in Tables 3 and 4,respectively.The numerical and graphical behavior of the eigenvaluesΓfor several values ofβAis presented in Table 5 and Fig.10,respectively.For the aims of computation,the fix values of the embedded distinguished factors are written as follows:βA= -1.4,fw= 0.5,δA= 0.05,δB= 0.5,Nr= 1.5 andφ= 0.03.Therefore,the UBS and LBS throughout the graphs are signified by the black solid and dash lines,respectively,while the small solid red,blue,and grey balls are called the bifurcation point.The stable solutions are found on the UB,while unstable solutions are found on the LB.The stable solutions are of physical interest because they may be tested experimentally or understood practically.

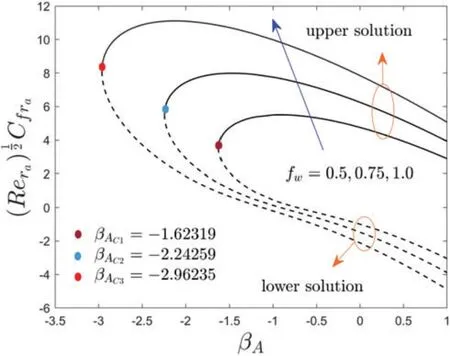
Figure 2:Variations of ReCf ra against βA for dissimilar choices of fw

Figure 3:Deviations of ReNura against βA for several values of fw

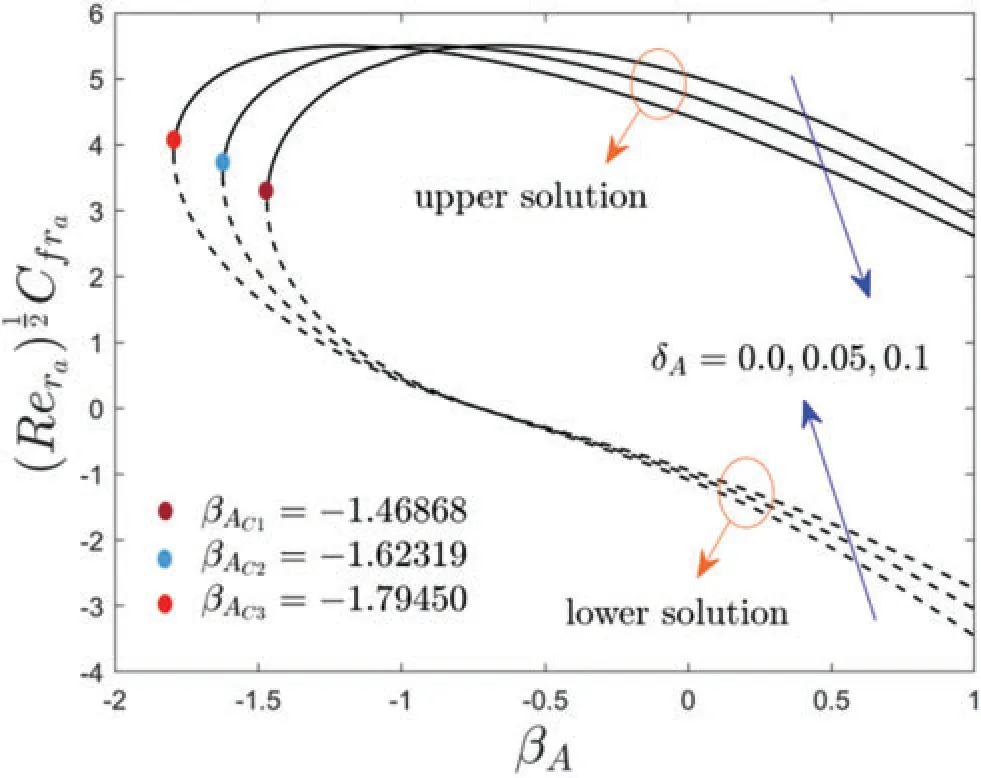
Figure 4:Variations of ReCf ra against βA for dissimilar choices of δA

Table 3 displays the numerical values of the shear stress for the UB and LB outcomes with the influence ofφ,fwandδAwhenβA= -1.5.From the table,it can be seen that the wall drag force upsurges for UB but decreases for the LB with higher values offwandδAwhile it is improved in two dissimilar branch results for developed impressions ofφ.In addition,the wall drag force is higher for the stable result and lesser for the unstable outcome withfwas compared to the consequence of the factorsδAandφ.Alternatively,the numerical values of the heat transfer for the UB and LB results with the impact ofφ,fw,δA,NrandδBwhenβA= -1.5 and Pr = 6.2 as highlighted in Table 4.The heat transport phenomenon elevates for UB as well as for LB with the higher impact offw,Nrandφwhile it is shrinkages for UB and LB due toδB.Also,the impressions ofδAcan boost up the tendency of thermal transport for the stable result but decline for the unstable solution.

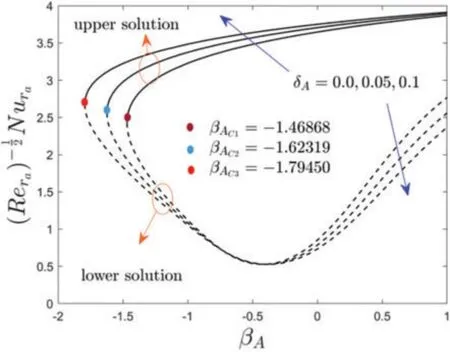
Figure 5:Variations of ReNura against βA for several values of δA

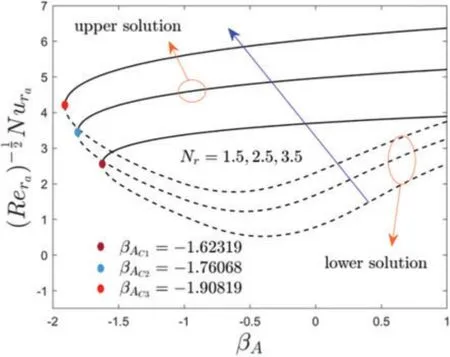
Figure 6:Variations of ReNura against βA for dissimilar choices of Nr

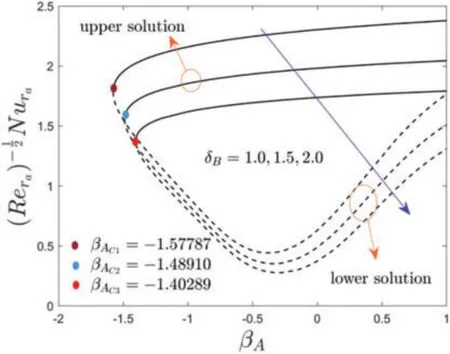
Figure 7:Deviations of ReNura against βA for several values of δB

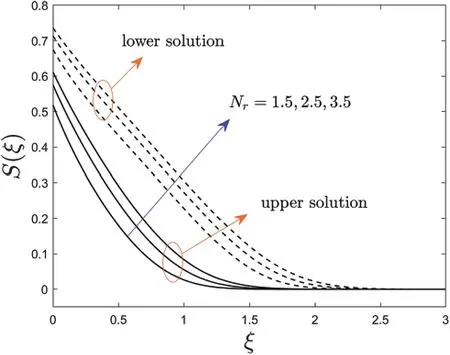
Figure 8:Variations of S(ξ)against ξ for several values of Nr

Figure 9:Variations of S(ξ)against ξ for several values of δB

Table 3:Values of the wall drag force for the numerous distinct selected values of the parameters when βA =-1.5(shrinking sheet)

Table 3 (continued)

Table 4:Values of-S′(0)for the numerous values of the selected parameters when βA =-1.5(shrinking sheet)and Pr=6.2

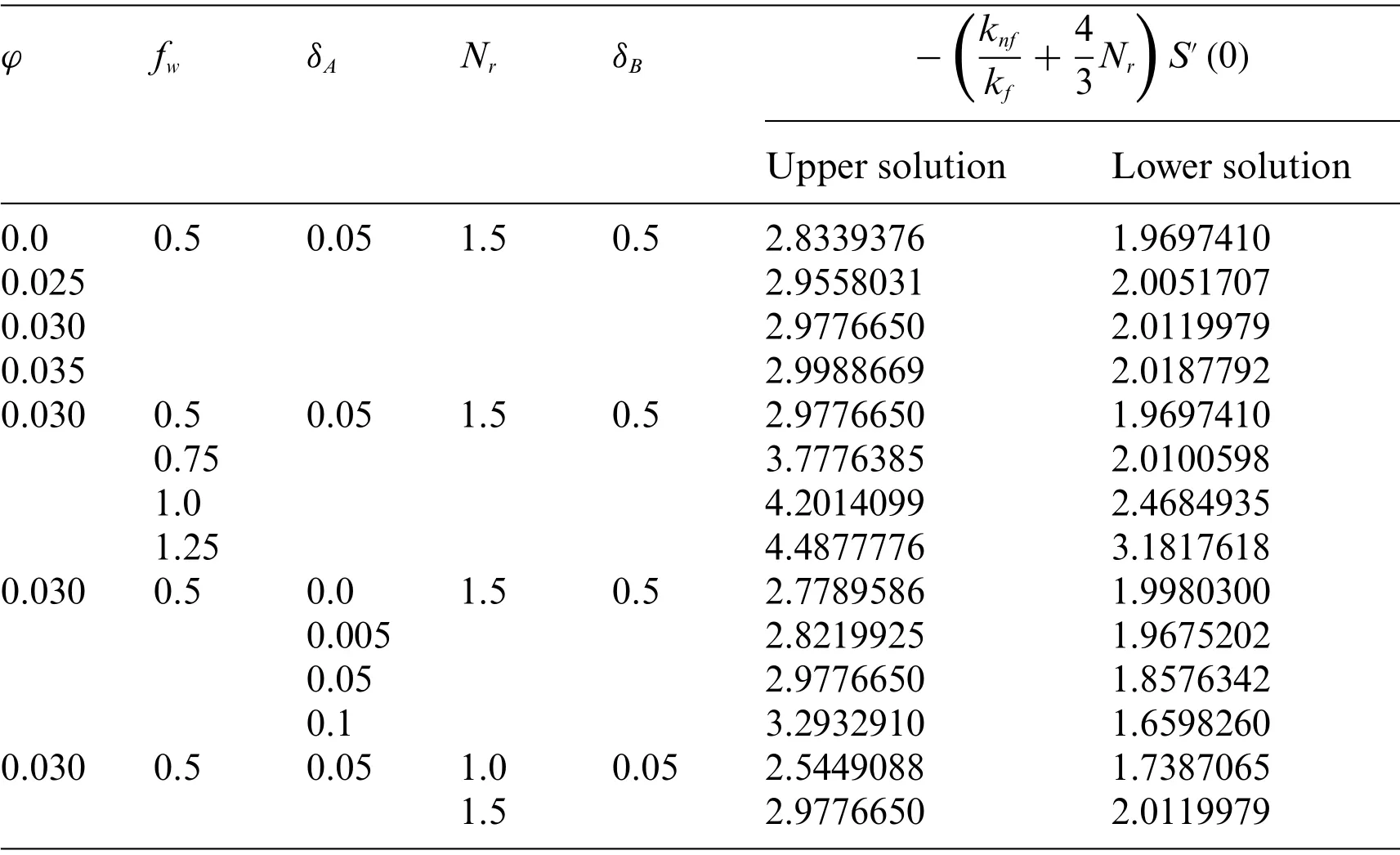
Table 4:Values of-S′(0)for the numerous values of the selected parameters when βA =-1.5(shrinking sheet)and Pr=6.2

(Continued)

φ fw δA Nr δB -knf kf+ 43Nr S′(0)Upper solution Lower solution 0.0 0.5 0.05 1.5 0.5 2.8339376 1.9697410 0.025 2.9558031 2.0051707 0.030 2.9776650 2.0119979 0.035 2.9988669 2.0187792 0.030 0.5 0.05 1.5 0.5 2.9776650 1.9697410 0.75 3.7776385 2.0100598 1.0 4.2014099 2.4684935 1.25 4.4877776 3.1817618 0.030 0.5 0.0 1.5 0.5 2.7789586 1.9980300 0.005 2.8219925 1.9675202 0.05 2.9776650 1.8576342 0.1 3.2932910 1.6598260 0.030 0.5 0.05 1.0 0.05 2.5449088 1.7387065 1.5 2.9776650 2.0119979

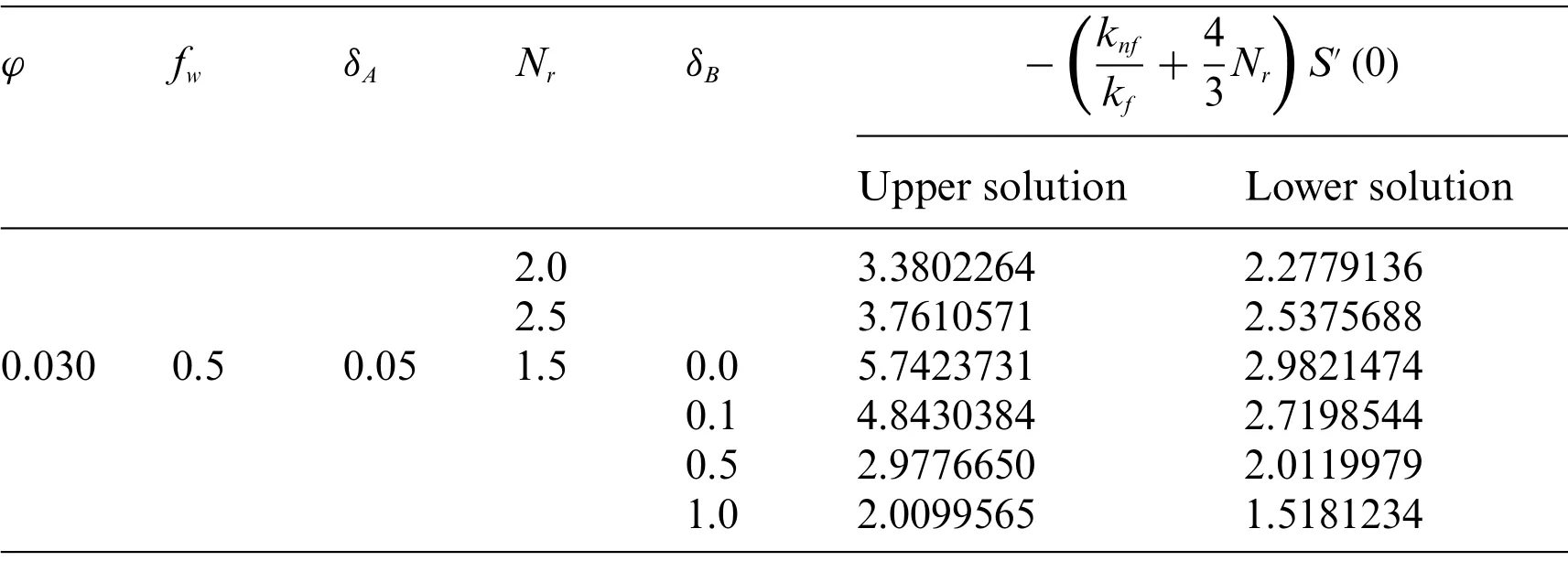
Table 4 (continued)

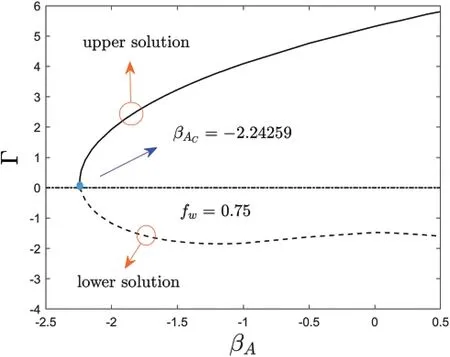
Figure 10:Eigenvalues of Γ for several values of βA

Figs.2 to 7 elucidate the variation of wall drag force,and heat transferof the copper water-based nanofluid againstβAdue to the influence offw,δA,NrandδB,respectively.From these figures,it can be seen that two distinct branch solutions exist for the Eqs.(10)to(12)in the range ofβA ＞βACfor both moving disk parameter or stretching/shrinking parameter,a unique solution found whenβA=βACand no solution is obtained whenβA ＜βAC,whereas,βACcorresponds the bifurcation value ofβAwhich the upper and lower solution merge.

Moreover,Figs.2 and 3 show the inspirations offwon the wall friction force and heat transfer of the(Cu-water)nanofluid againstβA.From the responses,it is observed that the upswing offwaugments the wall drag force for the UBS but declines for the LBS while-S′(0)is expressively widened with both(UB and LB)solutions.The existence of the solution domain for the occurrence of multiple(UB and LB)solutions is also increasing with the developed impressions offw.Physically,an increase infwcauses a flow of nanoparticles towards the moving disk surface,as a result,lowering the velocity,and hence the wall drag coefficient is developing.Therefore,the gap between the UB curves is relatively more as compared to the curves of the LB(see Figs.2 and 3).For growing values offwthe magnitude of bifurcation values(BVs)get developed.Therefore,the following BVs are found such as-1.62319,-2.24259,and -2.96235 for the respective selected values offw.This trend recommends that growing values offwdecelerates the separation of boundary layers.

In Figs.4 and 5,the variations of the multiple (UB and LB) solutions with the change of the velocity slip parameterδAare demonstrated with the wall drag force and heat transfer of the copper water-based nanoparticles,respectively.For growing values ofδA,the wall drag force decreases and increases for the UBS in the specific range ofβAwhile it is followed the contrary patterns for the LBS as compared to UBS for higherδA.Physically,the liquid particles and the motion of the disk are different at the surface of the moving disk in the corresponding Maxwell slip BCs phenomena,which devalues the motion of fluid and specially the outcomes drop in the velocity fields.As a result,the friction factor in the radial path upsurges near the bifurcation point.In contrast,the heat transfer enriches for upper branch solution with larger values ofδAwhile the impacts ofδAis reversed for the lower solution curves.Moreover,the wall drag force behavior of the solution changes twice (for the UBS as well as for the LBS)at some finite valueβ0ofβAdue to the larger value ofδAwhile for heat transfer it is changed the only single time for the LBS curves.Owing to the improvement of the velocity slip parameterδA,the bifurcation values of the moving disk parameter are-1.46868,-1.62319,and-1.79450,respectively.In this respect,the separation of the boundary layer becomes suspended with the superior value ofδA.

The influence of the radiation parameterNrand temperature slip parameterδBon the heat transfer againstβAis revealed in Figs.6 and 7,respectively.From the outcomes,it is perceived that the rate of heat transfer elevates for both solution branches withNrbut decelerates due to the larger value ofδB.Generally,the liquid particles attract more thermal heat by increasing the radiation parameter;as a response,the heat transfer increases(see Fig.6).In addition,with the selected change value ofNr,the subsequent BVs are found such as-1.62319,-1.76068,and-1.90819,respectively.To see more deeply,the pattern of the BVs decreases withNran d consequently,the separation of boundary layer shrinkages.Alternatively,the magnitude of the BVsreduces for the larger value ofδBas presented in Fig.7.Therefore,the behavior of the solution curves specifies that the boundary layer separation augments withδB.

Figs.8 and 9 describe the behavior of the typical temperature profiles for the multiple solutions of the copper-water base nanoparticles against the pseudo-similarity variableξwithNrandδB,respectively.The temperature profile in Fig.8 augments for both branches of solution with a rise inNr.The physical reason is thatNris the key factor of the improvement of heat transfer.This situation is divulged that the-S′(0)enlarges via the asset of augmentation in the value ofNr.It is since an upsurge inNrshrinkages thekawhich consequently drives to appreciation in temperature profiles.Conversely,the typical temperature decelerates for multiple(upper and lower)solutions due to the enhancement in the value ofδB(see Fig.9).The general reason is that the increment inδBlessening the distance between the wall moving surface of the disk and the free-stream temperature which convey less energy or heat to the liquid particles from the moving disk surface,and subsequently lessen the fluid temperature and the temperature profile as well.

Finally,Table 5 displays the eigenvaluesΓagainstβAfor the UB and LB solutions,while the rest of the comprised constraints are taken to be fixed.The data shown in the table are further plotted in the form of a graph(see Fig.10)which can distinguish the behavior of the upper and lower solution noticeably.This graph is drawn for the positive and negative values ofΓagainstβA.So,for the obtained smallest positive numerical values ofΓ,it is distinguished thate-ΓΣ→0 as time evolves(Σ→∞).In the meantime,for the negative numerical values ofΓ,it is observed thate-ΓΣ→0 as time evolves(Σ→∞).Therefore,the UBS is stable and hence physically trustworthy asΣ→∞,while the LBS is not.

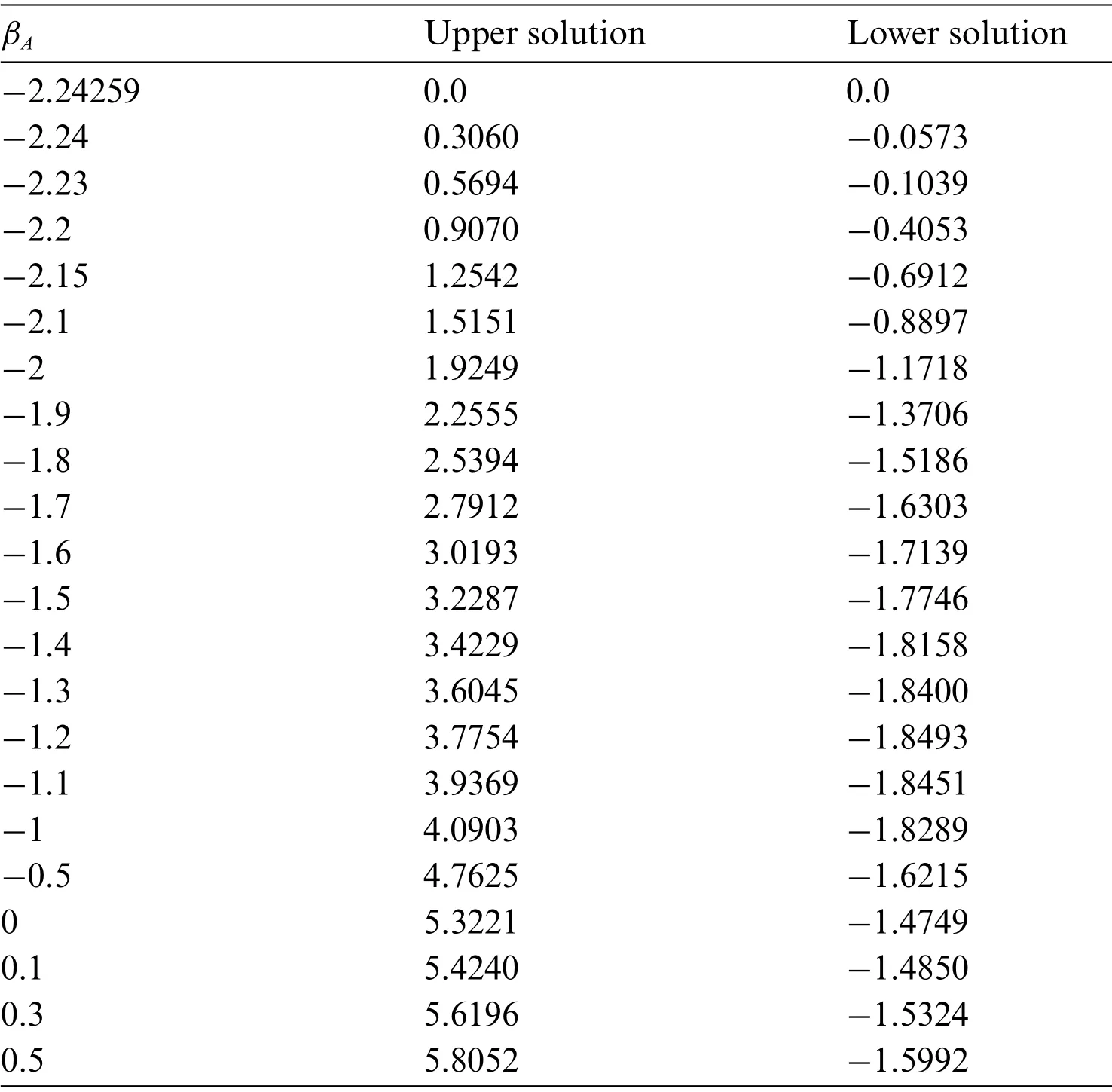
Table 5: The numerical eigenvalues of Γ for several values of βA

6 Conclusions

The influence of Maxwell velocity and Smoluchowski temperature slip conditions on the Agrawal steady axisymmetric SPF of (Cu-water) nanofluid via a moving continuous disk comprising the significant impacts of suction/injection owing to solar energy radiation has been examined.The employment of a similarity transformation for the steady Agrawal nanofluid flow is of particular relevance in this work.The significant outcomes are summarized as follows:

· The shear stress and heat transfer have been found to show double(UB and LB)solutions over a wide range of moving disk parameter or stretching/shrinking parameter.

· The shear stress uplifts due tofwin the UB solution and shrinks in the case of LB solution;however,the heat transfer augments due tofwin both cases.

· The heat transfer for the upper and lower solution branches enhances due toNr,while it shrinkages with a higher value ofδB.

· The thermal boundary layer thickness of (Cu-water) nanofluid is decayed for both branches owing to the development ofδB,while it is strengthened due to the larger value ofNr.

· The domain of existence of multiple(upper and lower)solutions significantly improves for the larger values of the temperature slip parameter,radiation parameter,velocity slip parameter,and suction parameter.

· The velocity slip parameterδBhas a dramatic impact on the shear stress for the UB and LB solutions while the heat transfer rate is increased and decreased significantly with a higher value ofδBfor the UB and LB solutions,respectively.

· The magnitude of the bifurcation or critical values enhances due to enlarging values ofNr,fwandδB,but reduces with the superior value ofδB.

· The boundary layer separation is delayed or broken down with a higher impact ofNr,fwandδBwhile the separation of the boundary layer is escalated owing to a higher value ofδB.

· Well-disposed to the analysis of stability,it was established that the UB solution is physically stable and trustworthy,while the LB solution is not.

The influence of nanoparticles on the absorption of radiative energy has been of interest for many years in a variety of applications.Nowadays,researchers are interested in the radiation properties of nanoparticles in liquid suspensions,especially for medical and other engineering or technical applications.In addition to the advantages of optical and radiative properties,nanofluids provide other advantages such as improved thermal conductivity and particle stability over micrometer-sized suspensions and the operation of direct-absorbing solar collectors.Nanofluids have been shown to possess improved heat transport properties and higher energy efficiency in a variety of thermal exchange systems for different industrial applications,such as transportation,electronic cooling,military,nuclear energy,aerospace,etc.Nanofluids powered by solar energy are important because they can be used in many heat transfers and other applications such as detergents,solar panels,drying processes,heat exchangers,geothermal and oil recovery,and building construction,etc.

7 Future Work

The future potential investigations of interest are as follows:

· The current work can be extended by considering the hybrid nanofluids to investigate the Agrawal flow.

· The time-dependent flow may be considered in future work.

· The mixed convection flow may be considered.

Acknowledgement:This research was supported by Researchers Supporting Project No.(RSP-2021/33),King Saud University,Riyadh,Saudi Arabia.

Funding Statement:The authors received the financial support from King Saud University,Riyadh,Saudi Arabia through Project No.RSP-2021/33.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.