2022年高考“概率与统计”试题分析及复习建议

张 琥(正高级教师 特级教师)

(北京外国语大学附属苏州湾外国语学校)

1 考试内容分析

概率与统计是中学数学课程中的主要内容之一,«普通高中数学课程标准(2017年版2020年修订)»对这部分内容的设置较«普通高中数学课程标准(实验)»有所增加.2022年高考全国卷中概率与统计试题重在对基础知识的考查,突出对数学思想方法、统计与概率的基本原理的理解和应用.2022年高考全国卷中考查概率与统计的主要内容如表1所示.

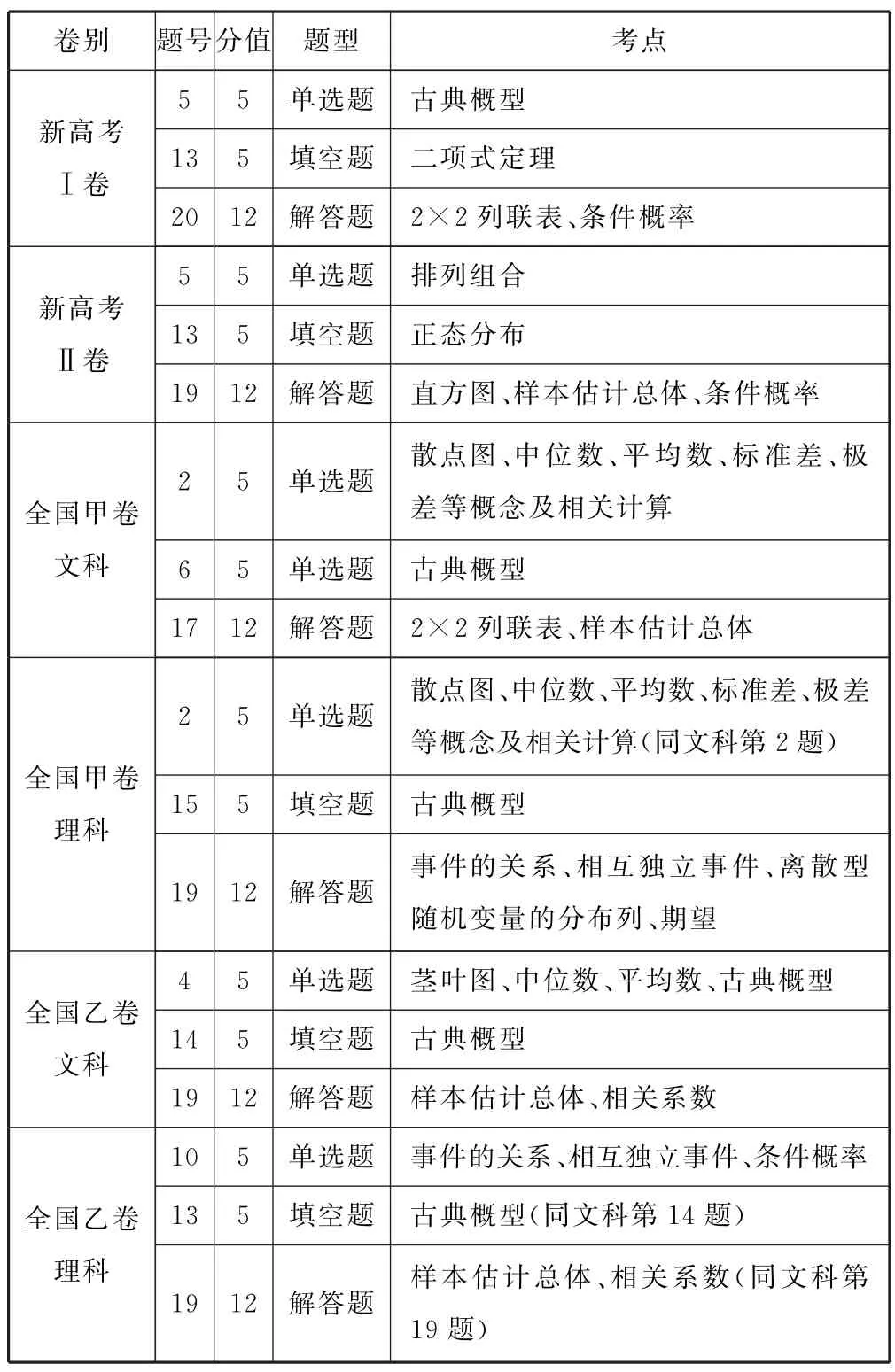
表1

从表1可以看出,在6份全国卷中,对统计与概率知识的考查,题型均是2 道小题和1 道大题,共3道题,所占分值均是22分.新高考Ⅱ卷考查了条件概率,其他5份试卷均考查的是古典概型;新高考Ⅱ卷、全国(甲、乙)卷文科、全国乙卷理科均考查了用样本的数字特征估计总体的数字特征.

2 试题特点分析

6份全国卷中的概率与统计题特点鲜明,涉及知识点有排列组合、二项式定理、古典概型、样本平均数、样本方差、线性回归、正态分布、独立性检验等.在以统计知识为背景下考查概率问题,还常常在与函数知识的交会处命题,命题背景多与生产生活联系,体现一定的综合性和应用性.

2.1 知识考查重理解

例1 (2022年全国甲卷理15)从正方体的8个顶点中任选4 个,则这4 个点在同一个平面的概率为________.

2.2 方法考查重积累

例2(2022年新高考Ⅱ卷19)在某地区进行流行病学调查,随机调查了100 位某种疾病患者的年龄,得到如下的样本数据的频率分布直方图(如图1).

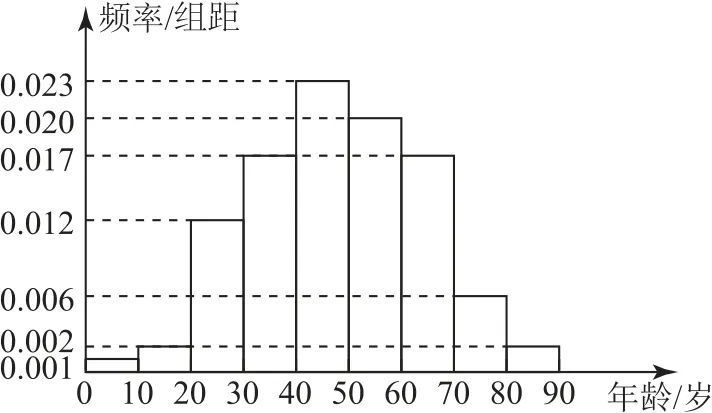
图1

(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);

(2)估计该地区一位这种疾病患者的年龄位于区间[20,70)的概率;

(3)已知该地区这种疾病的患病率为0.1%,该地区年龄位于区间[40,50)的人口占该地区总人口的16%.从该地区中任选一人,若此人的年龄位于区间[40,50),求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).

(2)由频率稳定于概率的原理,用样本的频率作为概率的估计值,设A＝{一人患这种疾病的年龄在区间[20,70)},根据对立事件的概率公式P(A)＝1－P(ˉA),可求出年龄位于区间[20,70)的概率为0.89.

(3)根据条件概率公式即可求出此人患这种疾病的概率约为0.0014.

2.3 技能考查重熟练

例3(2022年北京卷18)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m).

甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;

乙:9.78,9.56,9.51,9.36,9.32,9.23;

丙:9.85,9.65,9.20,9.16.

假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.

(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;

(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望E(X);

(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大? (结论不要求证明)

(2)求解出X的分布列,从而可计算出X的数学期望为

(3)计算出甲、乙、丙得最高成绩的概率,再根据其最高成绩可判断出丙获得冠军的概率估计值最大.

3 解题分析

例4(2022年新高考Ⅰ卷5)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为( ).

例5(2022年全国甲卷文6)从分别写有1,2,3,4,5,6的6张卡片中无放回地随机抽取2张,则抽到的2 张卡片上的数字之积是4 的倍数的概率为( ).

例6(2022年新高考Ⅱ卷5)有甲、乙、丙、丁、戊5 名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同排列方式共有( ).

A.12种 B.24种 C.36种 D.48种

例7(2022年全国乙卷文14、理13)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为________.

例9(2022年北京卷8)若(2x－1)4＝a4x4＋a3x3＋a2x2＋a1x＋a0,则a0＋a2＋a4＝( ).

A.40 B.41 C.－40 D.－41

例10(2022年全国甲卷文、理2)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10 位社区居民在讲座前和讲座后问卷答题的正确率如图2 所示,则( ).

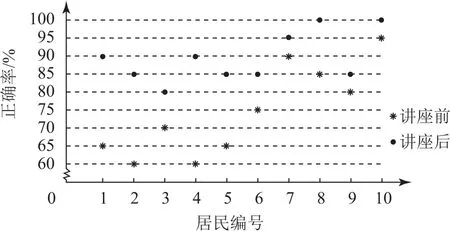
图2

A.讲座前问卷答题的正确率的中位数小于70%

B.讲座后问卷答题的正确率的平均数大于85%

C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差

D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差

例11(2022年全国乙卷文4)分别统计了甲、乙两位同学16 周的各周课外体育运动时长(单位:h),得到如图3所示的茎叶图,则下列结论中错误的是( ).

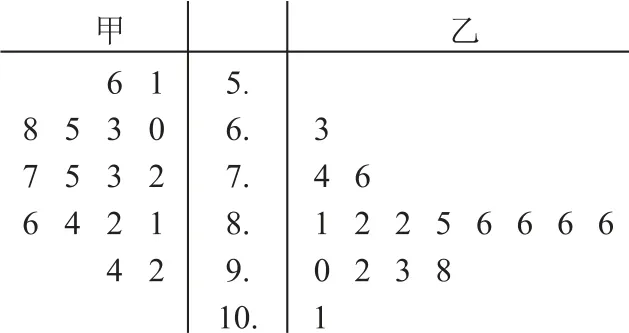
图3

A.甲同学周课外体育运动时长的样本中位数为7.4

B.乙同学周课外体育运动时长的样本平均数大于8

C.甲同学周课外体育运动时长大于8的概率的估计值大于0.4

D.乙同学周课外体育运动时长大于8的概率的估计值大于0.6

综上,选C.

例12(2022年新高考Ⅱ卷13)已知随机变量X服从正态分布N(2,σ2),且P(2＜X≤2.5)＝0.36,则P(X＞2.5)＝________.

例13(2022年新高考Ⅰ卷20)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如表2所示的数据.

表2

(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?

(2)从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良好”,B表示事件“选到的人患有该疾病的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.

(ⅱ)利用该调查数据,给出P(A|B),P(A|ˉB)的估计值,并利用(ⅰ)的结果给出R的估计值.

表3

又P(K2≥6.635)＝0.01,24＞6.635,所以有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异.

(2)(ⅰ)因为

例14(2022 年全国乙卷理10)某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3,且p3＞p2＞p1＞0.记该棋手连胜两盘的概率为p,则( ).

A.p与该棋手和甲、乙、丙的比赛次序无关

B.该棋手在第二盘与甲比赛,p最大

C.该棋手在第二盘与乙比赛,p最大

D.该棋手在第二盘与丙比赛,p最大

记该棋手在第二盘与乙比赛,且连胜两盘的概率为p乙,则

记该棋手在第二盘与丙比赛,且连胜两盘的概率为p丙,则

即p甲＜p乙,p乙＜p丙,则该棋手在第二盘与丙比赛,p最大,所以D 正确,B 和C 错误.p与该棋手与甲、乙、丙的比赛次序有关,所以A 错误.

综上,选D.

例15(2022年全国乙卷文、理19)某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如表4所示的数据.

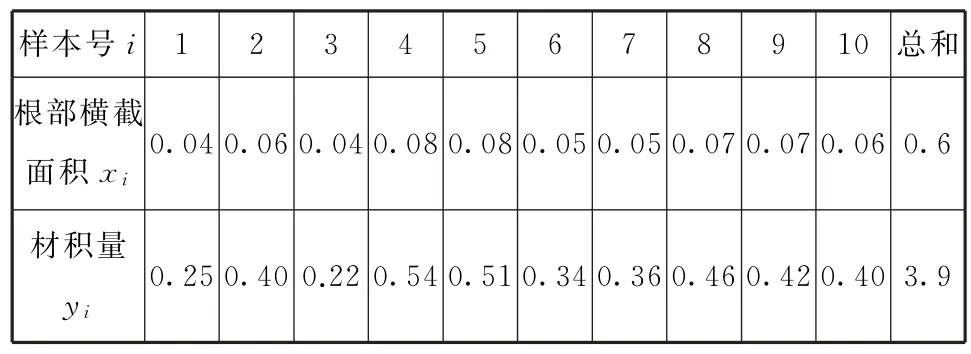
表4

(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;

(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);

(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186m2.已知树木的材积量与其根部横截面积近似成正比,利用以上数据给出该林区这种树木的总材积量的估计值.

(3)设该林区这种树木的总材积量的估计值为Ym3,又已知树木的材积量与其根部横截面积近似成正比,可得解得Y＝1209 m3,则该林区这种树木总材积量估计为1209m3.

例16(2022年全国甲卷文17)甲、乙两城之间长途客车均由A和B两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到列联表如表5所示.

表5

(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;

(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?

表6

(2)列联表如表7所示.

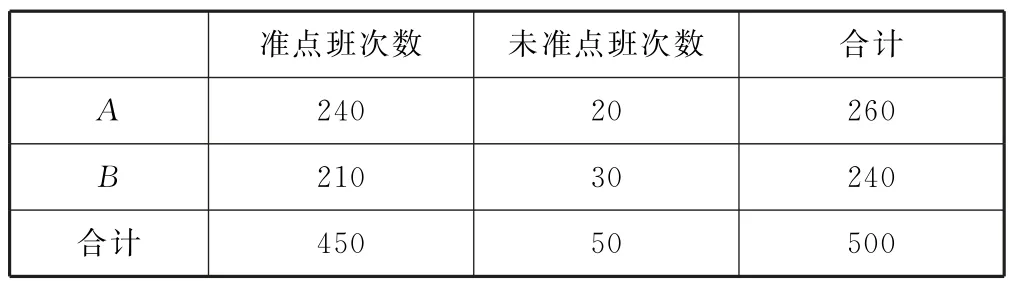
表7

根据临界值表可知,有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.

例17(2022年全国甲卷理19)甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.

(1)求甲学校获得冠军的概率;

(2)用X表示乙学校的总得分,求X的分布列与期望.

(2)依题可知,X的可能取值为0,10,20,30,所以

即X的分布列如表8所示.

表8

4 命题趋势

通过对近年全国高考卷,特别是近三年新高考卷的分析与研究,我们预计2023年高考对概率与统计的考查将继续秉持新高考卷的命题风格,强调对基本概念和基本公式的理解、应用,突出对运算求解能力和数据处理能力的考查.

4.1 考查排列组合的内容

排列组合部分仍会突出对两个计数原理、排列组合等基本知识的考查,多以选择题、填空题为主,如2021年全国乙卷理科第6题.

4.2 考查二项式定理的内容

高考中对二项式定理的考查主要是基础知识和基本运算,以小题形式出现,没有难题.因为二项式定理的应用比较广泛,在复习过程中,我们还要关注与二项展开式中的系数有关的最值和二项式定理的逆用的问题.

4.3 考查概率的内容

概率部分试题形式基本稳定,考点比较集中,以传统优秀文化、生产生活实际为背景的概率问题屡见不鲜.古典概型、随机事件概率的计算和正态分布等考点均会出现在客观题中,2021年新高考Ⅰ,Ⅱ卷中是以多选题形式出现,考查的重点还是古典概型.如2019年全国Ⅰ卷理科第7题就是从我国古代典籍«周易»中的“卦”演变而来,需要考生认真审题与阅读,抓住概率类型,运用古典概型公式快速求解.条件概率、随机变量的分布列与数字特征、二项分布、超几何分布、正态分布仍然是命题的重点,且多以解答题形式出现.如2022年新高考Ⅰ卷第20 题,新高考Ⅱ卷第19题,全国甲卷理科第19题等对条件概率、随机变量分布列与数字特征、二项分布都进行了深入的考查.

4.4 考查统计的内容

统计思想与原理的广泛应用是数学与生产生活实际联系的重要纽带.在近几年的高考卷中,有关统计方面的试题更多关注时代热点,如新农村建设、医疗卫生、药品安全、质量检测等.如2018年全国Ⅰ卷理科第3题就是典型的新时代新农村经济建设问题,要求考生对现有数据进行分析与处理.

以频率分布直方图为背景考查离散型随机变量的概率分布列与期望的计算,突出考查学生应用数学意识解决实际生活问题的能力.以茎叶图为背景考查概率知识、2×2列联表考查独立性检验与概率知识等,这些问题着重考查学生从图表中获取信息、处理数据的能力.此类题在全国卷中多次出现,如2022年新高考Ⅰ卷第20题,以概率与统计模型为背景的创新题今后还会考查,值得我们关注.统计与函数相结合的概率统计题综合性强、难度大,最近出现的一次是2017年全国课标Ⅲ卷第19题.纯粹的统计学问题,如2016年全国课标Ⅲ卷文、理科第18题考查了生活垃圾无害化处理问题.

5 复习建议

概率与统计的知识点错综复杂又环环相扣,试题一般不是单独考查某一个知识点,而是对多个知识点的综合考查.因此在复习时,我们既要准确理解概念、公式与定理的含义,又要建构知识网络,厘清概念、公式与定理之间的逻辑联系.如概率的基本性质是基于事件关系这一个前提建立的,所以我们在学习概率的基本性质前必须理解随机事件这一基本概念.如果弄不清事件的关系,那么就难以正确理解和运用概率的基本性质,同时也会影响对二项分布、超几何分布的学习.

5.1 加强对概率、统计概念的精准理解,提升辨析概念的基本能力

概念是数学的细胞,是思维的载体,是创新的源泉.概念学习是学习数学的核心环节,整个数学知识体系是建立在概念基础之上的.因此,我们要注重对统计与概率知识的再挖掘.深入理解统计学原理,领悟统计学思想,不能只停留在记住结论、公式上,要弄清结论所反映的原理是什么、公式又是如何推导的.高考中往往以“统计”为背景考查“概率”,因而概率知识是不可忽视的,概率题的突破可以从概率模型入手,分概率模型训练.

5.2 重视阅读理解训练,培养数据处理及运算能力

图表中信息的读取、数据的处理是解决统计与概率问题的关键所在.在统计与概率试题中,一般题干文字较多、信息量较大、符号图表密集、参考数据冗长.读不懂题意是造成概率统计试题失分的主要原因之一,因此,我们要加强对阅读理解的训练,要学会三读:一读从统计图表中能直接看到的信息,二读经过简单分析后能得到的信息,三读超越数据本身的信息,在读的过程中学会归纳、分析、总结、反思.

5.3 注重回归教材与真题训练,提高解决实际问题的应用能力

教材是教学之本,不少高考题的原型都源自于教材中的例题、习题.学生在复习中一定要注重对教材例题、习题的探究和利用,同时,还要加强对高考真题的适时训练,并能从中发现试题的特点,悟出命题规律,进行有效复习.概率统计源自生产生活,同时又能解决生产生活中的实际问题.这些问题的设置要求考生对所给数据进行分析与处理,运用所学知识来解决实际问题,考查学生的应用能力.

(完)