强基计划数学备考系列讲座(12)——组合计数

王慧兴(正高级教师 特级教师)

(清华大学附属中学)

组合计数是强基计划校考的必考题目,但现行高中数学课标弱化了组合计数的教学要求.满足于常态数学学习难以应对强基计划校考,因此学生在强基备考时很有必要系统地掌握组合计数问题的探究、求解策略.

1 知识与技能

1.1 知识梳理

表1

1.2 要点解析

(1)满足不定方程x1＋x2＋…＋xn＝m(m,n∈N∗)的一个有序数组(x1,x2,…,xn),称为其一个解,其正整数解(xi∈N∗,i＝1,2,…,n)与非负整数解(xi∈N,i＝1,2,…,n)可以相互转化.现探求其正整数解个数,这里先给出一种求法——插板法.

把m＝1＋1＋…＋1想象成没有区别的m个小球,把变量x1,x2,…,xn想象成n个不同的盒子,转化为求把这m个相同的小球装入n个不同的盒子里的不同装法数.

我们先把m个相同的小球排成一行,只有1种方法,再从m－1个空隙里任选n－1个空隙插入没有区别的隔板,把小球分成n段,最后逐段依次定序装入n个盒子里,这种不同装法数就等于分段方法数,因此,按照方程对变量x1,x2,…,xn赋值得到的方程的正整数解(x1,x2,…,xn)个数就是,其中m＞n.

对方程x1＋x2＋…＋xn＝m的任一非负整数解(x1,x2,…,xn),由x1＋x2＋… ＋xn＝m,得(x1＋1)＋(x2＋1)＋…＋(xn＋1)＝m＋n,令xi＋1＝yi(i＝1,2,…,n),则(x1＋1,x2＋1,…,xn＋1)就是方程y1＋y2＋…＋yn＝m＋n的一个正整数解.这就给出原方程的非负整数解与新方程的正整数解之间的一一对应关系,所以原方程的非负整数解的个数是

(2)容斥原理:有限集合X的元素个数记作|X|,则n个有限集合Ai(1≤i≤n)的并集元素个数算法为

这个算法称为容斥原理,当其中任意两个集合交集都是空集时,就是加法原理.

(3)映射转移:两个有限集合A,B之间的映射f:A→B,如果f是单射,则|A|≤|B|;如果f是满射,则|A|≥|B|;如果f是双射,则|A|＝|B|;倍数映射——B中每个元素在A中都恰有k个原像,则|A|＝k|B|.

(4)转化化归:情境转化是组合计数常态,通过情境转化,在新情境中计数对象之间逻辑关系清晰,使得分步、分类变得容易,便于整体把握,从根本上化难为易.“转化化归”是一种思想、观点,“映射转移”就是一种典型的具体策略,“插板法”又是映射转移方法的一种具体表现.由于计数情境的多样性,转化化归不仅表现多样,而且往往富有技巧性.下面再给出探究上述不定方程两类解的个数的另一种转化方法.

记方程x1＋x2＋…＋xn＝m(m＞n)的所有正整数解构成集合A.任取(x1,x2,…,xn)∈A,则

换元,令(x1,x1＋x2,…,x1＋x2＋…＋xn－1)＝(y1,y2,…,yn－1),则得到一个定序排列1≤y1＜y2＜…＜yn－1≤m－1,记所有这种定序排列的集合为B,则这种换元建立了一个双射f:A→B,故方程的正整数解的个数为

记x1＋x2＋…＋xn＝m的所有非负整数解构成一个集合A′,任取(x1,x2,…,xn)∈A′,则

等价转化为

换元,令x1＋x2＋…＋xi＋i－1＝yi(1≤i≤n－1),得1≤y1＜y2＜…＜yn－1≤m＋n－1,所有这种定序排列构成的集合记作B′,得到双射f:A′→B′,故上述方程的非负整数解的个数为

(5)生成函数:又称母函数,把计数方法与特定多项式中某种项形成对应,但通常是多对一,甚至是所有方法与同一种项对应,因此所求计数结果等于所构造的多项式中对应项的系数.因此,母函数方法本质上也是转化化归思想的一种具体表现.读者可结合下文例15理解.

2 典例精析

2.1 计数基本技能

计数对象之间关联简单,计数逻辑清晰,分步与分类简单易行,历练这些方法是促进思维进阶、发展计数高阶思维必经环节.

1)穷举法

穷举法是一项基本技能,常用于元素不多的情境中.古典概型概率计算本质上是两个计数之比,但现行高中数学课标却要求先学习古典概型,后续再学习排列组合,就是强调教学必须重视引领学生历练、掌握穷举法.

例16位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13 次交换,则收到4 份纪念品的同学人数为( ).

A.1或3 B.1或4 C.2或3 D.2或4

由于|V|＝6,称图G(V,E)为6阶简单图,如果其中每两个顶点之间都连一条边,则称之为完全图,记作K6,其边数应当是,但这里|E|＝13,所以图G(V,E)可以从完全图K6中去掉两条边得到,而去掉两条边的方式有两种,如图1所示.

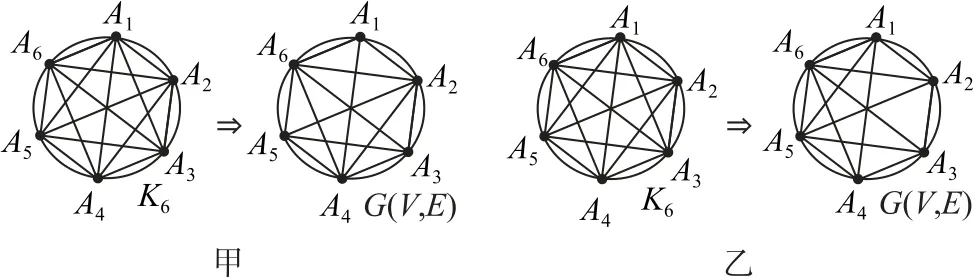
图1

在图1-甲中,从K6中删除有公共顶点的两条边A1A3,A1A5,得到图G(V,E),其度数(每个顶点引出的边的条数)序列为(d1,d2,d3,d4,d5,d6)＝(3,5,4,5,4,5);在图1-乙中从K6中删除无公共顶点的两条边A1A3,A2A4,得到图G(V,E),其度数序列为(d1,d2,d3,d4,d5,d6)＝(4,4,4,4,5,5).

综上,本题5阶简单图G(V,E)中度数是4的点数是2或4,故选D.

2)先组合后排列

例2安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( ).

A.12种 B.18种 C.24种 D.36种

3)特殊元素优先安排

例3用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ).

A.243 B.252 C.261 D.279

4)相邻元素捆绑处理

例4把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有_________种.

第一步,捆绑A,B整合成一个“新产品”的方法数是;第二步,把C之外的2件产品与“新产品”排成一列的方法数是;第三步,再把产品C插入已排好的4件产品之间的方法数都是(无论A在何处)种方法.由分步乘法原理,满足题意的5件产品摆放方法数是

5)隔离问题插空处理

例5某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( ).

A.72 B.120 C.144 D.168

第一类,把2个小品类节目与1个相声类节目排入3个舞蹈节目的两个空隙与两端之一,共有种方法.

第二类,把1个相声节目与两个小品类节目之一重组在一起使之相邻,重组的方法共有,再以两个元素排入3个舞蹈节目之间的两个空隙有种插入方法,这一类不同方法数是.

6)分排问题直排处理

例6如图2所示,在一次射击比赛中,有8个泥质靶子挂成3列,一位神枪手按如下规则打掉所有靶子:首先选择将要有一个靶子被打掉的一列;然后在被选列中打掉尚存的最下面一个靶子.求打掉这8个靶子共有多少种不同的顺序.

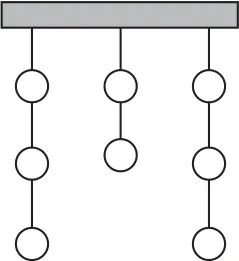
图2

7)正难则反,转化情境

例7把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有________种.

因为A,B已经相邻,所以总控数据汇总C与A相邻的情形一定是B位于A,C之间的ABC或CAB两种固定结构,以这两种固定结构之一与另外两个自由产品任意排成一列的摆法是,所以总控数据中A与C相邻的摆法是.

综上,分离出满足题设条件的产品摆法是

2.2 分步与分类

计数对象之间“胶着纠缠”“不独立”,难以用一个组合数或排列数直接给出算法,分步与分类就成为求解组合计数问题的常态技能.

例8定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0的个数不少于1的个数.若m＝4,则不同的“规范01数列”共有( ).

A.18个 B.16个 C.14个 D.12个

第一类,前4项都是0,后4项都是1,这样的“规范01数列”个数只有1个.

第二类,前4项中a2,a3,a4恰有1个1,后4项中a5,a6,a7恰有1个0,这样的“规范01数列”个数是

第三类,前4项中恰有2个1,这2 个1 只能是a2＝a4＝1或a3＝a4＝1,因此,前4项安排方法数是;后4项中恰有2个0,这2个0只能是a5＝a6＝0或a5＝a7＝0,后4项安排方法数是,因此,这样的“规范01数列”个数是

综上,由分类加法原理,满足题设条件的“规范01数列”个数是,故选C.

例9(北京大学)将不大于12的正整数分为6个两两交集为空集的二元集合,并且每个集合中的两个元素互质,则不同的分法有________种.

因为C＝{2,4,6,8,10,12}中任意两个元素都不互质,所以这6个数分别属于6个不同的子集,记

其中i∈Ai(i∈C).其余元素1,7,11可以任意放入每一个子集中,但5∉A10,3和9∉A6∪A12.分类计数:

情形一,5∈A6∪A12,这时3 和9∈A2∪A4∪A8∪A10,1,7,11 任意放,所以这一类的划分个数为

情形二,5∉A6∪A12,则5∈A2∪A4∪A8,3和9含于A2,A4,A8不含5的另外2个连同A10之中,1,7,11可以任意放,所以这一类划分的个数为

2.3 容斥计数

例10(上海交通大学)在小于1000的正整数中,既不是5 的倍数也不是7 的倍数的整数个数是________.

2.4 映射转移

计数对象之间“胶着”,关联性强,算法逻辑不清晰,计数情境转换就成为探求复杂计数问题的方法.

例11(清华大学)已知集合A,B,C⊆{1,2,…,2020},且A⊆B⊆C,则有序集合组(A,B,C)的个数是________.

由分步乘法原理,这种映射的个数是42020,所以满足题设条件的有序集组(A,B,C)的个数是42020.

2.5 递推传递

例12(中国科学技术大学)设k(k≥3)个人进行互相传球游戏,每个拿球的人等可能地把球传给其他人中的任何一位.若初始时,球在甲手中,则第n次传球后,球又回到甲手中的概率为________.

2.6 重建模型

重建模型是积极地改进算法,追求更为快捷、清晰的算法的永恒追求,也是映射转移计数的一种具体表现.

例13(上海交通大学)两条异面直线称为一个异面直线对,连接正方体的8个顶点得到的所有直线中,异面直线对的个数是_________.

因为任一四面体ABCD的六条棱都可以构成3个异面直线对“AB与CD、AC与BD、AD与BC”,而从正方体的8个顶点中任取4个顶点所得的个四点组中共有个不共面四点组,这些四点组都可以作为四面体的四个顶点,也就是四面体的个数,故所求异面直线对个数是

下面用古典概型计算几何概型,这是基于对称性处理重建模型、改善计数情境转化的一种常用策略.

例14(中国科学技术大学)在圆周上独立随机取n个点,求此n个点可被半圆周覆盖的概率P.

2.7 生成函数

例15(上海交通大学)从2个红色球、3个黑色球、5个白色球(同色球完全相同)中任意取出6个,则不同取法种数是________.

因为展开式通项为xixjxk,其中i∈{0,1,2},j∈{0,1,2,3},k∈{0,1,2,3,4,5},所以x6的系数就是方程i＋j＋k＝6满足条件“i≤2,j≤3,k≤5”的非负整数解(i,j,k)的个数.

按i∈{0,1,2}枚举可得这种有序非负整数三元组(i,j,k)的个数是3＋4＋4＝11,故满足题设条件取出6个球的方法数是11.

2.8 化归转化

例16(清华大学)给定一个圆周上十个等分点Ai(1≤i≤10),则取其中的四个,得到等腰梯形的四个顶点的取法数是( ).

A.60 B.45 C.40 D.50

上面定义的正整数有序三元组(x,y,z)由条件确定,枚举可得所有(x,y,z)共有6个:(1,1,7),(2,1,6),(3,1,5),(1,2,5),(2,2,4),(1,3,3),所以可以得到等腰梯形四个顶点的取法数是10×6＝60,故选A.

例17(复旦大学)方程18x＋4y＋9z＝2021的正整数解(x,y,z)的个数是________.

模9,得4y≡5(mod9),即y≡－1(mod9),y＝9y′－1(y′∈N∗),所以原方程化为18x＋4(9y′－1)＋9z＝2021 ⇔2x＋4y′＋z＝225,从而z是奇数,记z＝2z′－1(z′∈N∗),方程继续转化为x＋2y′＋z′＝113,从而x＋z′必为奇数,即x,z′一奇一偶,由对称性,这两种情形的解数一样多.

不妨设x是奇数,记x＝2x′－1,z′＝2z″(x′,z″∈N∗),继续转化上述方程,得x′＋y′＋z″＝57,该方程的正整数解(x′,y′,z″)的个数是,对应地确定个原方程的正整数解(x,y,z)＝(2x′－1,9y′－1,4z″－1),故原方程的正整数解(x,y,z)个数是

2.9 换序计数

例18给定正整数n,集合S＝{1,2,…,10}的所有有序子集组(A1,A2,…,An)构成一个集合T,则的值是_________.

另一方面,对任一a∈S,含这个a的所有有序子集组(A1,A2,…,An)的个数是

因此,所有n＋1元组(A1,A2,…,An,a)的个数为

由①②,得

3 实战演练

1.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成_________个没有重复数字的四位数(用数字作答).

2.把5个不同的小球装入4个不同的盒子,要求每个盒子至少装入1个球,则不同装法有________种.

3.某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( ).

A.36种 B.42种 C.48种 D.54种

4.(北京大学)已知五项正整数数列{an}:a1,a2,a3,a4,a5,满足|ak＋1－ak|≤1(k＝1,2,3,4),其中存在一项的值是3,则这种数列的个数为_________.

5.(复旦大学)某公司安排甲、乙、丙等7人完成7天的值班任务,每人负责1天.已知甲不安排在第一天,乙不安排在第二天,甲和丙安排在相邻两天,则不同安排方式的种数是_________.

6.(上海交通大学)2 条抛物线最多分平面为7份,3条最多分16份,则4条抛物线最多把平面分成_________份.

7.(复旦大学)方程3x＋4y＋12z＝2020的非负整数解(x,y,z)的个数是________.

8.(北京大学)如果一个十位数F的各位数字之和等于81,则称F为一个“好数”,则所有好数的个数为________.

9.(北京大学)现有7把钥匙,用这些钥匙随机开锁,则D1,D2,D3这三把钥匙不能打开对应的锁的概率是_________.

10.(北京大学)从一个六元集合到一个三元集合的满射个数是________.

答案1.1260. 2.240. 3.B. 4.211. 5.1128 .6.29. 7.14365. 8.48619. 9.

(完)