Bifurcation Analysis and Bounded Optical Soliton Solutions of the Biswas-Arshed Model

Fahad Sameer Alshammari,Md Fazlul Hoque, Harun-Or-Roshid and Muhammad Nadeem

1Department of Mathematics,College of Science at Alkharj,Prince Sattam bin Abdulaziz University,Alkharj,11942,Saudi Arabia

2Department of Mathematics,Pabna University of Science and Technology,Pabna,6600,Bangladesh

3Faculty of Science,Yibin University,Yibin,644000,China

ABSTRACT We investigate the bounded travelling wave solutions of the Biswas-Arshed model(BAM)including the low group velocity dispersion and excluding the self-phase modulation.We integrate the nonlinear structure of the model to obtain bounded optical solitons which pass through the optical fibers in the non-Kerr media.The bifurcation technique of the dynamical system is used to achieve the parameter bifurcation sets and split the parameter space into various areas which correspond to different phase portraits.All bounded optical solitons and bounded periodic wave solutions are identified and derived conforming to each region of these phase portraits.We also apply the extended sinh-Gordon equation expansion and the generalized Kudryashov integral schemes to obtain additional bounded optical soliton solutions of the BAM nonlinearity.We present more bounded optical shock waves, the bright-dark solitary wave,and optical rogue waves for the structure model via these schemes in different aspects.

KEYWORDS The Biswas-Arshed model;the extended sinh-Gordon equation expansion;the generalized Kudryashov approach;shock wave double solitons;optical singular double solitons;chirp-free bright-dark double solitons

1 Introduction

The study of optical solitons and their applications in the account of optical fiber transmissions is a paramount topic in communication networks.The general concepts of transmission optical solitons in nonlinear optical fiber systems are fundamentally important in controlling optical continuum creation and transferring information over very long distances.The general nonlinear complex models(see[1-7]) are the best examples of the exploration and description of the effect on the picosecond vibration with the group velocity dispersion(GVD)as well as the self-phase modulation(SPM).Such models can be used to explicitly address the electro-magnetic waves with ultrashort pules that can cover the world within a nanosecond.Thus these varieties of waves have been highly studied in the communication technologies,especially,in the optical fibers,data transmissions,telecommunication sectors,transoceanic spaces and so on[6-10].Recently,Biswas and Arshed introduced a model which is greatly interesting due to the consideration of minor GVD and neglecting the SPM[1].A number of works have done on this model to investigate optical solitons by using various approaches such as the trail solution technique[12],modified simple equation technique[13],Kerr and power law nonlinearity[14,15],mapping method[16],the extended trial function method[17],parameter restriction approach[18]and theexpansion approach[19].They also pointed out the bright,singular and combosolitons for the two integration structures of the model.It is fundamentally effective in investigating the dynamical bounded and unbounded solitons in optical fibers and metameterials in case of both low GVD and nonlinearity via new effective approaches.Young dynamical researchers established more new effective schemes to obtain various types of optical solitons like the generalized Kudryashov(GK) approaches [20,21], the Jacobian elliptic function method [22], the extended sinh-Gordon equation expansion method [23], Hirota bilinear scheme [24,25], Darboux transformation method[26],dynamical system approaces[27],solitary waves travel in a porous medium or along an unsmooth boundary[28,29]and so on.Although all those approaches have derived many profound results,some bounded optical wave solutions could still be an unexplored subjects via dynamical scheme with a bifurcation of the BAM.

The purpose of this paper is to show how we can present optical shock wave including both bright and dark, optical soliton solutions, and construct the periodic wave solutions via dynamical system method with bifurcation analysis for the model.We also use the extended sinh-Gordon equation expansion(EShGEE)and the generalized Kudryashov(GK)approaches[20,21]to get a more bounded wave solution.To our knowledge, these types of investigations for the BAM are the first step in the study of the dynamical system,EShGEE and the GK methods.

2 The Biswas-Arshed Model

The Biswas-Arshed model(BAM)[11]is given as the following form:

whereΨ(x,t)is the wave function of soliton anda1,a2,b1,b2are,respectively,the GVD coefficient,the spatio-temporal dispersion,the third-order dispersion coefficient,and the spatio-temporal third-order dispersion coefficient.In the modelεrepresents self-steepening andσ,ϑare dispersion effects.Biswas and Arshed first explored this model in the context of higher-order dispersions with minor self-phase modulation.The optical solutions of the model with transmission wave have been retrieved in the point of view of Kerr and non-Kerr law[14].Recently,the effect of the optical shock wave,optical solitons,rogue waves and their various interactions were investigated in[19].In this paper,we revisit this model as it has wider applicability,and many other aspects such as bright and dark,optical soliton and the periodic wave solutions of the BAM by the method of a dynamical system with bifurcation analysis,the EShGEE and the GK methods still remain.In the following section, we use the transformation variable to Eq.(1).

2.1 The Structure of BAM

The transformation variable[11]

whereΦ(ζ)is the amplitude portion withζ=x-δt,the phase componentχ(x,t)=-kx+wt+ρ,where the constantsδ,ρ,w,kare,respectively,the soliton velocity,the phase constant,the wave number and the frequency of the soliton,convert the nonlinear evaluation Eq.(1)to an ordinary differential equation.After a long computation and an integration,one can present the differential equation of Eq.(1)[11,14]as follows:

One can easily find the following conditions that satisfies the Eq.(4):δ=b1/b2,b2δk2-3b1k2+2b2wk-δ+2a2δk-2a1k+a2w=0 and 2σ+ϑ+3ε=0.

Thus,we have to analyze the Eq.(3)only.In the following subsection,we analyze bifurcation to acquire phase portraits to identify the number and types of solutions that exist for the model.Beside this,we apply three different techniques,namely,the dynamical,the EShGEE and the GK approaches to the corresponding model Eq.(3)in order to obtain the corresponding exact optical soliton solutions of Eq.(1).

2.2 Bifurcations Analysis of the BAM

We first consider the bifurcations of phase orbits of ordinary differential equation(ODE)Eq.(3).To proceed of the motive,we need to convert the second order ODE to a dynamical system,which is possible by settingΦ＇=Θin the ODE.In this case the ODE in Eq.(3)takes the form of a dynamical system:

with the Hamiltonian

whereP=a1-a2δ+3b1k-2b2δk-b2w,Q=a1k2-a2wk+b1k3-b2wk2+wandR=k(ε+ϑ).

Setting the system of Eq.(5)to zero gives critical pointsO(0,0),Determinants of Jacobian matrices at the three equilibrium points are:and

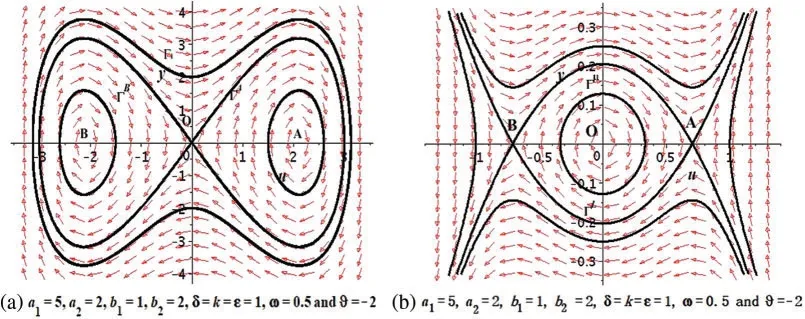
Figure 1:Bifurcation of system Eq.(5)with ＜0: (a)for ＞0(b)for ＜0 at x=t=1

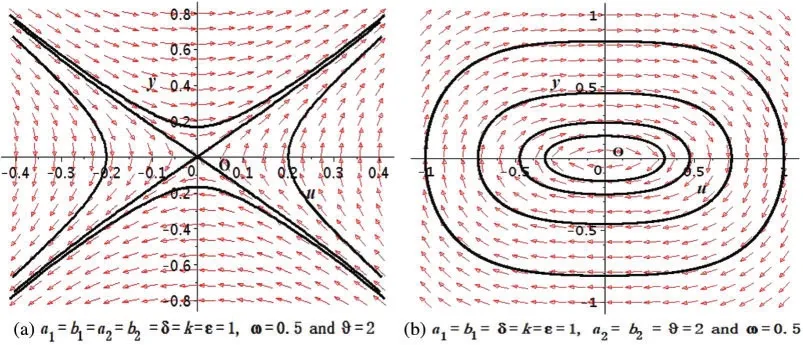
Figure 2:Bifurcation of system Eq.(5)with ＞0:(a)for ＞0(b)for ＜0 at x=t=1

Moreover,a different dynamical system can arise forQ=0,which reads

with the Hamiltonian

It has a unique critical pointA(0,0)of higher order withdetP=0.From the theorem-2 of[27],we getandbn=0.It yields thatAis a saddle point when(see the Fig.3a)and A is a critical point when(see the Fig.3b).We observe that all bounded orbits and traveling wave solutions can be simulated on the phase portraits.All bounded orbits and travelling wave solutions can be simulated.

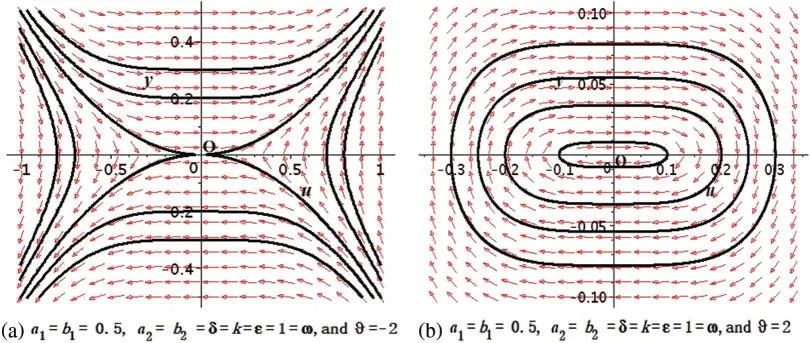
Figure 3:Bifurcation of system Eq.(5)with Q =0:(a)for ＞0(b)for ＜0 at x=t=1

2.3 Bounded Travelling Wave Solutions of BAM

This section will provide the explicit expressions of all bounded travelling wave solution of the system Eq.(5).

2.3.1 The Periodic Wave Solution

wherel ＜m ＜n ＜Φ ＜r.Let us consider the periodicity of the orbit is 2T1and initial valueΦ(0)=n,we have

Combining Eqs.(12)and(13),it leads to

By the direct elliptic integral and calculation,we arrive at the solution

Similarly,the periodic solution corresponding toΓBcan be expressed as

wherel ＜Φ ＜m ＜n ＜r.Taking period is 2T2and initial conditionΦ(0) =l, we arrive at the solution

Again,recall the casesdfracQR ＜0 andthere is class of periodic orbitsΓOenclosingO.The corresponding wave solutions via Eq.(6)closed orbitΓOare as follows:

wherel ＜m ＜Φ ＜n ＜rwhich are real valued constants.Let us consider the periodicity of the orbit is 2T3and initial valueΦ(0)=m,we obtain

Combining Eqs.(20)and(21),it leads to

Again by the elliptic integral and after some calculation,we arrive at the solution

2.3.2 The Solitary Wave Solutions

where-l ＜Φ ＜l.Setting the homoclinic orbit and initial valueΦ(0)=m,we obtain

Applying the elliptic integral and some calculation,we arrive at the solution

The resulting solutionΦ4comes due to the homoclinic orbitΓAfor the system Eq.(5)by(6)and it expresses the bright peaked soliton, i.e., bright peakon.Now, the corresponding bounded optical soliton solution will come through the relation Eq.(2)with modulus as|Ψ4(x,t)|,which is also a bright optical peakon soliton.

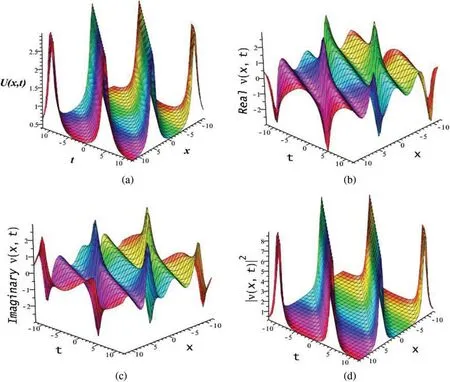
Figure 4:(a)Periodic wave for+via Eq.(15),(b)real part of Ψ1(x,t)for Eq.(15),(c)imaginary part of Ψ1(x,t)for Eq.(15)and(d)optical bright waves|Ψ1(x,t)|2 for the parametric values a1 = 5,a2 =b2 =2,b1 =δ =k=ε =1,w=0.5,ϑ =-2,l =0.2,m=0.3,n=0.4,r=3

Similarly,let the homoclinic orbit and initial valueΦ(0)=-m,we obtain

Through the elliptic integral and after some calculation,we arrive at the solution

The obtained solutionΦ5comes due to the homoclinic orbitΓBfor the system Eq.(5)by Eq.(6)and it expresses the dark peaked soliton,i.e.,anti-peakon.Now,the corresponding bounded optical soliton solution will arise through the relation Eq.(2) with modulus as |Ψ5(x,t)|, which is also a bright optical peakon soliton.The nature of the peaked solitons and its optical peaked solitons are demonstrated via the Figs.5 and 6 forΦ4(x,t),Ψ4(x,t)andΦ4(x,t),Ψ4(x,t)respectively.To investigate the all propagation properties of the wave,we illustrate here the 3D plots ofΦ4(x,t),Φ5(x,t),real part,imaginary part and square of modulus of|Ψ4(x,t)|,|Ψ5(x,t)|in Figs.5 and 6a-6d,respectively.

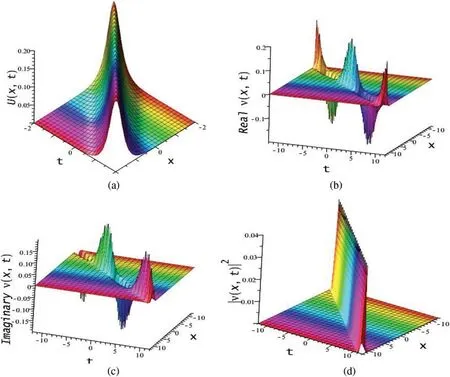
Figure 5:(a)Bright peaked soliton via Eq.(27),(b)Real part of Ψ4(x,t)for Eq.(27),(c)Imaginary part of Ψ4(x,t)for Eq.(27)and(d)Optical bright peaked soliton|Ψ4(x,t)|2 for the parametric values a1 =5,a2 =b2 =2,b1 =δ =k=ε =1,w=0.5,ϑ =-2,l =0.2,m=5

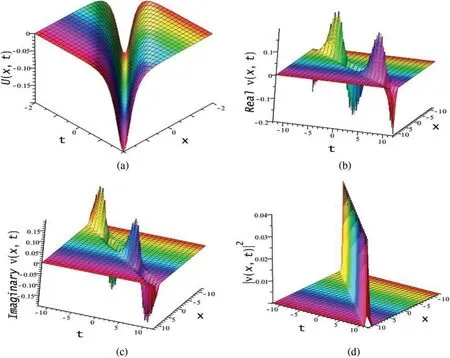
Figure 6: (a) Dark peaked soliton via Eq.(29), (b) Real part of Ψ4(x,t) for Eq.(29), (c) Imaginary part of Ψ4(x,t)for Eq.(29)and(d)Optical bright peaked soliton|Ψ4(x,t)|2 for the parametric values a1 =5,a2 =b2 =2,b1 =δ =k=ε =1,w=0.5,ϑ =-2,l =0.2,m=5

2.3.3 The Shock Wave Solutions

and applying the elliptic integral and after some calculation,we arrive at the solution

Noting that

The resulting solutionΦ6(x,t)comes in-terms oftanh-function due to the heteroclinic orbitΓμfor the system Eq.(5)by Eq.(6)and it expresses the kink type shock wave,and its corresponding bounded optical soliton solution will arise through the relation Eq.(2) with modulus as |Ψ6(x,t)|, which is a bounded optical dark peaked soliton,i.e.,anti-peakon.The nature of this soliton is specified in Figs.7a and 7b forΦ6(x,t)and|Ψ6(x,t)|2,respectively.Moreover,the resulting solutionΦ7(x,t)(depicted in 7c)comes in-terms oftanh-function due to the heteroclinic orbitΓLfor the system Eq.(5)by Eq.(6),and it expresses the anti-kink type shock wave and its corresponding bounded optical soliton solution comes through the relation Eq.(2) with modulus as |Ψ7(x,t)|2(depicted in Fig.7d), which is also a bounded optical dark peaked soliton,i.e.,anti-peakon.

Figure 7:(a)Shock wave(kink)via Φ(x,t)for Eq.(33),(b)Optical anti-peakon|Ψ6(x,t)|2 for Eq.(29),(c) Shock wave (anti-kink) via Φ(x,t) for Eq.(29) and (d) Optical anti-peakon |Ψ7(x,t)|2 for the parametric values a1 =b1 =δ =k=ε =1,a2 =b2 =2,w=0.5,ϑ =-2

2.4 Optical Soliton Solutions to BAM via the EShGEE

One considers the general form of the trail solution in the extended sinh-Gordon equation expansion approach(EShGEE)[23],

whereM0,Mr,Lr,r=1,2,...,nare free constants to be later calculated,and the ⊖is a function ofζ,which satisfies the condition,

Due to balance principal,the valuenof Eq.(35)can be obtained.The Eq.(36)has been obtained from the sinh-Gordon equation[23],

and they[23]obtained the solutions,

and

We now compute the balance number of Eq.(3), which leads ton= 1.Then the trail solution Eq.(35)in the EShGEEM takes the form,

Putting Eq.(40)into Eq.(3)along with Eq.(36),we obtain a polynomial of sinh(ζ)and cosh(ζ)functions,whose equating coefficients lead to a system of equations,and the solutions of the system of equations yield the following constraints:

whereM1presents arbitrary constant andΓ1=(εk3M21b2+k3ϑM21b2+εk2M21a2+k2ϑM21a2+2εkM21b2-4k3b1b2+2kϑM21b2-εkM21-6k2a2b1-kϑM21-2ka1a2+6b1k+2a1),andΓ2=2εk3M21b2+2k3ϑM21b2+2εk2M21a2+2k2ϑM21a2+εkM21b2-2k3b1b2+kϑM21b2-2εkM21-3k2a2b1-2kϑM21-ka1a2+3kb1+a1.

Now for the Set 1,if we combine Eq.(41)with Eqs.(38)-(40),and substituting into Eq.(2),we obtain the exact soliton solutions of Eq.(1).These solutions of the model give us the optical shock wave and optical singular shock solitons,

whereδandwcome from Eq.(41).In the Eq.(44),Φ(x,t) comes in terms oftanh-function which presents kink shock waves.This solution presents a kink shock wave for the positive taking sign in the results (see Fig.8a) but taking negative sign it presents an anti-kink shock wave (see Fig.8b).The corresponding optical solitons represent dark-bell type peaked soliton(see Fig.8c).On the other hand,in the Eq.(45),Φ(x,t)comes in terms ofcoth-function which presents kink shock waves with singularities i.e.,singular kink type shock wave,for the positive sign it expresses singular kink but for the negative sign,it presents singular anti-kink type shock wave.The corresponding optical solitons represent bright peaked solitons with singularities(see Fig.8d).

Similarly,for the Set 2,if we combine Eq.(42)with Eqs.(38)-(40),and substituting into Eq.(2),we obtain the exact soliton solutions of Eq.(1).These solutions give us the combination of chirp-free bright and optical shock wave double solitons,and the combination of optical singular double solitons,

whereδandwcome from Eq.(42).And for the Set 3,if we combine Eq.(43)with Eqs.(38)-(40),and substituting into Eq.(2),we obtain the exact soliton solutions of Eq.(1).These solutions are able to give the combination of chirp-free bright and optical shock wave double solitons,and the combination of optical singular double solitons,

whereδandwcome from Eq.(43).The nature of solutionsΨ12,13(x,t) andΨ16,17(x,t) are similar as they comes from produce periodic exponential function with linear combinations ofsech-function(give bell solitonic nature) andtanh-function (give kink shock solitonic nature).Thus, the resulting nature of all the solutions is periodic bell wave with at least one kink in the surface depicted by the real part ofΨ17(x,t)in Fig.9a and square of modulus ofΨ12(x,t)in Fig.9b.We see that the square of modulus give us many small amplitude waves which can propagate to transmit signal rapidly through optical fiber.Besides this, the solutionsΨ14,15(x,t) have the same properties that they exhibits mutipeaked optical solitonic nature in presence of singularities.This character is displayed in Fig.9c via|Ψ14(x,t)|2.The solutionsΨ18,19(x,t)have the same properties that they exhibits dark bell optical soliton in presence of singularities.This character is displayed in Fig.9d via|Ψ18(x,t)|2.

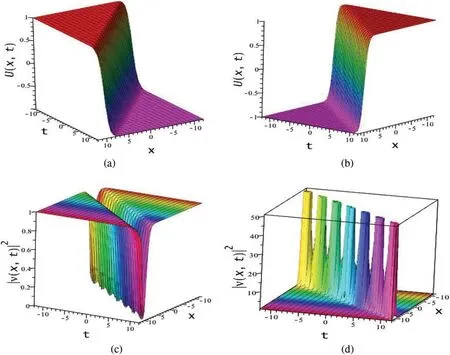
Figure 8: (a) Shock wave (Kink) for + via (tanh) of Eq.(44), (b) Shock wave (anti-kink)for-via (tanh) of Eq.(44), (c) Optical dark peakon via (tanh) of Eq.(44) and (d) Optical bright peaked (anti-peakon) with singularities Eq.(45) for the parametric values a1 =5,a2 =b1 =b2 =h=2,b1 =δ =k=ε =1,w=0.5,ϑ =-2,L1 =2,M1 =1

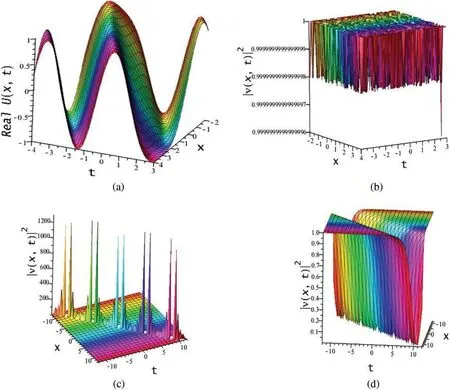
Figure 9: (a) Combine bell kink soliton comes from real part of |Ψ17(x,t)|, (b) Small amplitude response |Ψ12(x,t)|2, (c) Multi-peaked optical soliton with singularities via Ψ14(x,t) and (d) Dark bell optical soliton with singularities via Ψ18(x,t) for the parametric values a1 = 5,a2 = b2 = 2,b1δ =k=ε =M1 =1,w=0.5,ϑ =-2

2.5 Optical Soliton Solutions to the Biswas-Arshed Model via the GK Method

The GK method[30]is a unique approach to obtaining the generalized solitons and periodic rogue waves of the nonlinear evolution equations(NLEEs)[20,21].We now consider a rational series in this method as:

whereMr,Ll,are constants to be later calculated andMn≠0,Lm≠0.The functionF(ζ)satisfies the Ricatti equation,

with the solution

wherehis the integral constant.

The trail solution Eq.(50)to the BAM takes the following form for the balance numbersn= 2 andm=1,

Putting Eq.(53)into Eq.(3)along with Eq.(51),we obtain a polynomial ofF(ζ)functions,whose equating coefficients lead to a system of equations,and provide the following set of constraints:

whereL1,M1are constants andΛ1=2εk3M21b2+2k3ϑM21b2-2k3L21b1b2+2εk2M21a2+2k2ϑM21a2-3k2L21a2b1+εkM21b2+kϑM21b2-kL21a1a2-2εkM21-2kϑM21+3kL21b1+L21a1.

whereL0,M1are constants andΛ2=εk3M21b2+k3ϑM21b2- 16k3L20b1b2+εk2M21a2+k2ϑM21a2-24k2L20a2b1-εkM21b2-kϑM21b2-8kL20a1a2-εkM21-kϑM21+24kL20b1+8L20a1.

whereL0,M0are constants andΛ3=εk3M20b2+k3ϑM20b2- 4k3L20b1b2+εk2M20a2+k2ϑM20a2-6k2L20a2b1+2εkM20b2+2kϑM20b2-2kL20a1a2-εkM20-kϑM20+6kL20b1+2L20a1.

whereL0,L1,M0are constants andΛ4=2εk3M20b2+2k3ϑM20b2-2k3L20b1b2+2εk2M20a2+2k2ϑM20a2-3k2L20a2b1+εkM20b2+kϑM20b2-kL20a1a2-2εkM20-2kϑM20+3kL20b1+L20a1.

Now for the Set 1,if we combine Eq.(54)with Eq.(53)and substituting into Eq.(2),we obtain the exact soliton solutions of Eq.(1).These solutions are able to give us optical rogue wave solitons,

whereδandwcome from Eq.(54)andF(x-δt)comes from Eq.(52).

The behavior of the solutionΨ20(x,t) via Eq.(58) comes from produce periodic exponential function and exponential function (give solitonic nature).Thus, the resulting nature of the solution is periodic wave with a single shock(anti-kink)wave in both the real and imaginary parts,illustrated in Figs.10b and 10c.But the simpleΦ(x,t)and square of modulus ofΨ20(x,t)exhibits anti-kink type shock wave response in Figs.10a and 10b,respectively.

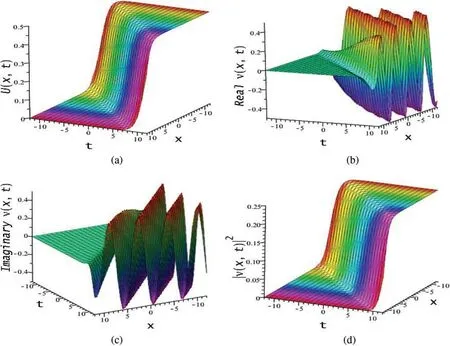
Figure 10:(a)Shock wave,(b)Real part of,(c)Imaginary part of and(d)Shock wave of Eq.(58)for the parametric values a1 =a2 =b1 =δ =k=ε =1,b2 =h=2,w=0.5,ϑ =-2,L1 =2,M1 =1

Similar,for the Set 2,if we combine Eq.(55)with Eq.(53)and substituting into Eq.(2),we obtain the exact soliton solutions of Eq.(1).These solutions lead to optical rogue wave solitons,

whereδandwcome from Eq.(55)andF(x-δt)from Eq.(52).For the Set 3,if we combine Eq.(56)with Eq.(53) and substituting into Eq.(2), we obtain the optical rogue wave soliton solutions of Eq.(1),

whereδandwcome from Eq.(56),andF(x-δt)from Eq.(52).And for the Set 4,combining Eq.(57)with Eq.(53) and substituting into Eq.(2), we obtain the optical rogue wave soliton solutions of Eq.(1),

whereδandwcome from Eq.(57)andF(x-δt)from Eq.(52).The behavior of the solutionΨ21(x,t),Ψ22(x,t) andΨ23(x,t) are same with singularities arises forL0= 0 or {1 - 2F(x-δt)} = 0.Since the resulting solution via Eqs.(59)-(61) comes from produce periodic exponential function and exponential function (give solitonic nature).Here, we reveal the results of Eq.(61) only against the three solutions, which exhibits a periodic wave with a singular shock wave in the both real and imaginary parts, illustrated in Fig.11b and 11c.But the simpleΦ(x,t) presents singular kink type shock wave (Fig.11a) and the square of modulus ofΨ23(x,t) exhibits multi-peaked optical soliton with more singularities(Fig.11d).

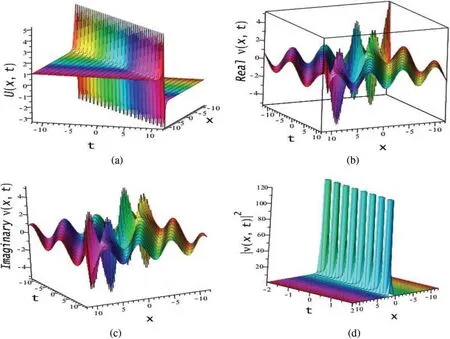
Figure 11: (a) Shock wave with singularity, (b) Real part of, (c) Imaginary part of and (d) Singular bright soliton of Eq.(61) for the parametric values a1 = a2 = b1 = δ = k =ε =1,b2 =h=2,w=0.5,ϑ =-2,L0 =M0 =1

3 Results and Discussions

This section will provide some discussions of the physical importance of the acquired results.The results of the BAM structure presented in this research have richer physical structure than earlier outcomes in the literature[11-18].The recorded solutions are significant in the context of nonlinear dynamics,physical science,mathematical physics and the optical communication through optical fiber.We studied BAM given by Eq.(1) using bifurcation analysis, dynamical system, EShGEE and GK schemes.The bifurcation scheme provided us the evidence of the existence of various periodic wave and optical soliton solution splitting parametric areas shown in different phase portraits in Figs.1 and 3 of the BAM.We also illustrated the physical meaning of the obtained explicit solutions 3D and contour plots that appeared in Figs.4 and 11.

4 Conclusion

The main results of this paper are on the application of the bifurcation analysis via a dynamical system scheme and the derivation of all bounded optical wave solutions of the Biswas-Arshed model.We obtained all types of phase portraits and corresponding bounded optical shock wave, bounded solitary wave,and the bounded periodic wave solutions of the BAM by using the dynamical scheme,the extended sinh-Gordon equation expansion,and the generalized Kudryashov integral schemes.To our knowledge, these types of solitons for the Biswas-Arshed model have not been explored before[13-16,19].All the solutions are illustrated graphically.The model could be investigated to get multisoliton and rogue wave solutions by the other existing methods,in particular,Hirota bilinear approach[24,25] and Darboux transformation [26].The results would be interesting to use in social media,telecommunication industries,internet zone,and many other aspects.

Acknowledgement:The authors thank to Prof.Ji-Huan He for his valuable suggestions that helped us in improving the quality and presentation of this paper.

Funding Statement:This research was supported by the Deanship of Scientific Research,Prince Sattam bin Abdulaziz University,Alkharj,Saudi Arabia,under Grant No.2021/01/19122.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.