Notes on Curves at a Constant Distance from the Edge of Regression on a Curve in Galilean 3-Space G3

Ali akmak,Sezai Kızıltu and Gkhan Mumcu

1Department of Mathematics,Faculty of Arts and Sciences,Bitlis Eren University,Bitlis,13000,Turkey

2Graduate School of Natural and Applied Sciences,Erzincan Binali Yıldırım University,Erzincan,24002,Turkey

3Department of Mathematics,Faculty of Arts and Science,Erzincan Binali Yıldırım University,Erzincan,24002,Turkey

ABSTRACT In this paper,we define the curve rλ = r+λd at a constant distance from the edge of regression on a curve r(s)with arc length parameter s in Galilean 3-space.Here,d is a non-isotropic or isotropic vector defined as a vector tightly fastened to Frenet trihedron of the curve r(s)in 3-dimensional Galilean space.We build the Frenet frame{Tλ,Nλ,Bλ}of the constructed curve rλ with respect to two types of the vector d and we indicate the properties related to the curvatures of the curve rλ.Also, for the curve rλ, we give the conditions to be a circular helix.Furthermore, we discuss ruled surfaces of type A generated via the curve rλ and the vector D which is defined as tangent of the curve rλ in 3-dimensional Galilean space.The constructed ruled surfaces also appear in two ways.The first is constructed with the curve rλ(s)=r(s)+λT(s)and the non-isotropic vector D.The second is formed by the curve rλ = r(s)+λ2N +λ3B and the non-isotropic vector D.We calculate the distribution parameters of the constructed ruled surfaces and we show that the ruled surfaces are developable.Finally,we provide examples and visuals to back up our research.

KEYWORDS Edge of regression;Galilean space;curvature;helix;ruled surface

1 Introduction

Klein pronounced a different definition of geometry in his introductory speech at the University of Erlangen in 1872.He explained that geometry,given by a subgroup G of a set and its symmetries,is the examination of invariants under this group[1].This concept was first presented in a lecture,and it resulted in the emergence of numerous geometries.Galilean geometry is one of these geometries whose motions are the Galilean transformations of classical kinematics.Yaglom explained the basics of Galilean geometry in 1979[2].Then particularly,the geometry of ruled surfaces in this space has been largely improved in Rschel’s thesis[3].

One of the important research areas in differential geometry is the theory of curves examined in various spaces.In particular,it has been examined in a lot of papers and remarkable results have been obtained in the 3-dimensional Galilean space[4-10].

The notion of the curves at a constant distance from the edge of regression has been introduced by Vogler.He has studied the curves traced on a torse at a constant distance from its edge of regression.The torse of a space curve in E3is dual to its pseudo-rectifying torse[11].Later,Hacısaliholu obtained a more general case of Vogler’s results[12].

This subject has been studied in Euclidean 3-space since the 1970s,and it is a method that generates a new curve from the curve through the Frenet frame of the curve.For the first time,we will discuss this issue in 3-dimensional Galilean space.While the curve is produced by using the unit vector which is defined by the Frenet frame apparatus of a curve in Euclidean 3-space,we will have produced the curve by considering two situations in the Galilean 3-space.This is because,in Galilean space,vectors are treated in two ways,isotropic and non-isotropic.

In this paper,we first recall the essential preliminaries on the Galilean 3-space.Then,we define curves in the Galilean 3-space and give the curvature properties of these curves.In the main part of our study,we define a curve noted byrλat a constant distance from its edge of regression on a unitspeed admissible curverin the Galilean 3-space.We give relations between the Frenet apparatus and the curvatures ofrandrλ.Using these relations,we get some conclusions.Also,we investigate ruled surfaces generated via the curverλ.In the last section, there are examples, two of which are ruled surfaces.

2 Preliminaries

Let us consider a curveα(t)in 3-dimensional Euclidean space with{T,N,B}as the Frenet frame at the pointP=α(s)ofα(t).dis described as a vector tightly fastened to Frenet trihedron {T,N,B} such thatd=d1T+d2N+d3B, whered1,d2,d3are constant numbers andd21+d22+d23= 1.kis described as a line tightly fastened to Frenet trihedron{T,N,B}in the direction ofdand passing through pointP(see Fig.1)[12].LetPvdenote a point on the linekat a constant distancevfromP.During the movement of the Frenet trihedron along the curveα(t),Cv(t)is geometric place ofPv(s)which is defined as a curve at a constant distance from the edge of regression of the curveα(see Fig.1)[12].

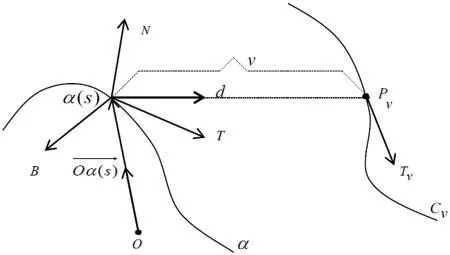
Figure 1:The curve α and the curve Cv

The Galilean space G3is one of the Cayley-Klein geometries with projective signature(0,0,+,+)as described in[6].The absolute of the Galilean geometry is an ordered triple{w,f,I}wherewis the ideal(absolute)plane,fis the(absolute)line inwandIis the fixed elliptic involution of points off.For more detailed information about this space,see[2,3,9,13,14].

Now,let us consider the basic definitions and notions.

The Galilean vector product of two vectors in G3is

Definition 2.1.An angleθbetween two unit non-isotropic vectors=(1,y,z)and=(1,y1,z1)in G3is described in[16]as

2.1 Curves in Galilean 3-Space

Letαbe a curve given byα:I→G3,α(t)=(x(t),y(t),z(t))wherex(t),y(t),z(t)∈G3.In this case ifx＇(t)/=0,α(t)is said to be a regular curve.

Letα:I→G3be a regular curve in G3.Arc length of the curveαisds= |x＇(t)dt| = |dx|.Hence,we obtains=x.Letα:I→G3be a curveα(x)=(x,y(x),z(x))then we say that the curve is parameterized by arc length[4].

In this case, the functionsy,z:I→R are said to be coordinate functions of the curve.Here,differentiatingα(x)=(x,y(x),z(x))with respect toxand using the norm definition,we obtain

Then,α(x)is a unit speed curve.Letα:I→G3,α(x)=(x,y(x),z(x))be a regular unit speed curve in G3.Differentiatingα(x),we have

The using Eq.(4),then the tangent vector ofαis defined as

If we take the derivation of Eq.(5),we get

And from Eqs.(5)and(7),we writeα＇(x).α＇＇(x)=0.Here,the normal vector of the curveαis the vector in the direction.Then,the unit normal vector is defined as

Using Eqs.(7)and(8),we write

As a consequence,the unit binormal vectorB(x)ofαis

and then the frame {T(x),N(x),B(x)} chosen in this way is called the Frenet-Serret frame for unit speed curves in the Galilean 3-space[5].

Proposition 2.1.The Frenet formulae of a unit speed curveα(x)in G3is given by

where

is the curvature ofαand

is the torsion ofα[17].

3 Curve at a Constant Distance from the Edge of Regression on a Curve in Galilean 3-Space

Definition 3.1.Suppose thatris a curve in Galilean 3-space and{T,N,B}is the Frenet frame at the pointP=r(s)ofr.LetPλbe a point at a constant distanceλfromP.During the movement of the Frenet trihedron along the curver,rλ=r+λdis geometric place ofPλ,where

such thatd21+d22+d23=1,d1,d2,d3∈R andd2=1,|d|=1.In this case,rλis called curve at a constant distance from the edge of regression ofr.

Now, let us construct the Frenet frame ofrλgenerated by both the non-isotropic vectordand isotropic vectordand examine its curvature properties.

Case 3.1.dis non-isotropic.In this case,d12=1.Let usd1=1,d2=d3=0.Then,we obtain

whered(s)=T(s).

Theorem 3.1.Ifr(s)is a curve with arc length parameters,then the arc length parameter of the curverλis alsos.

Proof.By differentiating Eq.(14)

If we take the norm of two sides of Eq.(15),we have

which completes the proof.

Proof.By differentiating Eq.(14)and using Eq.(11),we have

which gives us Eq.(16).If we take derivation of Eq.(21)according tos,we get

Using Eq.(22)in Eq.(12),then we get Eq.(19).From Eq.(9),we easily obtain the Eq.(17)and from Eq.(10),we get Eq.(18).Considering Eq.(13),we obtain Eq.(20).

In these calculations we used

Corollary 3.1.Let(r(s),rλ(s))be the curves pair given with arc lengthsin G3.If the curveris a circular helix,rλis also a circular helix.

Proof.We know that if the curvaturesκandτofrare constants,is also constan√t and thenris a circular helix.If we takeκandτas constants in Eqs.(19) and (20), we getandτλ=τ.

Case 3.2.dis isotropic.In this case,d22+d32=1 andd=d2N+d3B.Hence,we have

When the king saw how very young the prince looked, and that he was still drinking of the fountain of wonder, he said: O youth! leave aside this fancy which my daughter has conceived in the pride of her beauty

whereλ2=λd2andλ3=λd3.

Theorem 3.3.Ifr(s)is a curve with arc length parameters,then the arc length parameter of the curverλis alsos.

Proof.By differentiating Eq.(23),we have

If we take the norm of two sides of Eq.(24),we havewhich completes the proof.

Theorem 3.4.Let(r(s),rλ(s))be the curves pair given with arc lengthsin G3.If the Frenet vectors ofrandrλare {T,N,B} and {Tλ,Nλ,Bλ}, the curvatures areκ,τandκλ,τλ, respectively, then the following relations hold:

Proof.By differentiating Eq.(23) and using Eq.(11), we obtainr＇λ=T-λ3τN+λ2τBwhich gives Eq.(25).If we take second derivation ofrλaccording tosand use Eq.(11) again, we getB.In the light of this last equation,if we take into account Eq.(12)we have Eq.(28).From Eqs.(8)and(26)is obtained and Eq.(27)is found as a consequence of Eq.(10).Considering(13),the torsion ofrλis found as in Eq.(29).

In these calculations,we use

Corollary 3.2.Let(r(s),rλ(s))be the curve pair given with arc lengthsin G3.If the curveris circular helix,rλis also a circular helix.

Proof.If the curvatures ofrare constants,is constant andris a circular helix.Consideringκandτas constants in Eqs.(28)and(29),the curvatures ofrλareandτλ=τ,respectively.

4 Ruled Surfaces Generated by the Curve rλ

The ruled surfaces in G3are three types.Definitions of the ruled surfaces of typeA,B,Cand current studies can be viewed in[6,15,17-20].Our goal is to define the ruled surfaces usingrλas the base curve andr＇λas the director curve,and to see if they can be developed.Here,we take into account ruled surfaces of typeA.

4.1 Ruled Surface of Type A Generated by rλ(s)=r(s)+λT(s)

A ruled surface of typeAin G3by using non-isotropic vectorDcan be written as

whererλis defined as in Eq.(14) and the vectorDis tangent ofrλ.Besides, the curverλdefined a directrix that does not lie in Euclidean plane and non-isotropic vectorD(s)=Tλis generator.The associated orthonormal triple ofXA(s,v)is given by

where Frenet trihedron{Tλ,Nλ,Bλ}is the Frenet frame of the unit speed curverλ(s)in Galilean 3-space.From Eq.(31),we see that two orthonormal triple coincide.

Additionally,the parameter of distributionPXAofXA(s,v)is

We know that ifPXA=0,XA(s,v)is developable.Then,we can express the following theorem:

Theorem 4.1.Suppose that(r,rλ)is a unit speed curves pair in Galilean 3-space withrλ=r+λT,where {T,N,B} and {Tλ,Nλ,Bλ} are the Frenet frame ofrandrλ, respectively.Dis a non-isotropic vector tightly fastened to Frenet trihedron{Tλ,Nλ,Bλ}ofrλat the origin andXA(s,v)is the ruled surface of typeAgenerated byDandrλ.Then,XA(s,v)is a developable surface.

Proof.By taking derivative ofrλwith respect to s and by using Theorem 3.2,we obtain

If we takeD=Tλ,we getPXA=0 from Eq.(32).Thus,XA(s,v)is developable.

Now,we consider thatvis a constant in the ruled surfaceXA(s,v).Then,XA(s,v)=rλ(s)+vD(s)is the equation of parametric curverλvfor the pointsKvon the ruled surface.In this case,we have

whereTλvis tangent vector at a pointKvofrλvforv-constant.Ifκλis a non-zero constant,we deduce from Eq.(34)thatrλis a Bertrand curve.

Finally considering Eq.(1),the angleθbetween non-isotropic vectorsTλvandD,we calculate asθ=vκλ.

4.2 Ruled Surface of Type A Generated by rλ =r(s)+λ2N +λ3B

Similarly to Section 4.1,a ruled surface of typeAin G3by usingD=Tλcan be written as

where the curverλ(s)=r(s)+λ2N+λ3Bis directrix andD(s)=Tλ=T-λ3τN+λ2τBis generator.In this case,the associated orthonormal triple ofXA(s,v)is found as Eq.(31).

Thus,the following theorem can be written:

Theorem 4.2.Suppose that (r,rλ) is a unit speed curves pair in Galilean 3-space withrλ=r+λ2N+λ3B, where {T,N,B} and {Tλ,Nλ,Bλ} are Frenet frame ofrandrλ, respectively.Dis a nonisotropic vector tightly fastened to Frenet trihedron{Tλ,Nλ,Bλ}ofrλat the origin andXA(s,v)is the ruled surface of typeAgenerated byDandrλ.Then,XA(s,v)is a developable surface.

Proof.By taking derivative ofrλwith respect to s and by using Theorem 3.4,we have

We take asD=Tλ,so by a straightforward computation,the parameter of distribution forXA(s,v)is calculated as follows:

Hence,XA(s,v)is developable.

5 Applications

Example 5.1.Consider the curve given by the parametrization

The Frenet frame fields of the curve ofφ(σ)are[Fig.2]

T(σ)=(1,σsin(σ)+cos(σ),-σcos(σ)+sin(σ)),N(σ)=(0,cos(σ),sin(σ)),B(σ)=(0,-sin(σ),cos(σ)).

Considering Eq.(14),the curveφλ(σ)generated by non-isotropic vectordin G3is

φλ(σ)=φ(σ)+λT,

φλ(σ)=(1+σ,(1-σ)cos(σ)+(2+σ)sin(σ),(1-σ)sin(σ)-(2+σ)cos(σ))

forλ=1(see Fig.2).Ifdis isotropic vector,from Eq.(23)we have

forr=1,(see Fig.2).

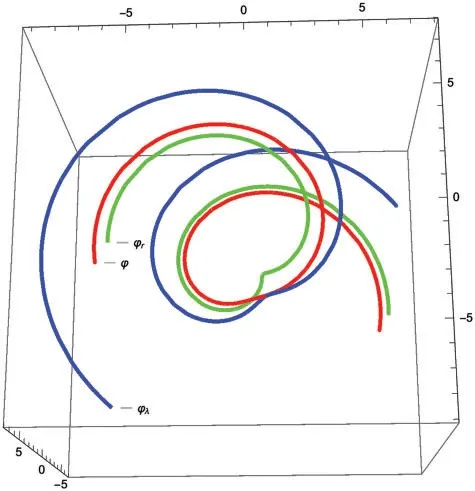
Figure 2:The red curve is φ(σ),the blue curve is φλ(σ)and the green curve is φr(σ)

Example 5.2.Let us consider the curve given by Eq.(38)in Example 5.1.The ruled surfaceXA(σ,v)obtained by using Eq.(38)in light Eq.(30)is

In Eq.(39),the curveφλ(σ)=(1+σ,(1-σ)cos(σ)+(2+σ)sin(σ),(1-σ)sin(σ)-(2+σ)cos(σ))is directrix and the non-isotropic vector

D(σ)=Tλ(s)=(1,σsin(σ)+(1+λκ)cos(σ),-σcos(σ)+(1+λκ)sin(σ))

is generator.Forκ=σandλ=1,Eq.(39)is shown in the Fig.3.

Example 5.3.Let us consider the curve given by Eq.(38)in Example 5.1.The ruled surfaceXA(σ,v)obtained by using Eq.(38)in light Eq.(35)is

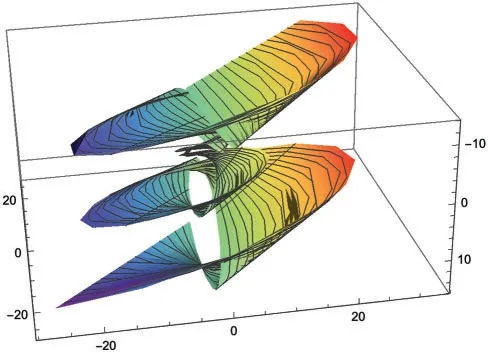
Figure 3:The surface XA(σ,v),for-π ≤σ ≤π,-1 ≤v ≤1

In Eq.(40),the curve

is directrix and the non-isotropic vector

Tλ(s)=(1,(σ-λ2τ)sin(σ)+(1-λ3τ)cos(σ),(1-λ3τ)sin(σ)+(-σ+λ2τ)cos(σ))

is generator.Forτ=1 andλ2=λ3=1,Eq.(40)is shown in the Fig.4.

Figure 4:The surface XA(σ,v),for-π ≤σ ≤π,-1 ≤v ≤1

6 Conclusion

In this study,we present a method that generates a new curve from the curve using the Frenet frame of a curve that is parameterized by arc length in G3.We show that it is possible in two ways to achieve this state in Galilean 3-space.We also calculate the Frenet frame and curvatures of the generated curve in terms of the Frenet frame and curvatures of the first curve.In this case,we reveal that if the first curve is helix,the generated curve is also the helix curve.In Section 4,for Case 3.1 and Case 3.2,ruled surfaces generated by the constructed curve and its tangents are discussed.It has been shown that the composed ruled surfaces are developable.

Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.