Modeling Drug Concentration in Blood through Caputo-Fabrizio and Caputo Fractional Derivatives

Muath Awadalla,Kinda Abuasbeh,Yves Yannick Yameni Noupoue and Mohammed S.Abdo

1Department of Mathematics and Statistics,College of Science,King Faisal University,Hafuf,Al Ahsa,31982,Saudi Arabia

2Institute of Statistics,Biostatistics and Actuarial Science,Faculty of Science,Universite Catholique de Louvain,Louvain-La-Neuve,1348,Belgium

3Department of Mathematics,Hodeidah University,Al-Hudaydah,3114,Yemen

ABSTRACT This study focuses on the dynamics of drug concentration in the blood.In general,the concentration level of a drug in the blood is evaluated by the mean of an ordinary and first-order differential equation.More precisely,it is solved through an initial value problem.We proposed a new modeling technique for studying drug concentration in blood dynamics.This technique is based on two fractional derivatives,namely,Caputo and Caputo-Fabrizio derivatives.We first provided comprehensive and detailed proof of the existence of at least one solution to the problem; we later proved the uniqueness of the existing solution.The proof was written using the Caputo-Fabrizio fractional derivative and some fixed-point techniques.Stability via the Ulam-Hyers(UH)technique was also investigated.The application of the proposed model on two real data sets revealed that the Caputo derivative was more suitable in this study.Indeed,for the first data set,the model based on the Caputo derivative yielded a Mean Squared Error(MSE)of 0.03095 with a corresponding best value of fractional order of derivative of 1.00360.Caputo-Fabrizio-basedderivative appeared to be the second-best method for the problem,with an MSE of 0.04324 for a corresponding best fractional derivative order of 0.43532.For the second experiment,Caputo derivative-based model still performed the best as it yielded an MSE of 0.04066,whereas the classical and the Caputo-Fabrizio methods were tied with the same MSE of 0.07299.Another interesting finding was that the MSE yielded by the Caputo-Fabrizio fractional derivative coincided with the MSE obtained from the classical approach.

KEYWORDS Pharmacokinetics;caputo fractional derivative;stability study;Caputo-Fabrizio fractional derivative

1 Introduction

Drugs are often inoculated in human blood during the treatment of a disease.One interesting fact is that the concentration of the drug decreases over time once it is inoculated.The initial concentration of a drug and many other parameters are used by medical practitioners to determine the frequency at which a specific drug should be administrated to reach the goal of curing a disease.

The clinical development of a new drug involves many phases.During phase 1 of drug development,the experimenter routinely evaluates time elapse until a new regimen reaches its steady state.The steady state here refers to the state at which the concentration of a drug in the blood does not change consistently anymore over time.In practice,patients have to take several shots of the drug in order to recover.However,each time a dose of the drug is administrated,part of it spreads all over the body and exists through excretions.The remaining part will accumulate to form sediment.The steady-state is reached when the concentration of the new dose coincides with the concentration of sediment.To identify the time from the first inoculation to the steady-state,the patient’s blood is sampled at regular time span intervals and the drug concentration is measured from the sample[1-5].

Many research works were produced in line with the evaluation of the steady-state of a drug in blood plasma.An overview of the selected method was proposed by Maganti et al.[6]and included approaches such as a Bayesian approach based on Markov Chain Monte Carlo (MCMC); Nostatistical-significance-of-trend(NOSTASOT;spline regression among others.In the same line,a non-Newtonian-based important factors approach was introduced by Johnston et al.[7].

Besides the few but consistent methods of evaluating the steady-state during phase I study are many other approaches that we believe can be used successfully.We think of Fractional Calculus(FC)in this regard.Indeed,over the past decades,many researchers have successfully applied FC to solve real-life problems.One can name a few of these successes just to mention.For instance, Reference[8]was a review of recent trends in the successful application of FC in Biology and medical sciences.Margin has shown in[9]that FC could be successfully used to describe the dynamic of the events that occur in human blood tissues.Toledo-Hernandez et al.[10] have produced a piece on fermentation process modeling using FC.Fatma et al.[11]have studied the spray of omicron SARS-CoV-2 variant of COVID-19.Naik et al.[12]have investigated the effect of prostitution on HIV transmission dynamics.Qureshi et al.[13]have studied the concentration of ethanol in blood using a fractional derivative.They are many such examples in which FC has been successfully applied in modeling real-life phenomena[14,15].The list is non-exhaustive however,we would recommend to a reader with an interest in the application of fractional calculus in Biology and Medicine to read the following selected papers(see[16-25]).

Almost eighty years ago,more precisely in the year 1940,the mathematician Ulam asked about the stability of functional equations[26],and a year later the mathematician Heyer responded to the question.By setting the necessary conditions for the stability of functional equations[27].This result was generalized to differential equations, and it was believed that Obloza was the first to make this generalization[28],after which Alsina and Ger published a scientific paper containing what is known today as the Hyers-Ulam stability[29],Rus investigated the Hyers-Ulam stability of differential and integral equations using the Gronwall lemma [30].Recently, the Hyers-Ulam stability problems of several differential equations were investigated by using the method of integral operators,see[31-34].

In this work, we kept a similar approach to earlier discussed examples.Indeed, we introduced modeling of the drug’s concentration blood using two fractional derivatives,namely the Caputo and the Caputo-Fabrizio fractional derivatives.Moreover,some qualitative analyses of the aforementioned models were obtained.

The remaining work is organized as follows.A review of FC definitions is provided in Section 2.The Section 3 focuses on a review of drug concentration modeling in blood.Section 4 establishes the existence and uniqueness of FC based approach proposed in this work.Section 5 establishes the Ulam-Hyers stability of the proposed fractional model.Section 6 is dedicated to applications on real-life data and the final section is the conclusion and discussion.

2 Some Useful Fractional Calculus Elements

FC has a strong foundation built upon definitions.Nowadays,they exit many fractional derivatives,each of them having its specific advantages and down points.This section focuses on some FC concepts required for the rest of the paper.

Definition 2.1[35,36].Givenτ ＞0, a positive real number, the one-parameter Mittag-Leffer function is defined as follows:

wherex∈R andΓstands for the commonly known gamma function,which is defined as follows:

This function was introduced by the author of the same name in 1903(see[37]).With the advent and spread of research in the field of FC, the function quickly became an essential tool for FC and particularly for fractional differential equations (FDE).In practice, most solutions of FDE are expressed in terms of the Mittag-Leffer function.

Another important derivative that is among the basis of FC is the Caputo fractional derivative.It is an integral form-based derivative defined as follows.

Definition 2.2[35].The Reimann-Liouville(RL)fractional integrals is defined by

Definition 2.3[35].The Caputo fractional derivative of orderνof a functionϑ: R+→ R is given by

where[ν]stands for the integer part of the real numberν.

Definition 2.4[35].Givenf,a function defined such that,φ∈H1(c,d),c ＞dandγ∈[0,1],then it is possible to define another form of the Caputo Fractional derivative.This form is often called the new Caputo fractional derivative,and it expressed as follows:

It is even possible to derive another useful fractional derivative that is used in this work.Indeed,if the functionfintroduced in Definition 2.3 is such thatφ /∈H1[c,d]then,the new fractional derivative called Caputo-Fabrizio fractional derivative is obtained as follows:

The Caputo-Fabrizio fractional integral exists and is also useful in solving FDE.The said integral is defined as follows:

Definition 2.5[35].Givenγ ＞0, a positive and real number denoting the order (fractional)of integral.The Caputo-Fabrizio fractional integral of a continuous functionf: [0,+∞)→R is defined by

whereMis a function with the propertyM(0)=M(1)=1.It is called the normalization function.

We end the shortlist of fractional derivatives and integrals of this section with Riemann-Liouville definitions.

Definition 2.6[35].Reimann-Liouville(RL)fractional integral is given by the following formula:

So far in this section,three fractional derivatives and two fractional integrals have been introduced.To end this section,we will state without proving some important Lemmas.These lemmas are used in sequel in the process of proving the existence of a solution to the problem and the uniqueness of the existing solution to the core problem which is also defined in the coming sections.

Lemma 2.3[38](Krasnoselskii’s Theorem).

Let us consider a Banach spaceB,and a convex setQsuch thatQ⊂B.Moreover,letq∈Q,and let us assume thatHcan be written asH=H1+H2.If in addition,is a bounded set inBsatisfying the following two conditions:

i)H1:→Bis continuous and completely continuous;

ii)H2:→Bis a contraction,a continuous non-decreasing functionω:[0,∞]→[0,∞],withω(q1)＞q1,q1＞0,such that|H2(q1)-H2(q2)|≤ω(||q1-q2||),for anyq1,q2∈.

Then it follows that:

1)H(q0)=q0,q0∈,or

2) ∃q∈∂Qandλ∈(0,1)withq=λH(q)+(1-λ)q.

Lemma 2.4[38].(Banach’s Contraction mapping principle).

LetXis a Banach space and let the operatorQ:X→Xbe a contraction.Then,Qadmits a unique fixed pointx∈XwithQx=x.

3 A Review of Literature on Modeling of Drug Concentration in Blood

This section provides an overview of pharmacokinetics theories and the classical approach to building the dynamic model.A common approach to overcoming disease is to provide the sick person appropriate drug that will target harmful germs.It is therefore very substantial to inoculate the appropriate dose of the drug at suitable time intervals.Phase I of the clinical study of any drug focus on determining these parameters.Pharmacokinetics is defined as the branch of medicine that studies the dynamic(kinetics)of the drug when it is inoculated in a living body.In phase I of a clinical study,blood samples are taken at a regular time interval to evaluate the drug concentration.This is a purely experimental approach.There also exists a theoretical approach that consists of using a mathematical model and some historical data to develop a predictive model.A model that would predict drug concentration levels in the blood over time.In general,interest among researchers in computational biology has increased significantly over the past decades.Juinn et al.have dedicated research [39]to the study of Pharmacokinetics and Metabolism during a drug development process.Absorption,distribution,metabolism,and elimination(ADME),Reference[40]was the set of processes through which a drug is utilized by an individual leading to a concentration decrease over time.

It was mentioned in an earlier section that drug concentration decreases over time.Hence, a suitable mathematical model to describe such a process can be an exponential decay model.The following differential equation describes the decrease observed over time.

whereμis a constant coefficient that is experimentally estimated.It is called theexponential decay constant.This constant varies from one drug to another.Let us consider that at the initial state, att=0 a patient has inoculated a doseC0,of a drug,then one can estimate the drug concentration level,Cin the patient’s blood at any timetby solving the differential equation, Eq.(1) (see [41]), and its solution is written as

This study aims to investigate the performance of fractional differential equations in modeling while comparing them with classical differential equations used for solving the same problem.In the next sections,Caputo’s derivative and Caputo-Fabrizio’s derivative are used to build a fractional counterpart of the differential equation Eq.(1).The said models are applied to real-life data sets and the error rates they produce are used for a comparative study.The corresponding counterpart of Eq.(1)based on Caputo’s derivative and Caputo-Fabrizio’s derivative are respectively defined as follows:

In order the simplify notation and for conformity purpose,let a kernel functionf:[a,T]×R →R be chosen as a continuous function and satisfyingf (0,CFC(0))= 0, then Eqs.(3) and (4) become respectively Eqs.(5)and(6)shown below:

The following Lemmas introduce more generalized formulae of the solutions to the fractional drug concentration models with the initial condition,as defined by Eqs.(5)and(6).

Lemma 3.1:(see [35]).Givenγ ＞0, and letnbe the integer part of the real numberγ.Let us consider the following initial value problem:

whereψ(i)(0)=ψ(i)0,i=0,1,...,n-1,and the functionφ∈C[0,T]is defined to be continuous.

There exists a solution to Eq.(7)and,the said solution can be written as follows:

wherewi(t)=J0ieγ(t),i=0,1,...,n-1,eγ(t)=Eγ(βtγ).

Remark: If the real numberγ, used in Lemma 3.1 is defined in a way that 0＜γ ＜1, then it follows that solution to Eq.(7)can fully be defined by the mean of Eqs.(8)-(9).In which case the said solution is denoted by

Using Lemma 3.1 the solution to Eq.(3), when the derivative is defined in Caputo sense is expressed as follow

Lemma 3.2(see[35]).Let 0＜γ ＜1,CF0C0∈R andσ∈C1[a,b]withσ(0)=0,then the following initial value problem

has a unique solution which is moreover expressed by the following expression:

withI1σ(t)representing the primitive function ofσ.Moreover,explicit form of the coefficients found in Eq.(13)are provided here and defined as

4 Existence Result for the Drug Concentration

Considering the initial value problem given by Eq.(6), and denoting byH=C([0,T],R)the Banach space of all functionsf, which are also selected or built such thatfis continuous from the closed interval[0,T]to R,moreover let the space be endowed with the norm defined as

Let an operatorE:H→Hbe defined as follows:

Eq.(15)is used to prove the existence and uniqueness of the solution.Besides,Lemmas 2.3 and 2.4 are needed in the process of proving the existence of a solution to the model proposed in Eq.(6).It is also used to prove the uniqueness of the solution found.

Theorem 4.1:Let us consider the functionf: [0,T]×R →R.Moreover, iffis a continuous function defined in a way that the following two assumptions hold:

i)∃k1＞0 such that

|f (t,CF C1)-f (t,CF C2)|≤k1|CFC1-CFC2|,∀t∈[0,T],

for allCFC1,CFC2∈R.

ii)|f (t,CFC)|≤y1(t),∀(t,CFC)∈[0,T]×R,

where,y1∈C([0,T],R+)with

Moreover,assume that the following inequality holds for the defined constant:

Based on above setting,one is sure of the existence of at least one solution to the problem Eq.(6),subject to its initial conditions.

Proof.Let us consider the close setBr={CFC∈H,||CFC||≤r}where the radius,ris such that

Let us introduce two operators,E1andE2which are built within the domain ofBrand explicitly defined as

Given two elementsCFC1,CFC2∈Br, then it follows:

henceE1CFC1+E2CFC2∈Br.

In the forthcoming step of the proof, we will show that the operatorE2is a contraction.Let us start by observing that ∀t∈[0,T],∀CFC1,CF C2∈Br, the following relation holds:

Eq.(19)is an evidence thatE2is a contraction.

Moreover,E1is a continuous operator due to the continuity ofCFC.On the other hand,E1is bounded uniformly,since

Beside all the above properties,one can prove compactness ofE1in the following approach:

Fort1,t2∈[0,T],such that(t1＜t2),it follows that:

The quantity defined on the right-hand side of the inequality Eq.(20) goes to zero ast1→t2.Moreover,it is observed that the quantity||(E1CFC)(t2)-(E1CFC)(t1)||does not depend onCFC,this implies thatE1is relatively compact.A Recall of Lemma 2.2 is enough to derive the conclusion thatE1is a compact operator on the closed setBr.Moreover,recalling Lemma 2.3,is enough to conclude on the existence of a solution to Eq.(6).Q.E.D.

Theorem 4.2:Letf:[0,T]×R →R be a continuous and assume moreover that

then the solution to the initial value problem Eq.(6)is unique.

Proof.Consider the close setBr={CFC∈H,||CFC||≤r}with

On the other hand,the following inequality is derived from the quantity or norm of|f (t,C(t))|:

Using Eqs.(21)-(22)leads to the following relation:

Eq.(23)implies thatECFC∈Br,∀CFC∈Brwhich means that in generalEBr⊂Br.

The second step of this proof is to show that the operatorEis a contraction.To do so,observe that ∀CFC1,CFC2∈H,the following relation holds:

The relation given by Eq.(24)leads to

On can see from Eq.(25) thatEis a contraction.Therefore, recalling Lemma 2.4 is enough to conclude that Eq.(6) has a unique in the closed interval [0,T].The said solution is built subject to initial values problem conditions.Q.E.D.

Having proven the existence and the uniqueness of a solution to the problem defined by Eq.(6),we finally summarize the analytical solutions(see[34])for these fractional models as follows:Based on Lemma 3.1,the analytical solution for the drug concentration model via Caputo sense Eq.(5)is given by

Based on Lemma 3.2, the analytical solution for the drug concentration model via Caputo-Fabrizio sense Eq.(6)is given by

All the necessary theoretical work on the proposed approach was done in previous sections.In the next section stability of the model is studied.

5 Ulam-Hyers Stability Results

In this section,we discuss the UH and generalized UH(GUH)stability of the considered problem.

Definition 5.1.Letf: [0,T]×R →R be continuous.Then Eq.(6) is UH stable if there existsκf ＞0 andε ＞0 such that each solutionCFN∈Hof

there exists a solutionC∈Hof Eq.(6)with

Definition 5.2.Letf:[0,T]×R →R be continuous.Then Eq.(6)is GUH stable with respect toΛf∈C(R+,R+)withΛf(0)=0,forε ＞0 such that each solutionCFN∈Hof Eq.(28),there exists a solutionCFC∈Hof Eq.(6)with

Remark 5.3.CFN∈Hsatisfies Eq.(28)if and only if there exists a functionη∈Hwith

Lemma 5.4(Gronwall’s Lemma,[42]).LetT＞0,andd＞0.Assume thatω,ϖ: [0,T] →R+are continuous.If

By Remark 5.3,the solution of Eq.(31)can be formulated by

Hence,we will make the following remark.

Remark 5.5.LetCFN∈Hsatisfies Eq.(28).ThenCFNis a solution to the next integral inequality:

Now we are ready to announce the results of the stabilization results for UH and GUH.

Theorem 5.6.Under the hypotheses of Theorem 4.1.Ifaαk1＜1, then the solution of Eq.(6) is HU stable on[0,T]and consequently GUH stable.

Proof.LetCFN∈Hbe a solution of Eq.(28).From Lemma(3.2),

has the unique solution

SinceCFC(0)=CF N(0),thenC0=N0.Hence Eq.(34)becomes

Thus,by our assumptions,Remark 5.5,along with Eqs.(32)and(35),we obtain

Asaαk1＜1,then

From Lemma 5.4,we have

which implies

|CFN(t)-CF C(t)|≤κfε,∀t∈[0,T].

Hence,Eq.(36)is UH stable inH.Moreover,if we setΛf(ε)=κfε,which satisfiesΛf(0)= 0,it is also concluded that Eq.(6)is GUH stable.

Let us consider the following CF-problem:

and the CF-inequality

For anyt∈[0,3],CFC∈R,

Therefore,i)and ii)hold.Also,From Theorem 4.1,Eq.(36)has a unique solution on[0,3].

LetCFN∈C([0,3],R)be a solution of Eq.(37).Then

From Theorem 4.1,we known(s1)withCFC(0)=C0has the unique solution

Hence,problem Eq.(36)is UH stable.If we set,we getΛf(0)= 0,which implies that problem Eq.(36)is GUH stable.

6 Applications on Real-Life Data

In this section,Caputo and Caputo-Fabrizio fractional derivatives are used to solve FDE for drug concentration modeling in blood.The next figure represents the so-called ADME process.It shows that drugs can be administrated through an oral or intravenous route.In this section,our experiments are carried out on the intravenous administration.Bold and red arrows are meant to highlight the paths considered in the study.The figure also shows where blood can be sampled to measure drug concentration at any time.It is important to mention that the oral route administration is not studied here because it falls apart in a completely different category of differential equations.

The following two experiments were designed with respect to Fig.1.In the experiments solutions based on the classical approach,caputo and Caputo-Fabrizio approaches are used to fit the data sets.Comparisons are made to select the best-performing method.

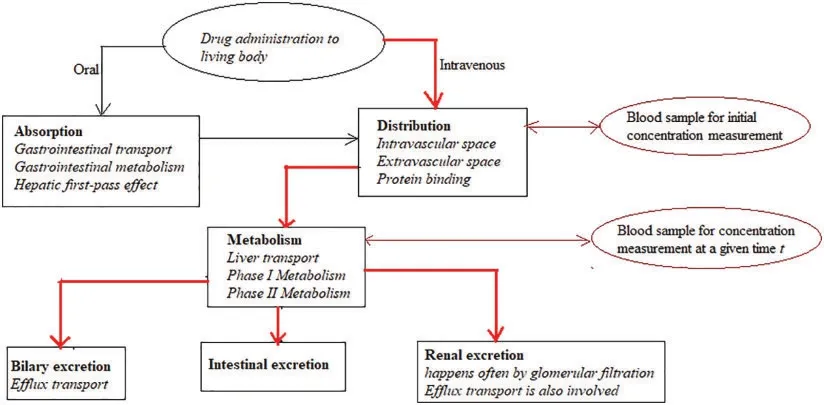
Figure 1:ADME process,with a highlight on intravenous route

Experiment N°1:

David Bourne(see[43])recorded experimental data on drug concentration behavior over time.In the said experiment a drug(antibiotic)was inoculated to a 50 kg woman through intravenous injection.For 10 h,blood samples were taken,and their drug concentrations were measured.The recorded data set was used to fit models defined by Eqs.(3)and(4).Their best parameters as well as their error level are given in the table below.

Table 1 contains values of the parameters for each model.Recalling classical model; Caputo derivative-based model;Caputo-Fabrizio based model described by Eqs.(1),(3)and(4),respectively.Looking at the MSE(see[36])of each model,Caputo derivative-based model has the best performance,withMSE=0.03095,andα=1.00360.The latest value is evidence that the error is minimized when the fractional order of the derivative doesn’t coincide with the first-order classical derivative.The Classical method and the Caputo-Fabrizio both occur as a second-best model with the sameMSE=0.04324.

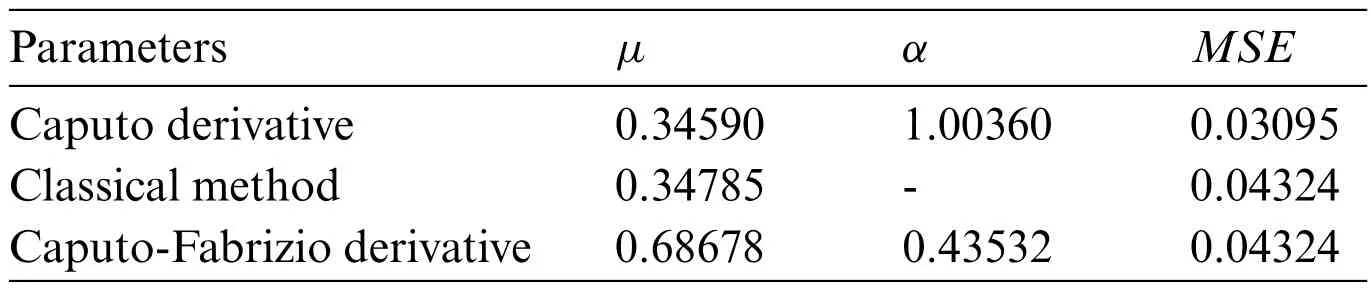
Table 1: Best parameters and MSE of Experiment N°1

Note:Best parameters were obtained through optimization routine,in particular error minimization.The non-linear optimization routine,nlmfrom R-programming was used for the purpose.μandαvalues from the tables are the combinations that lead to the lowestMSE.

Fig.2 shows the original data points and the fitted curves obtained from the classical method and the Caputo method.Curves overlap each other,this is also illustrated by the MSE range,which is very small.It is however possible to observe a little split of both curves from the 6thhour on the x-axis but zoom out the page containing the figure.

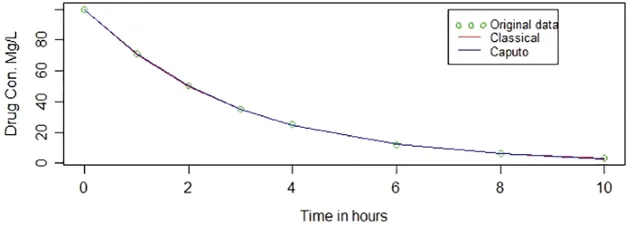
Figure 2:Caputo and classical methods

Fig.3 represents original data points alongside the fitted lines obtained through the classical method and Caputo-Fabrizio method.Both curves overlap each other all over the way.It is not surprising as both approaches have the sameMSE.

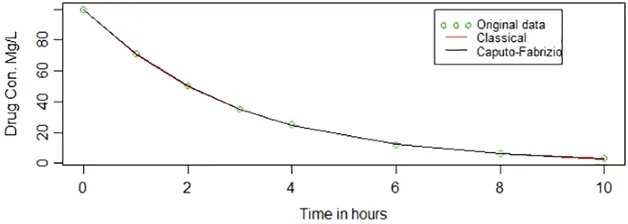
Figure 3:Caputo-Fabrizio and classical methods

Experiment N°2:

In this study,a newly developed drug was injected(Intravenous route)into a 50 kg female patient at a proportion of 20 mg/kg.Blood samples were taken on a regular basis and,the plasma was analyzed to determine the current drug concentration in the blood.The entire process generated a data set that was fitted by the mean of FDE based on Caputo and Caputo-Fabrizio derivative,defined by Eqs.(3)and(4),respectively.The data set was retrieved from[44].Performances of the models involved in the study are consigned below.

Table 2 contains values of the parameters for each model.Recalling classical model; Caputo derivative-based model;Caputo-Fabrizio based model described by Eqs.(1),(3)and(4),respectively.Looking at the MSE(see[36])of each model,Caputo derivative-based model has the best performance,with MSE=0.20992,andα=1.22335.The Classical method and the Caputo-Fabrizio both occur as a second-best model with the same MSE=0.63265.

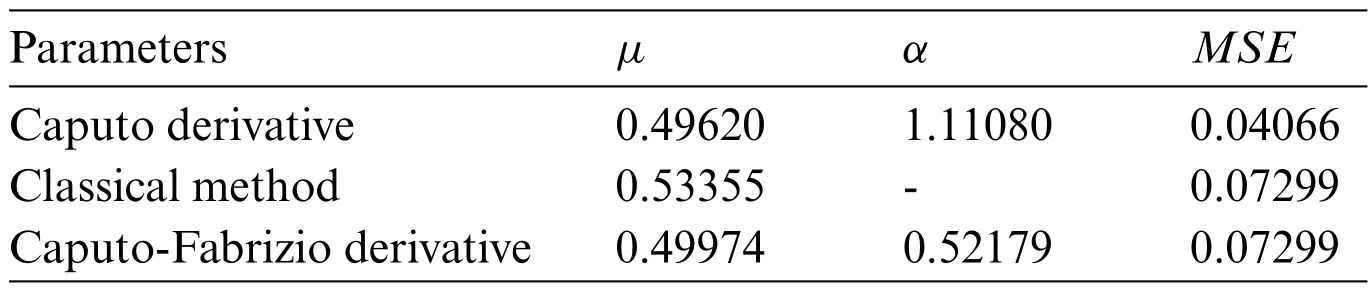
Table 2: Best parameters and MSE

Fig.4 shows the original data points and the fitted curves obtained from the classical method and the Caputo method.Although there are only a few data points,it is observed that the Caputo fitting line is closer to the original data points than the classical fitting line.

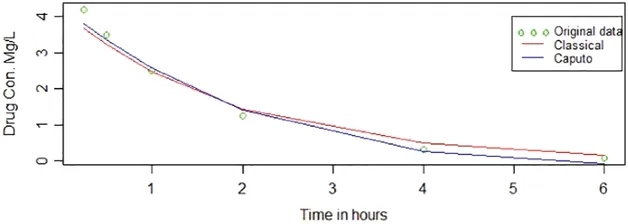
Figure 4:Caputo and classical methods from second experiment

Fig.5 represents original data points alongside the fitted lines obtained through the classical method and Caputo-Fabrizio method.

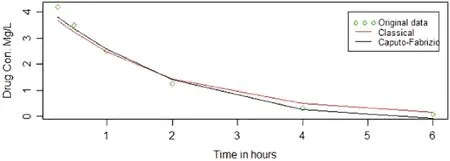
Figure 5:Caputo-Fabrizio and classical methods from second experiment

7 Conclusion and Discussion

The goal of this work is achieved.We have proven that fractional differential equations could be efficiently used for drug concentration modeling.In this regard, we have proven the existence and uniqueness of the solution based on some fixed point techniques.We have also provided a stability analysis in the Ulam-Hyers sense of the CF-type FDE model.Moreover,based on the results from the two experiments,it is observed that the Caputo derivative performs the best.On the other hand,the Caputo-Fabrizio and classical methods have the sameMSE.Based on the results of the experiments,one can observe that they are modeling problems for which the fractional calculus approach does not perform better than the classical method.Indeed, results from both experiments show that the Caputo derivative-based model has the best performance whereas Caputo-Fabrizio derivative-based model and the classical approach have the same performance(MSE).Moreover,they are the second best models.

In this study,every fractional order of derivative that leads to the lowestMSEfulfills the conditionα∈(0,1)U(1,2).The said condition is required when solving an FDE whose classical counterpart is solved by a first-order differential equation.

In future work, we aim to build a comprehensive framework for choosing the right fractional derivative for a given problem.

In practice, the outcome of this study can increase the accuracy of a new model’s parameters calibration.Indeed, if a new drug is developed, and if its concentration level in the blood (during phase IV)decreases over time following an exponential decay trend;then an FDE based on the Caputo derivative would be recommended for estimating the best parameters.The statementbest parametersrefer to theexponential decay constant,μand thefractional order of derivative,α,which would lead to the minimumMSE.

Authors’ Contributions:All authors contributed equally and significantly to this paper.All authors read and approved the final manuscript.

Acknowledgement:The authors express their thanks to the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia, for supporting this work through the Annual Funding Track by[Project No.AN000273].

Data Availability Statement:The data set used in the study is freely available through the https://www.boomer.org/c/p4/c02/c0208.php,it is found at[43].https://www.intechopen.com/chapters/49459 found at[44].

Funding Statement:This work was supported through the Annual Funding Track by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University,Saudi Arabia[Project No.AN000273],granted after a successful application by M.A.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.