A Note on Bell-Based Bernoulli and Euler Polynomials of Complex Variable
N.Alam,W.A.Khan,S.Obeidat,G.Muhiuddin,N.S.Diab,H.N.Zaidi,A.Altaleb and L.Bachioua
1Department of Basic Sciences,Deanship of Preparatory Year,University of Ha’il,Ha’il,2440,Saudi Arabia
2Department of Mathematics and Natural Sciences,Prince Mohammad Bin Fahd University,Al Khobar,31952,Saudi Arabia
3Department of Mathematics,Faculty of Science,University of Tabuk,Tabuk,71491,Saudi Arabia
ABSTRACT In this article, we construct the generating functions for new families of special polynomials including two parametric kinds of Bell-based Bernoulli and Euler polynomials.Some fundamental properties of these functions are given.By using these generating functions and some identities,relations among trigonometric functions and two parametric kinds of Bell-based Bernoulli and Euler polynomials,Stirling numbers are presented.Computational formulae for these polynomials are obtained.Applying a partial derivative operator to these generating functions,some derivative formulae and finite combinatorial sums involving the aforementioned polynomials and numbers are also obtained.In addition,some remarks and observations on these polynomials are given.
KEYWORDS Bernoulli polynomials;euler polynomials;bell polynomials;stirling numbers
1 Introduction
Special polynomials and numbers possess much importance in multifarious areas of sciences such as physics,mathematics,applied sciences,engineering and other related research fields covering differential equations,number theory,functional analysis,quantum mechanics,mathematical analysis,mathematical physics and so on (see [1–22]) and see also each of the references cited therein.For example, Bernoulli polynomials and numbers are closely related to the Riemann zeta function,which possesses a connection with the distribution of prime numbers.Some of the most significant polynomials in the theory of special polynomials are the Bell,Euler,Bernoulli,Hermite,and Genocchi polynomials.Recently,the aforesaid polynomials and their diverse generalizations have been densely considered and investigated by many physicists and mathematicians (see [1–18,22]) and see also the references cited therein (see [6–9,14–17]).The class of Appell polynomial sequence is one of the significant classes of polynomials sequence [1].In applied mathematics, theoretical physics,approximation theory,and several other mathematics branches.The set of Appell polynomial sequence is closed under the operation of umbral composition of polynomial sequences.The Appell polynomial sequence can be given by the following generating function:
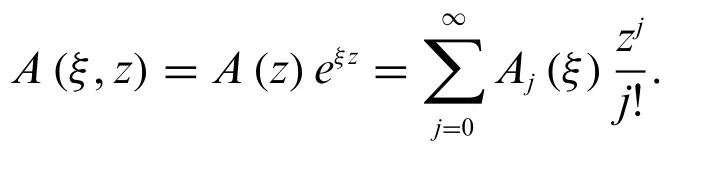
The power seriesA(z)given by
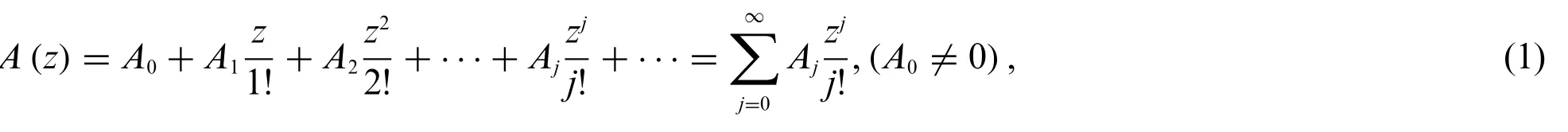
whereAi{i=1,2,3,···}are real coffiecients.It is easy to see that for anyA(z),the derivative ofA(z)satisfies
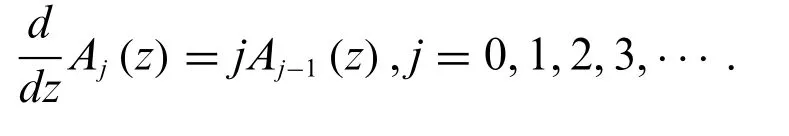
The Bell-based Bernoulli and Bell-based Bernoulli polynomials of the first kind are the special cases of Appell polynomials(see[2,18]).
The generalized Bernoulli and Euler polynomials of orderαare defined by(see[2–5])

and

respectively.
At the pointξ= 0,=(0)andare the Bernoulli and Euler numbers of orderα.
Forj≥0,Stirling numbers of the first kind are defined by

where(ξ)0=1,and(ξ)j=ξ(ξ-1)···(ξ-j+1),(ξ≥1).From(4),we see that

The Stirling numbers of the second kind are defined by

By(5),we note that

The generating function of Bell polynomialsBelj(ξ)are defined by(see[7])

In the special caseξ= 1,Belj=Belj(1),(j≥0)are the Bell numbers.From (1.7) and (1.8),we have

Recently, Duran et al.[2] introduced the generalized Bell-based Bernoulli polynomials are defined by

At the pointξ=η=1,Bel=Bel(1;1)are the generalized Bell-based Bernoulli numbers.
Kim et al.[13]and Jamei et al.[4,5]introduced the Bernoulli and Euler polynomials of complex variable are defined by
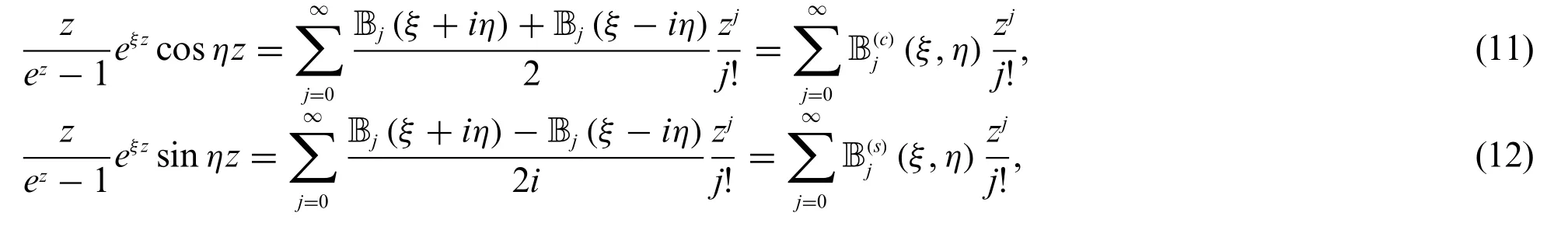
and

respectively.
Also they have prove that(see[4,5,8,9,19,20,21])

and

where

and

Motivated by the importance and potential applications in certain problems in number theory,combinatorics, classical and numerical analysis and physics, several families of Bernoulli and Euler polynomials and special polynomials have been recently studied by many authors, see [8,9,19–21].Recently, Kim et al.[13,16] have introduced the degenerate Bernoulli and degenerate Euler polynomials of a complex variable.By separating the real and imaginary parts, they introduced the parametric kinds of these degenerate polynomials.The manuscript of this paper is arranged as follows.In Section 2, we introduce parametric kinds of Bell-based Bernoulli polynomials and prove several identities of Bell-based Bernoulli polynomials by using different analytical means and applying generating functions.In Section 3,we establish parametric kinds of Bell-based Euler polynomials and investigate some identities of these polynomials.
2 Bell-Based Bernoulli Polynomials of Complex Variable
In this section,we consider the Bell-based Bernoulli polynomials of complex variable and deduce some identities of these polynomials.First,we present the following definition as

On the other hand,we suppose that

Thus,by(19)and(20),we have

and
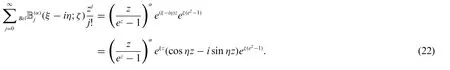
From(21)and(22),we get
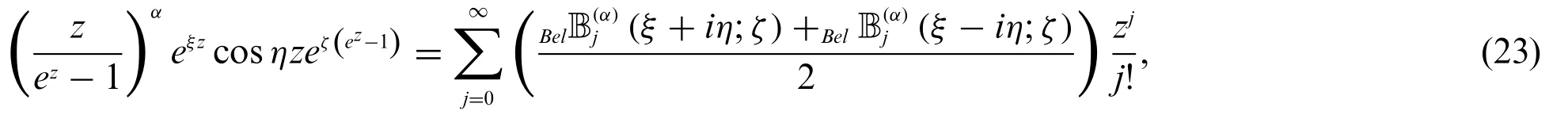
and
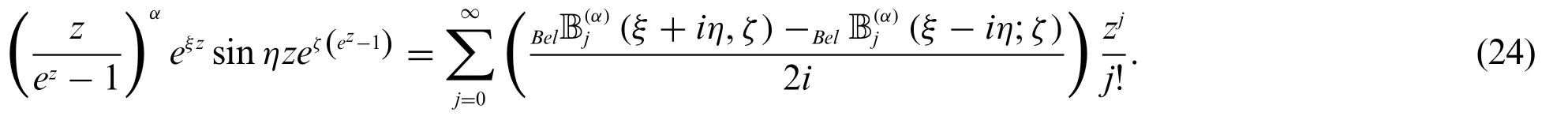

respectively.
Note thatBel(ξ,0;0)=(ξ),0,0;0)=0,(j≥0).
From(23)–(26),we have
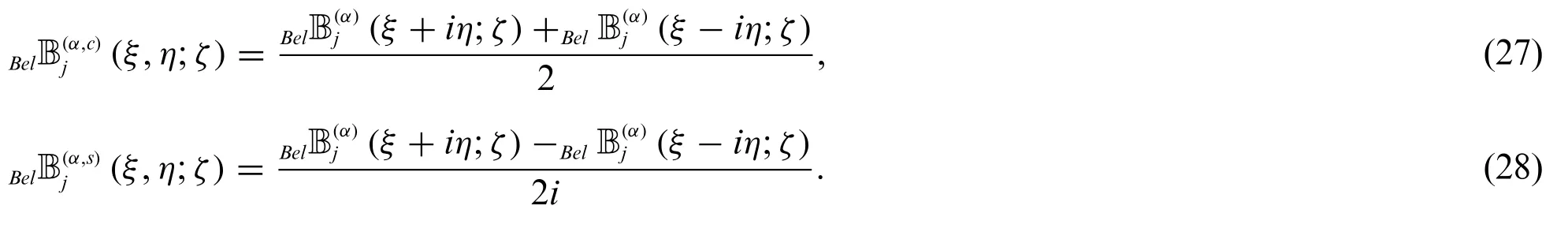
Remark 2.1.Forξ=ζ=0 in(25)and(26),we get

and

respectively.
It is clear that
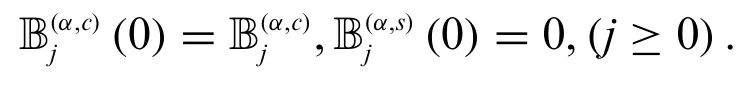
Remark 2.2.Lettingζ=0 in(25)and(26),we obtain

and

respectively.
Remark 2.3.On settingξ=0 in(25)and(26),we acquire

and

respectively.
Now,we start some basic properties of these polynomials.
Theorem 2.1.Letj≥0.Then

and
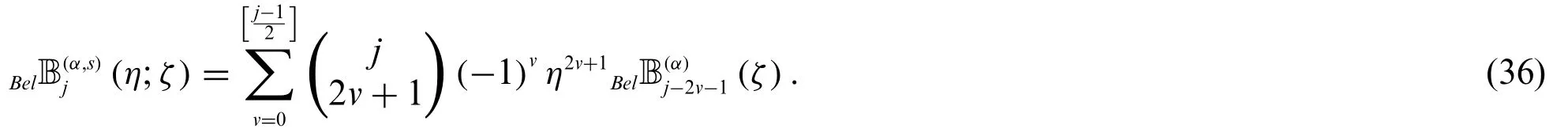
Proof.By(33)and(34),we can derive the following equations:
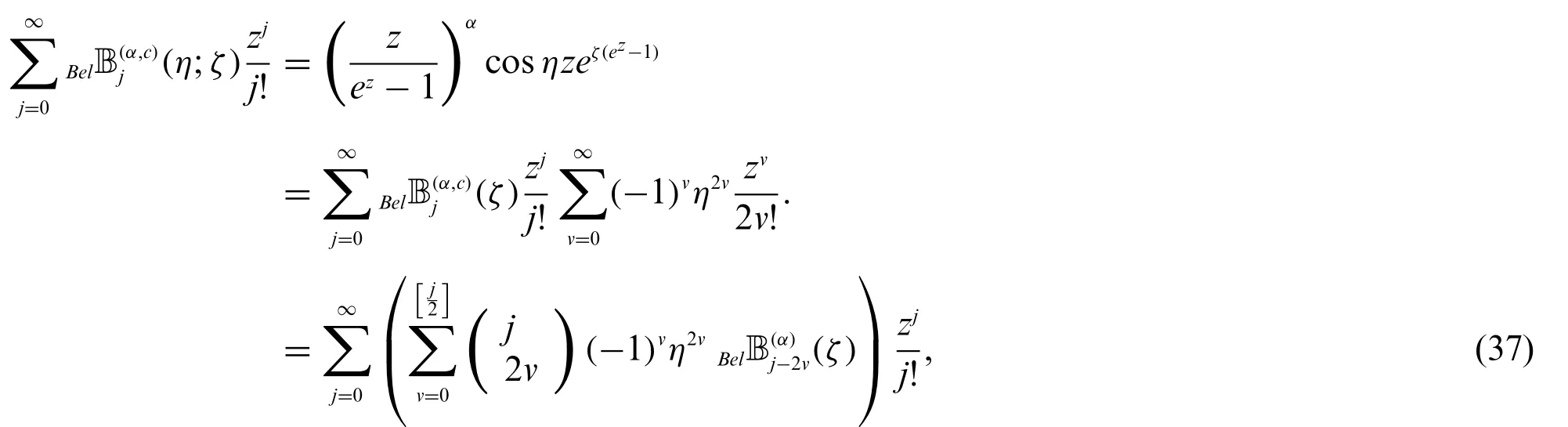
and
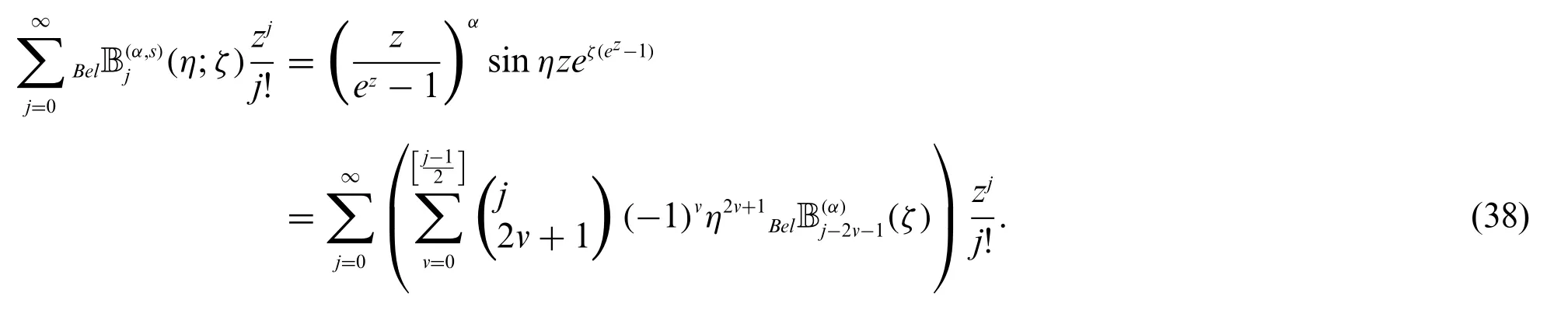
Therefore,by(37)and(38),we get(35).Similarly,we can easily obtain(36).
Theorem 2.2.Letj≥0.Then
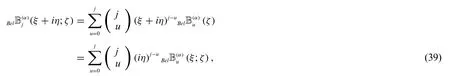
and
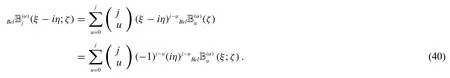
Proof.By using(21)and(22),we obtain(39)and(40).So we omit the proof.
Theorem 2.3.Letj≥0.Then

and

Proof.Consider
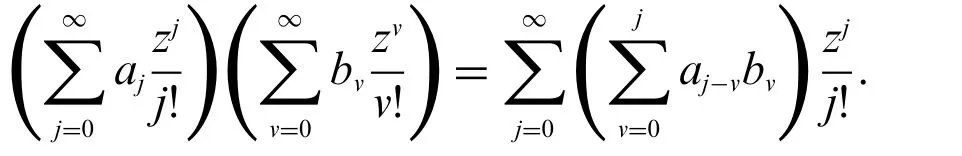
Now
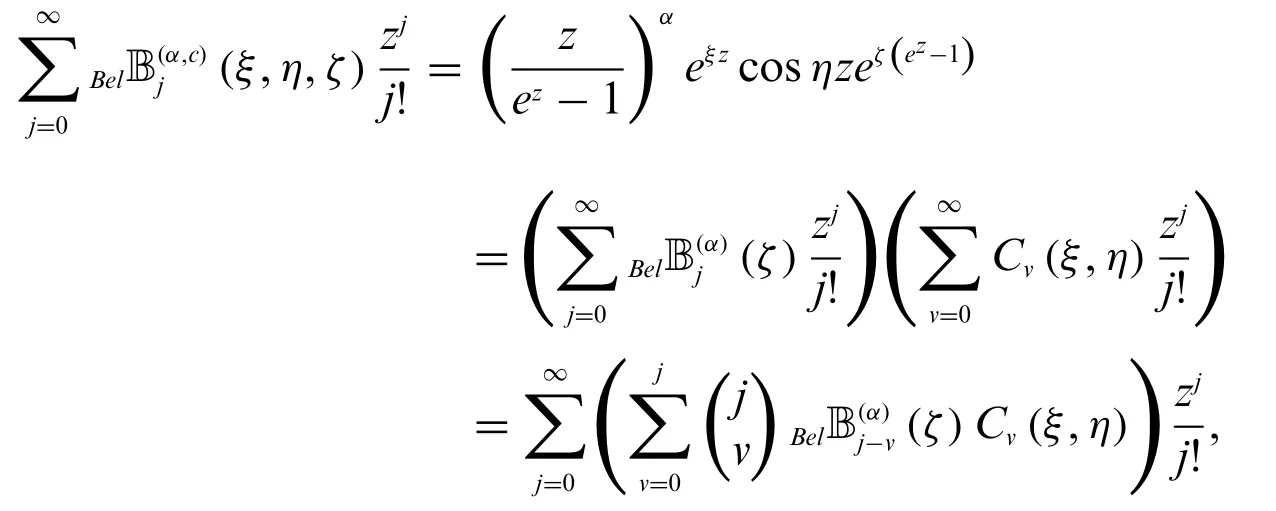
which proves(41).The proof of(42)is similar.
Theorem 2.4.For everyj∈Z+,we have

Proof.Using(25)and(26),we obtain(43)–(46).Here,we omit the proof of the theorem.
Theorem 2.5.Letj≥0.Then
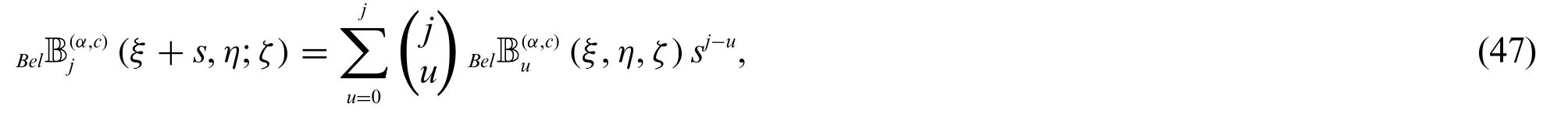
and

Proof.By changingξwithξ+sin(25),we have

which complete the proof(47).The result(48)can be similarly proved.
Theorem 2.6.Letj≥1.Then

and

Proof.Eq.(25)yields
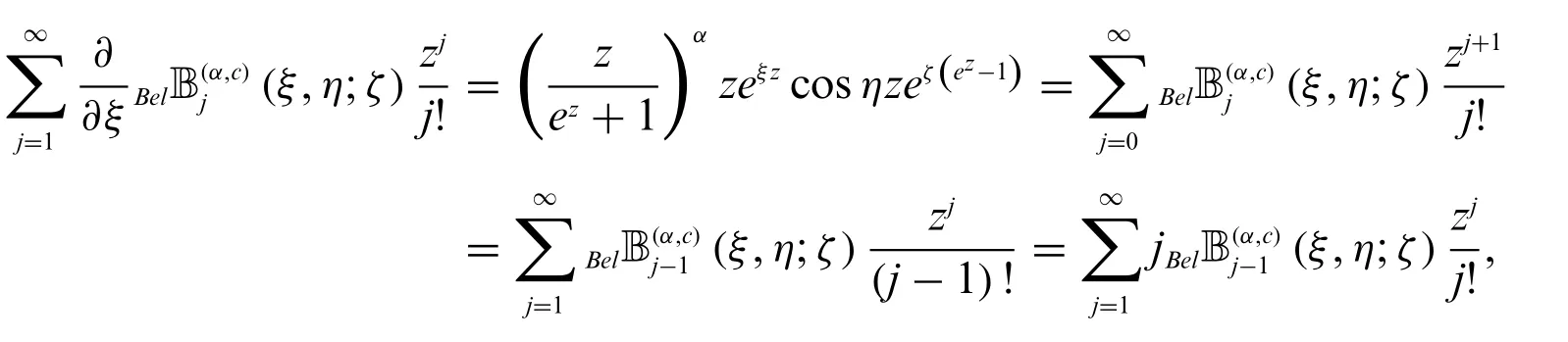
proving(49).Other(50),(51)and(52)can be similarly derived.
Theorem 2.7.Letj≥1.Then

and

Proof.By(25),we have

The complete proof of(53).The proof of(54)is similar.
Theorem 2.8.Forj≥0.Then

and
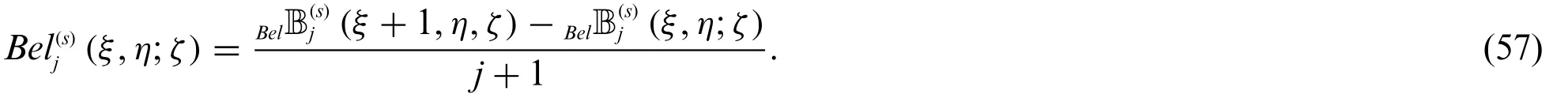
Proof.By(25),we have
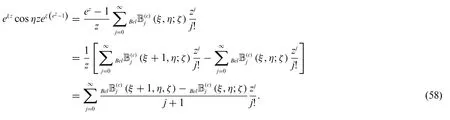
On the other hand,we have

In view of(58)and(59),we get(56).Similarly,we can easily obtain(57).
Theorem 2.9.Letj≥0.Then
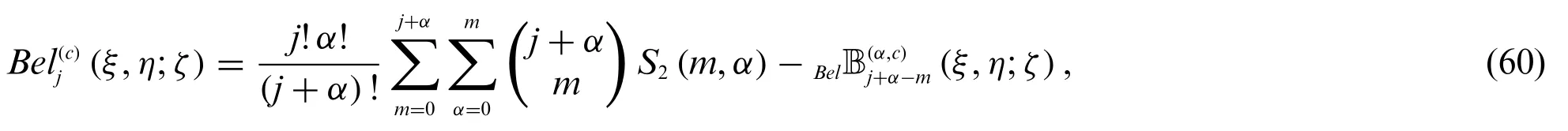
and
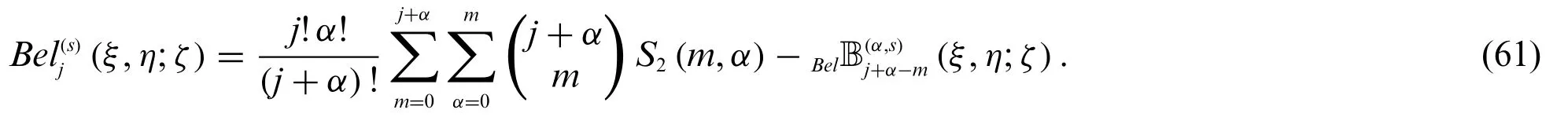
Proof.In definition 2.1,we have
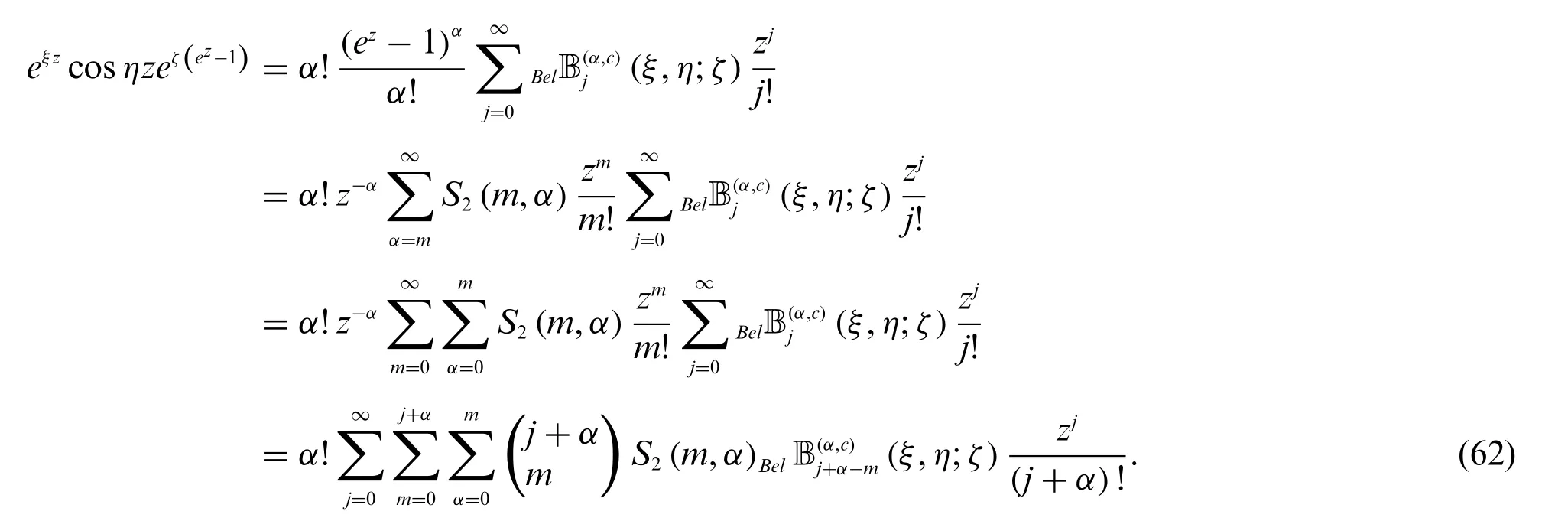
On the other hand,we have

Therefore,by(62)and(63),we obtain(60).Similarly,we can easily obtain(61).
Theorem 2.10.Letj≥0.Then
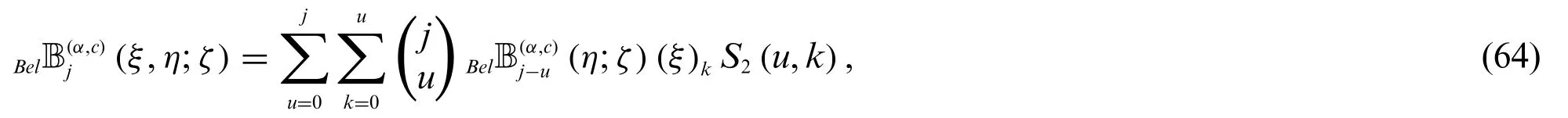
and
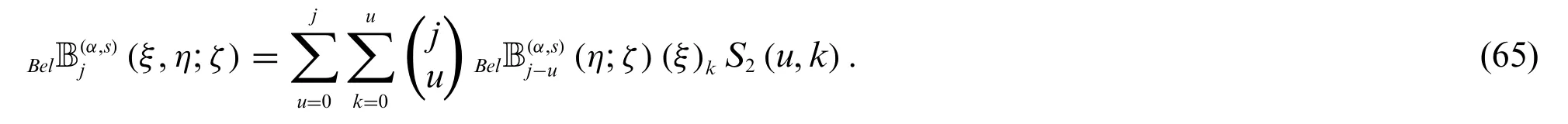
Proof.Using(7)and(25),we find
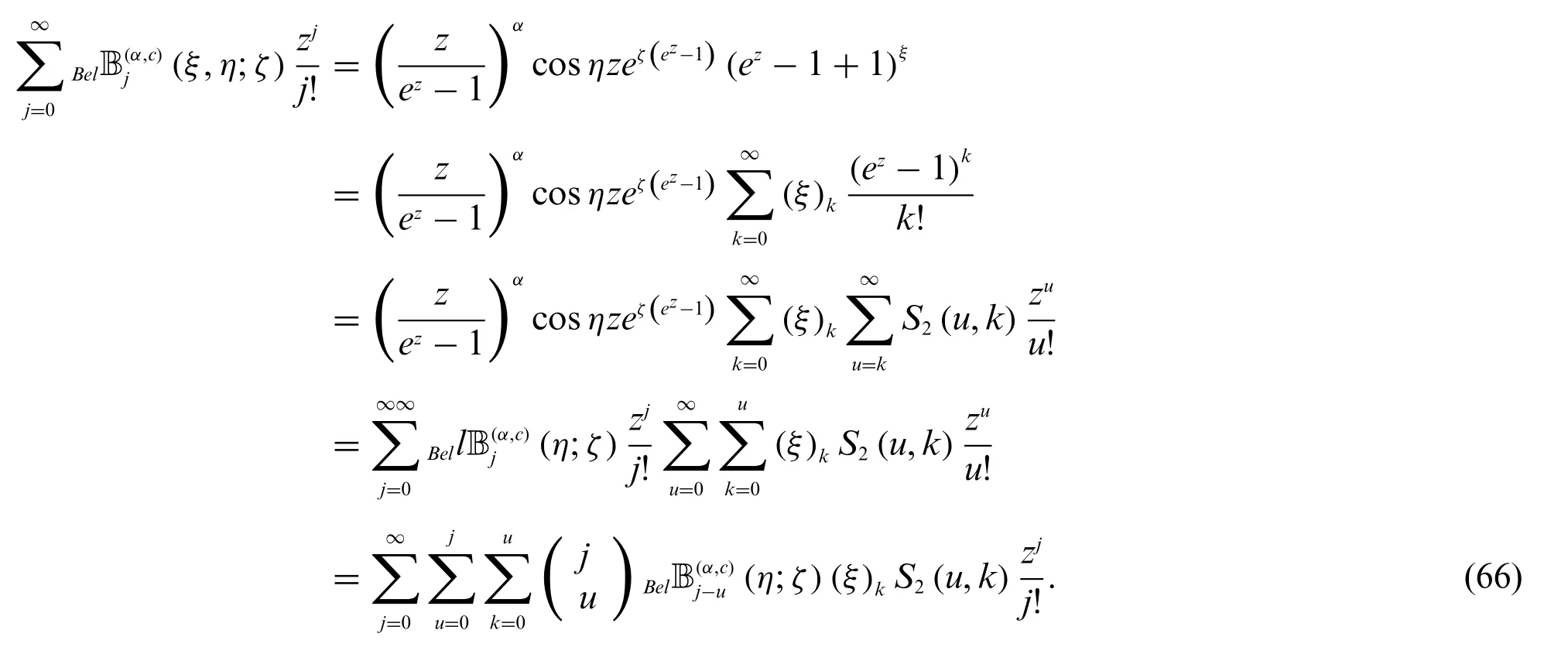
In view of(25)and(66),we get(64).Similarly,we can easily obtain(65).
3 Bell-Based Euler Polynomials of Complex Variable
In this section, we define Bell-based Euler polynomials of complex variable and derive some explicit expressions of these polynomials.Now we start with the following definition as
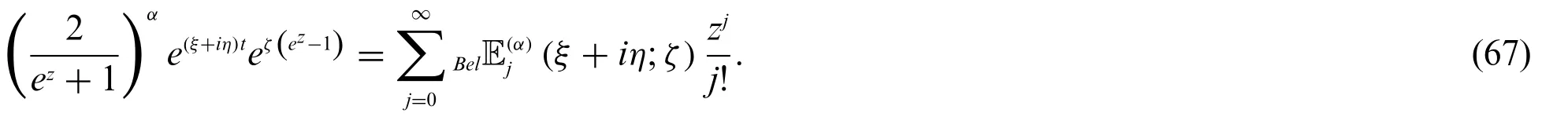
By using(67)and(20),we have

and

From(68)and(69),we get
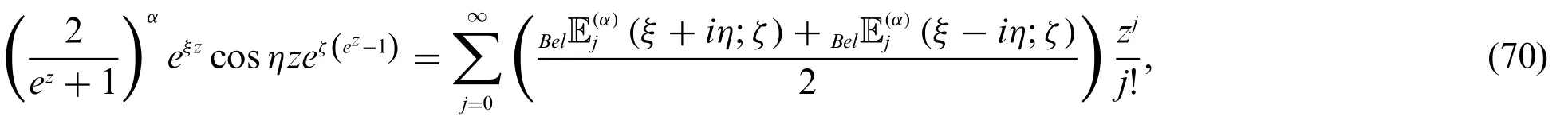
and

Definition 3.1.Letj≥0.We define two parametric kinds of cosine Bell-based Euler polynomialsBel(ξ,η;ζ)and sine Bell-based Euler polynomialsBel(ξ,η;ζ), for non negative integerjare defined by
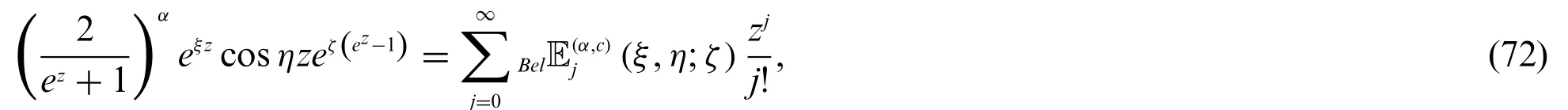
and
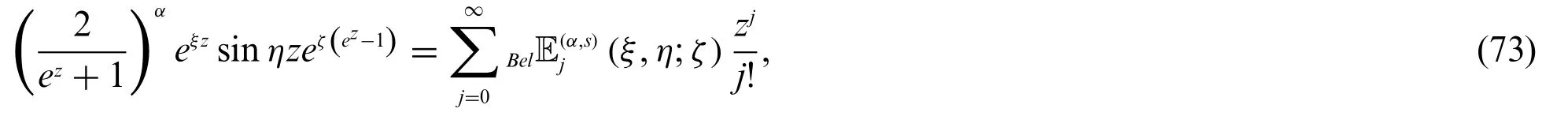
respectively.
From(70)–(73),we have
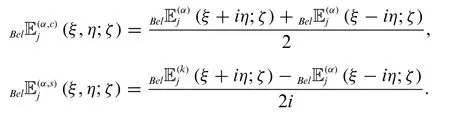
Note that
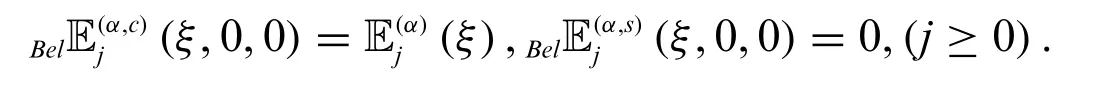
Remark 3.1.Forξ=0 in(72)and(73),we get

and

respectively.
Remark 3.2.Lettingζ=0 in(72)and(73),we obtain

and

respectively.
Remark 3.3.On takingξ=ζ=0 in(72)and(73),we acquire

and

respectively.
Theorem 3.1.Letj≥0.Then

and
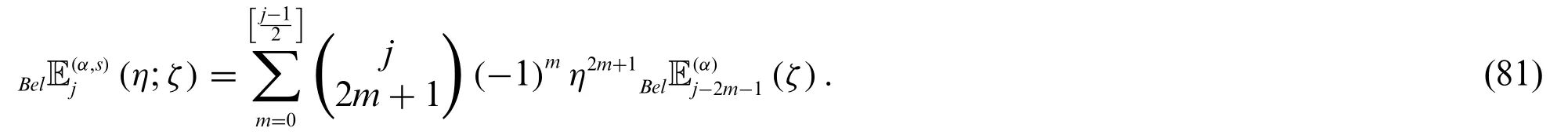
Proof.From(78)and(79),we can derive the following equations:
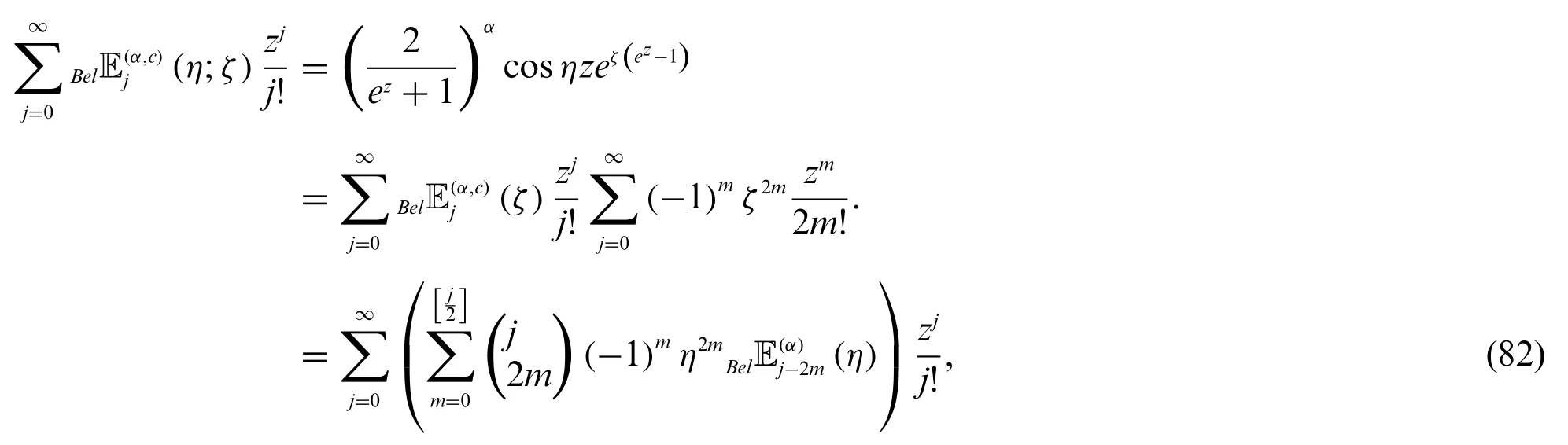
and
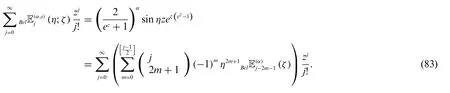
Therefore,by(82)and(83),we get(80).Similarly,we can easily obtain(81).
Theorem 3.2.Letj≥0.Then
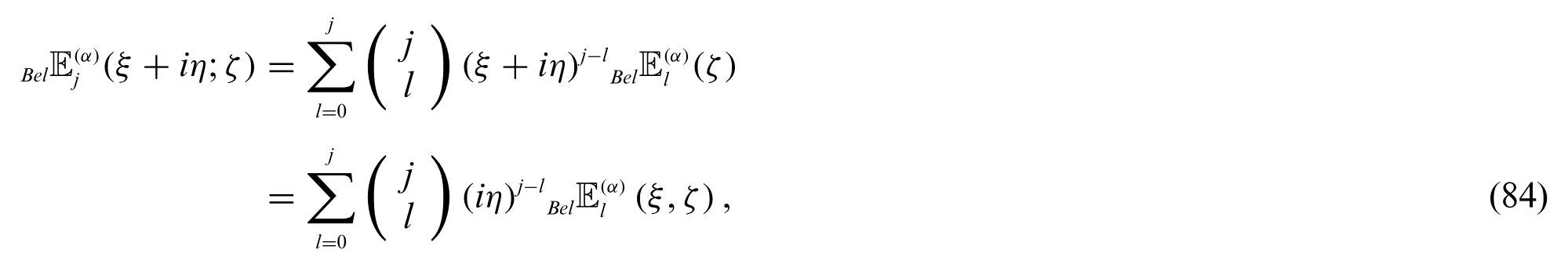
and
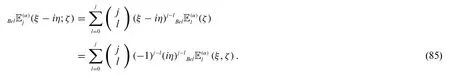
Proof.By using(68)and(69),we can easily get(84)and(85).So we omit the proof.
Theorem 3.3.Letj≥0.Then

and

Proof.Consider the identity,we have
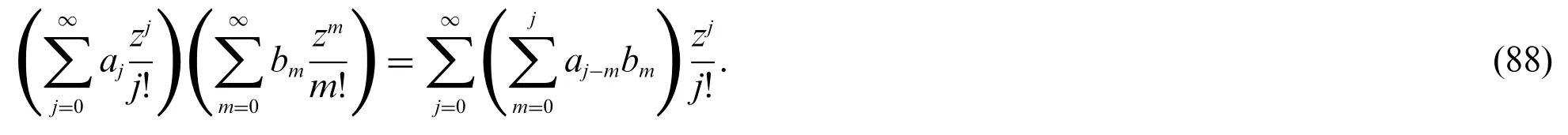
Now
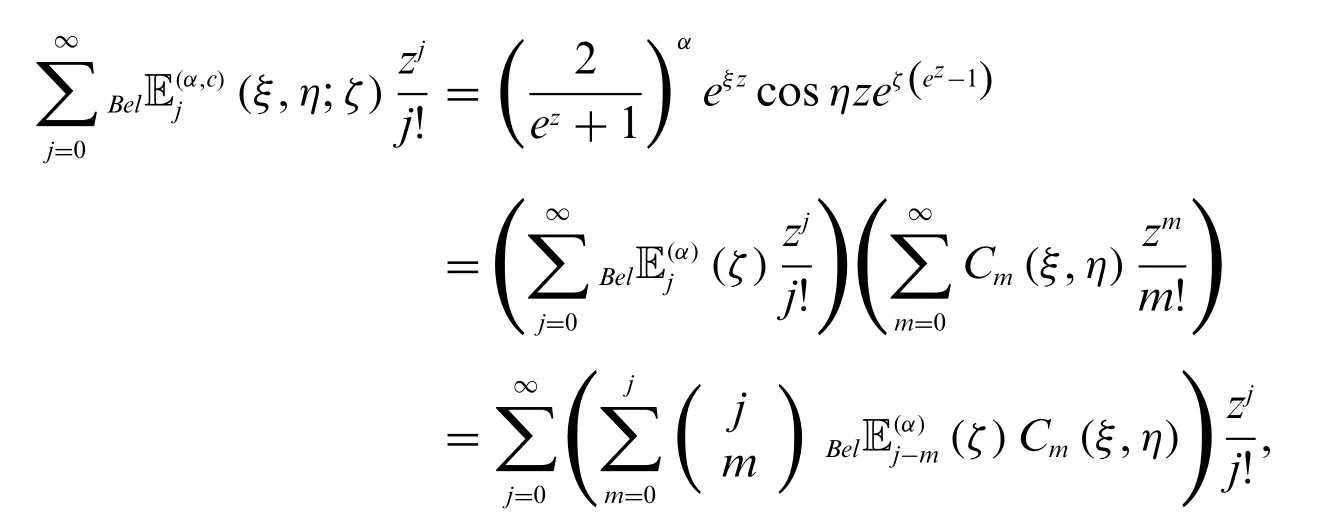
which proves(86).The proof of(87)is similar.
Theorem 3.4.Letj≥0.Then
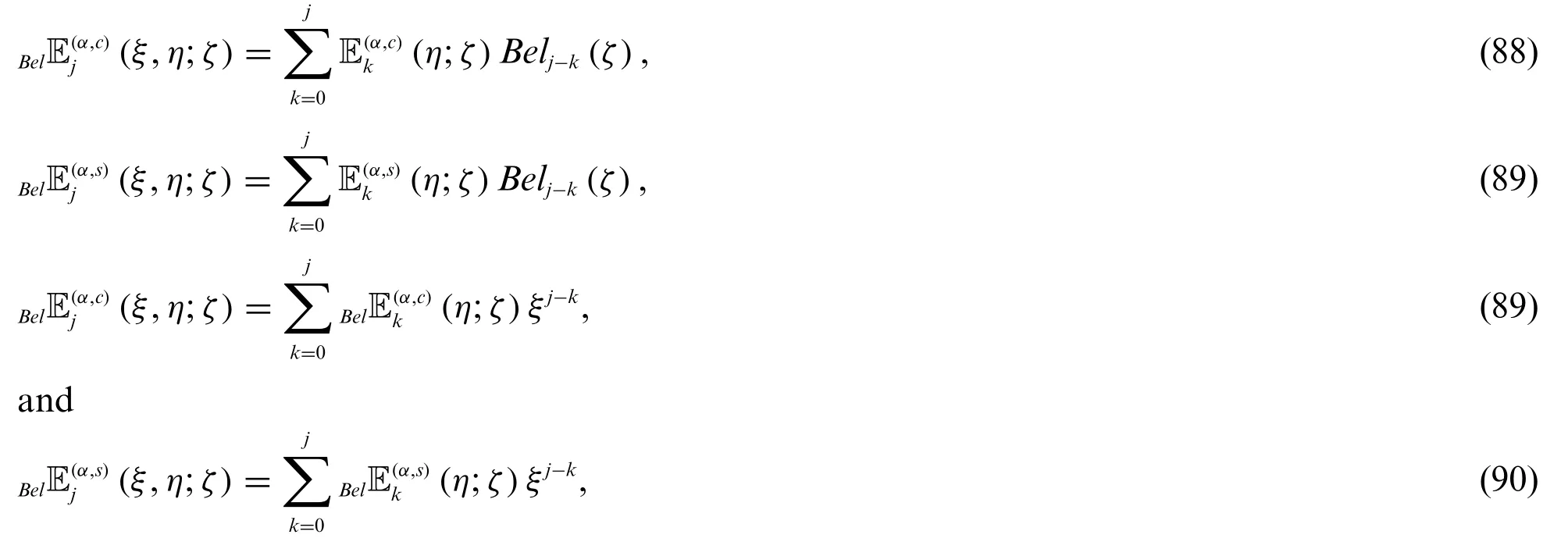
Proof.Using(72)and(73),we obtain(88)–(90).Here,we omit the proof of the theorem.
Theorem 3.5.Letj≥0.Then
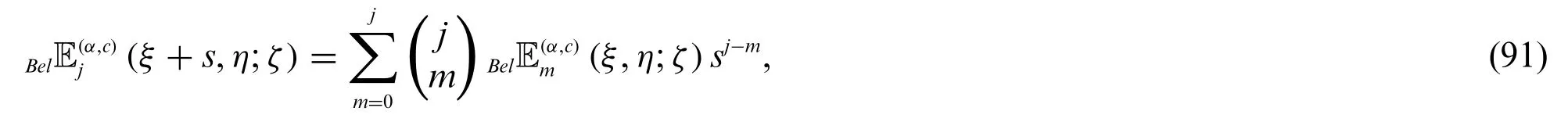
and
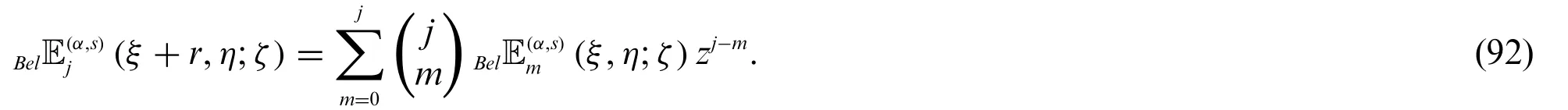
Proof.By changingξwithξ+sin(72),we have

which proves(91).The result(92)can be similarly proved.
Theorem 3.6.Letj≥1.Then

and

Proof.Eq.(72)yields

proving(93).Other(94)–(96)can be similarly derived.
Theorem 3.7.Letj≥0.Then
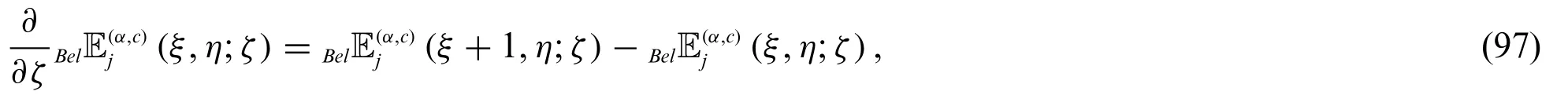
and

Proof.By definition(72),we have
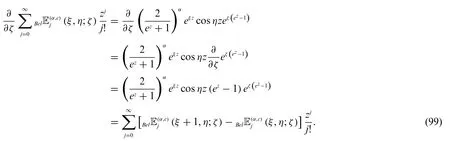
The complete proof of the result(97).The proof of(98)is similar.
Theorem 3.8.Letj≥0.Then

Proof.Using definition 3.1,we have
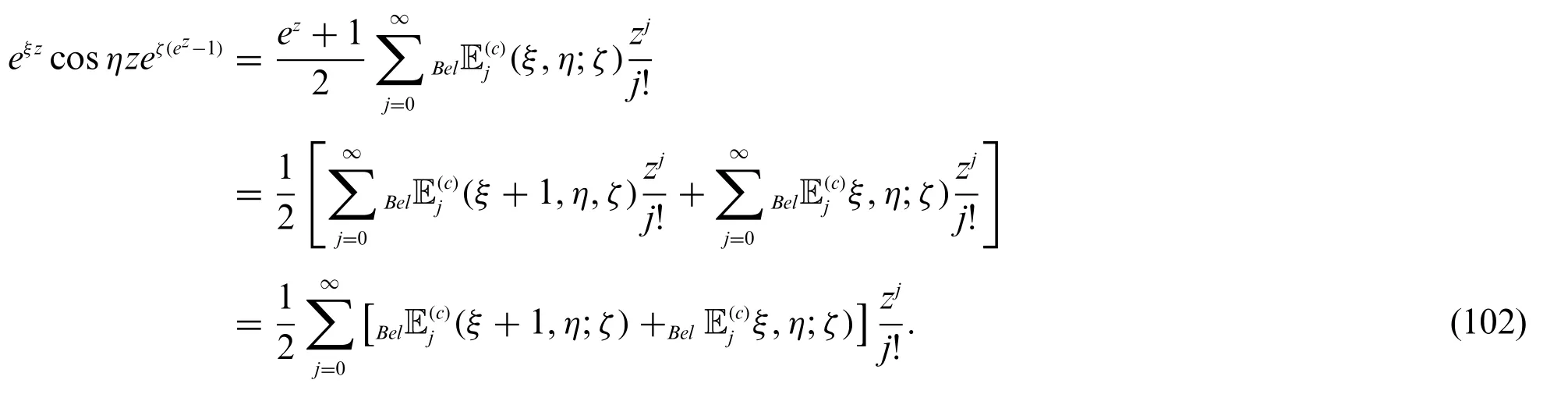
On the other hand,we have

In view of(102)and(103),we get(100).Similarly,we can easily obtain(101).
Theorem 3.9.Letj≥0.Then

and
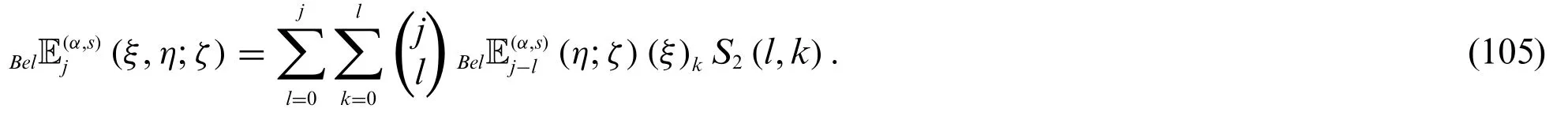
Proof.Using(7)and(72),we find
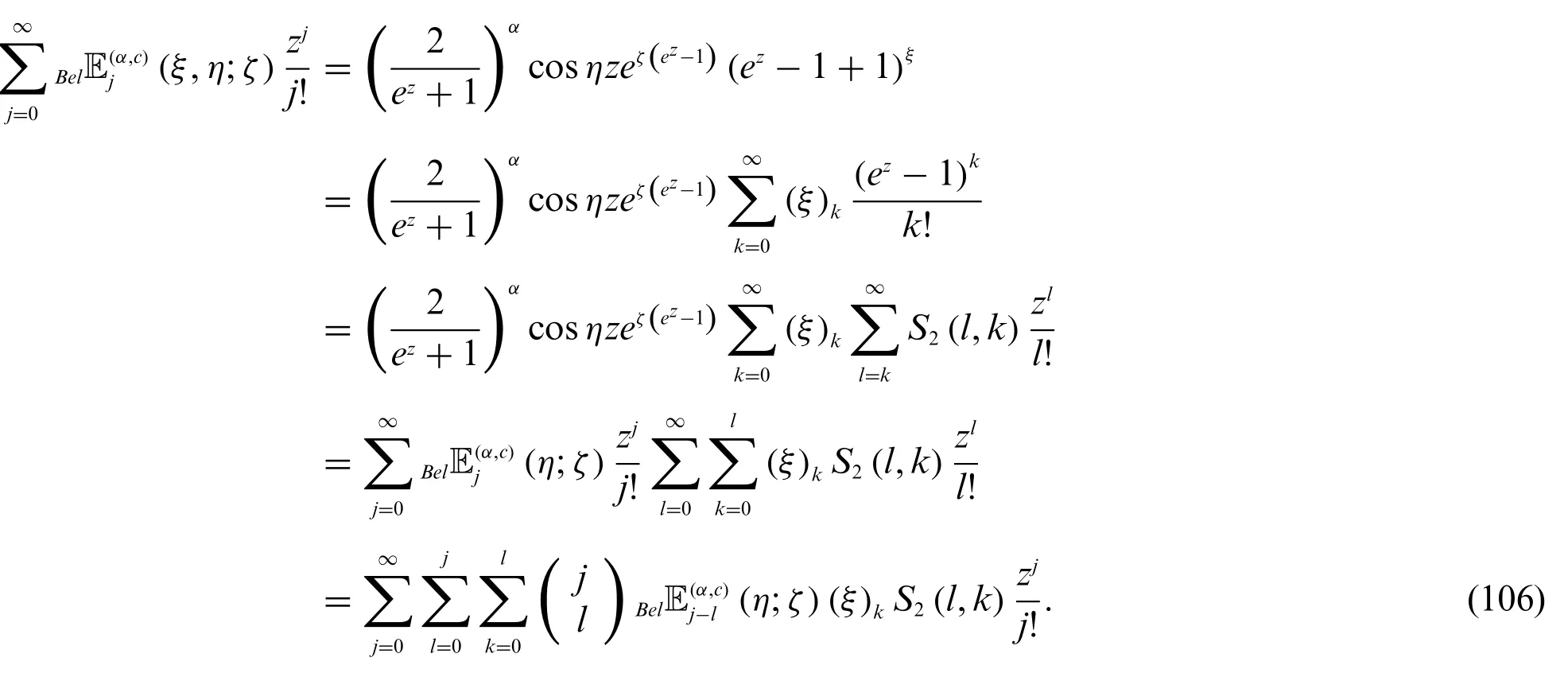
In view of(72)and(106),we get(104).Similarly,we can easily obtain(105).
4 Computational Values and Graphical Representations of Bell-Based Bernoulli Polynomials of Complex Variable
In this section, certain zeros of the Bell-based Bernoulli polynomials of complex variable,η;ζ)and,η;ζ)and beautifully graphical representations are shown.
The first few of them are
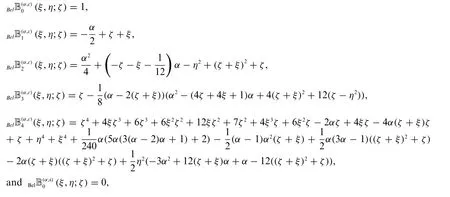

Table 1 shows some numerical values of Bell-based Bernoulli polynomials of a complex variable.
Table 1:Numerical values of Bell-based Bernoulli polynomials of a complex variable Bel(ξ,η;ζ)and Bel(ξ,η;ζ)

Table 1:Numerical values of Bell-based Bernoulli polynomials of a complex variable Bel(ξ,η;ζ)and Bel(ξ,η;ζ)
j BelB(α,c)j (5,6;2) BelB(α,s)j (5,6;2)0 1.0 0 1 6.0 6.0 2 1.83333 72.0 3-397.0 465.0 4-5123.9 840.0 5-38622.3 -21381.0 6-158258 -341508 7 505053 318760×101 8 1.81135×107 -2.1281×107 9 2.29789×108 -8.71221×108 10 2.19881×109 2.12412×108
Fig.1 shows the plot for the Bell-based Bernoulli polynomialBel(ξ,η;ζ)with(ξ,η;ζ)=(5,6;2).Fig.2 shows the plot for 3D Bell-based Bernoulli polynomialsBel(ξ,η;ζ).
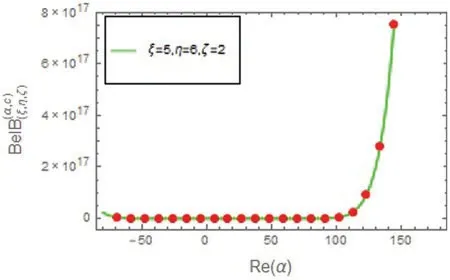
Figure 1:Bell-based Bernoulli polynomials Bel(ξ,η;ζ)
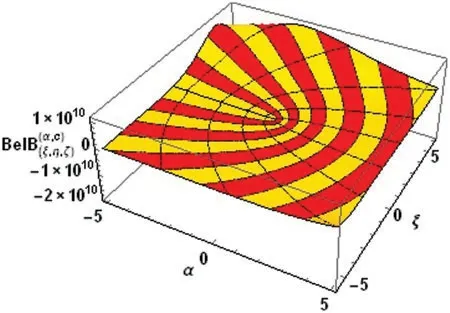
Figure 2:3D Bell-based Bernoulli polynomials Bel(ξ,η;ζ)
5 Computational Values and Graphical Representations of Bell-Based Euler Polynomials of Complex Variable
In this section, certain zeros of the Bell-based Bernoulli polynomials of complex variableBel(ξ,η;ζ)andBel(ξ,η;ζ)and beautifully graphical representations are shown.
The first few of them are

Table 2 shows some numerical values of Numerical values of Bell-based Euler polynomials of complex variable.
Table 2:Numerical values of Bell-based Euler polynomials of a complex variable (ξ,η;ζ)and(ξ,η;ζ)

Table 2:Numerical values of Bell-based Euler polynomials of a complex variable (ξ,η;ζ)and(ξ,η;ζ)
j BelE(α,c)j (5,6;2) BelE(α,s)j (5,6;2)0 1.0 0 1 6.0 6.0 2 1.5 72.0 3-403.0 459.0 4-5127.0 696.0 5-37282.0 -22914.0 6-132625 -345096 7 767443 -302880×101 8 1.93872×107 -1.80647×107 9 2.21045×108 -5.04831×107 10 1.91065×109 4.90648×108
Fig.3 shows the plot for the Bell-based Euler polynomial,η;ζ)with(ξ,η;ζ)=(5,6;2).

Figure 3:Bell-based Euler polynomials (ξ,η;ζ)
6 Conclusions
In the present article,we have considered the parametric kinds of Bell-based Bernoulli and Euler polynomials by making use of the exponential as well as trigonometric functions.We have also derived some analytical properties of our newly introduced parametric polynomials by using the series manipulation technique.Furthermore,it is noticed that,if we consider any Appell polynomials of a complex variable(as discussed in the present article),then we can easily define its parametric kinds by separating the complex variable into real and imaginary parts.Consequently,the results of this article may potentially be used in mathematics,mathematical physics and engineering.
Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement:This research was funded by Research Deanship at the University of Ha’il,Saudi Arabia,through Project No.RG-21 144.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
 Computer Modeling In Engineering&Sciences2023年4期
Computer Modeling In Engineering&Sciences2023年4期
- Computer Modeling In Engineering&Sciences的其它文章
- A Study of BERT-Based Classification Performance of Text-Based Health Counseling Data
- Overview of Earth-Moon Transfer Trajectory Modeling and Design
- CEMA-LSTM:Enhancing Contextual Feature Correlation for Radar Extrapolation Using Fine-Grained Echo Datasets
- The Class of Atomic Exponential Basis Functions EFupn(x,ω)-Development and Application
- Corpus of Carbonate Platforms with Lexical Annotations for Named Entity Recognition
- Unique Solution of Integral Equations via Intuitionistic Extended Fuzzy b-Metric-Like Spaces
