New Class of Doubt Bipolar Fuzzy Sub Measure Algebra

Shadia Majeed Noori,Abd Ghafur Ahmad and Shuker Mahmood Khalil

1Department of Mathematical Sciences,Faculty of Science and Technology,Universiti Kebangsaan Malaysia,Bangi Selangor,43600,Malaysia

2Department of Mathematics,College of Education for Pure Science,University of Tikrit,Tikrit,34001,Iraq

3Department of Mathematics,College of Science,University Basrah,Basrah,61004,Iraq

ABSTRACT The ideas of ambiguous bipolar skepticism under algebra and closed skepticism ambiguous bipolar ideals and related features have been developed.The fuzzy measure ideal is described in terms of bipolar ambiguous measure algebra and bipolar skepticism,and the linkages between bipolar fuzzy measure algebra are determined.A bipolar misty ideal’s skepticism is examined.In BCW and BCL-measure algebra,homogeneous ideas and dubious pictures of fuzzy bipolar measure ideas are examined.Also,we gave the relationship between these concepts.Finally,it is given the perfect terms for an occult bipolar doubt to be a measure of ideal fuzzy bipolar closed doubt.

KEYWORDS Fuzzy measure algebra;fuzzy measure;BCW-idials;BCF-ideals

1 Introduction

The BCK-algebras class has been identified as an appropriate subclass of the BCI-algebra class.Iséki et al.[1–4] proposed BCK/BCI-algebras as two key classes of Boolean algebra.BCK/BCIalgebra theory has spawned a plethora of literature since then.This gave a useful mathematical tool for modeling systems that were overly complicated or inadequately specified.Bipolar sets have been used in a variety of fields of mathematics since then.What is now known as fuzzy mathematics is the research of fuzzy sets and various implications in mathematics.Zhang et al.[5] was the first to propose bipolar fuzzy groups as a generalization of regular fuzzy groups[0, 1] in 1994.In addition,Lee[6]proposed a bipolar fuzzy group extension for fuzzy groups.Fuzzy dipole groups confer both a positive and negative membership score, while fuzzy groups confer a degree of membership in an element in a particular group.The interval[0,1]corresponds to positive membership degrees,while the interval[－1,0]corresponds to negative membership degrees.The range of degrees of membership in bipolar fuzzy groups is raised from period[0,1]to period[－1,1].Many operations and relations have been proposed to dipole fuzzy sets as a basis for investigating the enigmatic pole set theory[－1,1].Fuzzy dipole group theory has recently gained traction in a variety of fields,including group theory,half group theory,semifinal theorems,statistics,medicine,and among others.Rosenfeld[7]introduced a fuzzy subgroup of fuzzy algebraic structures.

There have been many contributions to the concepts of fuzzy subgroups and fuzzy ideal of doubt BCK/BCI-algebras by several researchers such as:Biswas[8]later proposed the concept of non-fuzzy subgroups of groups.The related characteristics of BCK-algebras using the fuzzy group notion are examined [9].Jun et al.have also researched fuzzy features of numerous ideas in BCK/BCI/RHOalgebras [10–21].Huang [22], on the other hand, are concerned with BCI algebra in other ways.To avoid confusion resulting from,Huang’s definition of perturbation BCI-algebra[23],Jun[24]proposed the definition of the fuzzy sub-algebra of doubt and the fuzzy ideal of doubt BCK/BCI-algebras and offered some conclusions concerning them.Following that, Zhan et al.[25] added the concept of ambiguous skepticism to BCI-algebra ideals,as well as the concept of doubt opaque H ideals in BCK algebra.As a result of what was accomplished by the previous works, new concepts were proposed and circulated to fuzzy measure algebra.The objective of this work is to introduce the concept of BCW and BCM measure algebras in a bipolar fuzzy measure array with discussed properties in this study.Also,we introduce fuzzy bipolar measure algebra and bipolar fuzzy measure proverb,as well as examine associated aspects.Then,by doubting the set of positive segments at the t-level and doubting the set of negative s-level segments,we describe the doubtful fuzzy dipole measure sub-algebra and the questionable fuzzy dipole measure ideal.Also examined are the connections between the ambiguous dipole measure sub-algebra and the ambiguous dipole perfect measure sub-algebra.Finally,we study homogenous and doubt images of putative fuzzy bipolar measure ideals in BCW and BCM-measure algebras.Moreover, we define the conditions under which a perfect fuzzy dipole measure model becomes a fuzzy closed dipole model.

2 Preliminaries

Definition 2.1.[26]A functionalμ:T→R+is called aσ-additive measure if whenever a setA∈Tis a disjoint union of an at most countable sequence(whereMis either finite orM=∞)thenu(A)=IfM= ∞then the above sum is understood as a string.If this property applies only to the finite values ofM,then μ is a final additive measure.

Definition 2.2.[27]LetWbe a universe of discourse,then a fuzzy set(FS)T is characterized by a membership functionμT(w)that takes values in[0,1].

Definition 2.3.[28].Let ∅J⊆F,whereFis BCK/BCI algebra.ThenJis a sub algebra ofFif∀ζ,η∈Jthenζ*η∈J.

Definition 2.4.[28].Let ∅J⊆F, whereFis BCK/BCI algebra.ThenJis an ideal ofFif it achieves the following:

1) 0 ∈J

2) ∀ζ,η∈F,ζ*η∈J,η∈J⇒ζ∈J.

Definition 2.5.[29].LetF∅.AnM-polar fuzzy measure set is a mapψ:F→[0,1]M.The membership value of anyζinFis defined by:

ψ(ζ)=(,,...,)where: [0,1]M→[0,1]is defined as thek-th function of projection.

Definition 2.6.[30] A fuzzy ordered set(X,μR)is called a fuzzy well-ordered set if it is a totally fuzzy ordered set in which every non-empty subset has a fuzzy least element.

Definition 2.7.[30](Zorn’s lemma)Let P be a partially ordered set.If every chain in P has an upper bound,then X has a maximal element.

Proposition 2.8.[30]If Zorn’s lemma holds,then fuzzy Zorn’s lemma holds.

3 BCW and BCM in Polar Fuzzy Measure Sub-Algebras

In this part,we give three concepts ofBCWandBCMin fuzzy measure algebra and with a study of its most prominent characteristics.

Definition 3.1.Let ∅J⊆FwhereFis fuzzy measure algebra.ThenJis aBCW－sub algebra ofFif(ζ*η)－1 ∈J,∀ζ,η∈J.

Example 3-1:A 3-polar fuzzy measure setψ:F={0,1,j,2}→[0,1]3by:

Soψis a 3-polar fuzzy measure ideal of F.

For each 3-polar fuzzy measure setψon F with= {σ1,σ2,σ3} ∈ [0,1]3, the setψ[ˇσ]=x ∈F:ψ(x)≥is BCM-sub algebra set of F because(J*η)2∈ψ[ˇσ], ∀J,η∈ψ[ˇσ]for the *-operation we can see the following Cayley table:

* 0 1 2 J 0 0 0 2 1 J J 0 2 J 1 1 1 0 2 2 2 2 1 0

Let K={0,1},then K is BCM-sub algebra of F.

Definition 3.2.Let ∅J⊆F,whereFis fuzzy measure algebra.ThenJis aBCM－sub algebra ofFif(ζ*η)2∈J∀ζ,η∈J.

Definition 3.3.Let ∅J⊆F,whereFisBCWandBCMfuzzy measure algebra.ThenJis an ideal ofFif it achieves the following:

1) 0,1 ∈F.

2) ∀ζ,η∈F,(ζ*η)2∈J,η∈J⇒ζ2∈J.

Definition 3.4.A fuzzy measure effect algebra is a system(F,M,0F,u,⊕)consisting of a setF,Mis fuzzy measure on bolean algebra,special elements 0Fanduare called the zero and the unit respectively,and a totally defined binary operation ⊕onF,called the ortho sum if for allh,ℓ,λ∈F:

1) Ifh⊕ℓand(h⊕ℓ)2⊕λare defined,thenℓ⊕λandh⊕(ℓ⊕λ)are defined andh⊕(ℓ⊕λ)2=(h⊕ℓ)2⊕λ.

2) Ifh⊕ℓ2is defined,then(ℓ⊕λ)2=(ℓ⊕h)2,alsoℓ2⊕his fuzzy measure set.

3) ∀h∈F,there is a uniqueℓ∈Fsuch thath⊕ℓ2is fuzzy measure set andh⊕ℓ2=u.

4) Ifh⊕uis fuzzy measure set defined,thenh=0F.

Example 3.11.LetF={0,ι2,3,6}beBCWandBCM-fuzzy measure algebra with Cayley table defined by a mappingF→[0,1]3:

4 M-Polar(α,β)-Fuzzy Measure Ideals

In this part,we suggest and discussion this conceptM-polar(α,β)-BCMandBCI2fuzzy measure ideals,where:α,β∈{∈,δ,∈∨δ,∈∧δ},α∈∧q.

Proposition 4-1.Let℘be anM-polar fuzzy measureM-PFM ofF,the set℘1∅,∈(0.25,1]mis an ideal ofFif and only if℘such that the assertions below:for allx,y∈F,

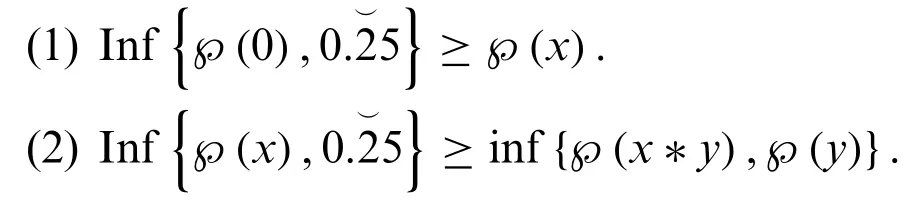
Theorem 4.5.Let℘be anM-PFMI subset ofFandξbe an ideal ofFsuch that,

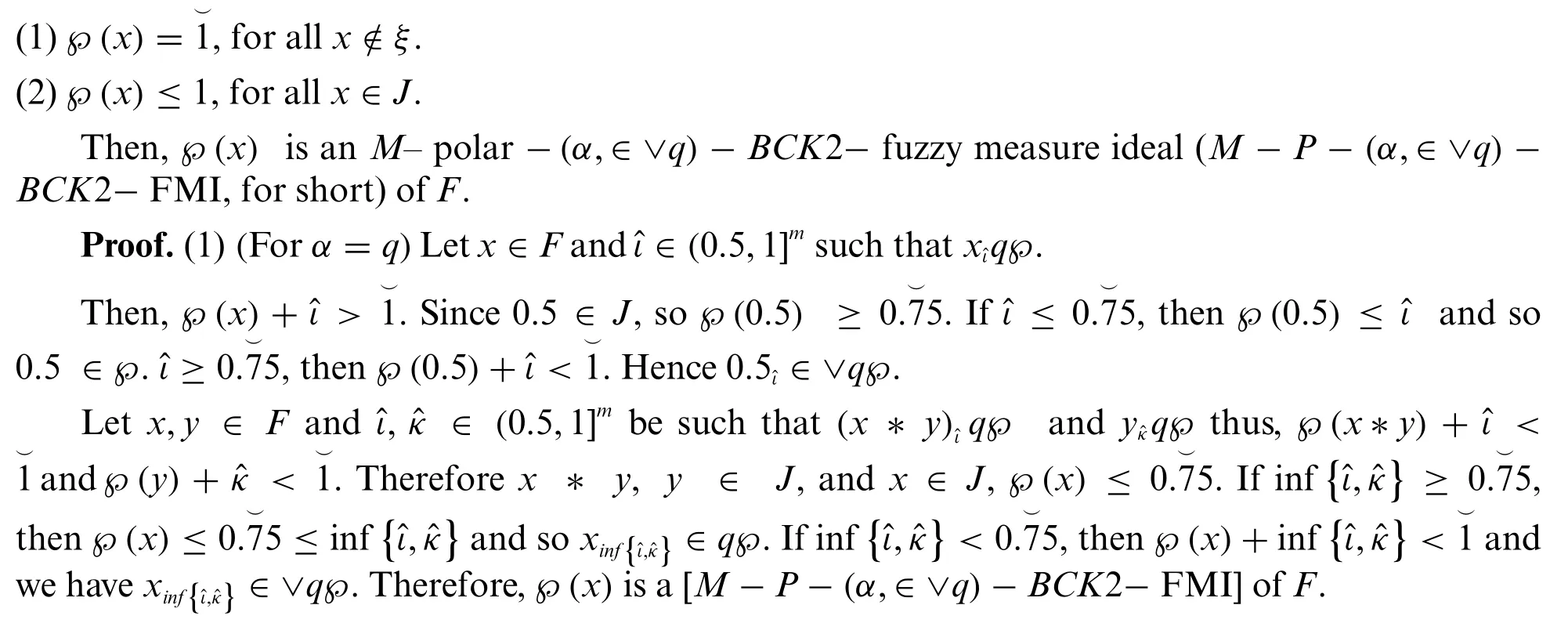
Theorem 4.6.Suppose that℘is an-ideal subset ofFandξbe an ideal ofFsuch that

Then,℘(x)is an(M－P－(α,∈∨q)－BCK2－FMI,for short)ofF.

Proof.Similarly,to the proof of Theorem 4.5.

Theorem 4.7Let℘be an-ideal subset ofFandξbe an ideal ofFsuch that

Then,℘(x)is an[M－P－(α,∈∨q)－BCK2－FMI]ofF.

Proof.Similarly,to the proof of Theorem 4.5.

5 Conclusions

We got a new class ofBCWandBCMmeasure algebra based on polar fuzzy measure sets.We looked at characterizations of the blurry polar measure sub-algebra and fuzzy (commutative)measure ideals of polarity.We also have discussed the relationships among polar fuzzy measure sub algebras,andM-polar ambiguous and ambiguous pole reciprocal ideals.Concepts suggested in this article can be extended to different types from the ideals inBCWandBCM-measure algebras, for instance,a-ideal,implicated,n-fold andn-fold ideals commutative measure ideals.We also deduced a new concept calledM-polar(α,β)-BCWandBCM-fuzzy measure algebras and some specific results for it.We investigatedM-polar(α,β)-BCWandBCM-fuzzy measure algebras measure ideas with relationships related to them.Finally,we defined the criteria under which a closed doubt bipolar fuzzy idea can exist.We feel our findings in this paper will serve as a foundation for further research into the algebraic structure ofBCWandBCM-algebras.In future work,the concepts ofM-polar(α,β)-BCWandBCMcan be generalized in other topics such as graph topology,graph algebra and other topics.

Authors’Contributions:All authors read and approved the final manuscript.

Funding Satement:We received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.