A Dimension-Splitting Variational Multiscale Element-Free Galerkin Method for Three-Dimensional Singularly Perturbed Convection-Diffusion Problems

Jufeng Wang,Yong Wu,Ying Xu and Fengxin Sun

1College of Finance&Information,Ningbo University of Finance&Economics,Ningbo,315175,China

2Faculty of Science,Ningbo University of Technology,Ningbo,315016,China

ABSTRACT By introducing the dimensional splitting (DS) method into the multiscale interpolating element-free Galerkin(VMIEFG)method,a dimension-splitting multiscale interpolating element-free Galerkin(DS-VMIEFG)method is proposed for three-dimensional (3D) singular perturbed convection-diffusion (SPCD) problems.In the DSVMIEFG method,the 3D problem is decomposed into a series of 2D problems by the DS method,and the discrete equations on the 2D splitting surface are obtained by the VMIEFG method.The improved interpolation-type moving least squares (IIMLS) method is used to construct shape functions in the weak form and to combine 2D discrete equations into a global system of discrete equations for the three-dimensional SPCD problems.The solved numerical example verifies the effectiveness of the method in this paper for the 3D SPCD problems.The numerical solution will gradually converge to the analytical solution with the increase in the number of nodes.For extremely small singular diffusion coefficients,the numerical solution will avoid numerical oscillation and has high computational stability.

KEYWORDS Dimension-splitting multiscale interpolating element-free Galerkin (DS-VMIEFG) method; interpolating variational multiscale element-free Galerkin (VMIEFG) method; dimension splitting method; singularly perturbed convection-diffusion problems

1 Introduction

In view of the advantage that the construction of the approximation function is only related to the discrete point and not related to the grid, the meshless method has received a lot of attention from many scholars in recent years [1–4].Meshless methods have been widely used in scientific and engineering problems and have shown high accuracy and effectiveness[5–9].

Based on various construction methods of approximation functions or various discrete methods of the problem to be solved,many meshless methods have been proposed[10–14].The ordinary leastsquares (OLS) method is the best approximation [15], and it has been applied in engineering fields widely[16,17].Based on the OLS method,Lancaster et al.presented the moving least-squares method(MLS) approximation [18], which is one of the common methods used to construct approximation functions and has a wide range of applications in meshless [18].Many meshless methods have been proposed based on the MLS method,such as element-free Galerkin method[19],smoothed particle hydrodynamics [20] and meshless local Petrov-Galerkin method [21].From the research of many scholars, the meshless method based on MLS has better effectiveness [22].Based on MLS, some improved methods have also been proposed,such as complex variable moving least squares method[23,24],interpolation-type moving least-squares(IMLS)method[25].To avoid the singularity of the weight function, Cheng et al.[26–28] also proposed an improved interpolation-type moving least squares(IIMLS)method with non-singular weights.

The element-free Galerkin (EFG) method, which couples the Galerkin weak form and the MLS method,is a widely used mesh-free method[29].In order to directly apply essential boundary conditions,the interpolating element-free Galerkin(IEFG)method is proposed by coupling the IMLS method [28,30–33].The IEFG method not only has the advantage of directly applying boundary conditions but also has the advantage of having a smaller radius of influence compared to EFG under the same basic functions.The IEFG method has been applied to potential problems [34,35],elastoplasticity problems [28], crack problems [36], structural dynamic analysis [37], prevention of groundwater contamination [38], elastoplasticity problems [39], Poisson equation [40], elastic large deformation problems[41],Oldroyd equation[42],etc.

To improve the computational efficiency of the EFG method, by introducing the dimension splitting method[43],Cheng et al.proposed the dimension splitting element-free Galerkin(DS-EFG)method [44] and dimension splitting interpolating element-free Galerkin (DS-IEFG) method [45].The dimension splitting meshless method greatly improves the computational efficiency of the EFG method,and shows high computational efficiency and accuracy for 3D advection-diffusion problems[46],3D transient heat conduction problems[47–49],3D elasticity problems[50],3D wave equations[51,52],etc.

For some fluid problems with large Reynolds numbers, the solution of EFG method may have non-physical oscillations.In order to avoid the physical oscillation,Ouyang et al.[53]proposed the variational multiscale element-free Galerkin(VMEFG)method by introducing variational multiscale(VM)method.The VMEFG method has high stability for fluid problems with large Reynolds numbers or singular disturbances[2,54,55].Similar to the EFG method,the DS-EFG method is also prone to nonphysical oscillations for singularly perturbed fluid problems.By coupling the VM and DS-EFG methods, Wang et al.presented the hybrid variational multiscale element-free Galerkin method for 2D convection-diffusion[4,56]and 2D Stokes problems[57].

The convection-diffusion (CD) equation plays an important role in some physical problems[58,59], such as the transport of the quantity in air and river pollution.Since it is often difficult to obtain analytical solutions, many scholars have studied numerical methods to obtain approximate solutions.Numerical instability is prone to occur when the CD problem contains large Reynolds numbers or singularly perturbed diffusion coefficients[4].Stabilization techniques must be added to numerical methods to avoid numerical oscillations of the solution.Varying the shape parameter, a finite-difference method based on the radial basis function is introduced for 2D steady CD equations with large Reynolds’ numbers [60].Aga presented an improved finite difference method for 1D singularly perturbed CD problems [61].Using the collocation method of high-order polynomial approximation, Ömer studied the numerical solution of 3D CD problems with high Reynolds [62].Zhang et al.[63] presented a VMIEFG method for the singularly perturbed two-dimensional CD problems.

In this paper, by introducing the dimension splitting (DS) method into the VMIEFG method,we will develop a dimension splitting multiscale interpolating element-free Galerkin(DS-VMIEFG)method for three-dimensional singular perturbed convection-diffusion(SPCD)problems.In the DSVMIEFG method,the DS method is used to decompose the 3D problem into a series of 2D problems,and the discrete equations on the 2D splitting surface will be obtained by the VMIEFG method.The IIMLS method is used to construct shape functions in the weak form and to combine 2D discrete equations into a global system of discrete equations for the three-dimensional SPCD problems.And some numerical examples will be solved to verify the effectiveness of the DS-VMIEFG method.

2 The IIMLS Method

In order to overcome the insufficiency that the weight function must be singular in the IMLS method, by coupling the interpolation function transformation and MLS approximation, Cheng et al.[26] presented the IIMLS method.In this method, the approximation function satisfies the interpolation property,and the weight function is also non-singular.

Letpi(x)(i=1,2,···,m)andw(x－xI)be the basis functions and nonsingular weight functions used in the IIMLS method.The approximation of the IIMLS method is

where xI(I=1,2,···,n)is the node whose influencing domain covers x ∈Rn,andΦI(x)is the shape function given by

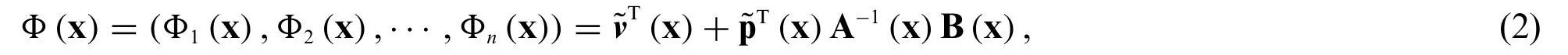
with

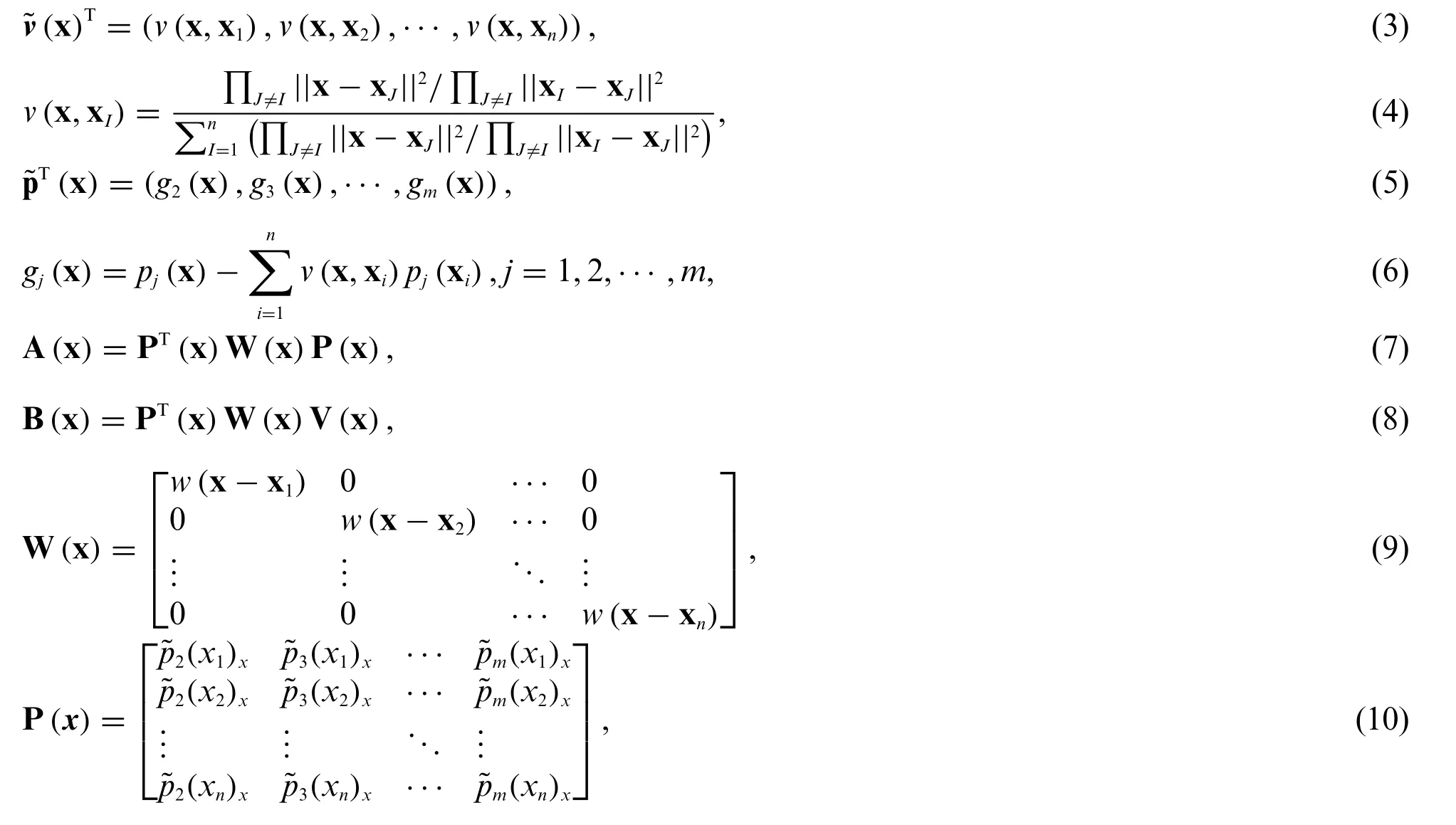
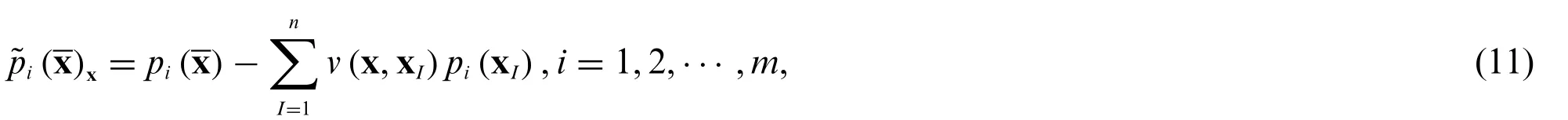
The element in thei-th row andj-th column of matrix

3 The DS-VMIEFG Method for 3D SPCD Problems

The following stationary three-dimensional convection-diffusion problem is considered:

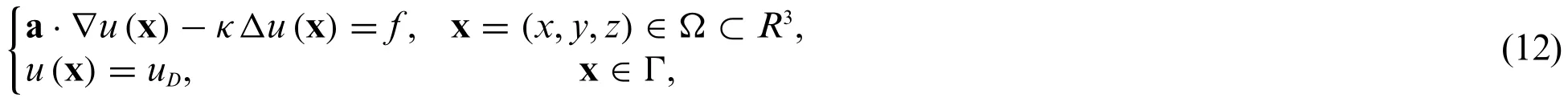
wherefis a known source term and Γ is the boundary of domain Ω.u=u(x)is an undetermined function,a=(a1,a2,a3)Tis the velocity field,κ≪0 is the very small diffusion coefficient,anduDis a prescribed function on the boundary.

By using the dimension splitting method,the problem in(12)can be transformed into a series of 2D problems on the coordinate plane of(x,y):

wherezk,(k=0,1,2,···,L)denote the discretized nodes in the dimension splitting direction onz,f|z=zkf (x,y,zk)and Ωk⊂R2(k=0,1,2,···,L)denote the dimension splitting plane such that

Define the subscript notation in partial derivatives as

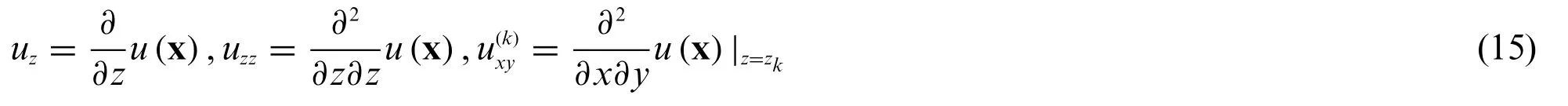
The variational weak form of Eq.(13)is

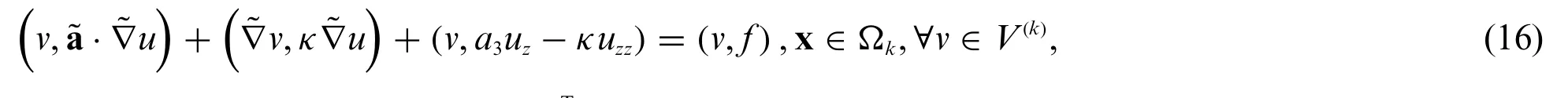
Using the variational multiscale method, the functions are broken down into two parts of the coarse and fine scales as

From Eqs.(18)and(16),we have

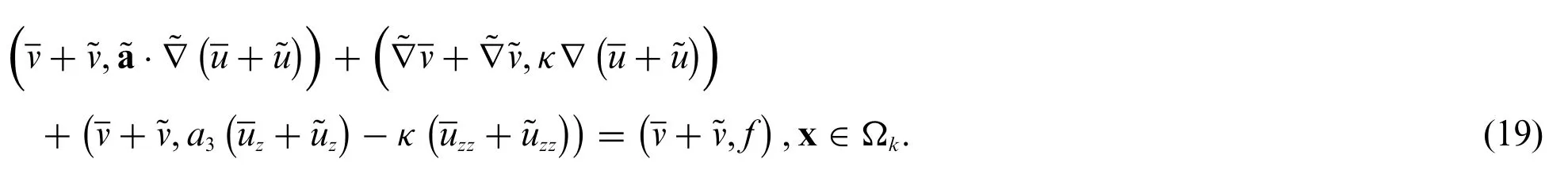
Decomposing Eq.(19)into coarse-scale and fine-scale parts leads to

and

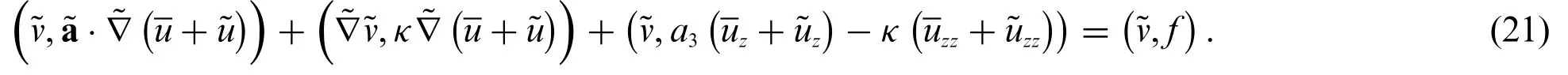
From Eq.(21),it follows that

On the boundary, the fine-scale function can be seen as zero.The coefficient ccellhas the following form

where λcell(z)is solved from the ordinary differential equation with zero boundary conditions:

Then it follows that

whereτ=

Omitting the superposed bars and coupling Eqs.(20)and(33),we have

where

The summation expression in Eq.(34) denotes the effect of the fine scale for obtaining stale solutions.

On Ωk,define the numerical solution space as

where Φi(x)is solved from the IIMLS method on the 2D splitting surface Ωk.

Omitting the higher derivatives in the stability term, from Eq.(37), we can obtain the linear equations as

where u(k)is the vector formed by the value to be evaluated on the node in Ωk,and

Eq.(38)is the discrete system of equations on the 2D dimension-splitting surface Ωk.Next,the global discrete equations on Ω will be realized in thezdirection using the IIMLS method.It follows from the IIMLS method that

where Φi(zk)is calculated by the IIMLS method in thezdirections,and Λ(xk)is the index set of nodes in influence domain of nodezk.

Using Eqs.(46)and(47)and the interpolating property,the whole discrete equations of the DSVMIEFG method for the 3D SPCD problems can be assembled as

Substituting the boundary condition into Eq.(48)directly,the solutions for the three-dimensional convection-diffusion problem will be solved from Eq.(48).

4 Numerical Examples

In this section,the validity of the method of this paper will be verified by two examples.We take the cubic spline function as the weight function in the IIMLS method.The integration scheme uses a rectangular 4×4 Gaussian numerical integration.Leth1,h2andh3represent the node spacing in thex,yandzdirections,respectively.On the two-dimensional split surface,the influence domain of the node is rectangular with radius dmax×(h1,h2),and dmax is a scalar to adjust the precision of the solution.In Eq.(48),the radius of influence domain is dmax2×h3.And the linear and quadratic basis functions are used in Eqs.(36)and(46),respectively.

Define the relative error by

whereuhis the numerical solution andNis number of all discrete nodes.

Example 1.The first consideration is a singularly perturbed convection-diffusion problem on a cube with an exact solution as

The velocity field parameters are fixed to be= 1.When the small diffusion coefficient isκ=10－9and the regular 41×41×21 nodes distribution is used,the contour distribution of the exact solution and the numerical solution of the method of this paper atz=0.1,0.3,0.5,0.7,0.9 are shown in Figs.1a and 1b with dmax=1.2.And the corresponding numerical solution of the DSEFG method without the stable term is shown in Fig.1c.From Fig.1,we can see that the DS-EFG method without coupling the VM method cannot obtain the stable solution for the CD problems with an almost singular diffusion coefficient.However,the method in this paper can still bring stable numerical solutions in the case of extremely small diffusion coefficients.

Figure 1:The contour distribution of the exact and numerical solutions at z=0.1,0.3,0.5,0.7,0.9 for Example 1

When the small coefficients are respectivelyκ= 10－6,10－9,10－12,10－15,10－18, the corresponding relative errors for 41×41×21 and 65×65×26 regular nodes distributions are shown in Table 1.The results show that for almost singular diffusion coefficients,our method of this paper still has a very stable solution.

When the nodes distribution is 41×41×21, the relative errors for different values of dmax =1.1,1.2,···,3 are given in Fig.2.This figure shows that the DS-VMIEFG method of this paper has higher numerical accuracy when dmax is around 1.2.

Table 1: The relative errors for different diffusion coefficients

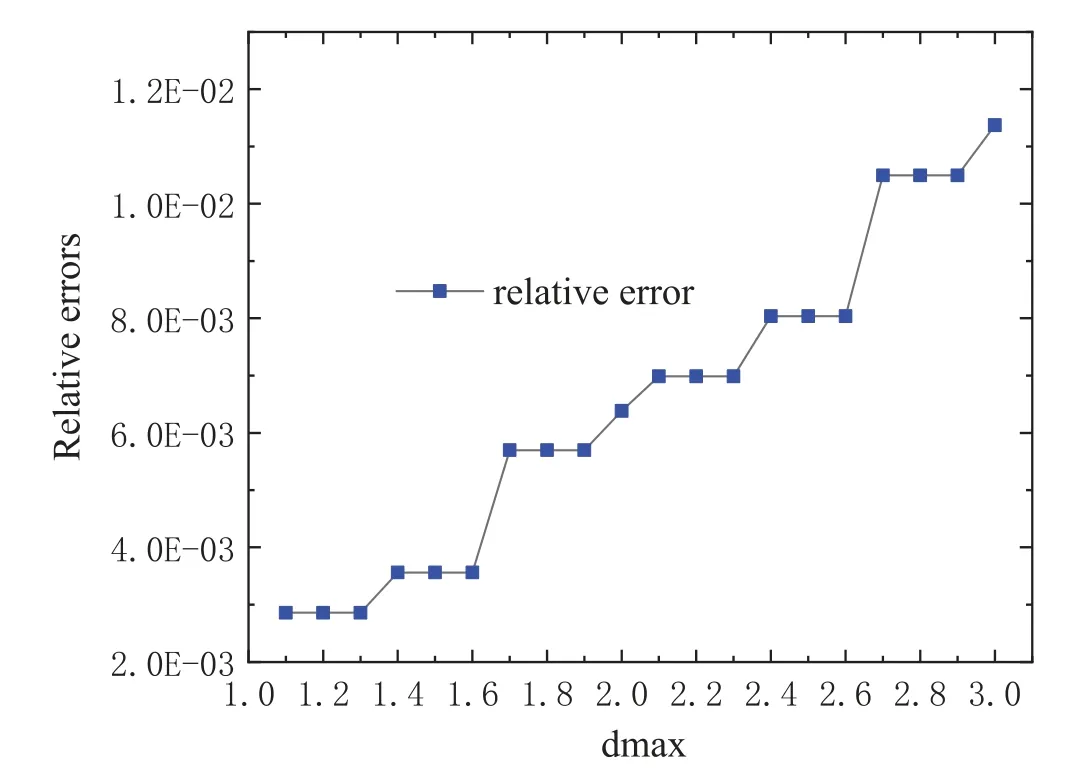
Figure 2:The relative errors for different values of dmax=1.1,1.2,···,3 with the nodes distribution 41×41×21

To study the convergence, when there are 21 splitting points in thezdirection and 17 × 17,33×33,65×65,129×129 nodes on the 2D splitting surface,the relative errors are shown in Fig.3.It can be seen that as the number of nodes increases,the numerical solution gradually converges to the exact solution.

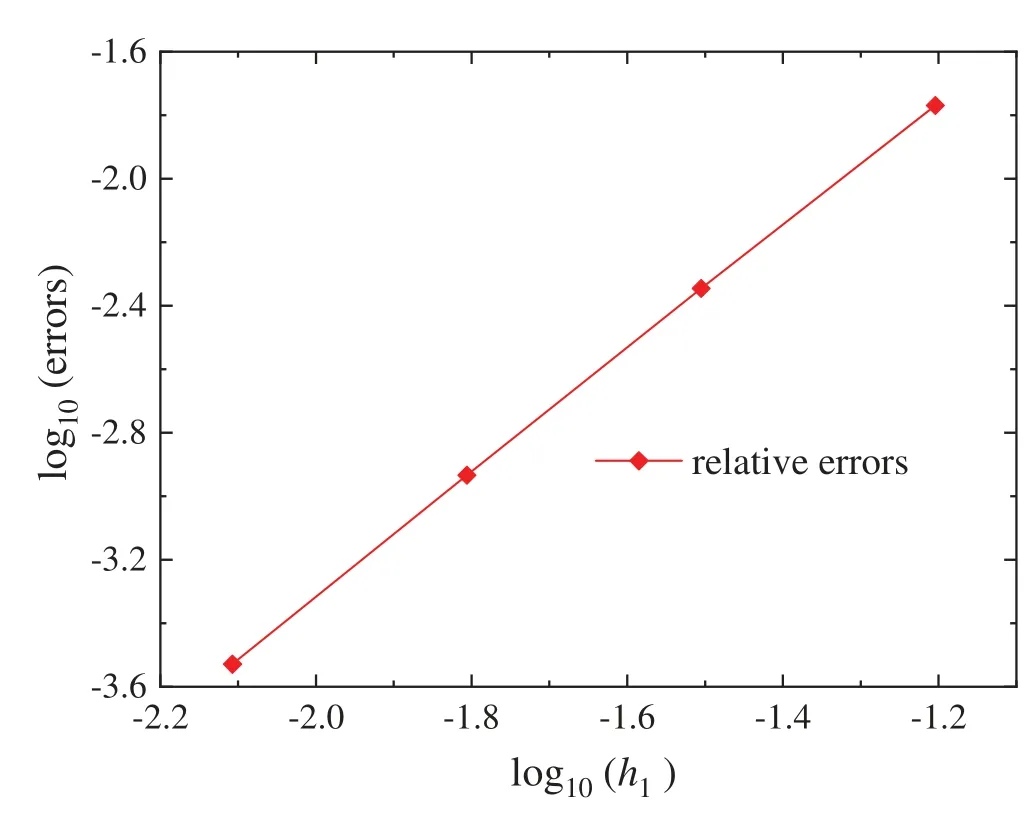
Figure 3: The relative errors for different regular nodes distribution of 17 × 17, 33 × 33, 65 × 65,129×129 nodes on the 2D splitting surface with dmax=1.2 and h3 =0.05

Example 2.The second considered convection-diffusion problem has the following exact solution as[62]

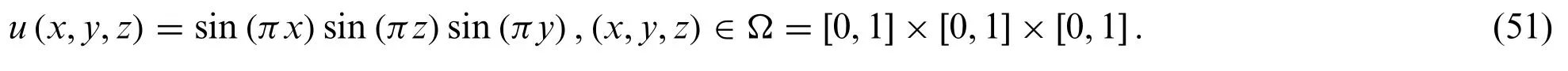
The parameters area1= cosα·cosβ,a2= cosα·sinβ,a3= sinα,whereα= 35o,β= 45o.The source termfand the boundary conditions are obtained from the analytical solution of Eq.(51).

Whenκ=10－9and applying the regular 41×41×21 nodes distribution,we presented the contour distribution of the solution atz= 0.1,0.3,0.5,0.7,0.9 in Fig.4 with dmax = 1.2.And results of the method of this paper and the DS-EFG method are respectively shown in Figs.4b and 4c.The numerical results of our method agree well with the exact.However,the contours solved by the DSEFG method have obvious oscillations.

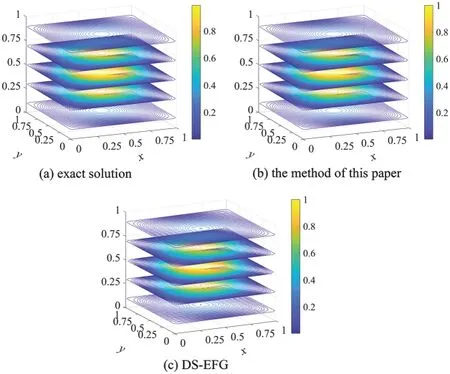
Figure 4: The contour distributions of the exact and numerical solutions at z = 0.1,0.3,0.5,0.7,0.9 for Example 2

Whenκ= 10－6,10－9,10－12,10－15,10－18, the corresponding relative errors for 41 × 41 × 11 and 65×65×21 regular nodes distributions are shown in Table 2.It can be seen from the results that the DS-VMIEFG method in this paper can still obtain higher precision solutions for the convectiondiffusion problems with high singular diffusion coefficients.

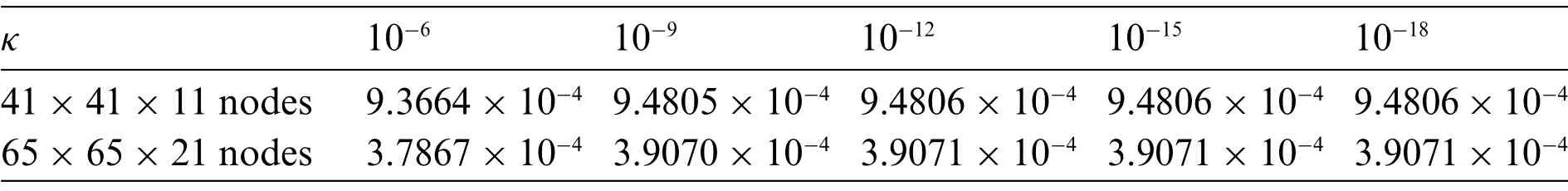
Table 2: The relative errors for different diffusion coefficients of Example 2

When using the regular 41×41×11 nodes distribution, we plot the relative errors of different dmax= 1.1,1.2,···,3 in Fig.5.It can be seen that when the value of dmax is around 1.2,the method in this paper can obtain higher calculation accuracy.

When 21 splitting points are fixed in the z direction,for different node distributions of 17×17,33×33,65×65,129×129 nodes on the 2D split plane,the relative errors are shown in Fig.6.The results show that the solution of the numerical method in this paper is convergent.

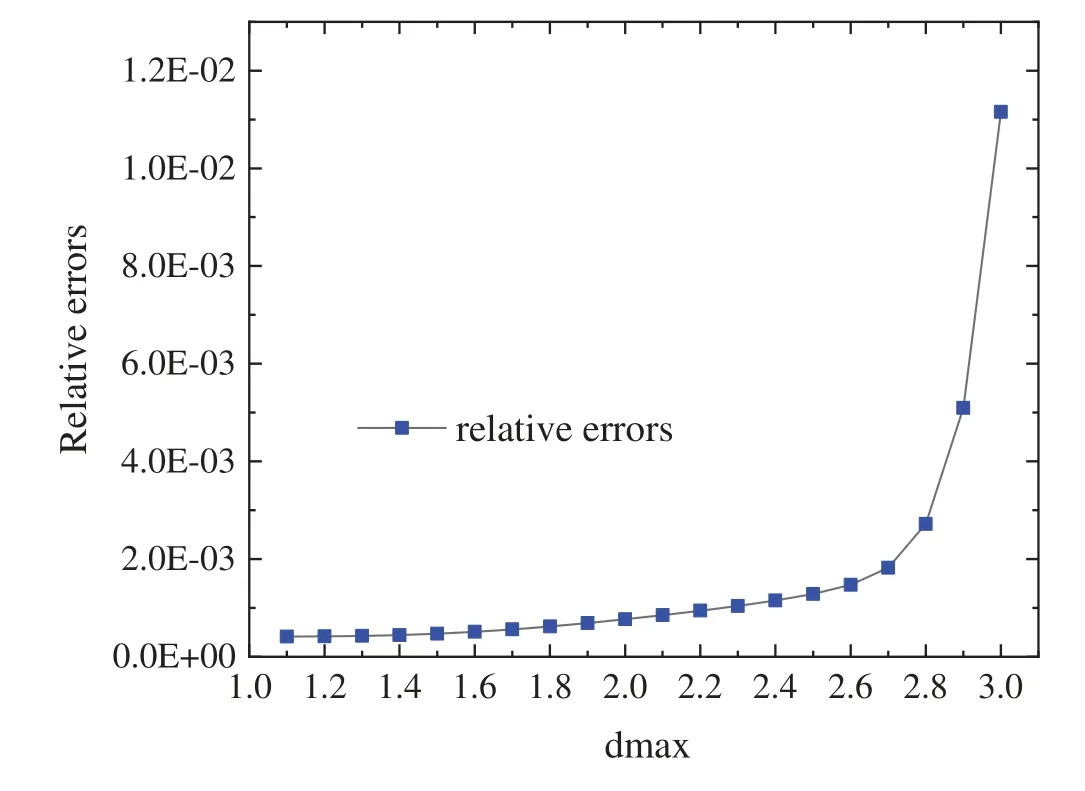
Figure 5:The relative errors for different values of dmax=1.1,1.2,···,3 with the nodes distribution 65×65×11 for Example 2

Figure 6: The relative errors for different regular nodes distribution of 17 × 17, 33 × 33, 65 × 65,129×129 nodes on the 2D splitting surface with dmax=1.2 and h3 =0.05 for Example 2

5 Conclusions

By introducing the DS method into the VMIEFG method, a DS-VMIEFG method for threedimensional singular perturbed convection-diffusion problems is presented in this paper.In the DS-VMIEFG method, the 3D problem is decomposed into a series of 2D problems, and then the weak form of the Galerkin integral is only established on the 2D splitting surfaces by the VMIEFG method.The DS-VMIEFG method can avoid the construction of integral weak form on the 3D domain.The IIMLS method is used to obtain the shape functions in the weak form and to combine 2D discrete equations into a global system of discrete equations for the 3D SPCD problems.The numerical example verifies the effectiveness of the DS-VMIEFG method in the case of very small singularly perturbed diffusion coefficients, and the numerical solution can avoid non-physical numerical oscillations.

Funding Statement:This work is supported by the Natural Science Foundation of Zhejiang Province,China(Grant Nos.LY20A010021,LY19A010002,LY20G030025),and the Natural Science Foundation of Ningbo City,China(Grant Nos.2021J147,2021J235).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.