人造肉脂肪组织3D打印轨迹规划算法
陈廉杰 宁 萌 陈慧涛 张 帆
(1.江南大学机械工程学院,江苏 无锡 214122;2.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
3D打印技术目前已被广泛应用于生物、食品、机械和航空航天等工业领域,但其仍面临诸多问题与挑战[1]。近年来,伴随着人造肉发展的浪潮,人造肉3D打印技术被各国大力研究,理论上可通过3D打印制造出各种形态复杂与营养均衡的可满足大部分人群饮食所需的既科学又能产生食欲的肉制品[2]。在人造肉3D打印技术中最常见的打印方法有挤出式与喷墨式两种[3-4]。研究拟采用基于熔融堆积(FDM)的3D打印技术,将海藻酸钠包裹植物油脂并与琼脂结合所得原料作为人造肉脂肪部分打印原料,其原理如图1所示,在喷头内向物料施加压力使其以丝状形态挤出,并在喷口处逐渐降温,以所设置运动轨迹在平台上冷却堆积形成成品。

图1 打印原理图
相比于常见聚乳酸(PLA)与丙烯腈—丁二烯—苯乙烯共聚物(ABS)等材料3D打印技术,国内外关于人造肉3D打印轨迹规划的研究仍然较少。人造肉原料各项物理性质均与常规固体材料不同,其在喷头内处于熔融态,打印后在平台上由于热传导时间问题原料仍会保持极短暂的不稳定流动状态,若处理不好,最终会影响成品质量。目前对于人造肉3D打印运动轨迹路径大多仍采用常规材料的运动算法,如平行扫描法[5-7]、星形发散扫描法[8]或分形扫描法[9-10]等,在实际打印中将会导致打印物料在轨迹交互与拐角处坍塌堆积从而产生大象脚现象。
针对以上问题,研究提出一种人造肉脂肪组织3D打印成型轨迹优化算法,采用贝叶斯算法库进行模型切片层分区处理,结合遗传算法与蚁群算法并通过扫描最优运动路径角度,同时对传统的zigzag路径扫描法进行改进,减少运动路径中的尖角与拐角及打印喷头的间断次数,以此对运动路径进行优化,实现符合3D打印人造肉的打印运动轨迹的合理规划。
1 设计思路与方法概述
zigzag扫描法因其算法简单以及与硬件适配度高,在人造肉3D打印领域应用较为广泛。3D打印对象为基于植物原料的人造肉制品,要求成品纹理能够模拟真实动物肉制品复杂纹理[11]。若采用传统zigzag扫描法,作业时对于复杂纹理填充会使得运动路径过渡点与拐角增多且喷头频繁间断,导致打印效率与成品质量严重下降。研究基于贝叶斯算法并结合实际情况,对传统zigzag扫描算法进行适配于3D打印人造肉的优化处理,对运动轨迹进行合理有效规划,同时通过试验不断提高整体优化效果。其优化方法如图2所示。
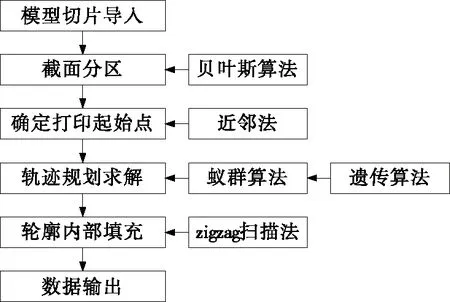
图2 轨迹规划流程图
具体实施步骤:
(1)对所需打印的人造肉进行建模与切片处理,并采用贝叶斯算法库对切片后的模型截面层进行分区处理以得到若干满足简单多边形特性的小型子分区。
(2)采用经改进的近邻法确定各子分区轮廓最优运动起始点。
(3)采用遗传算法和蚁群算法同时充分考虑成品质量与打印效率,对经分区处理得到的模型截面层子分区轮廓的打印轨迹进行合理规划。
(4)以zigzag扫描法为基础,进一步对截面子分区内部填充轨迹进行优化,减少尖角拐角的数量以此提高模型打印质量。
(5)输出优化处理结果,同时将计算所得优化轨迹输出为G代码用于3D打印并进行验证。
2 轨迹规划算法
2.1 截面分区处理
3D打印人造肉成品要做到仿真效果,首先在视觉上需要模拟真实动物肉制品纹理,因此喷头在对各细小花纹走线时每层截面都会产生数量与大小均不同的岛屿结构,此时传统的zigzag扫描算法会使喷头运动时产生过多的加减速与间断动作,降低打印效率与质量。因此在轨迹规划时首先需要对模型切片后含有岛屿的复杂截面层进行分区处理,分割成若干形状简单的小型连续子分区,为轮廓与内部纹理填充部分规划运动路径奠定基础,以实现各子分区的连续打印功能,最终减少打印喷头的运动中断次数,同时避免较长的打印运动路径带来的过大的剪切应力,从而可进一步提高打印成品质量[12]。
采用经keil算法进一步优化的贝叶斯算法[13]对模型截面层进行分区处理,利用凸多边形区域融合方法将截面层复杂图形分解为多个连续简单多边形,以此减少打印轨迹中的复杂图形数量[14]。由于人造肉原料挤出时的短暂流动性,且相比普通3D打印材料其直径较大,因此为避免打印路径中出现畸变以及拐角处的物料堆积现象,应尽量保证求解得到的图形为简单多边形,且其中每个内角尽可能大和均匀。
采用FarseerUnity物理引擎提取贝叶斯算法开源库,并结合Matlab进行相关实验验证。提取一种3D打印人造肉模型截面脂肪部分纹理进行分区,如图3所示。由结果分析可得,采用贝叶斯算法分区得到的复杂截面连续子分区均能满足要求,且由此为后续扫描轨迹优化打下基础。

图3 分区结果
2.2 子分区轮廓轨迹规划
2.2.1 轮廓起始点确定 在对模型截面层进行分区后可得到若干连续多边形子分区,随后需要对每个子分区分别进行轨迹规划,以此实现对各分区的打印成型。因此在打印前需对每个子分区轮廓确定一个运动起始点,要求各子分区仅有一个轮廓起始点且仅被经过一次,同时各分区在空间上运动连续,以此有效降低打印喷头运动的空行程距离,减少物料滴落,提高打印效率与模型成型质量[15-18]。
研究采用一种改进的近邻法确定各轮廓起始点[19],分析时设置各复杂截面层共分有m个简单多边形子分区,各分区可表示为L={L1,L2,L3,…,Lm},各多边形子分区共有n个顶点,则该顶点集合可表示为p={p1,p2,p3,…,pm},此时任意子分区的顶点集合可表示为pi={pi1,pi2,…,pikm},n=k1+k2+…+km。因此,确定各子分区轮廓起始点的实施步骤如下:
(1)根据子分区轮廓运动路径连续且起始点距离最小原则,可确定轮廓起始点的计算目标函数为:
(1)
式中:
s——子分区轮廓起始点,mm;
d——运动路径相邻两子分区起始点距离,mm;
x、y——起始点坐标。
(2)选取点集pi中的p11(0,0)作为该分区轮廓运动起始点,令s1=p11,根据式(1)可求得各子分区顺序起始点s1到各分区轮廓L的距离,随后将点p11从p中摘除。
(3)根据步骤(2)所求距离,可找出距离顶点s1最近的起始点pij,并将其摘除集合,同时令s2=pij。
(4)可根据式(1)依次求得顶点si到集合p中各个点的距离,并将所有计算结果比较得出距离顶点si最近的点,将其命名为sh。按照该思路依次遍历所有复杂截面子分区多边形轮廓顶点,可求得该子分区起始点集合L1={s1,s2,s3,…,sh}。
(5)比较集合L中各值,分别遍历其中各点并求任意两点间的距离,将其顺序排列,依次找出各距离最小值并对其求和,可表示为di=s1s2+s2s3+…+sn-1sn。
(6)遍历顶点集合p中各点,作为子分区轮廓运动起始点,并根据上述思路分别求解出所有起始点集合Li,并解出其中各起始点相对应最小距离di,可表示为集合D={d1,d2,d3,…,di}。
(7)比较集合D中各值大小,此时最小值di对应的起始点集合Li即为该复杂截面子分区轮廓运动轨迹最优起始点集合。
2.2.2 子分区轮廓路径规划 在确定各子分区轮廓运动起始点后,需要从起始点开始对分区轮廓进行稳定打印以此可以更好地包裹住内部填充,防止物料向外流动与坍塌。轮廓运动轨迹为从一起始点运动到终止点,可将该轨迹规划总结为旅行商问题(TSP),因此可采用蚁群算法对其进行求解。但由于传统蚁群算法求解初期的耗时长与盲目性大的缺点[20],进一步将遗传算法优秀的全局搜索特性融入蚁群算法,以得到子分区轮廓轨迹规划的最优解。
将已得到的各子分区轮廓最优起始点作为蚁群算法中运动蚁的待访点,进而对其进行迭代获得初步轨迹解集。将迭代后所得结果作为遗传算法的种群变量参数,并进行收敛求解出该复杂截面子分区轮廓运动轨迹最优解,以此优化运算精度,提高求解速度与效率。求解过程如图4所示。

图4 子分区轮廓轨迹规划流程

(2)
(3)
式中:
α——信息素影响因子;
β——启发函数影响因子。
在蚂蚁移动过程中,每移动一次就需统计增加其在所经过子分区轮廓路径上释放的信息素浓度,令该蚂蚁经过所有子分区轮廓后所产生的信息素总量记为Q,其所经过的有效路径(即从子分区轮廓i起始点到子分区轮廓j起始点)总路程长度记为Lw。为避免产生过多的冗余信息导致对启发信息与结果产生过多干扰因素,因此在对每只蚂蚁迭代过后都需要更新一次信息素浓度τij(t),其结果为:
(4)
式中:
ρ——信息素浓度降低影响因子。
考虑到蚂蚁的数量与实际影响因素,当蚂蚁所经过子分区轮廓路径无效时,此时更新的信息素浓度结果为:
τij(t+1)=(1-ρ)τij(t) (0<ρ<1)。
(5)
在对释放的所有蚂蚁都迭代完成后,可将该种群蚂蚁所经过的所有最优轨迹节点顺序路径归纳为集合C={c1,c2,c3,…,cm},此时该集合即为遗传算法的初始种群变量参数。
经蚁群算法迭代后,为满足遗传算法使用要求,需将该初始种群C进行遗传矩阵编码。此时可将该截面子分区表示为一个数组,令任两起始点之间的运动轨迹为一个数组元素,即遗传染色体,当求解完整个数组时,所有结果点之间的顺序连线即为所得出的一条运动轨迹。再次通过随机顺序遍历数组元素即可产生多条路径,并对其进行编号处理。
通过以上对数组元素的迭代处理便可形成一定数量的可行轨迹及其对应的一代染色体,进一步对该染色体群进行适应度筛选,通过适应度函数计算任一两子分区起始点间路径值,直到迭代完所有分区,并进一步对其结果进行比较。经比较该值越小则表示结果越好,即通过优胜劣汰对此一代染色体进行筛选所得对应的染色体品质越优异。此适应度函数可表示为:
(6)
式中:
S(x)——计算所有节点时所经过的轨迹路径总长度,mm。
进一步,对以上所筛选的结果采用交叉运算,即将交叉算子作用于二代染色体种群,以此根据交叉概率生成新的子代个体。然后以新的子代个体为基础按照变异概率执行变异运算随机产生变异个体,组成集合C',即新的子分区打印轨迹起始点集合,并在集合中不断随机选取两个未被重复选取的数值进行逆序排列以得到新的个体种群。
对上述所得出的最新种群以相同方法继续迭代得出新一轮子分区起始点集合以及各点间的距离值。最后,通过比较距离得出最小值,该值即为最终所需要的最短路径,即截面子分区轮廓打印运动轨迹最优解。
2.3 分区内部路径拐角优化处理
3D打印人造肉原料相比于普通3D打印材料挤出直径更大,因此对比众多3D打印扫描填充方法,zigzag扫描法因其实现简单并且与硬件适配度高,故采用zigzag法对截面分区轮廓内部进行打印填充最为合适。该人造肉脂肪组织原料在喷头内为非牛顿流体形态,故挤出时需要在平台上对其进行快速冷却才能够稳定成型,但由于热传递时间问题,物料在平台上仍会有极短暂时间处于流体状态,此时若仍采用传统zigzag扫描法,打印时在轨迹拐角处喷头会进行短时间内的加减速动作,将会产生物料堆积与坍塌现象,进而影响模型质量。
研究以zigzag扫描算法为基础进行适配性优化,核心思想为减少运动轨迹中的尖点,即减少喷头在拐角处的加减速与间断动作,优化方法如图5所示。当喷头完成直线扫描运动至拐角处时,将拐角处的尖角点改进为圆弧状以此作为两条直线路径的过渡区,喷头按照此圆弧轨迹就能够平滑运动进入下一条扫描线。当遇到极其相近的两条路径时,通过平台物料的短暂流动性即可自动对微小间隙进行填充。

图5 zigzag扫描优化方法
3 实验验证
建立具有复杂截面纹理的模型模拟人造肉脂肪组织部分,并对其进行3D打印轨迹规划及打印成型以此验证上述所提出的优化方法的可行性。
首先采用贝叶斯算法开源库对提取的截面进行分区,其纹理分区如图3所示,共有29个简单多边形轮廓,并在此基础上采用提出的经改进的近邻法确定各分区轮廓最优运动起始点,如图6所示。进一步,采用提出的轨迹规划算法对各分区起始点集进行迭代处理,确定并优化分区轮廓打印运动路径以得到最优运动轨迹。通过计算机对上述模型进行轮廓轨迹仿真,优化前后运动轨迹如图7所示,优化后轮廓打印运动路径长度由约112.340 mm降低至约91.996 mm,缩短约18%,此时最优运动顺序为S1-S2-S3-…-S24-S25。最后采用经改进的zigzag扫描法对分区轮廓内部进行填充,局部填充效果如图8所示。

图6 轮廓最优运动起始点集

图7 轮廓轨迹优化对比

图8 内部填充优化局部效果
使用研究建立的轨迹规划方法对比现有Cura与Prusa切片软件,对该模型单层截面进行轨迹规划与打印,其中喷头喷嘴直径为0.8 mm,设置打印基准速度为60 mm/s,其他参数均保持一致。如表1所示,在人造肉3D打印上研究所用轨迹规划方法喷头运动距离与打印时间相比于Prusa和Cura均显优势。

表1 模型单层截面打印数据对比表
4 结论
基于植物原料的人造肉脂肪组织3D打印提出一种运动轨迹优化算法,针对性地解决原料挤出直径较大与短暂流动性所造成的成品成型质量问题。采用贝叶斯算法对切片后的模型截面进行分割得到合理的若干简单多边形子分区,可有效减少打印时的空行程并为路径规划奠定基础;然后采用经改进的近邻法确定各截面子分区运动起始点;进一步将蚁群算法和遗传算法有效结合,用遗传算法良好的并行与搜索能力弥补蚁群算法计算耗时长与盲目性大的缺点,以此更好地对确定好起始点的子分区进行轮廓打印运动路径规划,提高打印效率;最后使用改进后的zigzag扫描法对子分区内部进行扫描填充,减少路径尖角与拐角,提高模型打印质量。
研究所提出的轨迹规划算法比较于传统切片软件Cura和Prusa中的算法,打印的模型单层截面运动路径长度分别缩减8.9%与11.3%,打印时间分别缩减15.4%与16.7%。

