另眼相看“圆的面积”

郜舒竹 李硕楠

【摘   要】我国小学数学课程中对于“圆的面积”的认识过程相对单一，而且存在逻辑相悖的现象，因此需要挖掘适合小学阶段学生认知规律的课程资源，丰富关于“圆的面积”的认知活动。通过历史文献考察发现，关于“圆的面积”认识的基本思路是将圆形与直边图形建立联系，除了目前教科书中常见的长方形，还有小学数学课程内容中熟知的正方形及三角形。这些直边图形都可以成为直观认识圆面积的课程资源，将此类内容融入数学课程教学中，可以让学生有机会经历“另眼相看”的认识过程，帮助他们积累对以后数学学习有意义的基本活动经验。

【关键词】圆的面积；纸草书；托里拆利；开普勒；亚伯拉罕

这里所说的“另眼相看”指得是用差异、多样的眼光看待同一对象。我国小学数学课程中对于“圆的面积”的认识过程相对单一，而且存在逻辑相悖的现象。因此需要挖掘适合小学阶段学生认知规律的课程资源，让学生有更多的机会经历“另眼相看”圆的面积的认识过程，在不违背逻辑的基础上，用更加丰富的认知活动直观认识圆的面积。

一、教科书中的“逻辑相悖”

我國小学数学教科书中关于“圆的面积”的认识过程，采用的是15～16世纪意大利艺术家、科学家达芬奇（Leonardo da Vinci，1452—1519）发明的直观方法，类似方法也出现于日本佐藤茂春（英译：Sato Moshun）1698年出版的《算法天元指南》第九卷中。将圆形与长方形建立联系，利用“长方形面积=长[×]宽”得到“圆的面积=[πr2]”。［1］［2］具体做法是将圆形等分为若干小扇形，剪开后将小扇形重组为形状近似于长方形的图形（以下简称“准长方形”）（如图1）。

2022年8月出版的人教版教科书六年级上册第65页表述的推理过程为：“分的份数越多，每一份就越小，拼成的图形就越接近于一个长方形。”长方形的长“近似”于圆周长的一半[πr]，宽“近似”于圆半径[r]；因为“长方形的面积=长[×]宽”，所以“圆的面积=[πr×r=πr2]”。

这一过程是从外观的“接近”，推理出长与宽长度的“近似”；从长与宽长度的“近似”，推理出面积的“相等”，在一个并非是长方形的准长方形上使用长方形的面积公式。实际教学中发现，学生对这样的推理过程难以接受，产生的问题是：无论多么接近，也不是真正的长方形。为什么能够在不是长方形的图形上使用长方形面积公式？

产生这样的问题是合情合理的，外观上的“接近”并不能直接推理出长度的“近似”；长度的“近似”也不能直接推理出面积的“相等”。举例来看，任意三角形一个具有普遍性的性质是“两边之和大于第三边”。对于直角三角形，两条直角边长度之和，应当大于斜边的长度，因此对于图2中的大直角三角形（实线）应当有[a+b>c]。

图2中的三个图形，是将一个大直角三角形的斜边等分为若干份，以每一份为斜边作小直角三角形，不难看出每个图中所有小直角三角形直角边（虚线）之和，等于大直角三角形的直角边之和“[a+b]”。

直观看这些小三角形，随着份数的增多，越来越“接近”大三角形的斜边，但无论多么接近，这些小三角形直角边的总和都是“[a+b]”，因此这样的“接近”仅仅是视觉上外观的接近，不能推理出与斜边长度“[c]”的近似。这说明外观的“接近”与数量的“近似”并不具备必然的因果关系，“因为接近，所以近似”的推理未必成立，因此可以说教科书中关于圆面积的推理过程，混淆了外观的“接近”与数量的“近似”二者之间的关系。

另外，教科书中用长方形的面积公式推理出圆的面积公式的前提，是长方形的长和宽分别“近似”于圆周长的一半[πr]和半径[r]，通过近似值的乘法运算得到圆面积的准确值，这样“因为近似，所以相等”的逻辑也是说不通的［3］。凡与此逻辑相悖的现象都是数学课程与教学研究需要解决的问题。

事实上，从逻辑上严格推导并证明圆的面积公式，无法回避微积分中极限的概念，这在小学乃至初中阶段是行不通的。因此需要探讨的问题是：如何在不违背逻辑的前提下直观认识圆的面积公式？这就需要对圆的面积公式的发生与发展的历史进行考察，从中可以发现一些具有借鉴意义的方法。

二、圆与正方形

关于圆的面积测量最为久远的记载是在距今约3700年，公元前1650年左右古埃及数学著作《莱因德纸草书》（Rhind Papyrus）中，这本书是目前发现的最古老的数学著作之一。书中共有87个数学问题，48～55题都与平面图形的面积相关，第50题记载的圆的面积的求法是“直径的九分之八的平方”［4］。如果一个圆的直径是[d]，那么这个圆的面积就近似于[（8/9×d）2]，这一公式与今天熟知的[πr2]不同，是用有理数表达圆的面积近似求法，相当于将无理数[π]取近似值为“[π≈3.16]”。下面对得到这一结果的过程进行分析。

整个过程的基本思路是将圆形与正方形以及六边形建立联系，首先作出圆形的外切正方形，将正方形每条边三等分，连接分点作出一个六边形。想象将大正方形顶点处的四个小三角形去除，直观看所剩下的六边形面积与圆的面积就很接近，这个六边形面积实际就是大正方形面积减去四个小阴影三角形的差。具体步骤如图3。

从图3第四步不难发现，去除的四个小三角形面积之和是大正方形面积的[418=29]。如果圆的半径为[r]，那么六边形面积为：[（1-29）×4r2=289r2]。如果用字母[d]表示圆的直径，那么六边形面积可以表示为“[79d2]”，接下来运用分数基本性质做如下的转换：

这样就得到圆的面积简单易行的近似算法“直径的九分之八的平方”。如果一个圆的直径为9厘米，立刻可以知道该圆的面积近似于64平方厘米，与“[πr2]”计算的结果“[3.14×4.52≈63.59]”非常接近。在这种情况下，圆周率的近似值为“[π≈][（89）]2×22=[25681]”，化为小数约等于[3.16]［5］。

这一结论具有实用的特点，如果已知一个圆的直径，只需要将其略微减小而后平方，就可以得到圆面积的近似值。整个过程的基本思路是通过减少正方形与圆形之间的差异，利用正方形的面积近似求出圆的面积。如果这样的“减少”到达“穷竭”，“近似”就成为“相等”，因此类似这样的方法叫作“穷竭法（Exhaustion）”，是历史上解决曲线图形求积问题的经典方法，其中已经蕴含了“趋近于（Approach）”的极限思想。［6］

三、圆与三角形

古希腊伟大的数学家、科学家、发明家阿基米德（Archimedes，公元前287—公元前212）所著《圆的测量》中的第一个命题为：“任意圆的面积与直角边分别为圆周长和圆半径的直角三角形面积相等。”［7］这一命题是将圆的面积与熟知的三角形面积建立联系，如果已知圆半径和周长，就可以求出圆的面积。

阿基米德使用穷竭法证明的过程相对复杂，因此后人探索并发明出一些能够直观看出的方法，其中最著名的叫作“不可分量法”。“不可分量（Indivisible）”的概念源于对连续量的认识，把几何中的“线、面、体”分别视为是低一维的“点、线、面”构成，认为“积点成线、积线成面、积面成体”，或“点动成线、线动成面、面动成体”［8］。

在欧洲最早系统使用不可分量法研究几何“求积”①问题的，是17世纪意大利数学家卡瓦列里（Cavalieri Francesco Bonaventura，1598—1647）。他用隐喻的方式解释不可分量：制衣过程中需要用线织布，因此二维的“布”是一维的“线”构成的，“线”就成为“布”的不可分量；如果把一本书视为是三维的立体图形，把其中的一“页”纸看作二维的图形，那么三维的“书”就是二维的“页”构成的，“页”就成为构成“书”的不可分量。［9］类似的方法我国南北朝时期的数学家祖暅（456—536）就已经发现，并应用于求积问题［10］。应用不可分量法比较几何图形的面积或体积，主要依据两个判断：

●   不可分量一一对应且相等，则面积（或体积）相等；

●   不可分量一一对应，則不可分量之比等于面积（或体积）之比。［11］

比如在小学阶段，我们熟知的“等底等高的三角形面积相等”，用不可分量法直观看就是非常明显的（如图4）。

卡瓦列里的好友，17世纪意大利以物理学成就著称的托里拆利（Evangelista Torricelli，1608—1647），［12］于1644年出版的《几何概览》（Opera Geometrica）中，就是用不可分量法直观证明阿基米德的命题。［13］具体过程如下。

作圆[O]和对应的直角三角形[AOA]'，三角形底边[AA]' 长度等于圆周长，高等于圆半径[AO]。以[O]点为圆心在内部任意作小同心圆（虚线），想象圆[O]是无数个这样的同心圆构成，把同心圆周长视为圆[O]面积的不可分量（如图5）。将每一个同心圆沿着半径剪开拉直（图5中[BB]'），转化为三角形[AOA]' 的不可分量，使圆与三角形的不可分量建立了一一对应的关系，并且长度相等，因此圆[O]与三角形[AOA]' 面积相等，这样就可以用三角形面积求出圆[O]的面积为：[12×2πr×r=πr2]。这一方法可以用动态的过程演示出来（如图6）。

与此类似的还有11～12世纪西班牙裔犹太数学家亚伯拉罕（Rabbi Abraham bar Hiyya Hanasi，1065—1136）发明的方法：将圆沿半径剪开后，以对称的方式两侧同时展开成为等腰三角形［14］（如图7）。

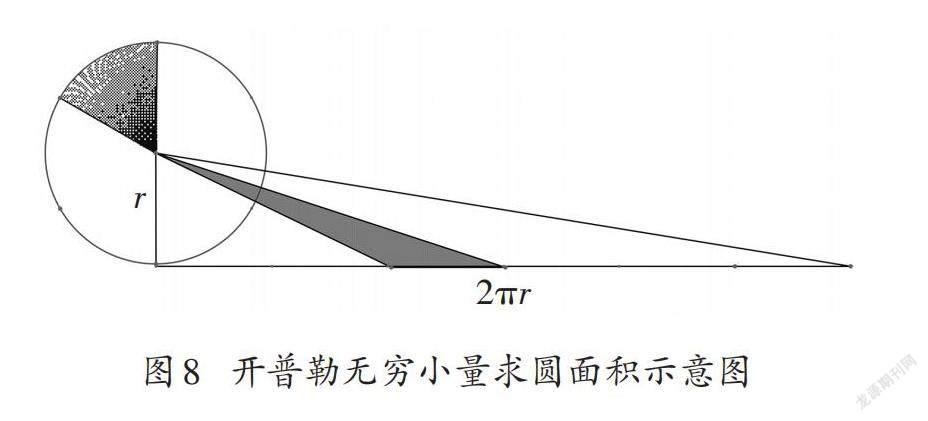
与托里拆利同时代的德国天文学家、数学家开普勒（Johannes Kepler，1571—1630），也用类似的方法研究圆的面积。将圆等分为若干小扇形，沿半径剪开并拉直，展开为直角三角形后，直角三角形的两条直角边长度分别等于圆半径和圆周长。想象小扇形拉直后成为大三角形中的小三角形（如图8）。圆内的小扇形与大三角形中的小三角形一一对应并且面积相等，因此圆与大三角形面积相等。［15］

开普勒看待不可分量的眼光与卡瓦列里和托里拆利略有不同，是将不可分量看成与圆形和三角形同样的二维平面图形，随着份数的增多，圆内的小扇形和三角形中的小三角形无限缩小，是能够小于任意有限量的“无穷小量（Infinitesimal）”，圆与三角形的面积分别由这些面积相等的无穷小量构成，因此圆与三角形的面积相等。这种无穷小量的思想日后逐渐发展成为极限理论的逻辑基础。

以上方法依赖的是不可分量或无穷小量之间一一对应及量的相等关系，通过不可分量或无穷小量的关系，可以直观看出圆与三角形面积之间的相等关系。这样的方法并非是严格的证明，但对于通过直观感知，进而实现数学发现是有效的。将圆形沿着半径剪开、拉直为直角三角形或等腰三角形，得到的是真正的三角形，这时利用三角形面积的求法得到圆面积，可以实现在不违背逻辑的前提下直观认识圆的面积的目的。不仅如此，类似的方法还可以迁移到中学数学课程中球的体积的认识。

四、“另眼相看”的威力

数学课程与教学承载着培育“数学的眼光、数学的思维、数学的语言”的使命。同样的圆，可以转化为长方形，也可以转化为正方形或三角形；同样圆的面积公式，可以表达为“[圆周率×半径2]”，也可以表达为“[（89直径）2]”或“[12×周长×半径]”。

这样的“另眼相看”体现的是“眼光的差异性、思维的灵活性、语言的丰富性”，是在“同中求异”的认知过程中发展思维的灵活性和发散性。除此之外，这样的经历还可以成为将来数学学习的经验，将今天经历的过程与方法迁移到今后相关内容的学习过程中，实现不同课程内容思维方式的关联。

如前所述，将圆形转化为三角形的方法，是将平面图形的圆周转化为三角形的底边，圆的半径转化为三角形的高，用三角形的面积公式得到圆的面积公式。类似的方式可以迁移到中学立体几何中球与圆锥体积之间关系的认识，用圆锥体积公式得到球的体积公式。如果一个球的半径为[r]，那么表面积为[4πr2]（如图9）。

如果把圆周视为是平面图形圆的边界，那么立体图形球的边界就是表面，因此圆的周长与球的表面积都表示“界的大小”；类似于此，平面上三角形的底边长度类似于立体图形圆锥的底面积，都表示“底的大小”。这时阿基米德关于圆面积的命题，就可以类比为球的体积的命题：“任意球的体积，与底面积和高分别等于球表面积[4πr2]和半径[r]的圆锥体积相等。”也就是说，利用熟知的圆锥体积公式“[13×底面积×高]”，就可以得到球的体积公式：[13×4πr2×r=43πr3]。球与圆的类比关系可以用表1清晰地呈现出来。

平面图形的“圆与三角形”与立体图形的“球与圆锥”，是维度不同的几何对象，而且位于不同的学段，但其中内在的联系具有高度的一致性，小学阶段对圆的面积的“另眼相看”，可以成为今后数学学习认知方式的基础。让学生有机会经历不同过程，对他们以后的学习有积极的意义。积累普遍适用的基本活动经验，应当成为小学数学课程与教学的重要目标。

课程与教学的目的不仅是“知道”，更要强调“经历”，在经历中逐步实现“眼光的差异性、思维的多元性、表达的丰富性”。这就要求教科书编修及实际教学秉承守正创新的理念，避免故步自封，开发出更加丰富并且适合学生发展核心素养的课程资源和学习活动，让学生有更多的机会经历“另眼相看”的过程，让素养导向的课程与教学落在实处。

参考文献：

［1］SMITH D E，MIKAMI Y. A history of Japanese mathematics ［M］. Chicago：Open Court Publishing Company，1914：130–132.

［2］BECKMANN P. A History of PI［M］. New York：St. Martin' s Press，1976：19.

［3］郜舒竹.“圆面积公式”的误教与修正［J］.教学月刊·小学版（数学），2018（4）：10-12.

［4］SMEUR A J E M. On the Value Equivalent to π in Ancient Mathematical Texts. A New Interpretation［J］. Archive for History of Exact Sciences，1970，6（4）：249-270.

［5］SEIDENBERG A. On the Area of a Semi-Circle［J］. Archive for History of Exact Sciences， 1972，9（3）：171-211.

［6］张奠宙.话说“无限”［J］.数学通报，2006（10）：1-4.

［7］HEATH T L. The Works of Archimedes［M］. Cambridge： Cambridge University Press，1897： 91–98.

［8］EVANS M G. Aristotle，Newton，and the Theory of Continuous Magnitude［J］. Journal of the History of Ideas，1955，16（4）：548-557.

［9］EDWARDS  C H J. The Historical Development of the Calculus［M］. New York：Springer-Verlag，1979：104.

［10］李大华.祖暅原理的探索性内涵［J］.数学通报，2006（1）：27-28.

［11］ANDERSEN K. Cavalieris Method of Indivisibles［J］. Archive for History of Exact Sciences，1985，31（4）：291-367.

［12］江舫.托里拆利（纪念托里拆利诞辰350周年）［J］.物理通报，1958（10）：584-586.

［13］ROBINSON P J. Evangelista Torricelli［J］.The Mathematical Gazette，1994，78（481）：37-47.

［14］EPSTEIN S，HOCHBERG M. A Talmudic Approach to the Area of a Circle［J］. Mathematics Magazine，1977，50（4）：210.

［15］BERO P. Calculations in the Style of Kepler［J］. For the Learning of Mathematics， 1993，13（3）：27-30.

（1.首都师范大学初等教育学院 2.首都师范大學教育学院）